MODELLING THE INTERACTION OF THRUSTERS WITH THE SOIL USING THE DISCRETE ELEMENT METHOD IN ROCKY DEM

На современном этапе развития механизации сельскохозяйственного производства наиболее существенным резервом является повышение продуктивности полей за счет своевременного выполнения работ на базе высокопроизводительной техники и снижения воздействия их движителей на почву

Совершенствование движителей является основным способом снижения вредного воздействия их на почву, а также улучшения тягово-сцепных показателей. Вопросы взаимодействия движителей с почвой и обоснования рациональных параметров освещены в работах А.С. Антонова, Е.Д. Львова, Н.А. Забавникова, М.Г. Беккера, Дж. Вонга, М.И. Медведева, Е.М. Харитончика, В.В. Гуськова, А.В. Васильева, Е.Н. Докучаевой, О.Л. Уткин-Любовцова, М.И. Ляско, И.П. Ксеневича, В.А. Скотникова, Б.Н. Пинигина, Б.М. Куликова, Д.И. Золотаревской и многих других ученых.

Определение способов радикального снижения уплотнения почвы МТА возможно на основе углубленного изучения взаимодействия движителей с почвой, в результате которого можно разработать математические модели процессов и рекомендации для решения поставленных задач.

При теоретическом обосновании параметров движителей тракторов и сельскохозяйственной техники используются различные методы моделирования, которые можно классифицировать по методам численной реализации и применяемых компьютерных программ.

Целью работы является анализ моделей, используемых для моделирования взаимодействия движителей с почвой методом дискретных элементов и разработка методики моделирования взаимодействия колеса с почвой в программе Rocky DEM.

Технический обзор литературы и информации по контактным моделям. Программа Rocky DEM для моделирования динамики сыпучих сред со сложной геометрией частиц методом дискретных элементов (DEM). Rocky DEM отличается аналогичных программных продуктов следующими функциями: несферические формы частиц, мульти-GPU вычисления, расчет разрушения частиц без потери массы или объема и визуализация поверхностного износа. В результате интеграции Rocky DEM и Ansys Workbench расчет и моделирование взаимодействия частиц можно выполнять с учетом аспектов механики деформируемого твердого тела, вычислительной гидрогазодинамики и теплообмена. Также при использовании Ansys Workbench можно выполнять многофазные эксперименты.

В зависимости от методов численной реализации моделей взаимодействия движителей с почвой их можно подразделить на три основных вида: модели с использованием метода вычислительной гидродинамики (CFD-метод), модели с использованием метода конечных элементов (FEM-метод) и модели с использованием метода дискретных элементов (DEM-МДЭ)

В настоящее время перспективным для моделирования взаимодействия движителей с почвой является метод дискретных элементов. МДЭ – это численный метод, предназначенный для расчёта движения большого количества частиц, таких как молекулы, песчинки, гравий, галька и прочих гранулированных сред. Метод был первоначально применён Cundall в 1971 году для решения задач механики горных пород

В МДЭ дискретный материал образуется из отдельных N упругих частиц сферической формы радиусом Ri. Движение каждой i-го элемента (частицы) определяется координатами центра его тяжести xi и углом поворота θi вокруг центра тяжести как целого элемента

Система уравнений движения для каждой частицы при МДЭ

(1)

где, t – время, с; mi – масса частицы, кг; Ii – момент инерции, кг·м2.

Вектор Fi определяются как сумма сил, действующих на контактах i-й и j-й частиц (включая силу тяжести):

(2)

Вектор Mi возникает как момент сил Fij относительно центра i-й частицы:

(3)

Поверхностные силы Fijсостоят из сил трения Ft,ij и отталкивания Fn,ij. Для их определения используются различные контактные модели соударения. Сила отталкивания возникает между частицами при условии δij > 0 (рис. 1) и направлена по нормали nij в направлении центра i-й частицы (рис. 2). Для ее определения выберем вязкоупругою модель соударения

(4)

Fn,ije – упругая составляющая, Н; Fn,ijv – вязкая составляющая, Н.

Упругая часть силы в соответствии Дж. Герцу

(5)

где νi – коэффициент Пуассона, Ei – модуль упругости частицы, Па, δij – величина перекрытия частиц, м.

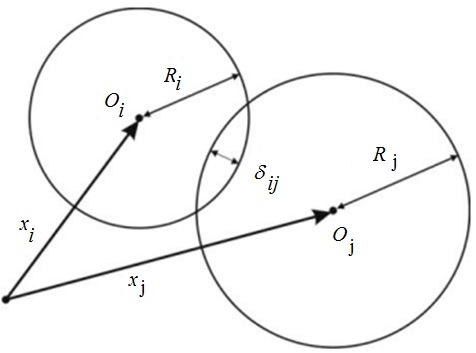
Рисунок 1 - Геометрия модели контактного взаимодействия частиц

DOI:10.23670/IRJ.2023.131.29.1

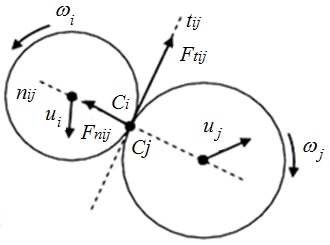
Рисунок 2 - Силы, действующие при контактном взаимодействии частиц

DOI:10.23670/IRJ.2023.131.29.2

Вязкая составляющая силы отталкивания определяется:

(6)

где Mij – приведенная масса частиц, кг; un,ij – проекция относительной скорости точки соударения на ось nij, м/с; γn – коэффициент демпфирования, оказывающий основное влияние на коэффициент восстановления скорости после удара

Сила трения Ft,ijнаправлена против движения i-й частицы относительно j-й, а ее величина определяется:

(7)

где ut,ij – проекция скорости точки контакта Ci относительно скорости точки Cj на ось tij, м/с; φt – угол контактного трения между частицами, рад.

Следовательно, система дифференциальных уравнений второго порядка (1) относительно неизвестных xi, θj полностью определяет (3)-(7) движение и соударение совокупности моделируемых частиц.

На основе анализа существующих моделей контакта дискретных элементов, мы пришли к выводу, что для моделирования почвенной среды как вязко-упруго-пластического деформируемого тела наиболее подходящими являются модели контакта Герца-Миндлина: – модель и теория скользящего контакта Герца-Миндлина (без проскальзывания); – модель Герца-Миндлина с адгезией связывающих частиц; – модель когезионного контакта Герца-МиндлинаJKR (Johnson-Kendall-Roberts).

Модель когезионного контакта Герца-Миндлина JKR (Johnson-KendallRoberts) учитывает влияние сил Ван-дер-Ваальса в зоне контакта и позволяет моделировать прочно адгезивные системы (сухие или влажные материалы). В этой модели реализация нормальной упругой контактной силы основана на теории Джонсона-Кендалла-Робертса, изложенной в (Johnson, KendalandRoberts 1971).

(8)

(9)

(10)

где E* – эквивалентный модуль Юнга, Па; R* - эквивалентный радиус, м; δn – нормальное перекрытие, м; Ea, va, Ra и Eb, vb и Rb – модуль Юнга, Па; коэффициент Пуассона и радиус контактных сфер, м.

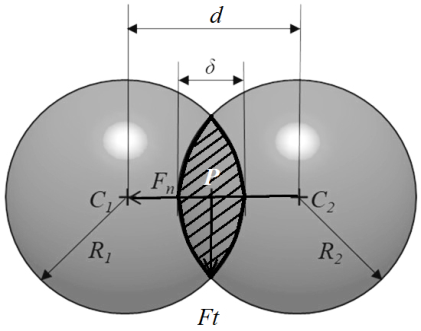
Рисунок 3 - Расчетная схема взаимодействия частиц по модели Герца-Миндлина JKR

DOI:10.23670/IRJ.2023.131.29.4

Касательная сила Ft между частицами определяется:

(11)

где

(12)

где St – жесткость на сдвиг, Па; δt – тангенциальное перекрытие, м; G* – эквивалентный модуль сдвига, Па.

Нормальное перекрытие двух контактирующих частиц:

(13)

где

(14)

xA,i и xB,i – координаты центров A и B единиц частицы, соответственно, м; d – расстояние между центрами двух частиц, м.

Коэффициенты нормальной kn и тангенциальной ks жесткости двух контактирующих частиц определяются:

(15)

Контактная жесткость между двумя частицами моделируется как набор упругих пружин с постоянной нормалью и жесткостью на сдвиг в точке контакта. Параллельная связь заменяет сцепление между комками почвы.

В современных компьютерных программах, реализующих данный метод, хотя и заложены необходимый математический аппарат и алгоритм построения (рис. 4) и реализации моделей, однако исследователю для получения объективных и адекватных результатов необходимо правильно подобрать основные геометрические параметры частиц и физико-механические параметры, входящие в математические уравнения используемой модели.

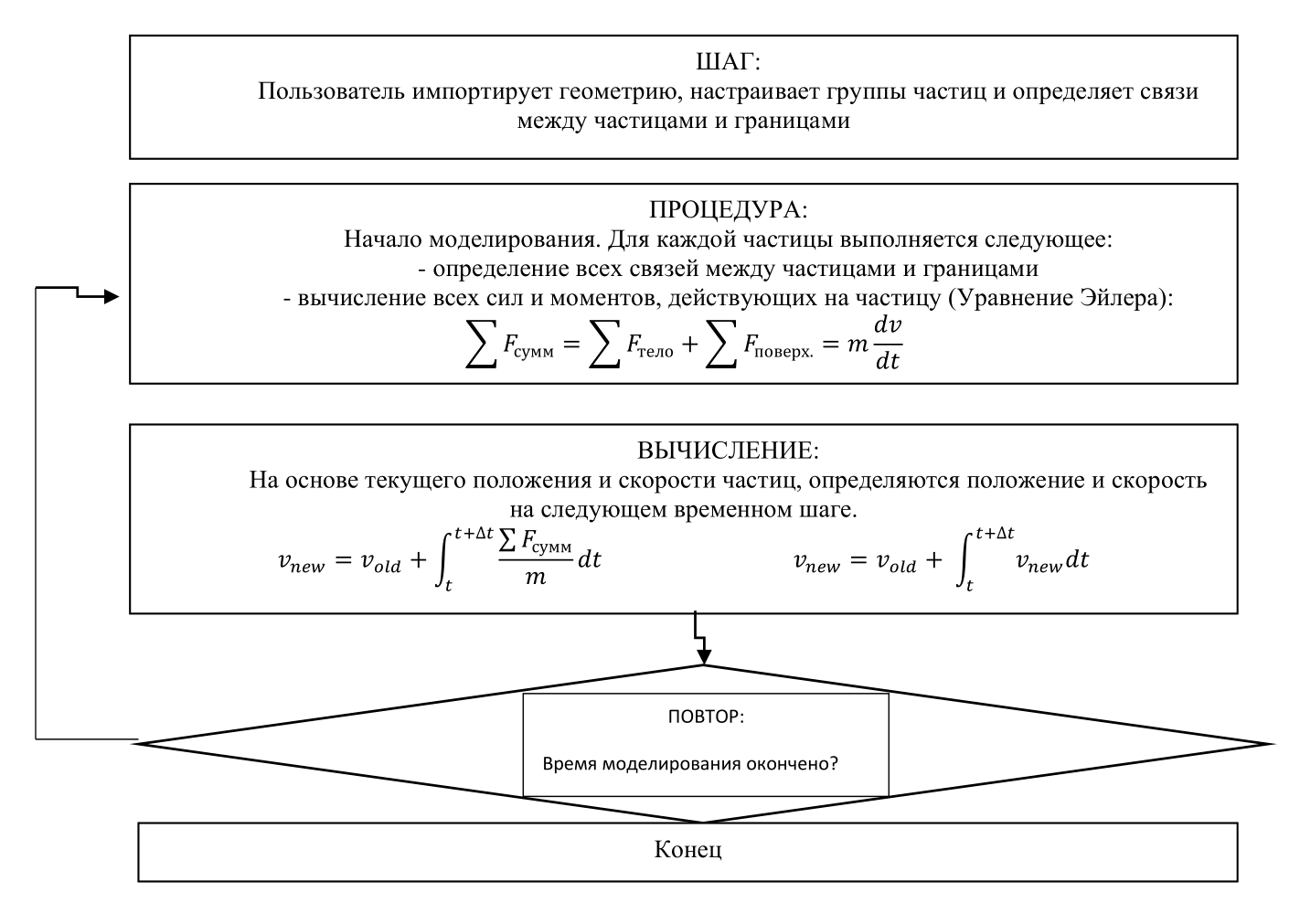
Рисунок 4 - Алгоритм численной реализации модели почвенной среды в программе Rocky DEM

DOI:10.23670/IRJ.2023.131.29.5

При использовании контактной модели Герца-Миндлина основными физико-механическими параметрами, описывающими реологическое поведение моделируемой среды, являются коэффициент Пуассона, коэффициенты статического и динамического трения, модуля Юнга, поверхностная энергия, диаметр и форма моделируемых дискретных элементов (рис. 5).

Однако до сих пор не существует стандартизированной методологии для определения подходящих входных параметров для конкретного материала или процесса. Это происходит из-за того, что математические характеристики контактных моделей и входных данных моделирования различаются в зависимости от кода матрицы высот. В дополнение к этому в любом случае модель почвенной среды на основе DEM является лишь приближением реальной почвы, как и в случае со всеми типами моделей сред. К тому же почва отличается от многих исследуемых материалов анизотропностью физико-механических свойств, тем более эти свойства изменяются как по времени, так и в пространстве. Поэтому с вычислительной точки зрения просто невозможно создать модель полностью соответствующий реальному объекту. Из-за этих ограничений входные данные для моделирования DEM необходимо откалибровать по реальным, физическим данным испытаний, чтобы получить реальный результат.

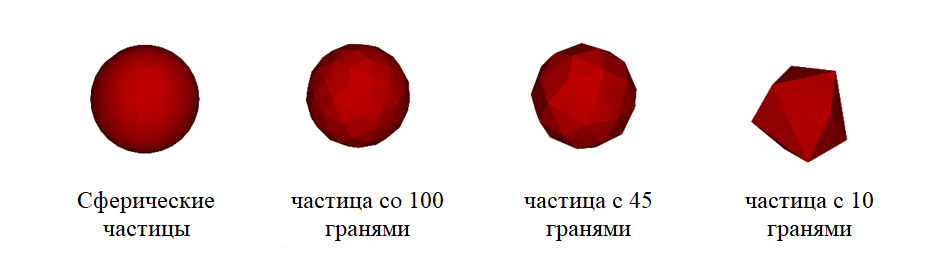
Рисунок 5 - Модельное представление форм частиц в программе Rocky DEM

DOI:10.23670/IRJ.2023.131.29.6

Калибровка параметров моделей контакта на первоначальном этапе производилась по срезу на сдвиговом приборе, по углу естественному откоса. В последующем, перешли к сопоставлению результатов моделирования и экспериментов.

Нами разработана модель взаимодействия колесных движителей с почвой на основе метода дискретных элементов.

Численная реализация разработанной модели почвенной среды производилась в лицензионной компьютерной программе Rocky DEM. Поэтапная реализация компьютерной модели включает в себя следующие шаги (рис. 6):

- проектирование трехмерных твердотельных моделей колеса тракторов и сельскохозяйственной техники и почвенного канала в системе проектирования КОМПАС 3D;

- импорт геометрий трехмерных твердотельных моделей, настройка группы частиц и определение связи между частицами и границами;

- процедура расчета при которой для каждой частицы определяются все связей между частицами и границами, вычисляются все силы и моменты, действующие на частицы;

- процесс вычисления при котором на основе текущего положения и скорости частицы, определяется скорость и положение на следующем временном шаге;

- окончание расчета и анализ полученных результатов.

В результате моделирования можно получить действительную картину взаимодействия движителей с почвой, провести агротехническую и энергетическую оценку по силовым характеристикам процесса взаимодействия, по перемещению и перемешиванию почвенных частиц и уплотнению почвы.

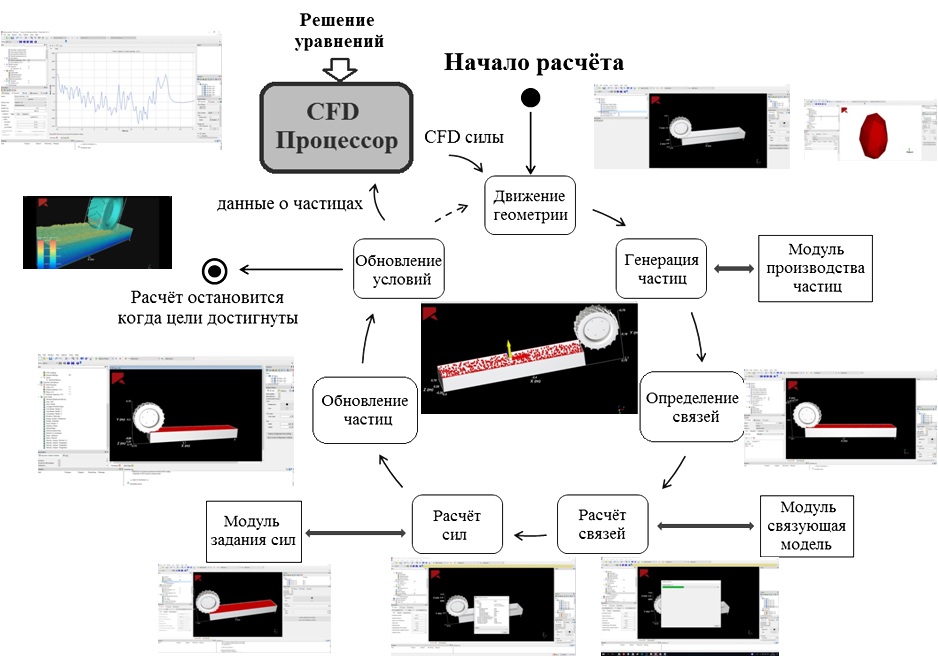
Рисунок 6 - Реализация модели взаимодействия колеса с почвой в программе Rocky DEM

DOI:10.23670/IRJ.2023.131.29.7

Необходимо отметить, что расчет технологических процессов при помощи метода DEM подразумевает моделирование большого количества частиц, часто от миллиона и более, что безусловно требует соответствующей производительности вычислительных ресурсов.

Например, время расчета задачи при моделировании движения 1 миллиона сферических частиц по конвейерной линии на компьютере с 4-мя ядрами составляет примерно 11 часов, а для подобной задачи с несферическими частицами более 48 часов.

На рисунке 7 показаны результаты процесса взаимодействия шина-грунт, где наглядно видны процессы уплотнения почвы и образования колеи после прохода колеса, а также прилипание почвенных комков. Объектом исследований является колесо с шиной 23,1 R26 колесного трактора Т-150К, тип почвы – суглинок. В таблицах 2, 3 представлены параметры почвенной среды и основные параметры шины.

На рисунке 8 показан фрагмент графика изменения силы сопротивления качению колеса и в таблице 4 представлены результаты вычислений следующих показателей: силы сопротивления качению колеса, мощности потребляемой колесом и плотности почвы по центру колеи колеса на глубине 18 см.

Расчеты численного моделирования показали, что сила сопротивления качению колеса при движении изменялась в интервале 2458,3…11408,05 Н, со средним значением 4408,36 Н. Мощность, потребляемая колесом, находился в пределах от 7758,64 до 18768,83 Вт со среднем значением 16176,69 Вт. Максимальное значение плотности почвы по следу на глубине 18 см увеличилось до 1502,7 кг/м3. Среднее значение плотности составило 1372 кг/м3, что привело к ее увеличению по следу колеса на 14% по сравнению с равновесной плотностью равной 1200 кг/м3.

На основе результатов исследования следует, что в дальнейших исследованиях необходимо провести обоснование выбора моделей контакта в зависимости от типа почвы, а также параметров моделируемой дискретной почвенной среды – коэффициента Пуассона, коэффициента статического и динамического трения, модуля Юнга, адгезионных и когезионных свойств и др. и сопоставить эти параметры с физико-механическими свойствами различных типов почв в зависимости от их влажности и плотности.

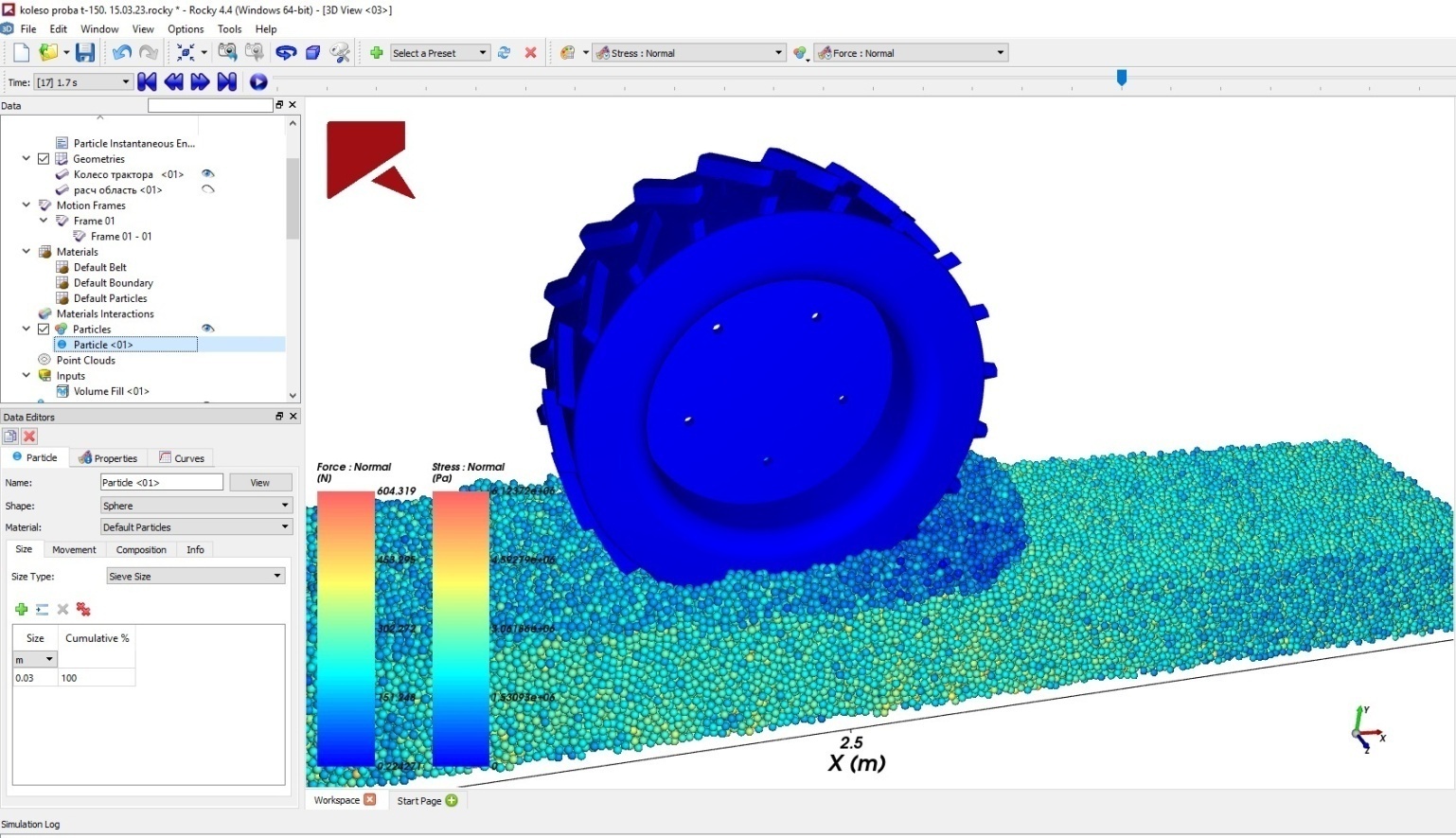
Рисунок 7 - Визуализация модели взаимодействия колеса с почвой

DOI:10.23670/IRJ.2023.131.29.10

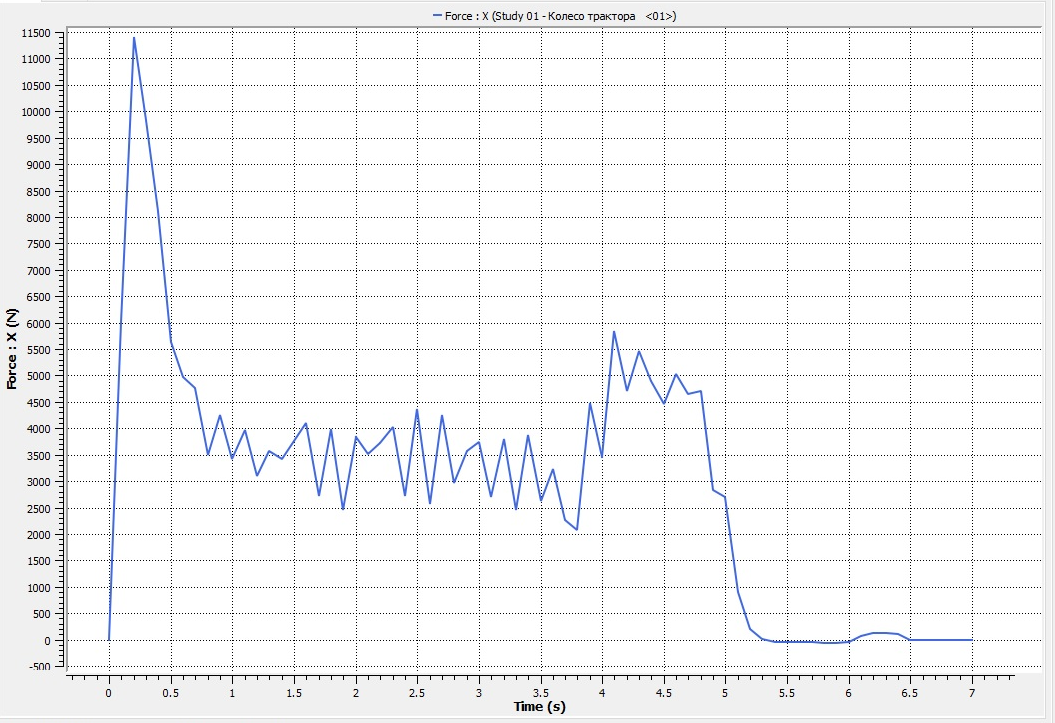
Рисунок 8 - Изменение силы сопротивления качению колеса

DOI:10.23670/IRJ.2023.131.29.11

Таким образом, почвенные частицы обладают когезионными и адгезионными свойствами и почва является упруго-вязко-пластичной средой для моделирования взаимодействия движителей с почвой наиболее подходящим является модель контакта Герца-Миндлина.

Разработана модель взаимодействия колеса с почвой на основе метода дискретных элементов в программе Rocky DEM.

Полученные результаты можно использовать при энергетической и агротехнической оценке и оптимизации конструктивно-технологических параметров движителей тракторов и сельскохозяйственной техники. Предложенная методика позволяет повысить разработки новых конструкций движителей и постановки их на производство в предприятиях тракторного и сельскохозяйственного машиностроения.

В последующем модель почвенной среды на основе метода дискретных элементов должна учитывать неровности рельефа поля, анизотропность свойств почвы и динамический характер рабочих процессов и показывать процессы буксования и уплотнения.