AN EVALUATION OF LONGITUDINAL STABILITY OF THE QUANTUM CAR BASED ON AERODYNAMIC PARAMETERS OF THE ANALOGUE ONE

На базе идей извлечения энергии из физического вакуума (ФВ)

Основная особенность ТС с КД заключается в том, что КД по схеме воздействия на экипаж подобен реактивному двигателю (РД). Однако в отличие от РД (где траст создается как реакция на импульс отбрасываемой массы газов, получая эту массу в качестве опоры), КД создает траст за счет деформации поля ФВ, обеспечивая опору трасту во внешней части задействованного фрагмента поля

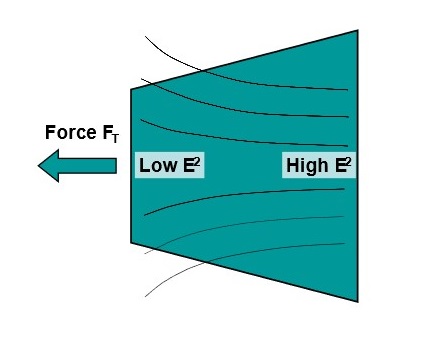
Рисунок 1 - Градиент плотности поля E2 в конусном резонаторе, приводящий к возникновению траста FT

DOI:10.23670/IRJ.2023.136.24.1

Установка КД на ТС позволит изъять трансмиссию из конструкции ТС, поскольку траст способен непосредственно двигать экипаж. Совокупность колес экипажа теряет функцию движителя, они остаются опорными. Вывешенный над опорной поверхностью (ОП) траст меняет схему сил и моментов, используемую для автомобиля. Точки возникновения сил тяги в пятнах контакта ведущих колес традиционных автомобилей переносятся в точки приложения вектора тяги КД к корпусу ТС. КД, по сути, становится и движителем

[3]

,

[15]

. Наземное ТС с КД названо автором квантомобилем

[13]

.

При возможности переводить вектор траста в наклонное положение можно за счет вертикальной составляющей этого вектора осуществлять прижим экипажа к ОП, либо его вывешивание. Это также видоизменит схему сил и моментов традиционных наземных ТС

Разница в величинах вертикальных нагрузок на опорные колеса экипажа, с точки зрения сохранения продольной устойчивости, для автомобиля в большинстве случаев имеет второстепенное значение – поскольку при движении автомобиля названые нагрузки отражаются встречными реакциями твердой ОП, что обеспечивает продольную устойчивость. В случае квантомобиля, однако, во-первых, из-за отсутствия ограничений по сцеплению колес с ОП возможна реализация тяговой силы, превосходящей допустимую для автомобиля. Во-вторых, траст, вывешенный над ОП, формирует составляющую опрокидывающего момента, отсутствующую в автомобильном варианте кинематической схемы. В-третьих, в отсутствие твердой опоры вывешенный (даже частично) квантомобиль получит склонность к вращательному движению в плоскости тангажа

Вывешивание (лифт) может привести к реализации режимов летательного аппарата. Реализация прижимающей силы (антилифт) при движении ТС в воде может позволить даже реализацию режима подводной лодки. Это привело к идее всесредного мультимодального квантомобиля (ВМК)

В формирование суммарного опрокидывающего момента (питч-момента) вносят вклад три группы сил: сопротивления качению колес, силы инерции и силы аэродинамического воздействия

2.1 Цель и задачи исследования

Обобщая изложенное, целью исследования поставили моделирование и оценку продольной устойчивости квантомобиля на базе материалов аэродинамических испытаний автомобиля-аналога.

Устранение трансмиссии, перенос движительных функций с опорных колес на КД, появление возможности осуществлять лифт и антилифт наземного ТС – всё это, в отсутствие теоретических основ движения квантомобиля и эмпирических данных, вызывает необходимость использовать подход с опорой на программное имитационное моделирование (ПИМ).

Задачами по достижению цели являются:

1) формирование математической модели (ММ) продольного движения квантомобиля (МПДК) под поставленную цель;

2) построение Simulink-модели функционирования наземного ТС с охватом имитации стендовых аэродинамических испытаний и дорожного движения, с отработкой интерфейса взаимодействия с моделью и вывода данных;

3) на базе Simulink-модели проведение ПИМ, покрывающего некоторое множество вариантов испытаний наземного ТС – с целью формирования методики привлечения существующих материалов испытаний автомобилей-аналогов для прогнозирования устойчивости квантомобилей;

4) обсуждение и обобщение результатов расчетов с получением оценок продольной устойчивости квантомобиля;

5) формирование рекомендаций и выводов.

2.2 Вектор траста и особенности его использования в МПДК

В рамках продольного движения экипажа в плоскости развёртывания угла тангажа β вектор траста FT раскладывается на две ортогональные компоненты FTx и FTz

(1)

Угол наклона вектора FT

(2)

При этом угловой диапазон обметания вектора траста составляет в общем случае от 0° до 360° (квадранты I и IV – тяга вперед, квадранты II и III – тяга назад, при этом квадранты I и II – лифт, квадранты III и IV – антилифт). Ограничимся приземным (без отлета) движением квантомобиля (0 ≤ FTz ≤ Gq, где Gq – вес экипажа) по горизонтальной ОП. Также, приняв вертикальные перемещения ТС при наземном движении несущественными (в сравнении с его горизонтальными перемещениями), освободимся от учета динамики вертикальных перемещений ТС.

2.3 Силовой баланс квантомобиля

В качестве основы модели движения экипажа по горизонтальной ОП выбран следующий вариант уравнения силового баланса квантомобиля

(3)

где FTx – продольная сила тяги КД (траст), Н;

Fr – сила сопротивления качению опорных колес, Н;

Fwx – сила сопротивления воздуха продольному движению (drag), Н;

Fa – сила инерции, противодействующая ускорению экипажа, Н;

Gq' – сила давления экипажа на ОП с учетом лифта/антилифта, Н;

fk0 – коэффициент сопротивления качению колес при нулевой скорости;

fkv – скоростной коэффициент сопротивления качению колес, с2/м2;

Vq – текущая скорость продольного движения экипажа, м/с;

cd – коэффициент аэродинамического сопротивления, безразмерный;

ρw – плотность воздуха, Н ×с2/м4;

Sfront – лобовая площадь экипажа, м2;

Gq – исходный вес (сила тяжести) экипажа, Н;

g – ускорение свободного падения, м/с2;

a – продольное ускорение экипажа, м/с2; 

δwh – коэффициент инерции вращения опорных колес экипажа.

Детализируем величину Gq', а именно:

(4)

где Fwz – аэродинамическая подъемная сила, Н. Для квантомобиля приведенная масса m’ = Gq(1+δwh)/g учитывает только вращение опорных колес, поскольку вращающиеся детали силового привода отсутствуют.

Отметим, что

Также отметим, что при представлении выражений программного алгоритма (представляемого на Simulink-схемах) используется нотация Simulink (прямая латиница, без индексов). например:

(5)

График прикладываемых к экипажу сил отображен на рис. 2. Обозначены: Vq – скорость движения экипажа; V∞ – скорость невозмущенного воздушного потока относительно экипажа

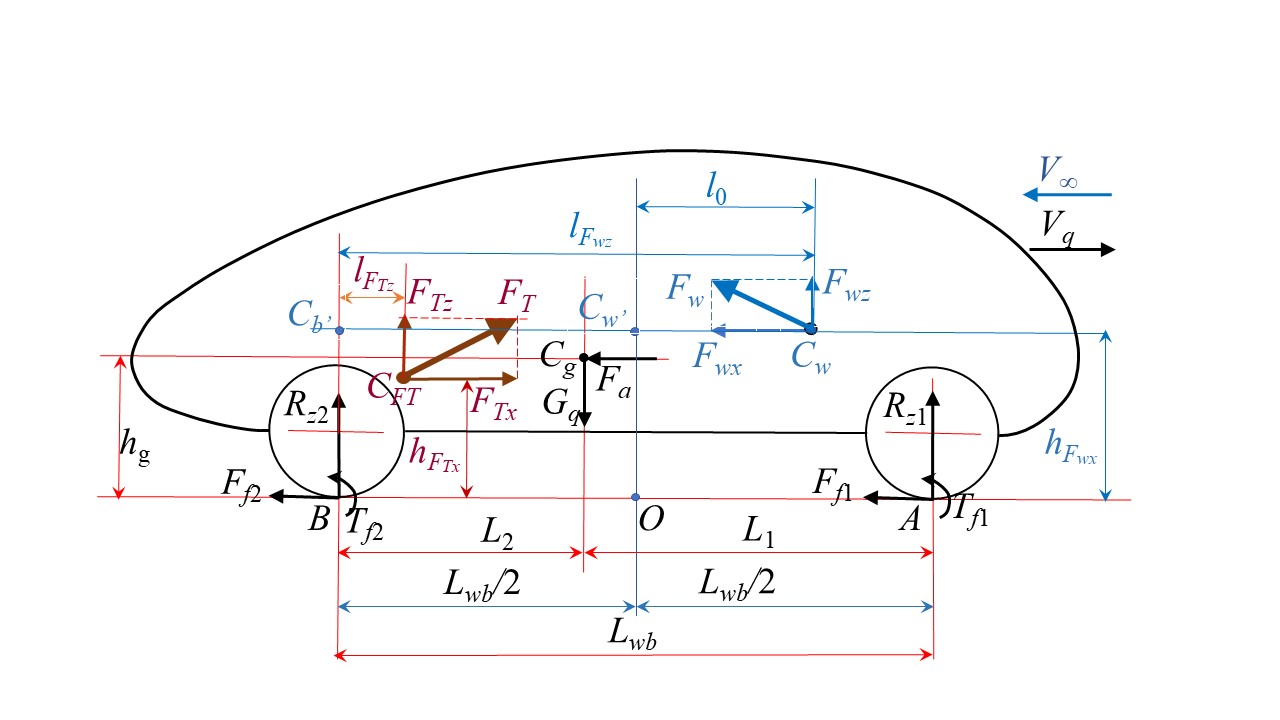
Рисунок 2 - Схема сил, действующих на квантомобиль

DOI:10.23670/IRJ.2023.136.24.2

2.4 Баланс моментов сил, действующих на квантомобиль

Формирование опрокидывающих моментов квантомобиля разберем с помощью рис. 2. Из характерных точек, используемых обычно при анализе баланса моментов – ЦТ (Cg) или точки контакта колес с ОП (A либо B) – выбираем точку контакта с ОП задних колес

Сумма моментов относительно точки B

(6)

Учтем, что ,

(7)

где rд – динамический радиус колеса.

Коэффициент сопротивления качению

Реактивный момент, возникающий в движении от действия нормальной реакции ОП на колеса передней оси (относительно точки B)

(8)

не является искомым питч-моментом, поскольку опрокидывающее воздействие производит момент MΣpm=Lwb·(Rz1–Rz2)/2. И требуемый (requested) стабилизирующий момент (ТСМ) тогда равен Mz1req = –MΣpm.

Для оценки значимости аэродинамического момента MFw = MFwx+MFwz относительно ТСМ Mz1req ввели коэффициент

(9)

2.5 Адаптация МПДК к форме представления результатов испытаний автомобилей

Необходимым явился учет в МПДК формы представления результатов аэродинамических испытаний автомобилей, отображенной ниже.

Фронтальное сопротивление (драг) представляется выражением 

(10)

где Q – скоростной динамический напор;

воздействие силы лифта на экипаж

(11)

аэро-питч-момент

(12)

где cd, cl и cm – коэффициенты драга, лифта и аэро-питч-момента, получаемые по результатам испытаний объектов в аэродинамической трубе (в данном исследовании считаем их постоянными во всем диапазоне скоростей).

Замысел состоял в том, чтобы в МПДК использовать данные по этим коэффициентам, зафиксированные для автомобилей в стендовых условиях.

На высоте hFwx (см. рис. 2) существует ЦД Cw сил Fwz и Fwx – на расстоянии lFwz от вертикальной плоскости задней оси и расстоянии lO от вертикальной плоскости центра колесной базы.

По теореме Пуансо можно перенести силу Fwz в точку Cw' на вертикальной плоскости центра колесной базы (это будет сила Fl=Fwz), с возникающим при переносе моментом сил MFl . 

Выявим связь координаты ЦД по горизонтали с результатами испытаний модели ТС в аэродинамической трубе следующим образом. Убедимся в возможности разложения на две составляющие коэффициента cm = cmd+cml:

,

где MFd – момент драга Fd относительно ОП, MFl – момент смещения силы лифта Fl с появлением плеча lO.

Теперь можем записать:

Отсюда получим:

(13)

Далее, перемещение тем же способом силы Fwz из точки Cw' в точку Cb' добавит момент приводя к сумме:

После сокращения получаем .

Откуда горизонтальная координата ЦД в ССК:

(14)

Рассмотренные на базе теоремы Пуансо особенности горизонтального смещения силы лифта Fl (Fwz) верны и для других вертикальных сил схемы рис. 2: Gq и FTz. И поскольку аэро-питч-момент в стендовых условиях определяется с опорой на колесную базу Lwb с центром в точке O, то и моменты других вертикальных сил должны рассчитываться с плечами относительно точки O, а именно, . Этим из общего баланса моментов сил (6) вычленяется совокупность воздействий, образующих только опрокидывающий момент MΣpm.

2.6 Влияние высоты действия траста КД на питч-момент 

В практике испытаний моделей автомобилей в аэродинамической трубе опорные элементы модели крепят к опорному столу

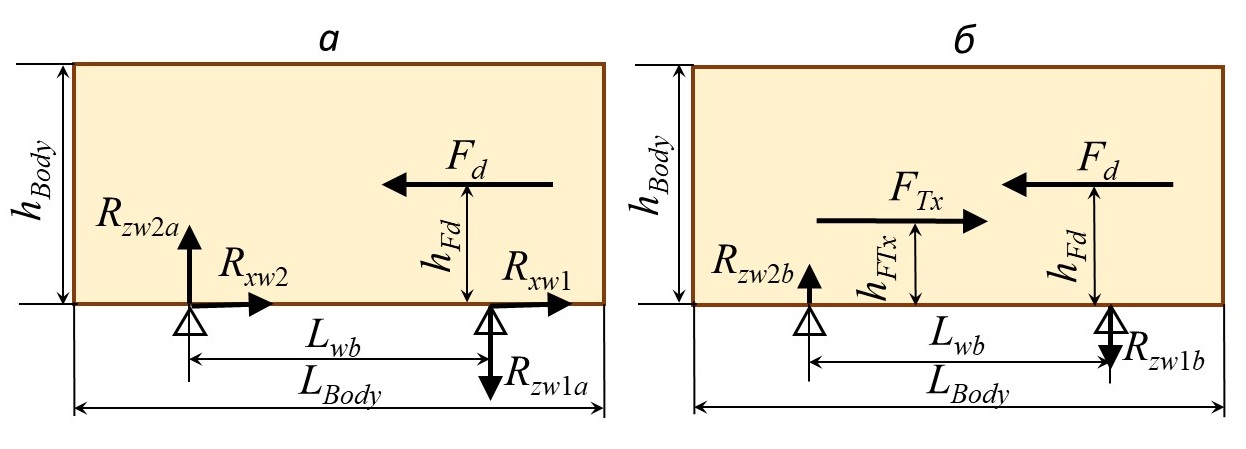
Рисунок 3 - Схемы баланса сил, действующих на тело:

а) – закрепленное в аэродинамической трубе к ОП стола; б) – с имитацией траста FTx, действующего над ОП

DOI:10.23670/IRJ.2023.136.24.3

Оценим соотношение сил и моментов на рис. 3a. с подключением коэффициентов cd и cm. В отсутствие лифта имеем: и . Используя равенство этих моментов, получим: . Отсюда можно определить высоту ЦД для модели произвольного масштаба (при посткритических числах Re

[21]

,

[22]

): 

(15)

Для перехода ко второй ситуации (по рис. 3б) необходим учет изменения питч-момента из-за вывешивания силы FTx над ОП на высоту hFTx. Тогда результирующий аэро-питч-момент:

(16)

2.7 Simulink-модель приземного движения квантомобиля (МПДК)

Рассмотренный аналитический материал привлечен для формирования имитационной системы МПДК, две подсистемы которой – Vehicle Dynamics (рис. 4) и NormReactions (рис. 5) – усовершенствованы (относительно

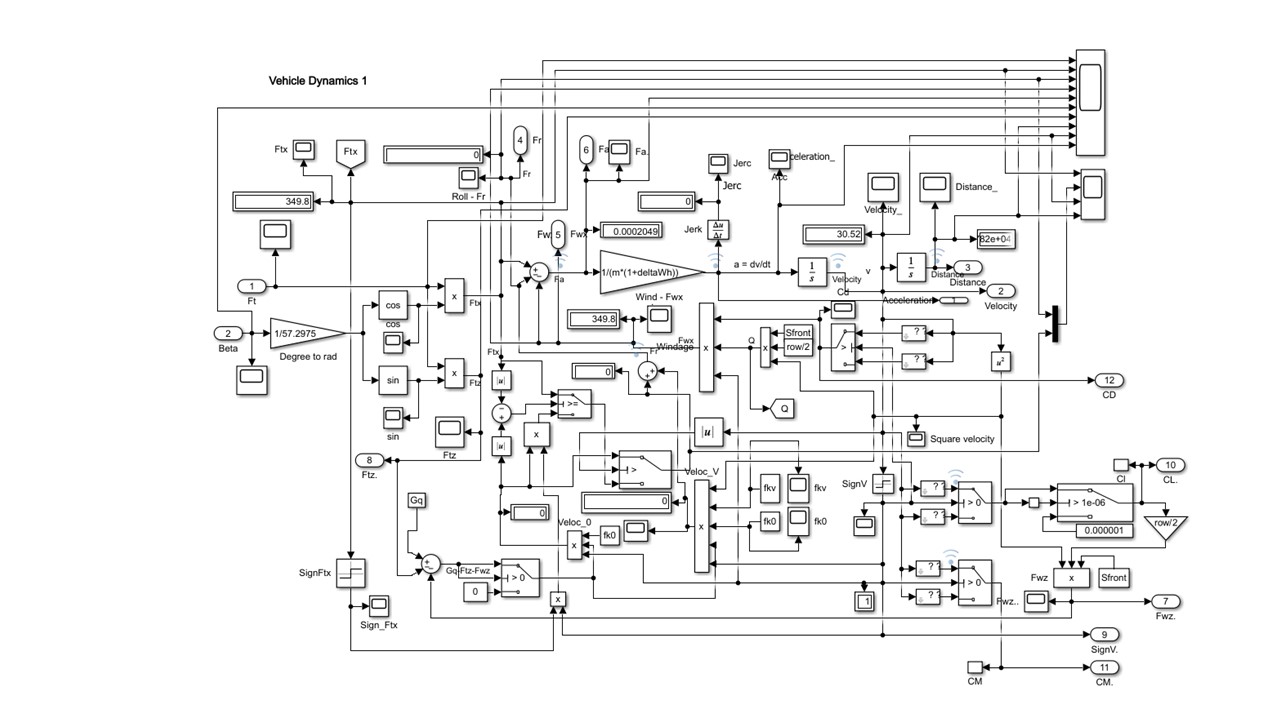
Рисунок 4 - Подсистема Vehicle Dynamics расчета показателей движения

DOI:10.23670/IRJ.2023.136.24.4

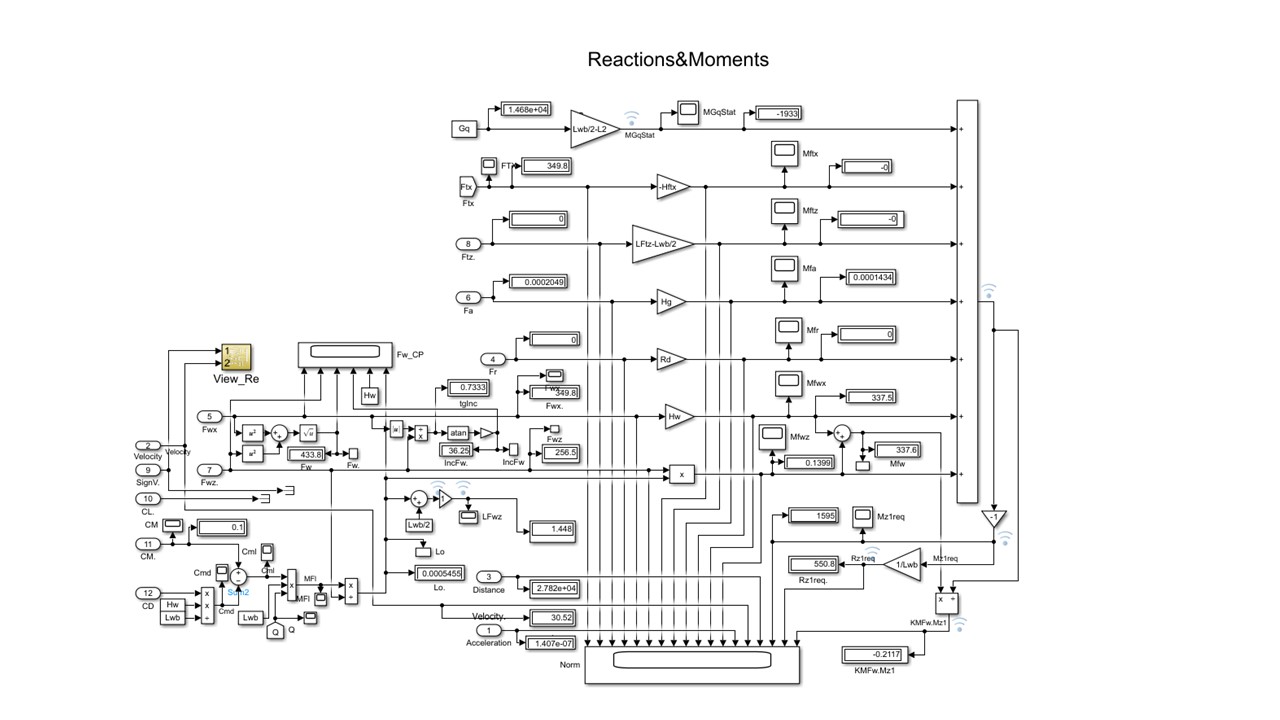
Рисунок 5 - Подсистема NormReactions расчета силовых моментов

Примечание: зафиксировано состояние при моделировании обдува на стенде ТС Баруха: V∞ = 30,5 м/с; Ftx =349?8 H; HFtx = 0 м

DOI:10.23670/IRJ.2023.136.24.5

2.8 Верификация использования результатов аэродинамических испытаний автомобиля при настройке МПДК

Верификация программы МПДК под вариант моделирования стендовых испытаний состояла в реинжиниринге в среде ПИМ состояния автомобиля, закрепленного на столе стенда (с отключенным блоком качения колес: fk0=0, fkv=0). При этом задавали высоту траста КД hFTx = 0 (нереальная высота для КД квантомобиля, но вариант представления тяговой силы, реализуемой ведущими колесами автомобиля в точках контакта с ОП). Задавали зафиксированные в натурном эксперименте значения коэффициентов cd, cl, cm. Далее, подобрав соответствующую силу тяги FTx, выполняли разгон виртуальной модели, заканчивающийся установившимся движением на скорости V∞ обдува натурной модели в трубе. Оценивали сходимость и невязки натурных и виртуальных экспериментов.

В качестве иллюстрации методики приведем действия на базе примера из классической работы Баруха

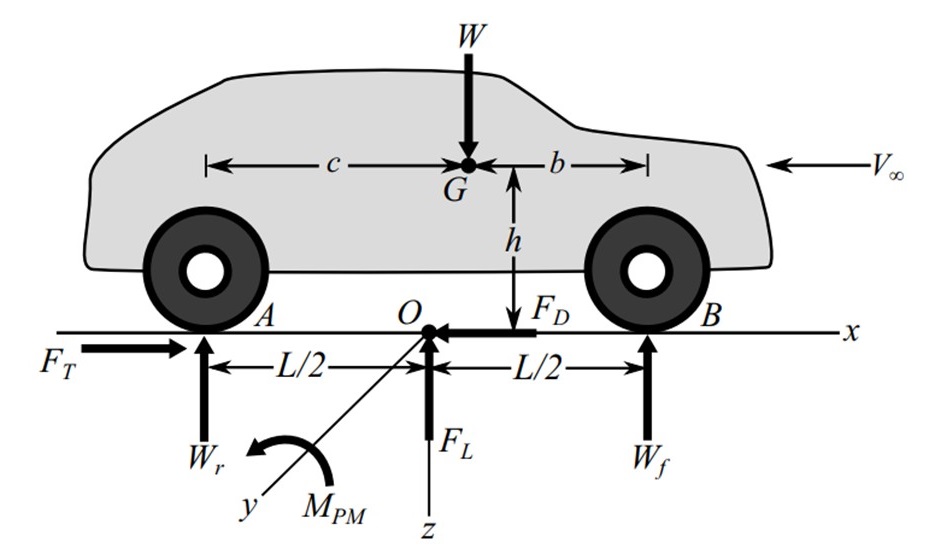
Рисунок 6 - Схема сил и моментов, действующих на автомобиль, закрепленный к столу аэродинамической трубы

DOI:10.23670/IRJ.2023.136.24.6

Исходные данные автомобиля (с переводом данных Баруха в систему SI): Вес автомобиля в статике W = 3300 lb (14678 Н); вес по осям: Wf = 1800 lb (6672 Н), Wr = 1500 lb (8006 Н); Lwb= 9,5 ft (2,8956 м); Sfront = 22 ft2 (2,044 м2). Величины, измеренные Барухом на стенде, приведены в табл. 1.

Скоростной напор для скорости V = 30,48 м/с; Q = (ρ/2)SfrontV2 = 0,6125·2,044·30,482 = 1163 Н. Оценка cd = FT/Q = 349,8/1163 = 0,3. Oценка cl = Fl/Q = (245+11)/1163 = 0,22. Оценка питч-момента для скорости V = 30,48 м/с по формуле Баруха

Далее, в МПДК ввели в исходных данных cd = 0,3, cl = 0,22, cm = 0,1. Вычислили hFd = cm·Lwb /cd = 0,1·2,8956 / 0,3 = 0,9652 м. Реализовали имитацию разгона модели ТС (иначе – воздушного потока) c трастом FTx = 349,8 H (иначе – драга FD) до установившегося движения (соблюдая условие: fk0 = 0, fkv = 0).

Результаты имитации можно видеть на распечатке конечного состояния подсистемы Reactions&Moments в режиме виртуального установившегося движения ТС Баруха (точнее, потока воздуха относительно закрепленного экипажа) – рис. 5. На рис. 7 представлены графики виртуального разгона (точнее – потока воздуха) ТС Баруха и квантомобиля.

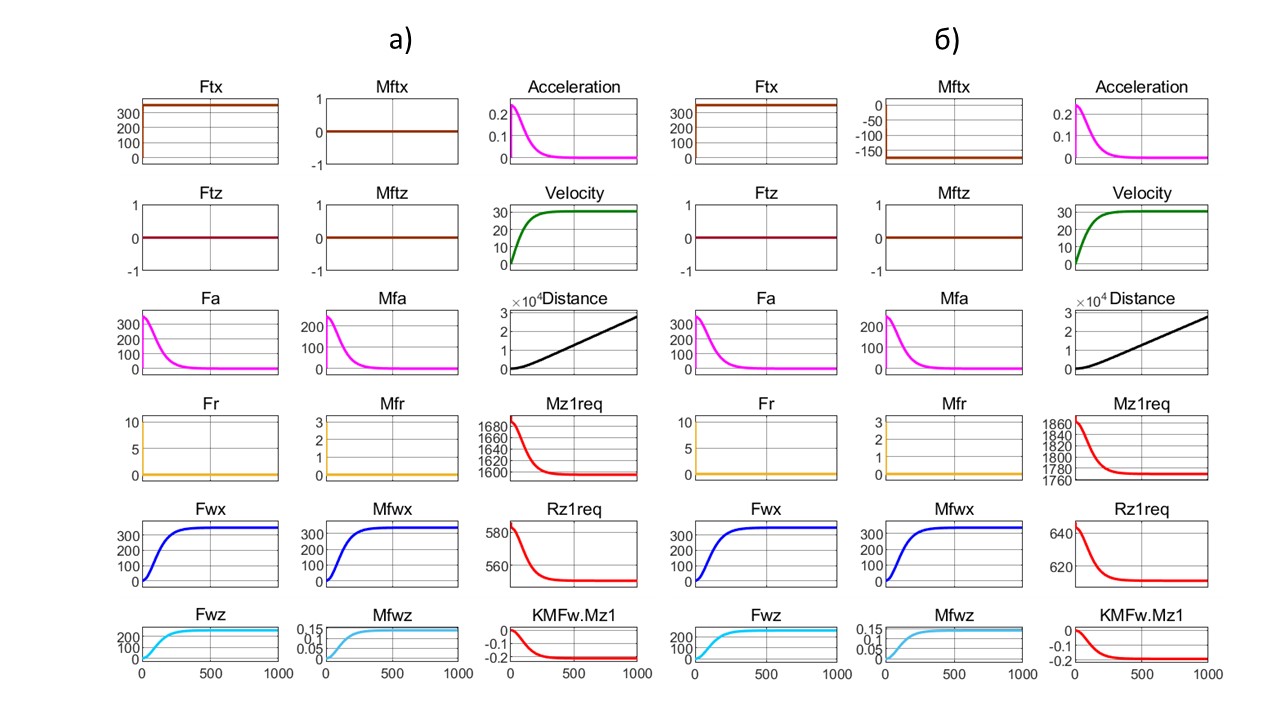
Рисунок 7 - Графики виртуального разгона ТС под условия стенда с конечной установившейся скоростью обдува V∞ = 30,5 м/с (сd = 0,3; сl = 0,22; сm = 0,1; fk0 = 0, fkv = 0):

а) автомобиль – HFtx = 0 м; б) квантомобиль – HFtx = 0,5 м

DOI:10.23670/IRJ.2023.136.24.8

Основные результаты ПИМ, совместно с результатами расчета показателей по данным Баруха, помещены в сравнительную таблицу 2. Отмечена высокая сходимость показателей, что явилось основанием расширения полигона ПИМ по исследованию аэродинамических показателей – возможность выхода за пределы рамочного (стендового) режима.

С целью количественной оценки динамики и продольной устойчивости квантомобиля посредством МПДК провели расчеты разгонов с выходом на установившийся режим. Опорными выбрали значения траста: для рамочного исследования аэродинамики (имитации условий стенда с отсутствием качения колес) – FT = 349,8 Н; для исследования динамики и устойчивости движения в дорожных условиях – FT = 1500 Н. Базовые данные автомобиля-прототипа и среды: Gq = 14680 Н; Lwb = 2,8956 м; Sfront = 2,044 м2; δwh = 0,04; fk0 = 0,02; fkv = 0,00037 с2/м2; ρw = 1,225 Н×с2/м4. Базовыми значениями параметров квантомобиля (однако варьируемых попеременно в той или иной серии расчетов), явились следующие: Hftx = 0,5 м; Lftz = 0,05 м; ; β = 0º; fk0 = 0,02; fkv = 0,00037 с2/м2; cd = 0,3; cl = 0,22; cm = 0,1.

3.1 ПИМ в рамочном режиме (с трастом FT = 349,8 Н)

Для оценки влияния аэро-питч-момента на устойчивость автомобиля (Hftx = 0) и квантомобиля (Hftx = 0,5) выполнили ряд имитаций МПДК в рамочном режиме с перебором значений cm в диапазоне –0,1÷0,15. Результаты см. рис. 8.

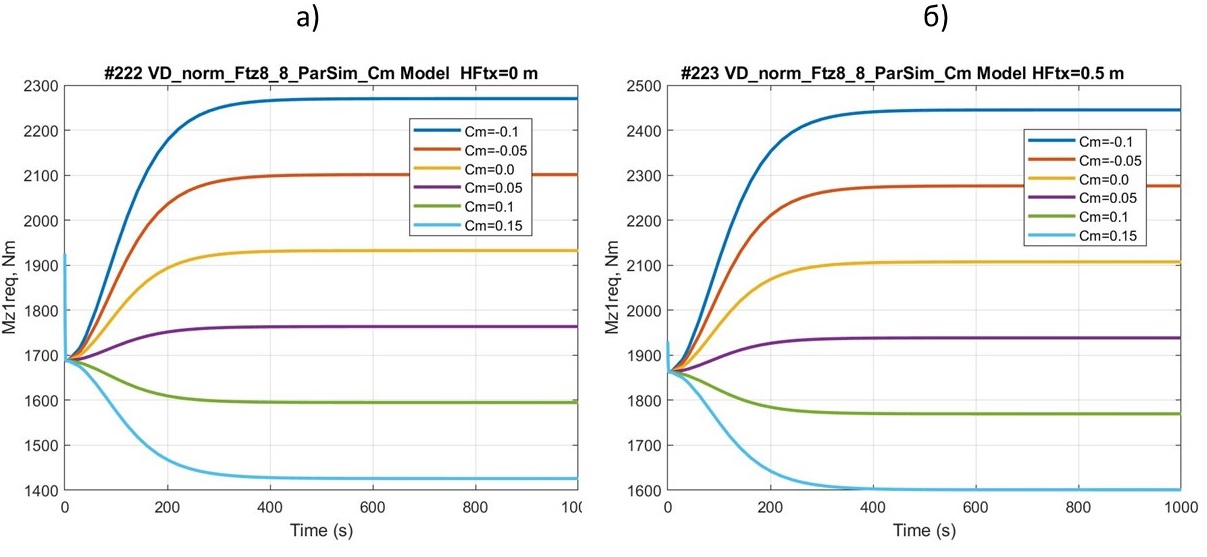
Рисунок 8 - Графики зависимости ТСМ Mz1req от значений коэффициента cm:

а) для автомобиля; б) для квантомобиля – при различных cm (fk0 = 0, fkv = 0)

DOI:10.23670/IRJ.2023.136.24.10

Для оценки влияния высоты действия траста на устойчивость квантомобиля провели серию имитаций с варьированием величины hFTx: от 0 м («автомобильный» вариант) до 0,8 м. Результаты зафиксированы на рис. 9.

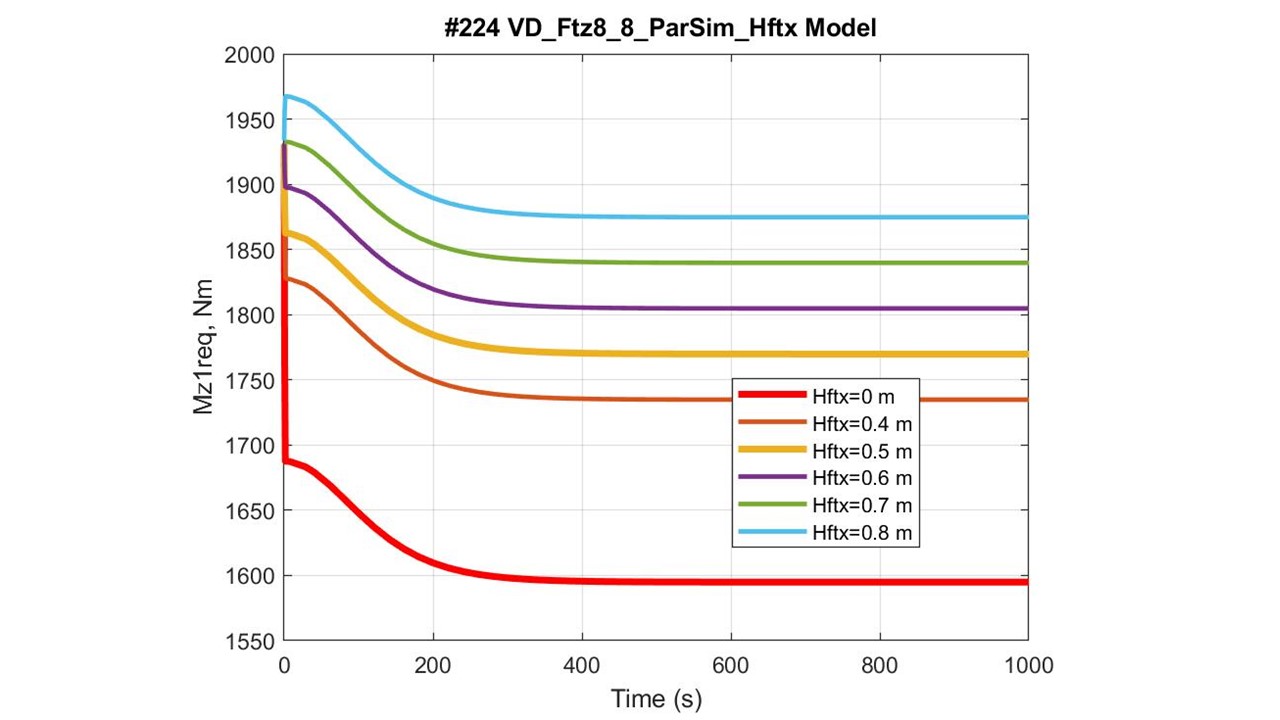
Рисунок 9 - Графики зависимости ТСМ Mz1req от высоты приложения тяговой силы: для автомобиля (Hftx = 0 м) и квантомобиля (Hftx = 0,4÷0,8 м)

DOI:10.23670/IRJ.2023.136.24.11

Значение траста Ftx = 349,8 Н, обеспечивающее баланс сил при обдуве ТС Баруха на стенде со скоростью V∞ = 30,5 м/с, имеет недостаточную тягу для обеспечения баланса сил при подключении сопротивления качению колес. Уже при fk0 = 0,03 (применительно к дорожным условиям) экипаж не сможет преодолеть силу трения покоя колес и тронуться с места. Проведя серию расчетов по рамочному исследованию аэродинамических сил и коэффициентов для подключения факторов движения в дорожных условиях, перешли к уровню силы тяги, близкому к максимальному для ТС класса автомобиля Баруха – 1500 Н. При этом для квантомобиля, в отсутствие трансмиссии, производим моделирование всего разгона экипажа с этой тягой (обоснование см. в

[15]

).

3.2 ПИМ движения в дорожных условиях (с трастом FTx = 1500 Н)

При моделировании движения экипажа в дорожных условиях, естественно, задается уровень сопротивления качению колес.

На рис. 10 представлена обобщенная картина зависимости ТСМ Mz1req в процессе разгона ТС (автомобиля-аналога (а) и квантомобиля (б)) от значений коэффициента fk0. Использованы аэродинамические коэффициенты, характеризующие экипаж без специальных аэродинамических средств (САС): cd = 0,3; cl = 0,22; cm = 0,1.

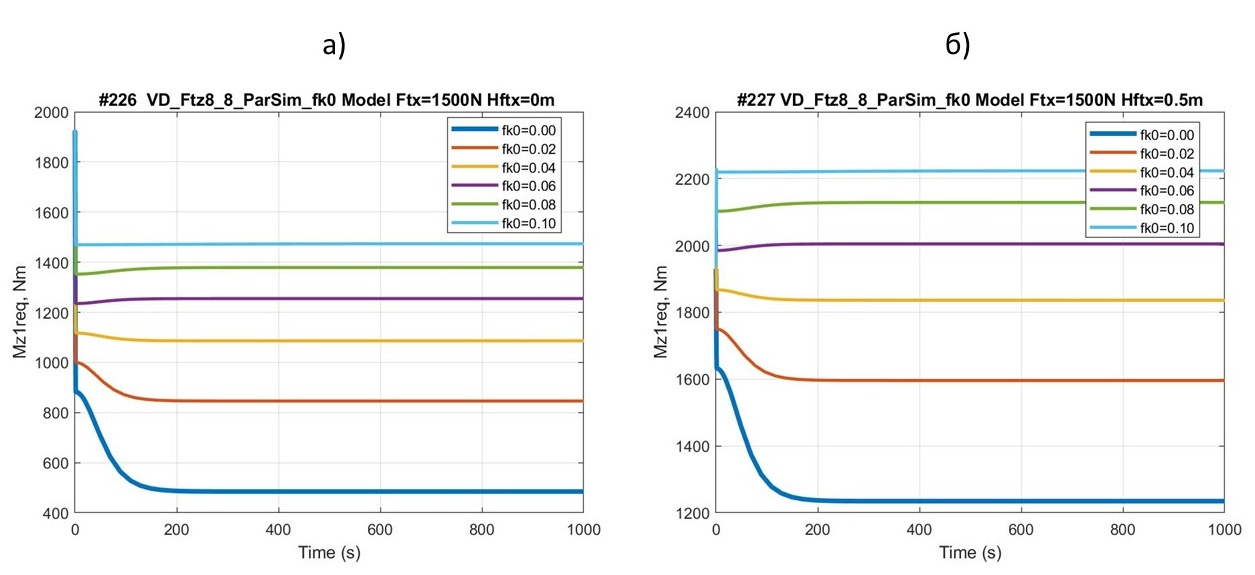
Рисунок 10 - Сравнительная картина зависимости ТСА Mz1req в процессе разгона ТС (автомобиля-аналога (а) и квантомобиля (б)) – от коэффициента fk0; аэродинамические коэффициенты: cd = 0,3; cl = 0,22; cm = 0,1

DOI:10.23670/IRJ.2023.136.24.12

Для оценки влияния на устойчивость экипажа САС (особая форма кузова и его посадка, делители потока, боковые щитки, диффузоры, крылья и спойлеры, переднее оперение

[24]

,

[25]

,

[26]

,

[27]

) реализован расчет необходимых стабилизирующих моментов для ТС с базовыми параметрами автомобиля Баруха, но с совокупным виртуальным привнесением в его конструкцию всех перечисленных САС. Для этого использованы результаты работы Gallego

[21]

, в которой финальный радикальный вариант с совокупностью названых привнесенных свойств имел значения коэффициентов: cd = 0,574, cl = –0,957, cm = 0,697. Отличие формы Тела Ахмеда

[28]

, использованного Gallego в качестве базовой модели, от формы автомобиля Баруха считаем малозначимым фактором, поскольку во множестве вариантов трансформации Тела Ахмеда

[22]

,

[29]

,

[30]

,

[31]

всегда можно получить форму с аэродинамическими коэффициентами автомобиля Баруха.

На рис. 11 представлена картина зависимости ТСМ Mz1req в процессе разгона ТС ((а) автомобиля-аналога с привнесенными свойствами и (б) квантомобиля с этими же свойствами) от значений коэффициента fk0.

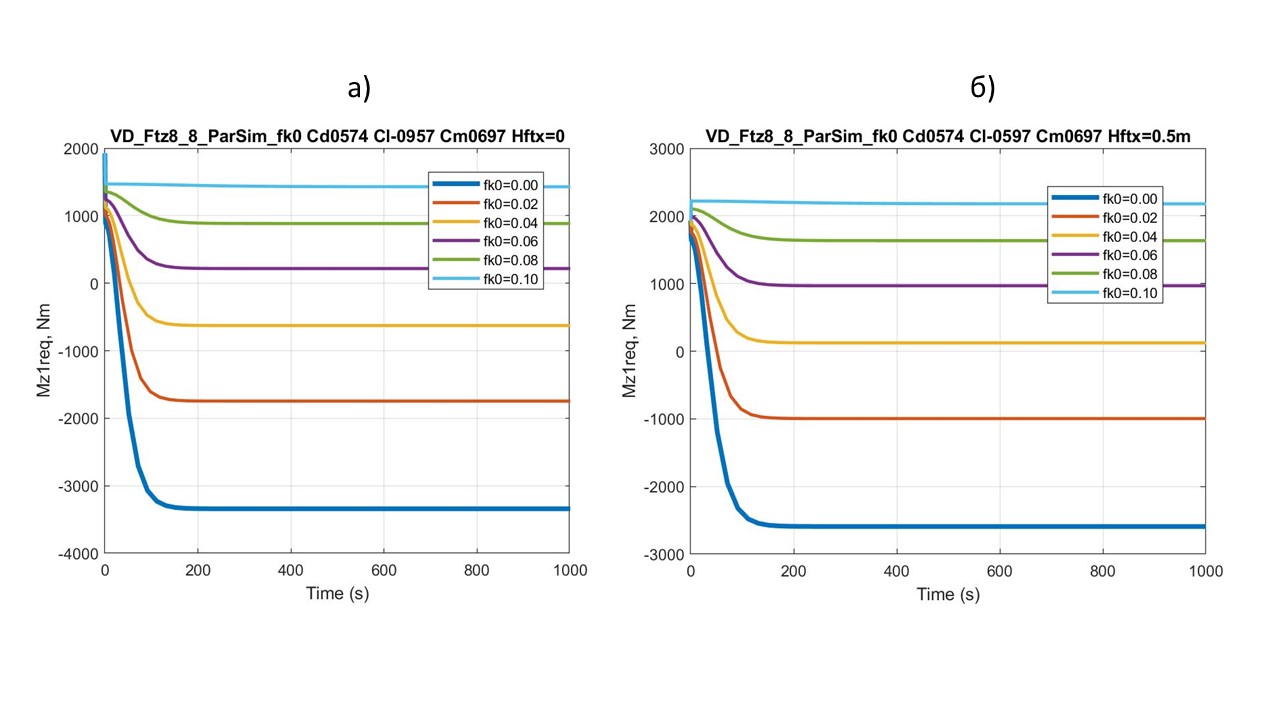
Рисунок 11 - Сравнительная картина зависимости ТСМ Mz1req в процессе разгона ТС с САС ((а) автомобиля-аналога и (б) квантомобиля) – от коэффициента fk0; аэродинамические коэффициенты: cd = 0,574; cl = –0,957; cm = 0,697

DOI:10.23670/IRJ.2023.136.24.13

На рис. 12 представлена картина зависимости ТСМ Mz1req от угла наклона вектора траста β, в процессе разгона квантомобиля с выходом на установившуюся скорость 50,5 м/с при fk0 = 0,02. Этой скорости экипаж достигает при горизонтальном трасте (β = 0°) Ftx = 1500 Н. При β > 0° появляющаяся сила Ftz > 0 уменьшает величину G'q, определяющую сопротивление качению колес (см. (4)). В этом случае для достижения названной скорости достаточный уровень Ftx < 1500 Н. Использовали способность МПДК рассчитывать необходимый уровень Ftx в этой ситуации. Для вычисления соответствующего значения Ftz привлекали обращение зависимости (2).

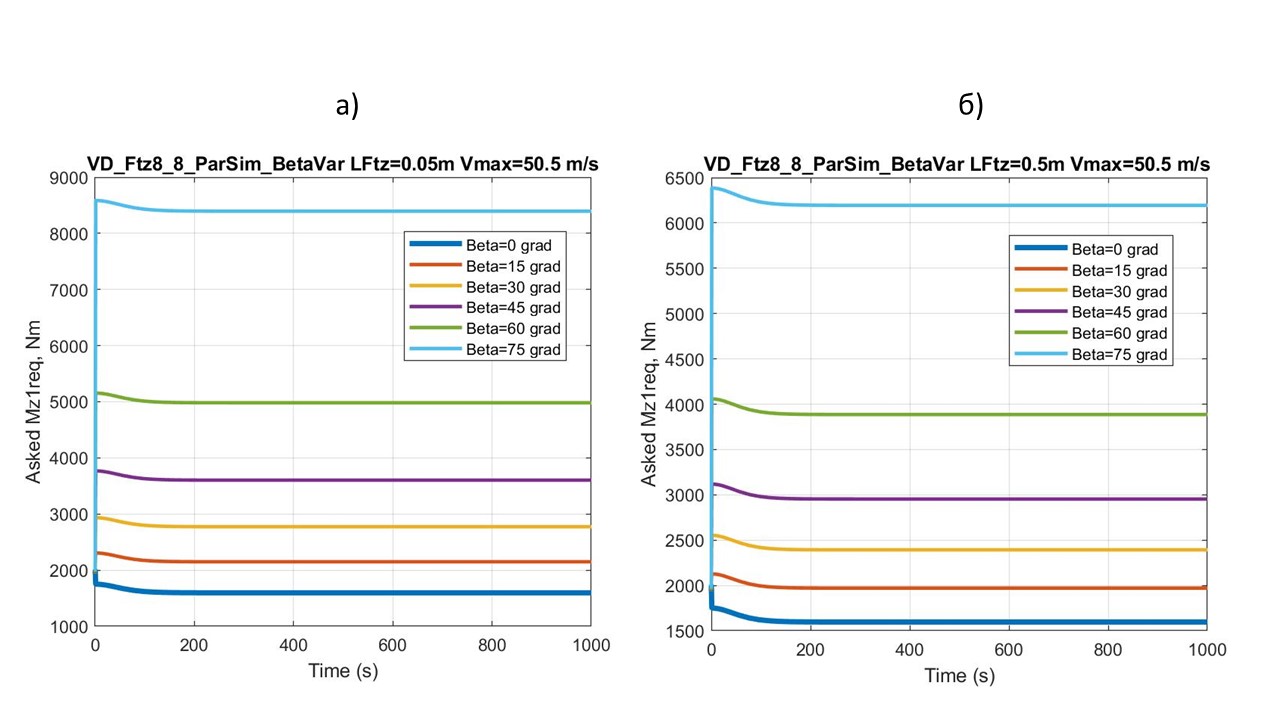
Рисунок 12 - Графики зависимости ТСМ Mz1req от угла наклона вектора траста β, в процессе разгона квантомобиля с выходом на крейсерскую скорость 50,5 м/с при fk0 = 0,02:

а) горизонтальная координата точки приложения траста LFtz = 0,05 м; б) точки приложения LFtz = 0,5 м

DOI:10.23670/IRJ.2023.136.24.14

Представленные результаты являются отражением действий автора по развитию концепции квантомобиля. Эта концепция возникла в трудах Леонова В.С.

В этих работах закладывались основы Simulink-моделирования движения квантомобиля, настраивались объекты-прототипы из числа существующих наземных ТС, главным образом модели КамАЗ-4326

Влияние коэффициента cm (см. рис. 8) на устойчивость – существенно. В диапазоне его варьирования от –0,1 до +0,15 размах изменений аэро-питч-момента у автомобиля составляет 850 Нм. Такой же размах будет и у квантомобиля, что для него более ущербно. Вполне понятно, что рост величины ТСМ Mz1req (в положительном направлении) связан с изменением аэро-питч-момента (и величины cm) в отрицательную сторону.

Значимость высоты действия траста (см. рис. 3) на устойчивость квантомобиля (см. рис. 9) оценим посредством количественного рассмотрения расчетного баланса моментов. Для автомобиля на стенде (Hftx = 0 м) ТСМ Для квантомобиля (Hftx = 0,5 м) ТСМ В данном случае величина «клюющего» момента MFtx = 175 Нм по модулю составила примерно половину момента сил сопротивления воздуха MFw и десятую часть статического момента смещения центра тяжести экипажа относительно середины колесной базы MGqStat.

Заслуживает внимания сравнительная картина зависимости ТСМ Mz1req (автомобиля-аналога и квантомобиля) от значений коэффициента дорожного сопротивления качению колес fk0 (см. рис. 10). По сути, семейство кривых, характеризующих квантомобиль (рис. 10б), эквидистантно семейству кривых для автомобиля-аналога (рис. 10а). Оно всё смещено на величину ΔMz1req = FTx·HFTx = 1500Н·0,5м = 750 Нм. Объяснимо всё тем же «клюющим» моментом, создаваемым трастом КД. Размах значений ТСМ Mz1req в диапазоне значений fk0 0,0÷0,1 для обоих сравниваемых вариантов составляет ≈1000 Нм. Следует отметить, что зафиксированные на рис. 10 кривые разгона экипажей из-за различия значений fk0 при FTx = const заканчиваются разной конечной скоростью установившегося движения – более детализированный анализ топологии данных семейств отнесен автором на будущее.

Похожей оказалась и сравнительная картина зависимости ТСМ Mz1req в процессе разгона ТС с САС (автомобиля-аналога и квантомобиля) от значений коэффициента дорожного сопротивления fk0 (см. рис. 11). Семейство кривых, характеризующих квантомобиль (рис. 11б), топологически подобно семейству кривых для автомобиля-аналога (рис. 11а). Оно также всё смещено на свою величину ΔMz1req. Однако размах значений ТСМ Mz1req в диапазоне значений fk0 0,0÷0,1 для этих сравниваемых вариантов составляет ≈ 4800 Нм.

Таким образом, привнесение САС в конструкцию квантомобиля (нацеленное специально на создание максимально возможного прижатия экипажа к ОП

Зависимость ТСМ Mz1req от угла наклона вектора траста β (см. рис. 12) оказалась значимой. Анализ перемещения точки приложения траста вперед, к центру колесной базы (в примере c LFtz = 0,05 м до LFtz = 0,5 м) – позволил отметить, по крайней мере, два момента. Во-первых, это приводит к снижению ТСМ для всех углов β > 0° (особенно при больших углах – сравните 6200 Нм и 8300 Нм для β = 75°). Во-вторых, сужает размах значений ТСМ – сравните размах 6800 Нм для LFtz = 0,05 м и размах 4600 Нм для LFtz = 0,5 м.

Естественно, значения MFtz (а следовательно, и ТСМ при прочих равных параметрах) будут наименьшими при нахождении точки приложения траста в области центра колесной базы, но, при наличии противоречий компоновочного характера использование зависимостей типа представленных может явиться элементом соответствующих оптимизационных методик.

Simulink-модель приземного движения квантомобиля (МПДК), созданная на базе рассмотрения схемы сил и моментов, действующих на квантомобиль, позволяет осуществлять проведение расчетных исследований как динамики продольного движения экипажа в дорожных условиях, так и имитации нагрузок в условиях аэродинамического стенда.

В целом, подтвердилась гипотеза: уровень и характер питч-момента квантомобиля отличается от такового для автомобиля. Он может быть значительным, иногда меняя направленность (относительно автомобильного варианта ТС) и требует его оперативной нейтрализации (минимизации).

На основе результатов ПИМ показана значимость проблемы обеспечения продольной устойчивости квантомобиля. Основными факторами, усугубляющими названую проблему, в сравнении с классическим автомобилем, являются возникновение и реализация тяговой силы над опорной поверхностью, что увеличивает опасность опрокидывания экипажа.

Для нейтрализации опрокидывающих моментов необходимы дополнительные вертикальные трастеры и другие средства, охватываемые единой системой управления с основным КД. 

Основные средства управления аэродинамическим воздействием на экипаж: жесткие конструктивные элементы (обводы и оперение корпуса); выдвижное оперение; дополнительные стабилизирующих трастеры – как показали проведенные расчеты, способны существенно изменять питч-моменты квантомобиля, с увеличением зависимости их от дорожных условий.

Сформированные на базе программы МПДК методические положения оценки продольной устойчивости квантомобиля могут послужить основой расчетной оптимизации компоновок этого вида ТС, расположения силовых модулей (трастеров) и САС, задействования их в процессе движения.

Сформирована методика использования существующих материалов испытаний автомобилей-аналогов для прогнозирования устойчивости квантомобилей.

Расчеты в среде МПДК позволили преодолеть познавательную сложность отображения и количественной оценки параметров продольного движения гипотетического квантомобиля. МПДК можно рассматривать как важную компоненту структуры дальнейших исследований квантомобиля.