An Evaluation of the Effectiveness of Didactic Model of Teaching the Discipline "Descriptive Geometry and Engineering Graphics" with the Elements of Creative Thinking Activation
An Evaluation of the Effectiveness of Didactic Model of Teaching the Discipline "Descriptive Geometry and Engineering Graphics" with the Elements of Creative Thinking Activation
Abstract
This article evaluates the effectiveness of a didactic model of teaching the discipline "Descriptive Geometry and Engineering Graphics" using a set of tasks aimed at activating creative thinking. The check of students' knowledge mastering after the course was carried out. The experimental verification included several stages and three types of experiments. The level of students' competence was evaluated on the basis of evaluation criteria of end-of-term control, results of control and examination works. With the help of specially designed knowledge tests and residual level tasks, the strength and durability of the acquired knowledge, as well as the formation of methodological knowledge and activity skills were reviewed. The results of the study showed that the application of the developed didactic model of teaching with a set of tasks contributes to the improvement of students' competence level. Experimental groups who were taught according to this model demonstrated a higher level of graphic literacy and better results in comparison with control groups. Moreover, the residual level of students' knowledge and skills one year after the end of the classes was also higher in the experimental groups.
1. Введение
Основное направление исследований состояло в выявлении эффективности дидактической модели преподавания и поддержания учебной мотивации при изучении дисциплины «Начертательная геометрия и инженерная графика» с использованием учебного комплекса задач с элементами активизации творческого мышления.
Опытная проверка эффективности дидактической модели проводилась в течение 2020-2021 и 2021-2022 учебных годов в ФГБВОУ ВО «Академии гражданской защиты МЧС России» на кафедре механики и инженерной графики. Были задействованы четыре группы обучающихся: две группы по направлению 20.03.01 «Техносферная безопасность» и две группы 25.03.03 «Аэронавигация».
Обучаемым по «Техносферной безопасности» (экспериментальные группы) было предложено изучать дисциплину с применением дополнительного комплекса заданий, включающих в себя лекционный материал, задачи повышенной сложности, задачи с элементами творческого мышления, тестовые задания, веб-квесты. Обучаемые проходили еженедельную дополнительную проверку знаний
, , .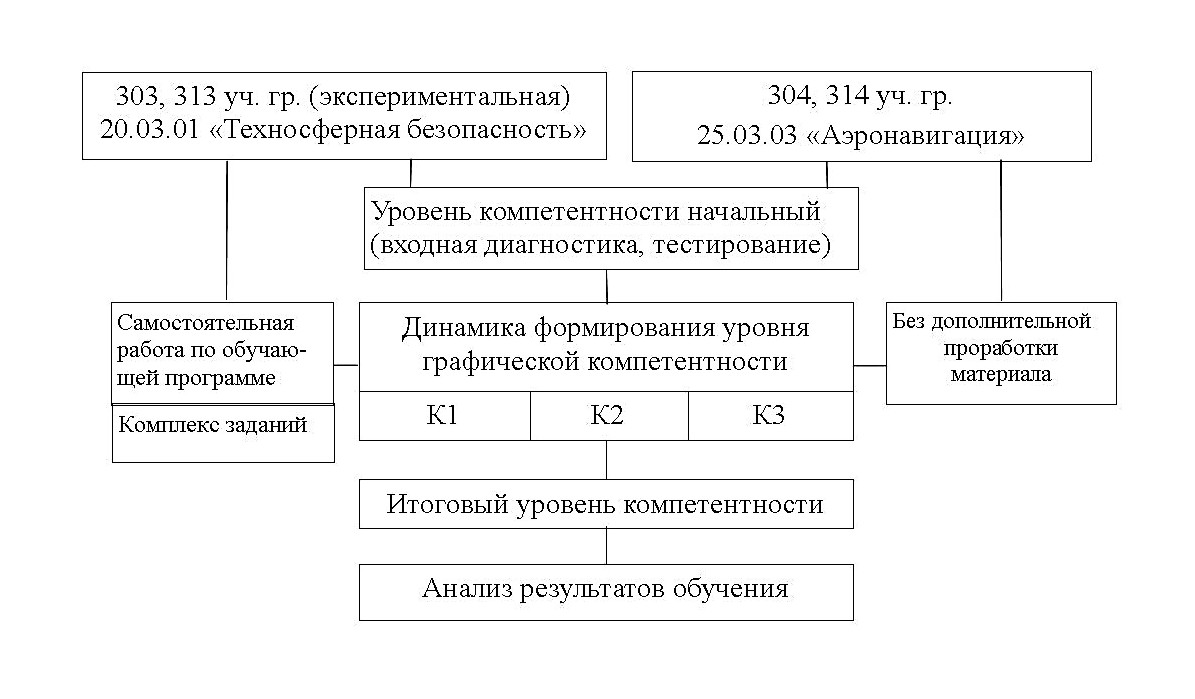
Рисунок 1 - Логическая структура проверки эффективности дидактической модели обучения с использованием комплекса заданий
2. Методы и принципы исследования
В ходе проведения исследования по оценке эффективности дидактической модели преподавания дисциплины «Начертательная геометрия и инженерная графика» с использованием методики В.П. Беспалько
, было обращено внимание на процесс обучения как деятельность, которая разделена на репродуктивную и продуктивную составляющие. В основе этой методики лежит цель усвоения знаний, которые разделены на уровни узнавания, воспроизведения, применения и творчества.Дидактическая система – это организованная педагогическая система, которую представляют взаимосвязанные элементы: образовательные цели; содержание образования и обучения; обучающиеся и их личностные характеристики; обучающие и автоматизирующие средства; организационные формы совместного труда обучающих и обучающихся и дидактические процессы (модели обучения) как способы реализации целей и педагогического процесса в целом .
Модель обучения – это систематизированный комплекс основных закономерностей деятельности обучаемого и преподавателя при осуществлении обучения .
Разработанная дидактическая модель преподавания дисциплины «Начертательная геометрия и инженерная графика» обеспечивает активность преподавателя и обучаемого на уровне субъективных отношений и способствует совместному творчеству, саморазвитию на основе выработки ценностных отношений индивидуальной деятельности и коммуникации в ней, что обогащает аксиосферу участников мотивами их эффективной командной (коллективной, групповой) деятельности и соответственно совершенствует процесс обучения в условиях информационного общества. Творческое мышление шире и глубже охватывает, отражает объективную действительность, чем теоретическое мышление. Творческое мышление отражает диалектику теоретического и практического мышления в их единстве. Творческое мышление – это мышление, результатом которого является открытие принципиально нового или усовершенствованного решения той или иной задачи.
Как утверждает Д. Пойа, существуют две категории мыслей:
1) те, которые мы порождаем активно – посредством акта мышления, обдумывания;
2) те, которые вспыхивают в нашем сознании самопроизвольно.
К последним надо относиться как можно более внимательно, изучать, насколько позволяют ваши способности. Такой анализ позволяет приобретать новые знания. Способ решения задач на активизацию творческого мышления, используемый в дидактической модели, где решение задач начинается с преобразования ее условия к удобному виду, сведению задачи о реальных объектах к математической, с помощью упрощения и абстракции. Анализ исходных данных осуществляется переводом условия задачи из прикладного (физического) русла в чисто математическое. Анализируется способ построения (задания) на чертеже необходимых геометрических образов. Применение сведений из теории, выбор наиболее рациональных (удобных) способов, применение соответствующих логических условий. В дальнейшем происходит реализация решения уже на ортогональном чертеже. Данный этап не только чисто технический, но и логический, приходится выявлять и разрешать противоречия
, .В качестве примера приведем сюжет задачи, цель которой заключалась в сравнении двух линейных величин, расположенных на различных уклонах пересеченной местности
:Два соседа поспорили о том, чей дом находится ближе к дороге. Дом одного соседа, находящийся на склоне горы, задан точкой A, дом другого соседа, находящийся по другую сторону дороги на склоне другой горы, – точкой В. Необходимо решить, кто из них прав, т. е. определить, чей дом ближе к дороге, заданной прямой CD (рис. 2), лежащей между склонами и также расположенной под уклоном к горизонту.
Сюжет задачи содержит техническую проблему – необходимо измерить длину двух отрезков прямых линий, перпендикулярно проведенных от домов к линии дороги. Цель задачи – определение линейных величин при помощи методов начертательной геометрии и их сравнение.
При разработке условия задачи были введены некоторые условности, замена материализованных объектов (дом, дорога) объектами начертательной геометрии (точки, прямая), что позволило применить способы преобразования чертежа , , который является неотъемлемой частью условия задачи.
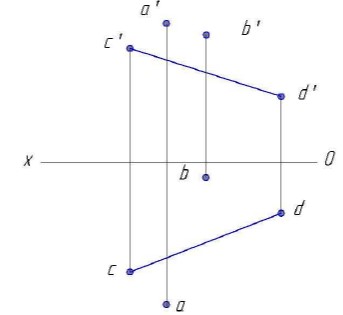
Рисунок 2 - Графическое изображение условия задачи
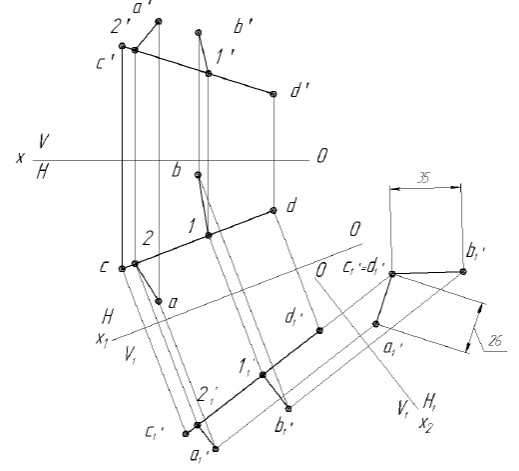
Рисунок 3 - Решение задачи способом замены плоскостей проекций
Участники исследования из всех групп были распределены по типу учебной мотивации на пять подгрупп
, . Оценка ведущего типа мотивации для каждого обучающегося осуществлялась путем подсчета количества ответов «да» для каждого типа мотивации (А – активист, Пр – проектировщик, Ип – испытатель, П – призер, Ил – исследователь). Максимальная сумма баллов указывала на преобладание определенного типа мотивации в учебной деятельности. В случае, если два или более типов набрали одинаковое количество баллов, обучающийся считался полимотивированным, и важный мотив выделялся в индивидуальной беседе со студентом.Для каждого студента был определен конкретный тип мотивации – «Активист», «Проектировщик», «Испытатель», «Призер» или «Исследователь», и данные были подсчитаны для каждой учебной группы. Подробные данные по группам представлены на рисунке 4.
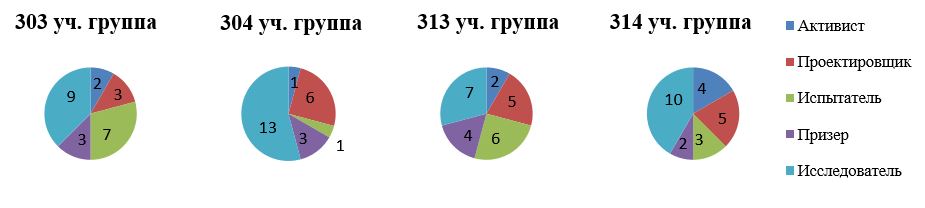
Рисунок 4 - Данные по учебным группам
Данные результаты свидетельствуют о том, что использование комплекса заданий способствует повышению мотивации и активности студентов в процессе обучения. Обращение к индивидуальным особенностям и потребностям каждого студента, а также поддержка самостоятельного мышления и решения задач способствуют более глубокому усвоению материала и развитию компетенций. Положительный тренд в учебной успеваемости подчеркивает эффективность применяемой дидактической модели и поддерживает выводы о ее практической значимости.
В задачах начертательной геометрии с помощью перебора различных подходов и выбора из них оптимального обучаемый учится анализу, выбору наилучшего решения. Овладевает навыками поиска, критического анализа и синтеза информации, применения системного подхода для решения поставленных задач.
По методике Ю.К. Черновой
, на первом этапе проверки эффективности внедряемой дидактической модели для обеспечения сравнимости результатов мы использовали оценочный критерий в виде отношенийгде N – максимально возможное количество баллов за работу, R – количество набранных баллов за работу.
Границы зон уровней компетентности представлены в таблице 1.
Таблица 1 - Границы зон уровней компетентности
Уровень компетентности | Границы зон критерия |
Неудовлетворительный | Y < 0,7 |
Низкий | 0,7 < Y < 0,8 |
Средний | 0,8 < Y < 0,9 |
Высокий | 0,9 < Y < 1 |
3. Основные результаты исследования
На рисунке 5 и 6 представлены графики, иллюстрирующие положительную динамику уровня компетентности экспериментальных 303, 313 уч. группах.
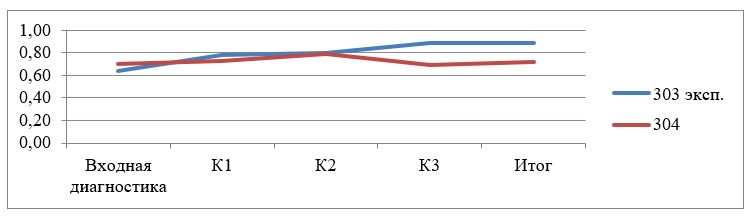
Рисунок 5 - Динамика формирования уровня компетентности групп в 2020-2021 уч. году
Третий рубежный контроль обучаемые экспериментальной группы проходили значительно успешнее.
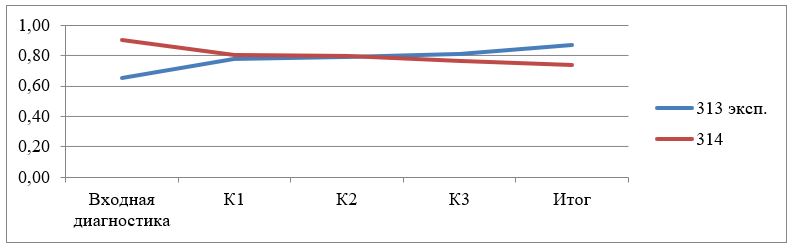
Рисунок 6 - Динамика формирования уровня компетентности групп в 2021-2022 уч. году
После проведения тестированного опроса на первой неделе обучения экспериментальным группам был предоставлен комплекс заданий, который включал дополнительную самостоятельную проработку каждого раздела курса и решение задач повышенной сложности. Студенты работали по этим заданиям в течение 4-6 недель, при этом им предоставлялись дополнительные консультации при необходимости. В то же время обучаемые контрольных групп не выполняли никакой дополнительной проработки материала.
У всех групп проводился четырехуровневый контроль. Последующий анализ успеваемости показал, что разработанная дидактическая модель преподавания привела к повышению уровня сформированности компетенций на 20%. Это свидетельствует о положительном влиянии использования данной модели на процесс обучения и развитие компетенций студентов.
4. Оценка уровня сформированных результатов обучения
Сравнительные данные по остаточному уровню графической грамотности в экспериментальных группах были получены при плановом контроле уровня сформированных результатов обучения в 2021 и 2022 годах (рис. 5).
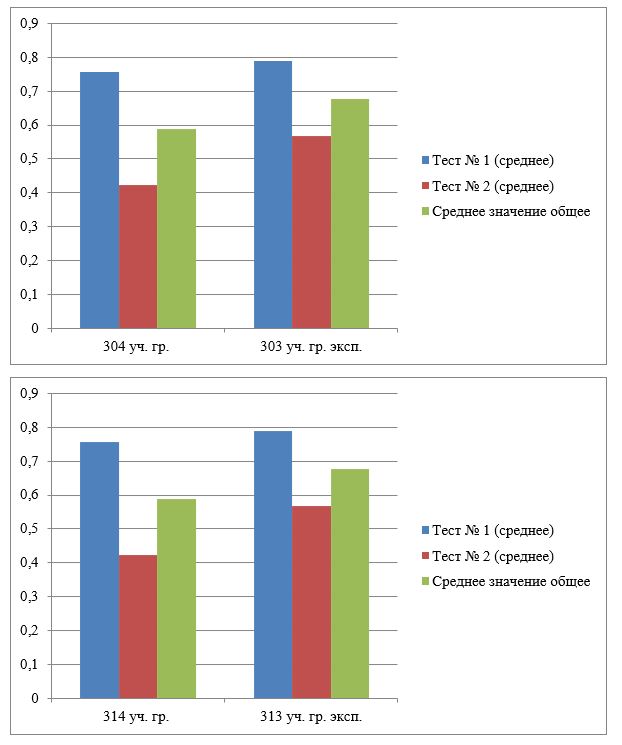
Рисунок 7 - Сравнительная гистограмма остаточного уровня графической грамотности в экспериментальных группах
5. Заключение
Опытно-экспериментальная проверка эффективности дидактической модели преподавания дисциплины «Начертательная геометрия и инженерная графика» с использованием комплекса задач состояла из нескольких этапов и содержала три вида экспериментов. Уровень компетентности устанавливался по оценочным критериям рубежного контроля, результатам контрольных и экзаменов. С помощью специально разработанных тестов и задач остаточного уровня знаний проверялась прочность, долговечность знаний, сформированность методологического знания и деятельностных навыков по истечению года со дня последнего занятия по начертательной геометрии и инженерной графике. По всем показателям и используемым критериям уровень в экспериментальной группе был выше, чем в контрольной.
Таким образом, на основе проведенного исследования можно сделать вывод, что разработанная дидактическая модель преподавания дисциплины «Начертательная геометрия и инженерная графика» с использованием комплекса задач, направленных на активизацию творческого мышления, является эффективным средством формирования компетенций у студентов в указанной области. Эти результаты могут быть полезны для преподавателей и методистов при разработке и внедрении современных подходов к обучению начертательной геометрии и инженерной графики. Для современной подготовки будущего специалиста нужно, помимо передачи «ядра» фундаментальных и профессиональных знаний, специально учить обучаемого мыслить вообще, способам творческого мышления и творческой деятельности в частности.
