RESEARCH ON THE LEVEL OF STUDENT PERFORMANCE USING MULTIVARIATE ANALYSIS METHODS (FROM EXPERIENCE OF APPLICATION)
RESEARCH ON THE LEVEL OF STUDENT PERFORMANCE USING MULTIVARIATE ANALYSIS METHODS (FROM EXPERIENCE OF APPLICATION)
Abstract
The article presents a study of the quality of education of students of a pedagogical university by analyzing the performance of students using statistical data of the rating system of knowledge evaluation. An algorithmic approach to the study of learning performance of students on the basis of multivariate analysis is proposed. The algorithm is tested on the statistical information of the rating system of evaluating the knowledge of students in Lipetsk State Pedagogical P.Semenov-Tyan-Shansky University at the bachelor's degree program. The application of cluster analysis methods made it possible to identify non-obvious patterns within the student group. According to the results of the conducted pedagogical research, conclusions are made and recommendations are given about the options to improve the level of achievement of students in higher education institutions.
1. Введение
Актуальным направлением развития образовательной системы сегодня является повышение качества знаний, при этом одним из значимых показателей выступает уровень успеваемости обучающихся, на который оказывают влияние такие факторы как: уровень знаний обучающихся, изменения в учебной программе, методике преподавания дисциплины, переход на дистанционное обучение и др. [1], [2], [4], [17].
Как показывает опыт, практическая значимость педагогического исследования раскрывается вследствие накопления, систематизации, обработки статистических данных, поэтому рекомендации для эффективного формирования результатов обучения носят в своем большинстве вероятностный и интуитивный характер. Систематический мониторинг успеваемости – один из инструментов для принятия своевременных управленческих решений в образовании и корректировке списка факторов, оказывающих влияние на уровень успеваемости обучающихся. Для корректного анализа результатов педагогического исследования, сравнения однотипных показателей за различные периоды и их интерпретации, построения прогноза необходимо использовать методы многомерного анализа. Симбиоз факторного, регрессионного, дисперсионного, кластерного анализов позволяет построить наиболее содержательную модель при проведении педагогического исследования.
Непрекращающиеся реформы российского образования, безусловно, оказывают влияние на качество знаний обучающихся и вызывают повышенный интерес к проблеме исследования факторов, влияющих на данный показатель. В работах [1], [9], [13] построены линейные модели множественной регрессии для прогнозирования успеваемости студентов. В [9] в качестве входных параметров были учтены: оценки экзаменационных сессий студентов по общепрофессиональным или специальным дисциплинам, оценки экзаменационных сессий по обеспечивающим дисциплинам, число обеспечивающих дисциплин. В [1] при построении модели были учтены умение самостоятельно планировать работу в режиме рейтинговой оценки, самооценка владения определенными компетенциями постановки задач самосовершенствования, выполнение индивидуальных заданий. В [13] при моделировании учитывались средний балл ЕГЭ, наличие дополнительных занятий после учебы, место проживания, финансовое положение семьи, «умение использовать знания других», цель обучения, здоровье студента, наличие или отсутствие романтического увлечения.
В [10] рассматриваются методики построения деревьев решений, предназначенных для классификации студентов на основе информации, зафиксированной в личном деле, выделяя из них группу риска, т.е. первокурсников, которые с высокой долей вероятности могут быть отчислены уже по итогам первого учебного цикла.
В [8] показаны целесообразность и возможность применения теории латентных переменных для статистического анализа успеваемости студентов, определено местоположение учебных дисциплин на шкале успеваемость студентов.
В [12] предлагается авторская методика с целью идентификации дисциплин, которые осваиваются студентами с определенными сложностями, при этом осуществляют расчет суммарного балла риска каждой дисциплины и кластеризацию дисциплин.
В [7] рассматривается подход к априорной оценке успеваемости студентов с использованием искусственных нейронных сетей, интерес представляет прогнозирование ожидаемого результата студента и построение оценки на основе использования промежуточных результатов проверки знаний.
Проведенный обзор, ставший теоретической базой исследования, доказывает актуальность педагогической проблемы и необходимость расширения математического инструментария для её решения. В связи с этим целью исследования стала разработка и апробация алгоритмического подхода для исследования успеваемости обучаемых на основе проведения многомерного анализа. Для её реализации были поставлены и решены следующие задачи:
- описание шагов алгоритмического подхода для анализа успеваемости обучаемых на основе использования методов многомерного анализа;
- апробирование разработанного алгоритма в процессе анализа успеваемости одной из студенческих групп в ЛГПУ имени П.П. Семенова-Тян-Шанского.
2. Методы и принципы исследования
Для решения поставленных задач использовались следующие методы исследования: анализ научно-методической литературы, системный подход, методы многомерного анализа.
3. Основные результаты
Проблема неуспеваемости относится к числу вечных, причём неважно, о какой образовательной организации идёт речь, и мотивация обучаемых – одна из основных проблем современного образования. Оценка успеваемости – конечный и один из самых важных этапов процесса обучения и процесса повышения качества обучения. Применение балльно-рейтинговой системы в системе высшего образования РФ позволяет осуществлять комплексный учет успеваемости каждого студента [2].
В рамках педагогического исследования М.Ю. Карловой разработан алгоритмический подход для проведения анализа успеваемости обучаемых по статистическим данным рейтинговой системы оценивания знаний на основе использования методов многомерного анализа (рис.1).

Рисунок 1 - Алгоритм для проведения исследования уровня успеваемости обучаемых по данным балльно-рейтинговой системы
На первом этапе исследования была собрана статистическая информация согласно рейтинговой системе оценивания знаний обучающихся в ЛГПУ им. П.П. Семёнова - Тян - Шанского на бакалавриате «Математика и информатика». При такой системе оценивания успеваемость студентов дифференцируется в гораздо большей степени, чем при пятибалльной системе. Для исследования была сформирована выборка только из студентов, которые составляют группу после сдачи 5 сессий и «не сошли с дистанции» по различным причинам. Выбранная студенческая группа является смешанной: в ней обучаются также будущие педагоги, для которых русский язык не является родным, кроме того, ребята имеют разный уровень школьной подготовки, как показывает практика, преподавать в таких группах дело непростое.
На втором этапе для представления структуры связей между уровнями успеваемости по семестровым данным построили матрицу корреляций, элементы которой наглядно доказывают зависимость успеваемости обучаемых от накопленного опыта при сдачи сессий: все элементы матрицы, кроме уровня успеваемости в пятом семестре, имеют значения больше 0,8, что свидетельствует о наличии мультиколлинеарности, а также о линейной и достаточно тесной связи между оценками с первого по четвёртый семестр (табл. 1).
Таблица 1 - Корреляционная матрица успеваемости
Семестр | 1 | 2 | 3 | 4 | 5 |
1 | 1 | 0,957 | 0,933 | 0,814 | 0,914 |
2 | 0,957 | 1 | 0,943 | 0,852 | 0,960 |
3 | 0,933 | 0,943 | 1 | 0,878 | 0,938 |
4 | 0,814 | 0,852 | 0,878 | 1 | 0,775 |
5 | 0,914 | 0,960 | 0,938 | 0,775 | 1 |
Связь между уровнями успеваемости в четвёрном и пятом семестрах несколько ниже, чем в предыдущих, это объясняется появлением достаточно сложных специальных дисциплин из предметно-методического модуля, таких как «Дифференциальные уравнения», «ИКТ и медиаинформационная грамотность», «Веб - технологии» / «Веб - программирование», «Компьютерные сети и Интернет», «Теория вероятностей и математическая статистика», «Теория функций действительного переменного», «Языки и методы программирования», кроме того ребята писали и защищали курсовую работу по предмету «Языки и методы программирования», готовили отчёты по производственной практике: педагогическая (адаптационная) и учебной практике: ознакомительная (по профилю математика).
Действительно, студенты с течением времени понимают, как нужно готовиться к экзаменам и зачётам, более осмысленно относятся к требованиям педагогов и стараются добросовестно выполнить задания, в том числе и самостоятельно, повышают уровень образованности, применяют знания, полученные на ранних этапах обучения в вузе, учатся правильно распределять усилия при подготовке и стравляться с волнением при прохождении испытаний в рамках учебного процесса. Безусловно, рейтинговая система оценивания является мощным инструментом мотивации для студентов, желающих получать стипендию. Кроме того, в настоящее время за особые успехи в учёбе размер стипендии может быть значительно увеличен.
На третьем этапе, исходя из классического представления об оценивании, данные рейтинга были распределены по 4-м группам: «отлично успевающие», «хорошо успевающие», «удовлетворительно успевающие», «неуспевающие» (табл. 2). Такое распределение позволяет систематизировать исходную информацию по уровню успеваемости в группе и немного прояснить сложившуюся ситуацию. Полученные результаты группировки говорят о мало изменяющемся количестве обучающихся в каждой из сформированных подгрупп на протяжении исследуемого временного промежутка. В пятом семестре существенно увеличилось количество обучаемых, попавших по успеваемости в интервал [86-100]– «отлично успевающие» за счет перехода из интервала [70-85] – «хорошо успевающие».
Таблица 2 - Интервальные значения сдачи сессии в группе
Баллы | Оценка | Семестр | ||||
1 | 2 | 3 | 4 | 5 | ||
Количество студентов | ||||||
[0-49] | 2 | 0 | 0 | 1 | 1 | 0 |
[50-69] | 3 | 11 | 11 | 10 | 10 | 11 |
[70-85] | 4 | 6 | 6 | 5 | 8 | 4 |
[86-100] | 5 | 9 | 9 | 10 | 7 | 11 |
Итого, чел. | 26 | 26 | 26 | 26 | 26 | |
Результат четвёртого этапа педагогического исследования – точечные и интервальные значения базовых статистических показателей, характеризующих средний уровень успеваемости в группе (табл. 3).
Таблица 3 - Значения базовых статистических показателей уровня успеваемости обучаемых
Семестр | Статистические показатели | |||
Точечные оценки | Интервальная оценка | |||
Средний уровень успеваемости в группе – , балл | Среднее квадратическое отклонение успеваемости в группе – , балл | |||
1 | 74,457 | 13,809 | (69,15; 79,77) | (11,05; 19,45) |
2 | 75,136 | 12,555 | (70,31; 79,96) | (10,05; 17,69) |
3 | 74,924 | 15,071 | (69,13; 80,71) | (12,06; 21,23) |
4 | 71,395 | 20,811 | (63,4; 79,39) | (16,65; 29,32) |
5 | 73,987 | 15,169 | (68,16; 79,82) | (12,14; 21,37) |
Из таблицы 3 вытекает, что группа в среднем показывает неплохой уровень успеваемости согласно рейтинговой системе, а именно заслуживает оценку «хорошо». Самый высокий уровень успеваемости обучаемые показали во 2 семестре, но при этом выборку нельзя считать однородной, т.е. студенты с разной «степенью успеха» сдали сессию (отклонение почти в 13 баллов). В 4 семестре отмечен наибольший разброс баллов (отклонение в 21 балл). Достаточно широкие доверительные интервалы, построенные надежность =0,95, также свидетельствуют о разном уровне успеваемости в группе.
На рисунке 2 приведены гистограммы успеваемости по данным бально-рейтинговой системы. Выявленные бимодальность и полимодальность распределений наглядно подтверждают неоднородность выборки в каждом семестре и, следовательно, свидетельствует о разном уроне успеваемости обучаемых в исследуемой группе. С учётом сделанных выводов целесообразно изучить внутреннюю структуру выборки и переформировать подгруппы.
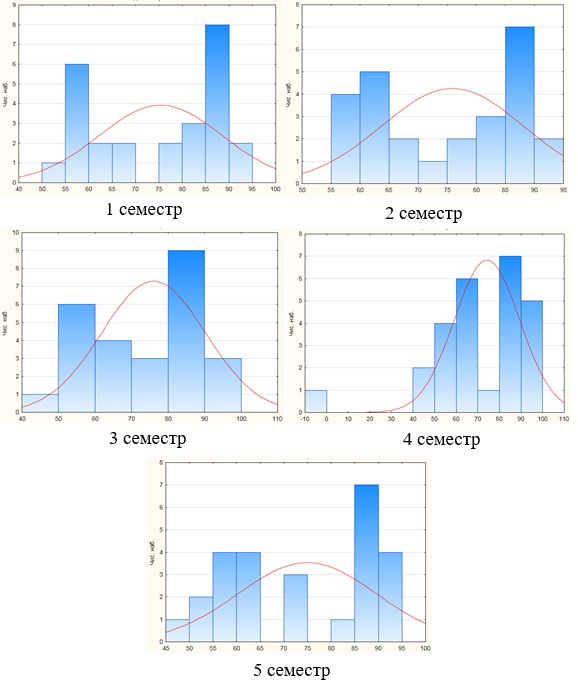
Рисунок 2 - Гистограммы рейтинговой оценки группы
На пятом этапе педагогического исследования для проведения кластеризации использовался пакет прикладных программ Statistica (модуль – кластерный анализ). С помощью метода k-средних кластерного анализа разбили исходные данные, характеризующие рейтинг обучаемых, исходя из классического представления об оценивании, на 4 кластера (табл. 4). В основу разбиения положен следующий принцип: вначале был определён центр кластера (выбраны 4 студента с максимально отличающимся рейтингом), а затем вокруг него сгруппированы все остальные обучаемые в пределах заданного порогового значения (в каждый кластер отбираются студенты с рейтингом достаточно близким к «центровому»).
Таблица 4 - Элементы сформированных согласнометоду k-среднихкластеров и мера различия между уровнями успеваемости в каждом кластере
Кластер | Элементы кластера (номер студента – С_i, i=1,…,26) и расстояние до центра кластера | ||||||||||
1 | C_13 | C_14 | C_15 |
|
|
|
|
|
|
|
|
1,965 | 2,177 | 3,472 |
|
|
|
|
|
|
|
| |
2 | C_5 | C_6 | C_7 | C_8 | C_9 | C_10 | C_11 | C_12 |
|
|
|
2,417 | 2,307 | 1,819 | 2,045 | 0,818 | 1,097 | 2,599 | 4,165 |
|
|
| |
3 | C_1 | C_2 | C_3 | C_4 |
|
|
|
|
|
|
|
1,735 | 2,301 | 1,998 | 2,327 |
|
|
|
|
|
|
| |
4 | C_16 | C_17 | C_18 | C_19 | C_20 | C_21 | C_22 | C_23 | C_24 | C_25 | C_26 |
7,668 | 7,350 | 8,100 | 3,096 | 2,974 | 5,489 | 3,461 | 6,038 | 3,403 | 24,610 | 4,205 | |
Сравнительный анализ данных таблиц 2 и 4 говорит о том, что результаты группировок различны. Таким образом, с помощью метода k-средних удалось сформировать студенческие подгруппы с максимально «схожим» уровнем успеваемости, и в тоже время обучаемые из разных кластеров имеют максимально «отличный» уровень успеваемости.
В таблице 5 приведены евклидовы расстояния между кластерами (расстояния под диагональю, квадраты расстояний над диагональю).
Таблица 5 - Евклидовы расстояния между сформированными кластерами
Кластер | 1 | 2 | 3 | 4 |
1 | 0,000 | 124,420 | 246,560 | 335,897 |
2 | 11,154 | 0,000 | 25,514 | 790,793 |
3 | 15,702 | 5,051 | 0,000 | 1085,385 |
4 | 18,328 | 28,121 | 32,945 | 0,000 |
Расстояния между кластерными центрами указывают, что кластеры разделены достаточно хорошо. Из расчётов вытекает, что уровень успеваемости студентов из четвёртого кластера имеет достаточный разброс по сравнению с другими кластерами, элементы которых расположены достаточно кучно вокруг центра. Наименьшее различие в уровне успеваемости между студентами второго и третьего кластеров, т.е. большая вероятность перехода из одной подгруппы в другую.
Достоинство метода k-средних кластерного анализа – это возможность наглядной интерпретации кластеров с использованиемграфика «Средних значений в кластерах». На рисунке 3 представлены графики средних рейтинговых баллов в каждом кластере, что позволяет сделать вывод о составе каждого кластера и положений кластеров друг относительно друга.
Из визуального представления следует, что в 3 кластер попали «отлично успевающие» (4 студента из 26), во 2 кластер – «хорошо успевающие» (8 студентов из 26), в 1 кластер – «удовлетворительно успевающие» (3 студента из 26), в 4 кластер – «неуспевающие» (11 студентов из 26).
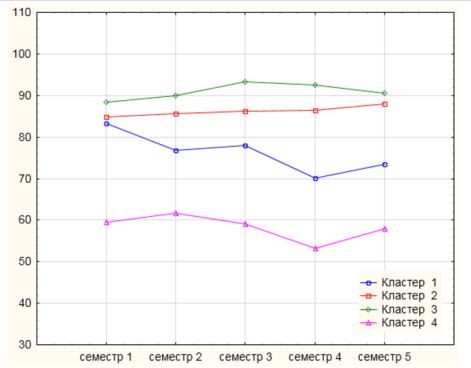
Рисунок 3 - Графики средней рейтинговой оценки в каждом кластере
Расчёт значений описательных статистик в каждом кластере рейтинговой оценки, безусловно, является важным и информативным этапом исследования (табл. 6).
Таблица 6 - Описательные статистики кластеров
Семестр | x ср | сигма | x ср | сигма | x ср | сигма | x ср | сигма |
Кластер 1 | Кластер 2 | Кластер 3 | Кластер 4 | |||||
1 | 83,273 | 4,500 | 84,808 | 2,691 | 88,455 | 3,237 | 59,435 | 5,371 |
2 | 76,730 | 1,800 | 85,584 | 1,737 | 89,968 | 1,337 | 61,710 | 4,048 |
3 | 78,000 | 3,807 | 86,289 | 3,499 | 93,305 | 3,300 | 59,135 | 6,130 |
4 | 70,063 | 3,475 | 86,344 | 2,129 | 92,605 | 0,991 | 53,173 | 18,770 |
5 | 73,557 | 1,253 | 87,965 | 2,202 | 90,537 | 2,319 | 57,921 | 4,475 |
Уровень успеваемости «хорошо успевающих» имеет возрастающую тенденцию, студенты, попавшие во 2 кластер, явно стремятся повысить свой уровень успеваемости и перейти в группу «отлично успевающих». Уровень успеваемости в 3 кластере – «отлично успевающие», начиная с 3 семестра, демонстрирует убывающую динамику. В этой связи можно предположить, что ребята, попавшие в данный кластер, почувствовав себя лидерами, несколько «расслабились» и не стремятся существенно повысить свои баллы. Это нехорошая тенденция, и, возможно, такая практика приведёт к переходу некоторых обучаемых из группы «отлично успевающие» в группу «хорошо успевающих». Средним 1 кластера – «удовлетворительно успевающие»и 4 – «неуспевающие» присущи колебания.
Из данных таблицы 6 вытекает, что наибольший разброс по рейтингу присущ «неуспевающим» в 4 семестре, сложившаяся ситуация указывает на то, что среднему значению (53 балла) просто нельзя доверять в данном случае и о значительной верификации баллов в кластере. Интересно, что минимальный разброс зафиксирован в том же семестре в 3 кластере – «отлично успевающие», что говорит об однородности выборки и очень близком уровне успеваемости студентов, попавшим в 3 кластер. В 4 семестре студенты сдавали следующие предметы: «Архитектура ЭВМ и систем», «Геометрия», «Иностранный язык», «Информатика», «Элективные курсы по физической культуре и спорту», «Математическая логика и теория алгоритмов», «Математический анализ», «Педагогика», «Психология», «Теория функций комплексного переменного», «Философия», кроме того ребята писали и защищали курсовую работу по предмету «Информатика», готовили отчёты по учебным практикам: ознакомительная (по профилю информатика) и ознакомительная (здоровьесберегающая).
Дисперсионный анализ выявил существенное различие в сформированных по методу k-средних кластерах: значение р<0,05 говорит о значимом различии внутри кластеров (табл. 7). Это свидетельствует о том, что у обучаемых в подгруппе (выделенном кластере) есть потенциал как повысить свой уровень успеваемости, так и понизить его.
Таблица 7 - Дисперсионный анализ для определения значимости различия между полученными кластерами
Семестр | Между SS | cc | Внутри SS | cc | F | Значим. p |
1 | 4356,137 | 3 | 411,102 | 22 | 77,706 | 0,000000 |
2 | 3743,592 | 3 | 196,830 | 22 | 139,476 | 0,000000 |
3 | 5155,150 | 3 | 523,174 | 22 | 72,260 | 0,000000 |
4 | 7245,061 | 3 | 3582,077 | 22 | 14,832 | 0,000017 |
5 | 5498,620 | 3 | 253,495 | 22 | 159,069 | 0,000000 |
Как справедливо замечено в [3], деление на «отличников», «троечников», «хорошистов», «двоечников» является условным и свойственное только учебным заведениям. При таком подходе к оцениванию работает критерий, который оценивает, насколько хорошо студент учится и в каком контакте находится с преподавателями, но в профессиональной среде таких критериев нет, здесь в первую очередь обращают на личностные и деловые качества человека (рис. 4). Поэтому для более детального анализа проверили, формируют ли рейтинговые оценки "естественные" кластеры, которые могут быть осмыслены. С этой целью были использованы в качестве правила объединения метод полной связи, в качестве меры близости – евклидово расстояние. Результат древовидной кластеризации – иерархическое дерево (рис. 5).
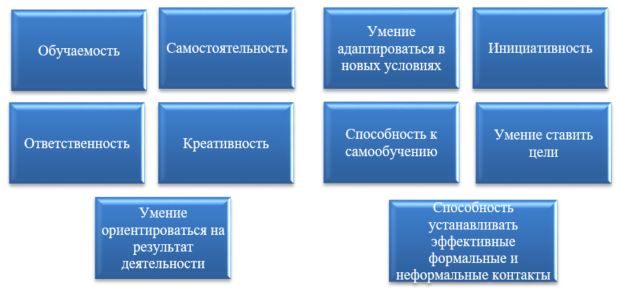
Рисунок 4 - Значимые критерии для профессиональнойсреды
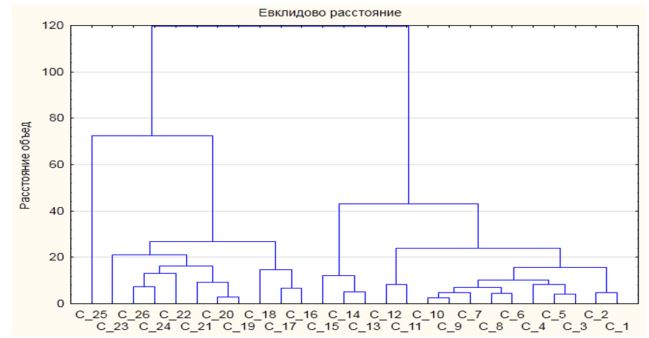
Рисунок 5 - Вертикальная дендрограмма успеваемости обучаемых в группе
Читая диаграмму сверху с рейтинговой оценки каждого студента в своем собственном кластере при смещении вниз проследили объединение и формирование кластеров из обучаемых, которые по успеваемости «теснее соприкасаются друг с другом». Положение узлов на вертикальной оси определяет расстояние, на котором были объединены соответствующие кластеры. На основании схемы объединения согласно методу полной связи сформирована таблица 8, в которую попала первая десятка из обучаемых, имеющих близкий уровень успеваемости.
На шестом этапе, проведя анализ данных таблицы 8, делаем вывод о том, что у группы есть потенциал повысить уровень успеваемости. Этого можно добиться при работе малыми группами, при этом:
- общее задание для C_3 и C_5 позволит повысить индивидуальный уровень успеваемости C_5;
- нецелесообразно давать совместное задание и объединять в пары C_19 и C_20, C_16 и C_17, C_24 и C_26 так как, скорее всего, работа не будет выполнена на должном уровне, лучше каждого из этих обучаемых прикрепить к «более сильному» по успеваемости одногрупнику, который станет «локомотивом» и поможет товарищу лучше разобраться в проблеме и повысить свою успеваемость.
Таблица 8 - Группы студенты с достаточно сходным уровнем успеваемости
№ | Расстояние между объединяемыми в кластер обучаемыми (балл) | Коды студентов | Кластер | Название кластера | ||||
1 | 2,537 | C_9 | C_10 |
|
|
| 2 | «хорошо успевающие» |
2 | 2,861 | C_19 | C_20 |
|
|
| 4 | «неуспевающие» |
3 | 4,272 | C_3 | C_5 |
|
|
| 3+2 | «отлично успевающие» /«хорошо успевающие» |
4 | 4,459 | C_6 | C_8 |
|
|
| 2 | «хорошо успевающие» |
5 | 4,743 | C_1 | C_2 |
|
|
| 3 | «отлично успевающие» |
6 | 4,870 | C_7 | C_9 | C_10 |
|
| 2 | «хорошо успевающие» |
7 | 5,072 | C_13 | C_14 |
|
|
| 1 | «удовлетворительно успевающие» |
8 | 6,820 | C_16 | C_17 |
|
|
| 4 | «неуспевающие» |
9 | 6,931 | C_6 | C_8 | C_7 | C_9 | C_10 | 2 | «хорошо успевающие» |
10 | 7,526 | C_24 | C_26 |
|
|
| 4 | «неуспевающие» |
4. Заключение
Активное включение студентов в процесс разработки и реализации практических инновационных проектов, их участие в различных научно-исследовательских клубах благоприятно скажется на развитии интеллектуального, творческого и делового потенциала будущих педагогов. Интересная проектно-исследовательская деятельность под руководством опытного наставника способна повысить уровень учебно-профессиональной мотивации студентов с различным уровнем успеваемости, создать предпосылки для повышения эффективности подготовки к будущей профессиональной деятельности.
Кроме того, развитие индивидуальных образовательных траекторий в вузе – один из существенных ресурсов повышения уровня качества образования в современных реалиях. Именно при проектировании индивидуальных образовательных траекторий выявляются сильные и слабые стороны студента, возможные пробелы в полученных знаниях, методы и возможности их решения [16].
Нельзя не отметить, что опыт кураторов по адаптации обучаемых позволяет максимально сохранить контингент студентов на первом и последующих курсах, успешно решать вопросы по их обучению и воспитанию, сплотить коллектив и научить ребят взаимопомощи, прививать любовь к выбранной профессии.
В заключение отметим, что систематическая проверка знаний, умений и навыков студентов в процессе их обучения является неотъемлемой составляющей всего учебно-воспитательного процесса, и предложенный алгоритмический подход для проведения исследования уровня успеваемости обучаемых по данным балльно-рейтинговой системы может служить инструментом объективной оценки. Полученные результаты педагогического исследования помогут руководству отрегулировать обучение для повышения качества обучения, помочь преподавателям корректировать свою педагогическую деятельность, что в свою очередь приведёт к улучшению образовательных результатов и повысить уровень успеваемости, как в отдельно взятой группе, так и в целом по вузу.
