MODELLING THE DESCENT AND LANDING OF A QUANTOMOBILE
MODELLING THE DESCENT AND LANDING OF A QUANTOMOBILE
Abstract
The prospect of introducing quantomobiles that use the thrust of a Quantum Propulsion Engine (QPE) implemented in the pitch plane when a Vehicle (V) is moving on the ground and in the air necessitates consideration of the landing characteristics of these machines. The landing of a quantomobile is not a mirror image of its lift. Unlike a lift (with some trajectory dispersion), during landing it is necessary to solve the problem of matching the glide path with the Reference Surface (RS), on which the impact loads of the V depend. In the absence of full-scale vehicles with QPE, the focus is on Software Simulation Modelling (SSM) and a flexible model. The objectives of the research were the following: to create a Procedure for Descent and Landing (PDL) in the author's model of the Quantomobile's Ground Movement (QGM); to develop an interface for interacting with the model; to conduct SSM with experiments covering a number of vehicle landing options. A four-phase algorithm for intensive descent and landing has been implemented in the QGM environment. The algorithm allows the trajectories of movement indicators to be tracked during the SSM of the quantum vehicle landing. The graphical capabilities of Matlab software are used. In a series of calculations of the descent and landing of a quantomobile under various scenarios of changes in the initial values of descent altitude, longitudinal velocity, tilt angles of the thrust vector, and other factors, an assessment of vehicle landing options with QPE is given. For two variants of a hypothetical quantum vehicle, a framework of reference trajectories with maximum intensity for landing has been formed. The developed PDL allows for the study of the descent and landing of a vehicle in the pitch plane, with the possibility of subsequent movement along the SR. Based on the calculations and their analysis, the cognitive complexity of forming the trajectories of the quantum vehicle during its descent and landing in relation to the thrust and aerodynamic lift forces (TLF and ALF) has been overcome. The presence of TLF QPE is a unifying factor in the synthesis of CTOL, STOL and VTOL landing methods, covered by a single algorithm. SSM is regarded as the basis for further development of quantomobile motion modelling in arbitrary conditions.
1. Введение
В развитие идеи извлечения энергии из физического вакуума (ФВ) в физике формируется единая теория пoля — суперобъединения гравитационных и электромагнитных сил, — которая послужила бы научной платформой для практического извлечения энергии. Примерами конкурирующих вариантов этой теории могут служить GEM (Gravity-Electro-Magnetism) Unification Theory Д. Бранденбурга и Теория Суперобъединения Леонова В. С. .
Одной из целей теории суперобъединения является реализация механизма осуществления пропульсии (формирования траста – толкающей силы). Можно отметить успехи группы Д. Бранденбурга по созданию Теории пропульсии . Однако до завершения этой работы еще неблизкий путь. Одно из обстоятельств этого — малость практических наработок в этой области.
Всё же достигнутый уровень знаний позволяет прогнозировать осуществление идеи бестопливного квантового двигателя (КД), реализующего пропульсию в ФВ путем местной деформации грави-электро-магнитного поля c получением опоры трасту со стороны внешнего ареала поля (во исполнение 3-го закона Ньютона).
Над этой идеей работают научные коллективы, в основном, в космической отрасли — поскольку уровень энергообеспечения ракетоносителей близок к потолку и внедрение бестопливной энергетики предельно актуально. Несколько публикаций, свидетельствующих об этом: США , , ; Великобритании , ; Германии ; Китае ; России , . Освоение бестопливной энергетики на обозначенных принципах затронет все сферы мирового производства — и к этому надо готовиться.
На вопрос о возможности внедрения КД в сфере автомобильного транспорта в NASA утверждают утвердительно . Тесты, проводимые НАСА и другими организациями, доказывают, что КД создает траст и в вакууме, и в атмосфере. Это означает, что КД мог бы заменить другие формы продольной тяги, используемые в традиционных автомобилях. А кроме того, добавить функционал вертикальной тяги.
Наличие вертикальной тяги позволило бы транспортному средству (ТС) висеть и/или двигаться со сменой высоты. Однако пока цена вертикальной тяги (отношение затрачиваемой мощности к создаваемой тяге) — пока высока.
Проблемным (в сравнении с ракетой) в NASA считают обеспечение регулярного эксплуатационного торможения вывешенного ТС. С другой стороны, при наличии управляемой вертикальной тяги вождение упростилось бы и пилоты распрощались бы с ухабистыми взлетами и посадками .
Если коснуться публикаций по летающим автомобилям, то речь будет идти о другом феномене, не соответствующем объекту настоящего исследования. Комплекс двигатель-движитель использует в этих ТС запасенное топливо; он не является объектом бестопливной энергетики. Публикаций же по ТС с бестопливными КДД пока нет. Настоящее исследование можно отнести к актуальным и научно значимым концептам с дальним временным лагом.
Реализация идеи КД приведет к появлению нового типа ТС — квантомобилей , . Станет возможным прикладывать траст КД к корпусу экипажа непосредственно (без трансмиссии). Необходимость трансмиссии отпадет, колесам (при наземном движении) останется только опорная функция.
При возможности шарнирного обметания вектора траста появляется его вертикальная компонента, которую можно будет использовать для управления вертикальным движением квантомобиля. Горизонтальная компонента траста при этом остается для преодоления сил сопротивления продольному движению экипажа (здесь и далее используем слово «экипаж» в смысле «коляска», но не «команда»). КД, с реализацией таким образом функций движителя ТС, становится силовой установкой типа Квантовый двигатель-движитель (КДД). В этой статье ограничимся рассмотрением действий КДД и экипажа в целом только в продольной плоскости тангажа.
Автор ранее рассматривал концепции механики ТС с КДД , . Эти концепции охватывали, в том числе, возможность моделирования всесредного мультимодального квантомобиля (ВМК) . Концепция ВМК содержит 10 уровней режимов движения ТС (от квантолета до квантомарины), 4 из которых затрагиваются в настоящей статье:
1) продольно-вертикальное движение вывешенного ТС в воздухе;
2) продольное граничное (начальное касание опорными элементами границы сред воздух-земля);
3) продольно-вертикальное с частичной опорой на опорную поверхность (ОП);
4) продольное не вывешенное.
Первые два варианта осуществляются только в воздухе — и в этой среде реализуется спуск экипажа. Вторые два варианта осуществляются в комбинации сред воздух-земля — здесь реализуется собственно приземление (пробег) ТС.
В плоскости развёртывания угла тангажа β вектор траста FT раскладывается на две ортогональные компоненты FTx и FTz :
В скалярной записи это:
Затронутые концепции находятся в основе развиваемой авторской Simulink-модели приземного движения квантомобиля (МПДК) .
В публикациях , на базе МПДК рассмотрена методика и даны примеры расчета тяговых сил квантомобилей для наземной среды движения с возможным переходом в воздушную среду. Показывается, что расчетная методика, в связи с необходимостью учета лифта, отличается от традиционных алгоритмов расчета силового баланса автомобиля.
В работах , рассматривались вопросы продольной устойчивости квантомобиля. Подтверждалось, что если для чисто наземного режима движения №4 ВМК эксплуатационные опрокидывающие силовые моменты не представляют опасности (поскольку нейтрализуются взаимодействием экипажа и ОП), то для режимов №№ 1–3 эти моменты опасны (и требуют оперативной нейтрализации — в виде генерации встречных стабилизирующих моментов Mst). Это особенно важно при спуске для режимов 2 и 3, когда требуется зануление угла тангажа (во избежание «козления» экипажа ).
Полет объекта становится возможным только тогда, когда суммарная подъёмная сила (СПС) FzSum, представляющая собой сумму аэродинамической Fwz и трастовой FTz подъемных сил (АПС и ТПС) , превосходит вес этого объекта.
Задача выполнения уверенной посадки летательных аппаратов (ЛА) в процессе развития авиации была одной из проблемных. Автоматическая система посадки космического корабля «Буран» считается уникальным достижением. Курсо-глиссадные и навигационные спутниковые системы посадки ЛА пока остаются автоматизированными . Роль оператора остается центральной, и наработка опыта оптимизации процесса посадки ЛА является необходимой. Для гипотетического объекта — ВМК — траекторная проработка посадки тем более необходима. И эта необходимость усиливается в свете перспектив беспилотной транспортной техники.
В авиации наработан опыт взлета и посадки ЛА, условно разделяющий множество вариантов посадки на три категории: обычная посадка с нефорсированным торможением при пробеге по ОП (Conventional Take-Off and Landing (CTOL)), посадка с форсированно коротким пробегом (Short Take-Off and Landing (STOL)), вертикальная (посадка (Vertical Take-Off and Landing (VTOL)) , . В основе пробега CTOL находится АПС крыльев и фюзеляжа (для вертолета — еще и вертикальная ТПС винта). Для реализации STOL к АПС, как правило, подключаются силы вспомогательных средств создания дополнительной вертикальной тяги. Реализация посадки VTOL производится почти без участия АПС — за счет ТПС одного или нескольких трастеров (если не считать граунд-эффект близости земли , , , у вертолетов и экранопланов , а также сопротивление воздуха вертикальному движению ЛА).
Универсальной схемы, алгоритма посадки существующих ЛА нет. В связи с этим возникает гипотеза: с внедрением в конструкцию ТС квантового двигателя моделирование посадки экипажа станет возможным по единому алгоритму, охватывающему все категории посадки — CTOL, STOL и VTOL.
Кроме верификации этой гипотезы предстоит также оценить динамику сопутствующих процессов — учет упругих сил и демпфирования в подвеске экипажа является важным. При этом, в дополнение к каноническому моделированию колебательного процесса подвески автомобиля, требует рассмотрения и моделирования процесс подхода колес к ОП; выдвижение подвески из корпуса с убором оперения; связанное с этим изменение конфигурации и аэродинамики экипажа и др. Сконцентрировав внимание на этом технологическом аспекте и допустив, что колебание неподрессоренных масс у квантомобиля оказывает незначительное влияние на перемещение подрессоренных масс, колебательную систему подвески представили в МПДК в самом упрощенном виде: одномассовая колебательная система под нагрузкой с одной приведенной жесткостью (упругостью) cup подвески в целом и одним общим приведенным коэффициентом демпфирования амортизаторов kam, приложенным к общей массе экипажа m , , .
Будем характеризовать нулевым значением вертикальной координаты pz = 0 исходное положение статического равновесия экипажа, когда СПС FzSum = 0 и на экипаж снизу действует лишь сила упругости Fup= Gq =m*g . Унаследуем из работы следующие значения высоты pz (как обобщенные для произвольного комбинированного движения по маршруту): Hlf1 — высота положения экипажа в момент потери (или приобретения) контакта колес с ОП; Hlf2 — высота смены конфигурации (трансформация подвески и оперения); Hlf3 — высота безопасности полета.
Вертикальное движение экипажа в начальный момент касания колес ОП при спуске (на высоте Hlf1) сопровождается квазирезонансным ударом . Фронт нагрузки является линейно возрастающим со стороны рессор и прямоугольно-импульсным со стороны амортизаторов . Для смягчения ударов со стороны амортизатора в МПДК используем экспоненциальный вариант конструктивного смягчения , . Другое средство смягчения удара носит траекторный характер — необходимо в процессе спуска при приближении колес к ОП выводить значения вертикальной скорости vz и ускорения az поелику возможно к нулю.
В связи с тем, что целью рядового приземления квантомобиля на маршруте следования может являться не только (и не столько) посадка на место стоянки, но также (и скорее всего) непосредственно следующее дальнейшее движение по маршруту, будем использовать вместо принятого в авиации термина «посадка» словосочетание «спуск и приземление». При этом к спуску относится фаза движения в воздухе до момента касания опорными колесами ОП, а приземление включает в себя движение с участием колес от точки первоначального касания их ОП до включения режима последующего движения экипажа — либо до остановки его, либо до начала последующего установившегося движения или разгона.
Проработки актуальных вопросов функционирования гипотетического квантомобиля, затронутых в приведенных авторских работах ÷ , ввиду отсутствия подобных опубликованных научных работ других исследователей, можно считать как значимыми, так и опорными для исследования, представляемого в настоящей статье.
2. Методы и принципы исследования
2.1. Цель и задачи исследования
Целью расчетного исследования явилось формирование модели спуска и приземления квантомобиля с обеспечением возможности количественной оценки динамики сопутствующих процессов.
Отсутствие признанных теоретических основ движения квантомобиля, натурных образцов исследуемых объектов и эмпирических данных по ним, вызывает необходимость использовать подход с опорой на программное имитационное моделирование (ПИМ).
Задачами по достижению цели являются следующие:
А. Модернизация модели движения квантомобиля под поставленную цель.
Б. Осуществление в авторской Simulink-модели приземного движения квантомобиля (МПДК) Процедуры спуска и приземления (ПСП) с прослеживанием последовательности этапов движения по реперным высотным точкам:
1) спуск с некой начальной высоты pz0 до высоты безопасности полета Hlf3;
2) дальнейший спуск до высоты выпуска подвески и убирания оперения Hlf2;
3) дальнейший спуск экипажа до высоты касания колес с ОП Hlf1;
4) завершающее динамическое опускание с работой подвески до зануления ТПС (FTz = 0).
В. Отработка интерфейса взаимодействия с моделью, задания сценариев спуска и приземления, контроля движения экипажа, многофакторного вывода результатов.
Г. Проведение ПИМ на базе Simulink-модели с экспериментами, охватывающими некоторое множество вариантов спуска и приземления ТС.
Д. Обсуждение и обобщение результатов расчетов.
Е. Формирование выводов и рекомендаций.
2.2. Балансы сил и моментов в МПДК
Используем 3-DOF (3 degrees of freedom ) Модель приземного движения квантомобиля (МПДК) , – учитываем балансы горизонтальных сил, вертикальных сил и моментов сил.
Баланс горизонтальных сил, действующих на квантомобиль :
где Fr — сила сопротивления качению опорных колес, Н;
Fwx — сила сопротивления воздуха продольному движению, Н;
Fax — продольная сила инерции экипажа, Н;
Gq' — сила давления экипажа на ОП с учетом частичного лифта, Н;
fk0 — коэффициент сопротивления качению колес при нулевой скорости;
fkv — скоростной коэффициент сопротивления качению колес, с2/м2;
Vq — скорость продольного движения квантомобиля, м/с;
cd — коэффициент продольного аэродинамического сопротивления;
ρw — плотность воздуха, Н ×с2/м4;
Sfr — фронтальная площадь экипажа, м2;
Gq — сила тяжести квантомобиля (Gq = m·g), Н;
g — ускорение свободного падения, м/с2;
ax — продольное ускорение экипажа, м/с2;
δwh — коэффициент инерции вращения опорных колес экипажа.
Сила Gq' = Gq – (FTz+Fwz) = Gq – FzSum, где Fwz – АПС, а FzSum – СПС. Приведенная масса m’ = Gq(1+δwh)/g учитывает вращение только колес (трансмиссия отсутствует). Феномен проскальзывания колес не учитывается.
Баланс вертикальных сил :
где Fup(z) — сила упругости подвески;
Fам(vz) — сила сопротивления амортизаторов подвески;
Fvpl(vz2) — сила воздушного сопротивления вертикальному движению экипажа (с учетом площади в плане Spl);
Faz(az) — сила инерции, возникающая при вертикальном ускорении az.
Сила, идущая на вертикальное ускорение экипажа:
Faz(az) = FzSum – Fpz – Fам(vz) – Fvpl(vz2) = FzSum – Fpz – Fvz, (5)
где Fpz = z·cup (cup — приведенный коэффициент упругости подвески, Н/м);
Fvz = Fам(vz) + Fvpl(vz2) — совокупность сил, связанных со скоростью вертикального движения экипажа.
В форме ДУ это:
где: kam — приведенный коэффициент демпфирования амортизаторов подвески, Н·с/м;
kwv = cdv ·(ρw/2)·Spl — фактор вертикальной обтекаемости экипажа, Н·с2м–2;
cdv — аэродинамический коэффициент сопротивления вертикальному перемещению экипажа;
Spl — площадь в плане экипажа, м2.
Детали баланса вертикальных сил можно почерпнуть в работе .
При наличии двух (или более) конфигураций экипажа величѝны cdv и Spl индексируем, например, для исходной конфигурации 1 (для высот 0 ≤ z ≤ Hlf2) – cdv1 и Spl1, а для лётной конфигурации с высотой z > Hlf2 – cdv2 и Spl2. Упрощаем физику процессов: смену конфигурации считаем мгновенной.
В момент перехода с этапа 3 к этапу 4 (начало работы опорных колес) включаются в работу рессоры и амортизаторы. Если рессоры плавно (линейно) воспринимают весовую нагрузку экипажа, то амортизаторы требуют смягчения их силы сопротивления в начале хода штока, особенно при высокой вертикальной скорости vz спускающегося экипажа. Для устранения ступенчатого изменения силы сопротивления в МПДК встроен Модуль формирования снижения сопротивления амортизатора вблизи конечной точки хода штока — посредством реализации Экспоненциального сигмоида , :
Баланс моментов сил представлен на базе схемы рис. 1 (усовершенствованной относительно ). Для режимов движения №№ 1 и 2 схема упрощается по причине исчезновения сил Rz1, Ff1, Rz2, Ff2 и моментов Tf1, Tf2.
Баланс моментов сил относительно точки B (на рис. 1) детально рассмотрен в работе . Основное уравнение (при бездействующих стабилизирующих трастерах):
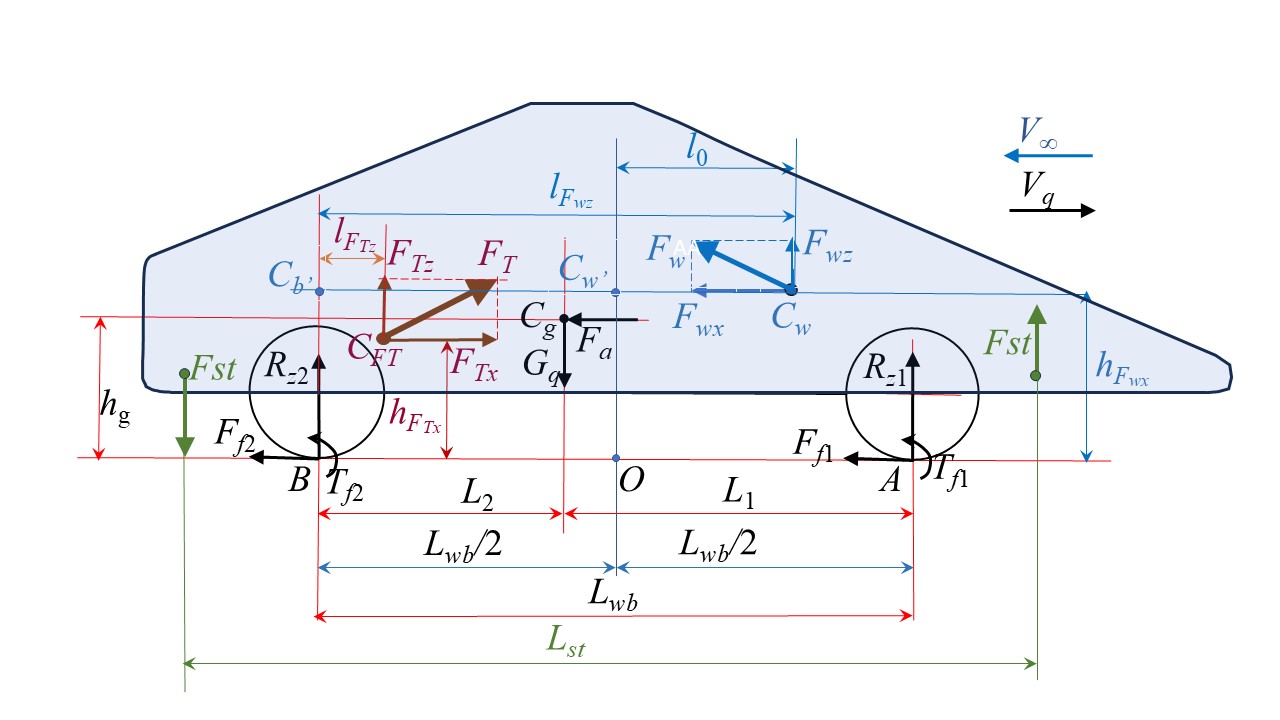
Рисунок 1 - Схема сил, формирующих балансы сил и моментов:
Vq — вектор скорости движения квантомобиля; V∞ — скорость невозмущенного набегающего потока воздуха (|Vq| = |V∞|); Cg — центр тяжести (ЦТ) экипажа; Gq — сила тяжести экипажа; Fa — приведенная сила инерции экипажа; CFT — точка приложения траста КД к корпусу экипажа; FT, FTx и FTz — сила тяги КД (траст) и ее покоординатные компоненты; Cw — центр давления (ЦД) аэродинамических сил; Fw, Fwx и Fwz – сила воздействия воздуха и ее покоординатные компоненты; Ff1 и Ff2 – силы сопротивления качению передних и задних колес, соответственно; Tf1 и Tf2 — моменты сопротивления качению колес; hFwx, hFTx, hg — расстояния векторов соответствующих сил Fwx, FTx, Fa от ОП; lFwz, lFTz — расстояния векторов соответствующих сил Fwz, FTz до вертикали от оси задних колес; l0 – расстояние вектора силы Fwz до вертикали центра колесной базы; Lwb, L1 и L2 – расстояния базовое и от осей колес до проекции центра тяжести на ОП; A и B — центральные точки пятен контакта колес с ОП; Rz1 и Rz2 — нормальные реакции ОП; Lst — расстояние между стабилизирующими трастерами
Примечание: по ист. [19]
При реализации ТСМ двумя дополнительными стабилизирующими трастерами, установленными на расстоянии Lst друг от друга (один на передке, другой на корме – см. рис. 1), требуемая тяга каждого из них:
2.3. Алгоритм максимально интенсивной ПСП
Любой спуск и приземление будут проходить через реперные высотные точки pz0, Hlf3, Hlf2, Hlf1. Однако множество приемлемых траекторий ограничено необходимостью соблюдать условие допустимости ускорений |az(t)| < aдоп.
Построим алгоритм управления и реализации движения модели экипажа для формирования границы множества интенсивных спусков с ограничением по ударному ускорению экипажа (например, |az(t)| < 10 м2). При этом, во-первых, допускаем кратковременное падение (снижение под собственным весом) экипажа с подхватом его ПТС FTz после этого, а во-вторых, минимизируем неизбежный удар при переходе колес из воздуха на ОП. Характеризуем процесс фазами управления вектором траста FT (без требования совпадения их с реперными высотными точками).
Фаза I — Кратковременное падение. В начальной точке экипаж, поддерживаемый силой FTz = Gq (например, 88 кН), находится в вывешенном состоянии на высоте pz0 (например, 200 м), имея начальную продольную скорость Vx0. В момент времени t0 снимается поддержка экипажа до величины FTz = (0 ÷ 0,5)*Gq в виде прямоугольного (либо крутофронтального, например, в пределах 1 с) отрицательного импульса. На второй-третьей секундах восстанавливается поддержка уже до уровня FTzmax (например, 90 кН).
Фаза II — Нейтрализация падения. В отрезке времени до снижения на высоту ≈Hfl2 (например, ≈10 м)_поддерживается уровень FTzmax. Этим самым силой, равной ΔFTz = (FTzmax – Gq), в течение названного времени нейтрализуется (частично) отрицательный импульс силы, приобретенный в фазе I.
Фаза III — Выполаживание глиссады. С использованием гибкого управления величиной траста производится подвод колес к точке касания с ОП на высоте Hfl1 (например, pz = 0,147 м) с наименьшим углом к горизонтали.
Фаза IV — Работа подвески. Гашение неизбежных колебаний экипажа с достижением величины FTz = 0.
Управление трастом FT на краеугольных переходах между фазами может быть сценарно сглажено.
2.4. Программное обеспечение модели МПДК
Структура имитационной системы представлена на рис. 2. Она состоит из пяти подсистем: Vectored_Thrust — для выработки сценариев реализации во времени задающего вектора FT(t) и угла β(t); Longitudinal Dynamics — расчета показателей динамики продольного движения экипажа; Reactions&Moments — расчета силовых моментов в плоскости тангажа ; Vertical Dynamics — динамики вертикального движения экипажа (см. рис. 3); Energetics — расчета показателей энергетики движения (в настоящей статье не используется).
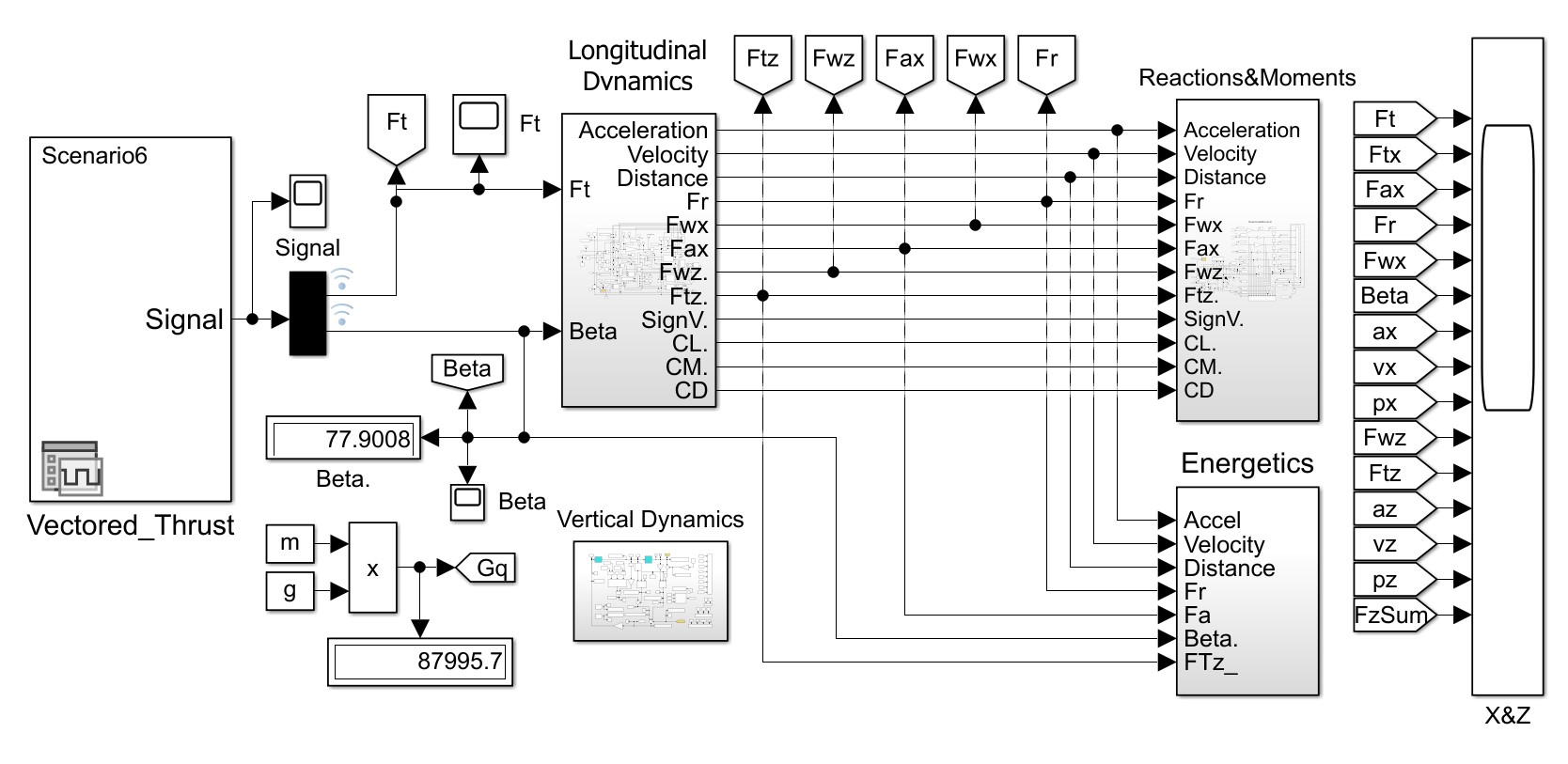
Рисунок 2 - Главный модуль S-модели МПДК
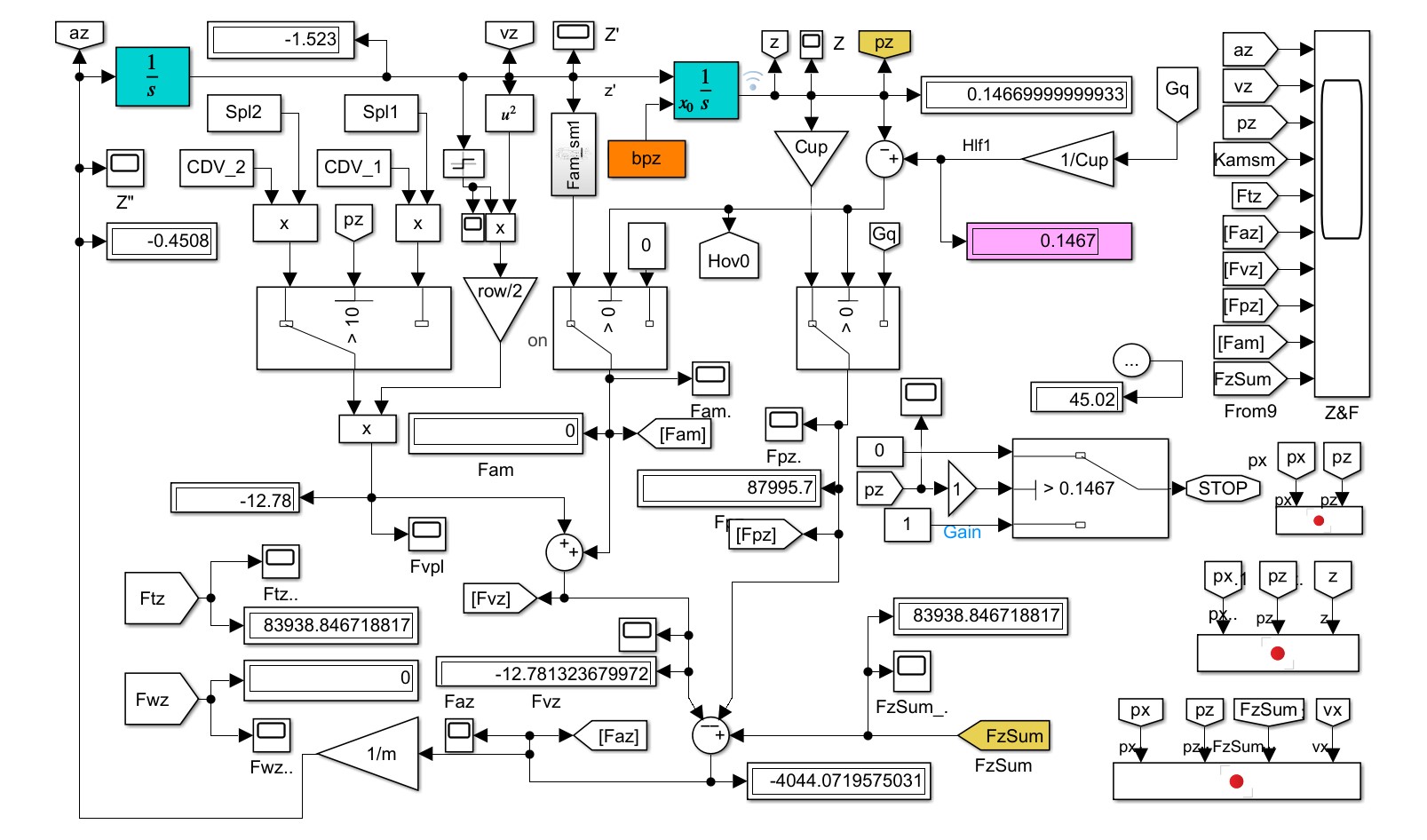
Рисунок 3 - Модуль вертикальной динамики квантомобиля Vertical Dynamics
3. Результаты расчета показателей спуска и приземления экипажа
3.1. Подготовка моделей квантомобилей
Для отработки ПСП, а затем проведения ПИМ спуска и приземления квантомобиля привлекли две крайних макромодели из ряда «плохообтекаемых тел» (ПОТ) (bluff bodies) , : 1-Box и Davis (ранее использованных автором в работах , ). ПОТ 1-Box (с габаритами грузовика КамАЗ-4326), с низкими аэродинамическими свойствами (cd = 0,5; cl = 0 — т.е. с отсутствием АПС), в крайне тяжелых дорожных условиях завершающего пробега (fk0 = 0,3). ПОТ Davis с превосходной аэродинамикой (cd = 0,263; cl = 0,42 – т.е. со значительной АПС) в крайне легких условиях горизонтальной ОП (fk0 = 0,02). Профили этих ПОТ представлены на рис. 4.
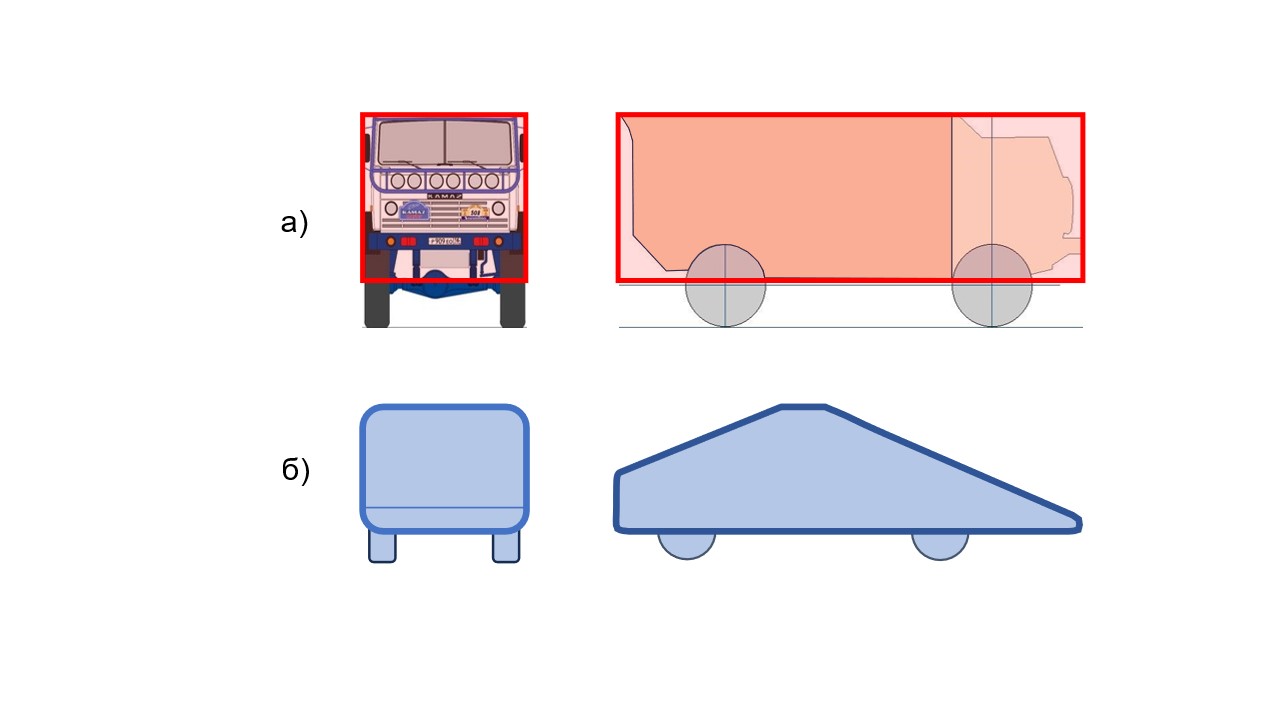
Рисунок 4 - Профили моделей ПОТ:
а - 1-Box; б - Davis
Примечание: по ист. [19]
Таблица 1 - Основные данные по моделям 1-Box и Davis
Параметр | 1 | 2 |
1-Box | Davis | |
L, м | 7,3 | 7,3 |
W, м | 2,55 | 2,55 |
H, м | 3,3 | 1,87 |
Sfr1, м2 | 8,5 | 4,76 |
Sfr2, м2 | 7,5 | 5,5 |
Lwb, м | 4,25 | 4,87 |
L2, м | 2,125 | 2,435 |
Hg, м | 1,3 | 0,9 |
Hw, м | 1,46 | 1,0 |
rd, м | 0,5 | 0,5 |
m, кг | 8970 | 8970 |
Gq, Н | 87995,7 | 87995,7 |
FT, Н | 90000 | 90000 |
cd1 | 0,5 | 0,263 |
cd2 | 0,4 | 0,25 |
cl1 | 0,0 | 0,42 |
cl2 | 0,05 | 0,35 |
cm1 | 0 | –0,35 |
cm2 | 0,1 | –0,2 |
cdv1 | 0,8 | 0,6 |
cdv2 | 0,7 | 0,5 |
Spl1, м2 | 18 | 15 |
Spl2, м2 | 24 | 24 |
fk0 | 0,3 | 0,02 |
fkv, с2/м2 | 0,00037 | 0,00037 |
ЦТ обеих моделей расположили в их срединных плоскостях колесной базы (L2=Lwb/2, где Lwb — колесная база, а L2 — расстояние от ЦТ до вертикальной плоскости задней оси). Точку приложения траста расположили в ЦТ.
В целях возможности продольного движения экипажа весом 88 кН при его полном вывешивании выбрали траст FT = 90 кН (обосновано в ).
Определили значения: высоты спуска pz0 = 200 м; Hlf3 = 25 м; Hlf2 = 10 м; Hlf1 = Gq/cup = 88000 H / 600000 H·м–1 = 0,1467 м.
3.2. Вертикальный спуск ПОТ Davis (при β = 90° и Vx0 = 0 м/с)
Графики рис. 5 – рис. 15 отражают реализации ПИМ по ПОТ Davis.
На рис. 5 приведены временные графики перемещения: по горизонтали – px(t) (экспозиция а)), по вертикали – pz(t) (б)), а также позиционный график pz(px) (в)).
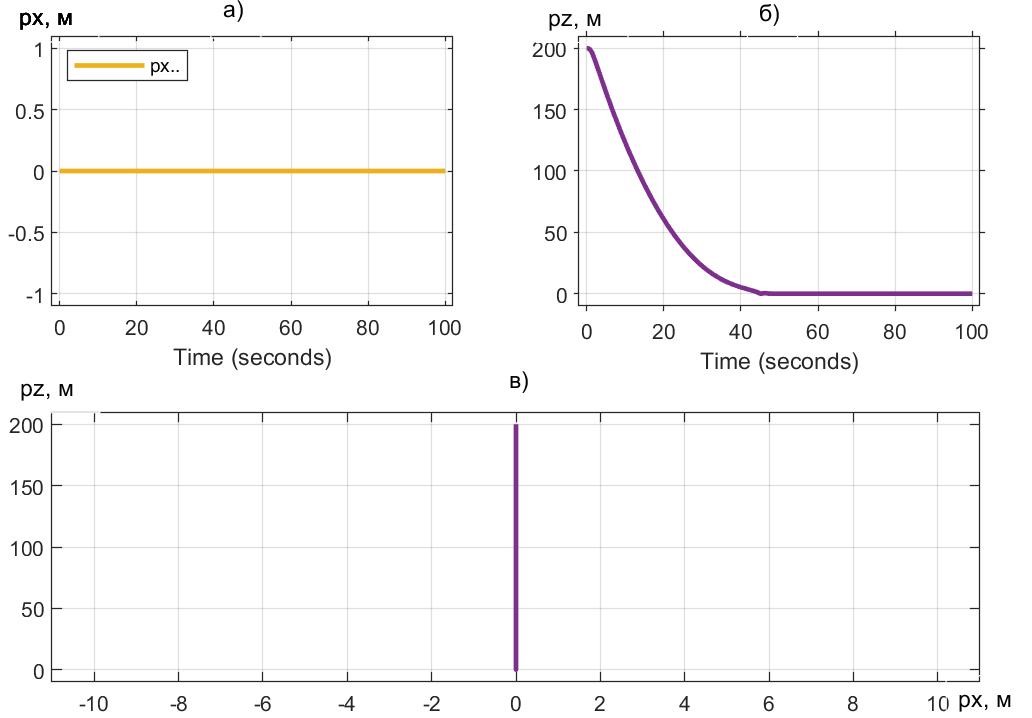
Рисунок 5 - Перемещение модели Davis в процессе вертикальной посадки при Vx0 = 0 м/с
Примечание: под воздействием траста FT = 90 кН и β = 90°
Рисунок 6 - Совокупность показателей процесса вертикального спуска ПОТ Davis c высоты pz0 =200 м
Примечание: FT = 90 кН, β = 90°
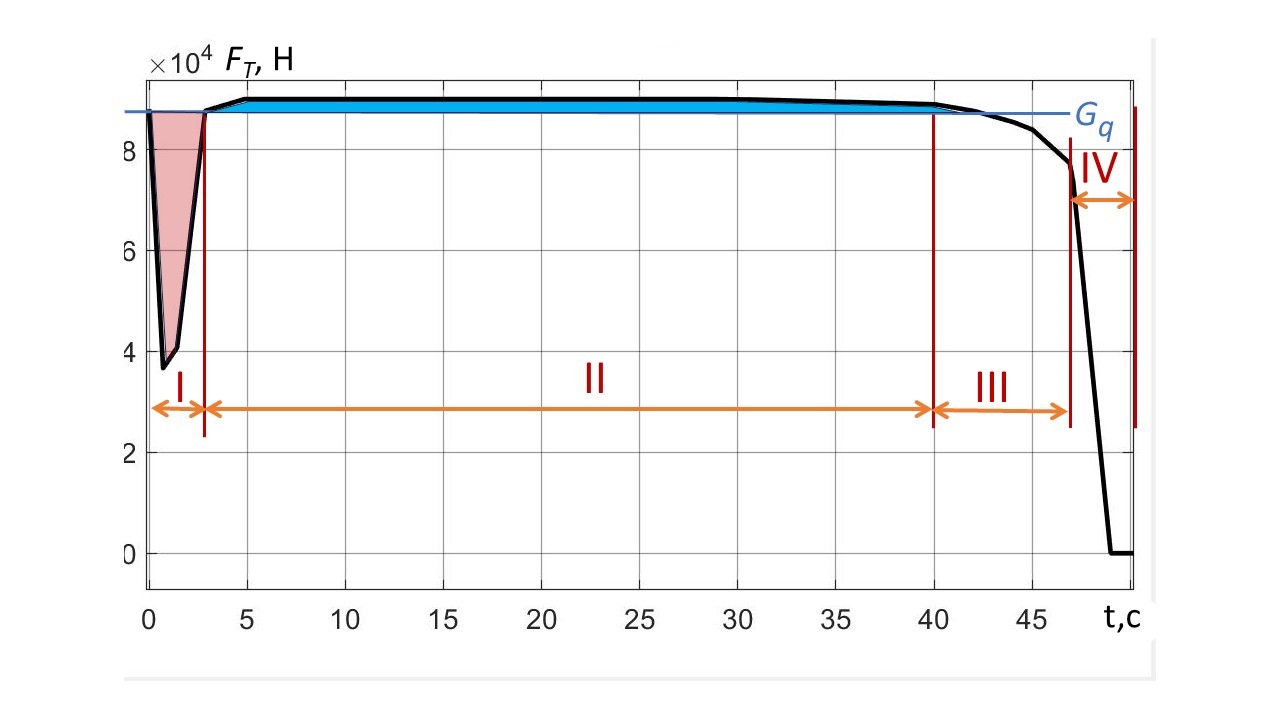
Рисунок 7 - Реализация во времени (t, c) задающего вектора траста FT (H) для интенсивного вертикального спуска ПОТ Davis c высоты pz0 = 200 м
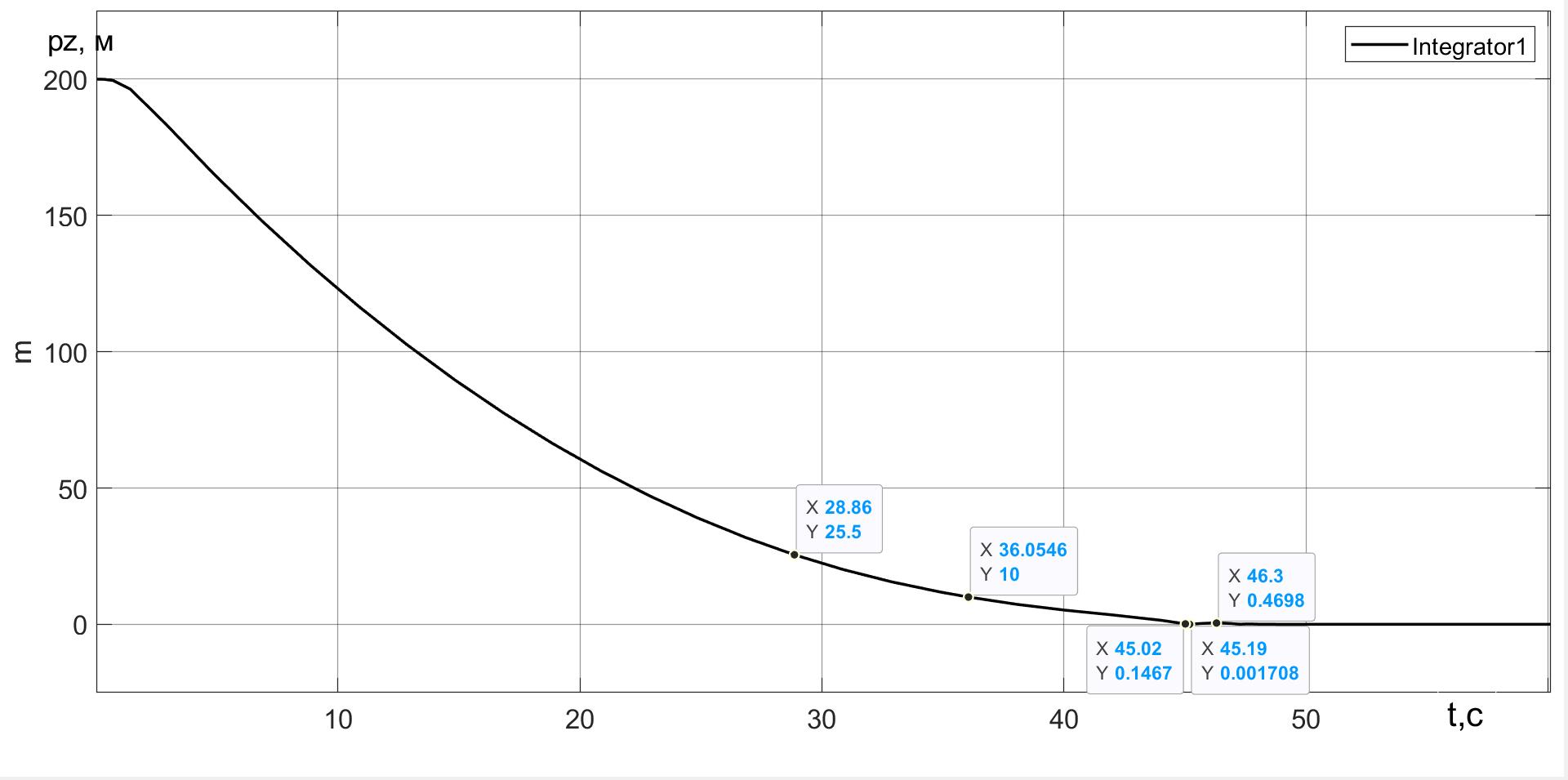
Рисунок 8 - Перемещение pz ПОТ Davis в процессе вертикальной посадки
Примечание: FT = 90 кН, β = 90°
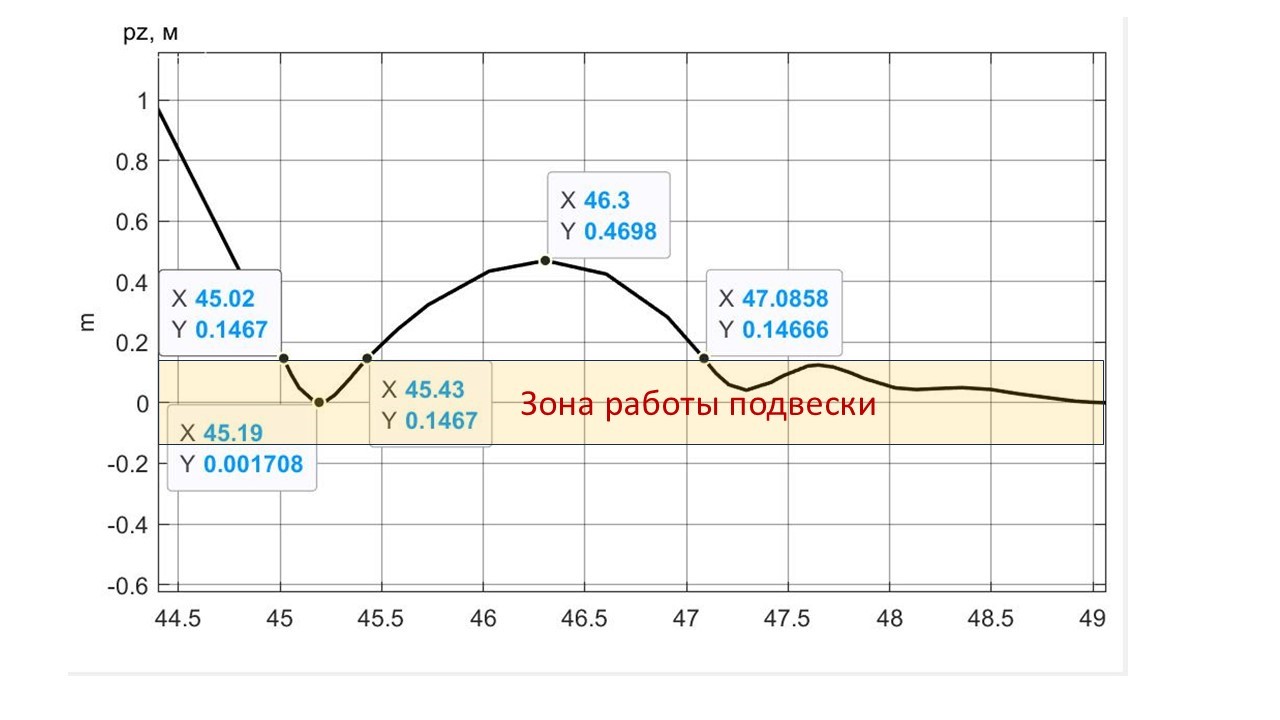
Рисунок 9 - Вертикальное движение ПОТ Davis в процессе вертикальной посадки в зоне касания колесами ОП
Примечание: FT = 90 кН, β = 90° в фазе IV ПСП
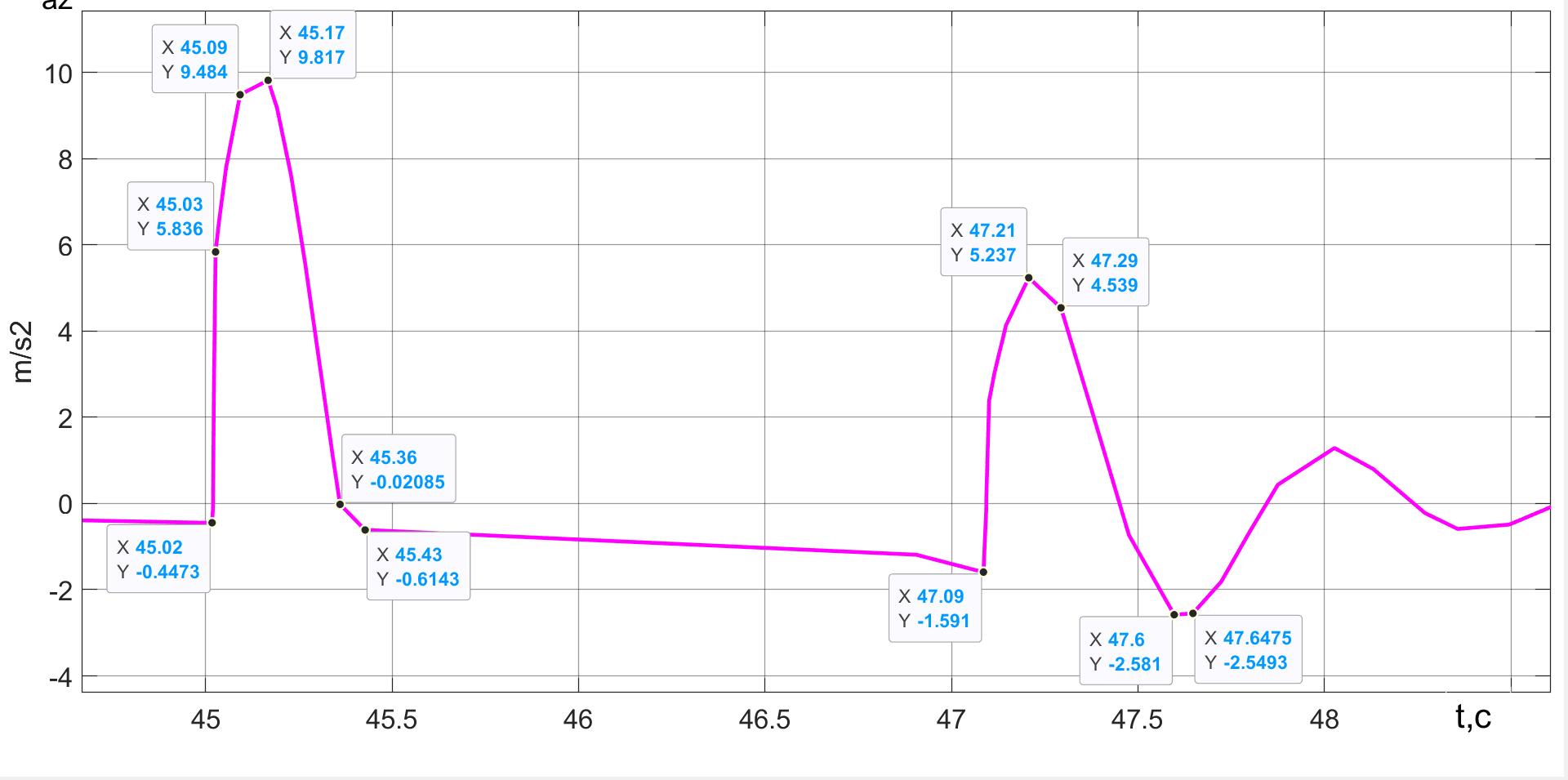
Рисунок 10 - Вертикальные ускорения ПОТ Davis в процессе вертикальной посадки в зоне касания колесами ОП
Примечание: FT = 90 кН, β = 90° в фазе IV ПСП
Графики перемещения ПОТ Davis при вертикальном трасте и начальной продольной скорости Vx0 = 60 м/с приведен на рис. 11.
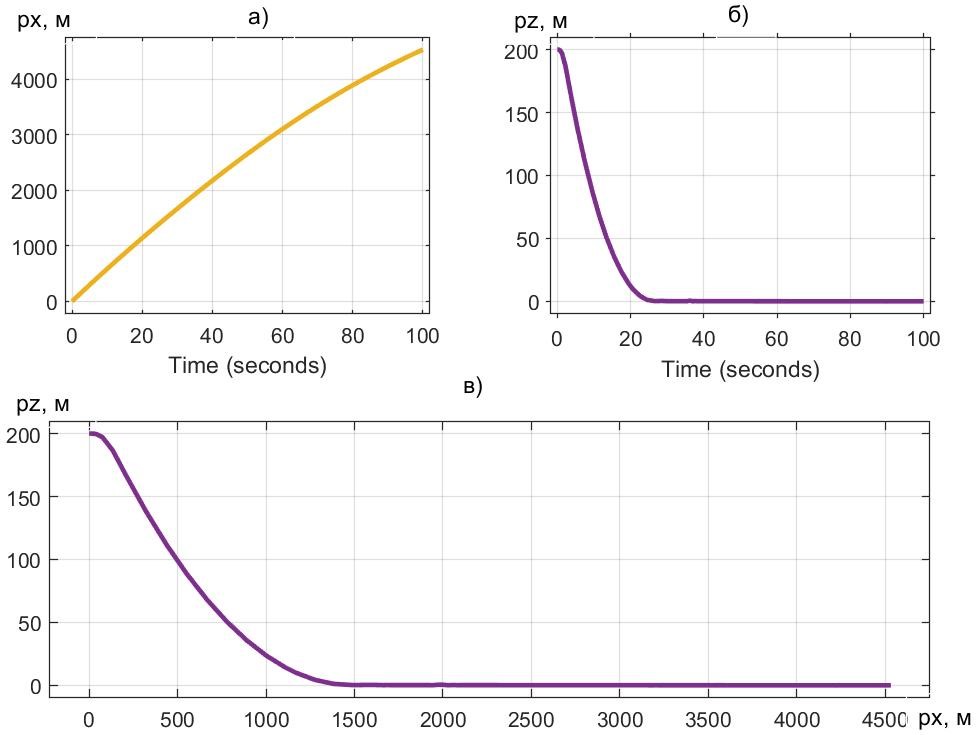
Рисунок 11 - Перемещение модели Davis при начальной скорости Vx0 = 60 м/с под воздействием траста FT = 90 кН и β = 90°
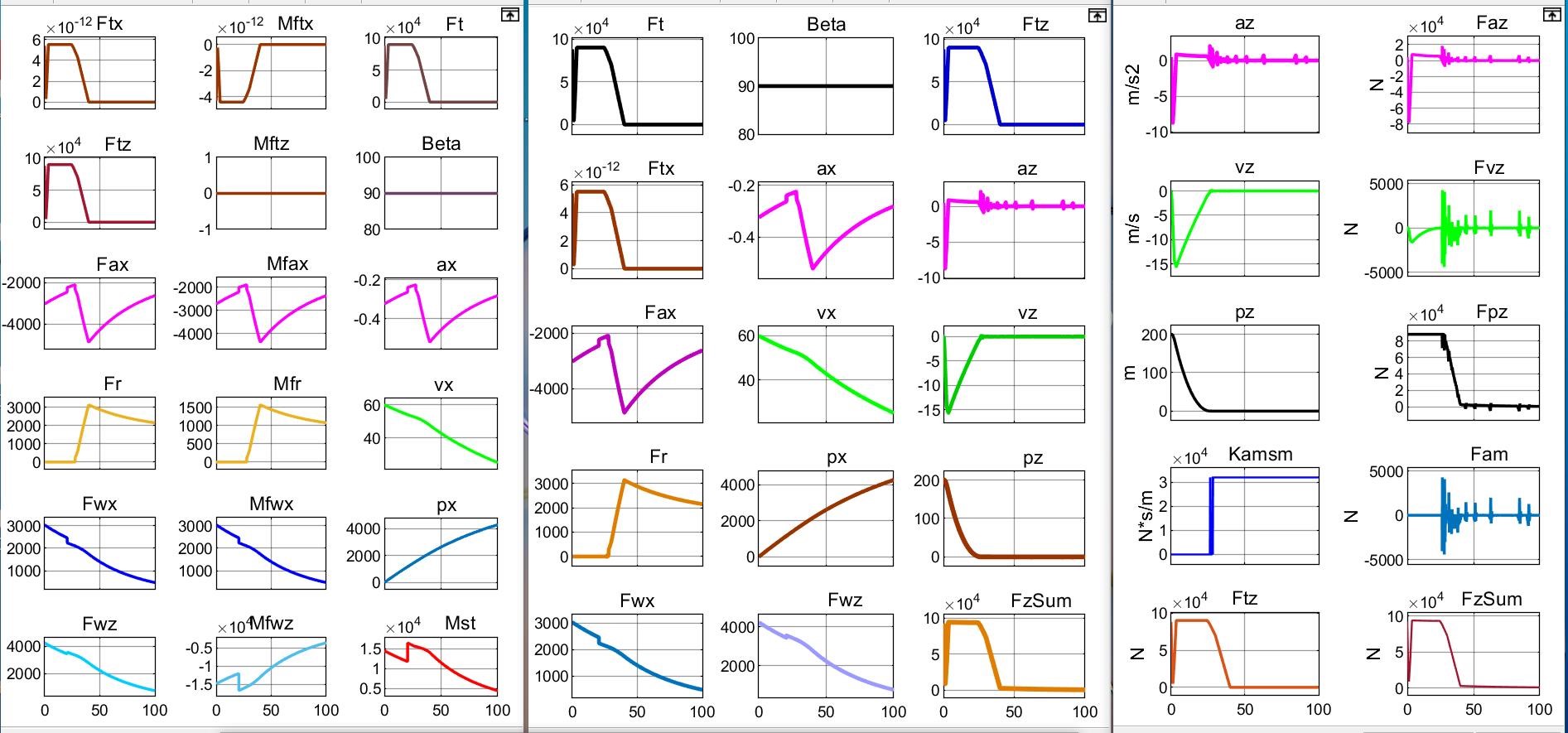
Рисунок 12 - Совокупность показателей процесса спуска ПОТ Davis c высоты pz0=200 м при начальной скорости Vx0 = 60 м/с
Примечание: FT = 90 кН, β = 90°
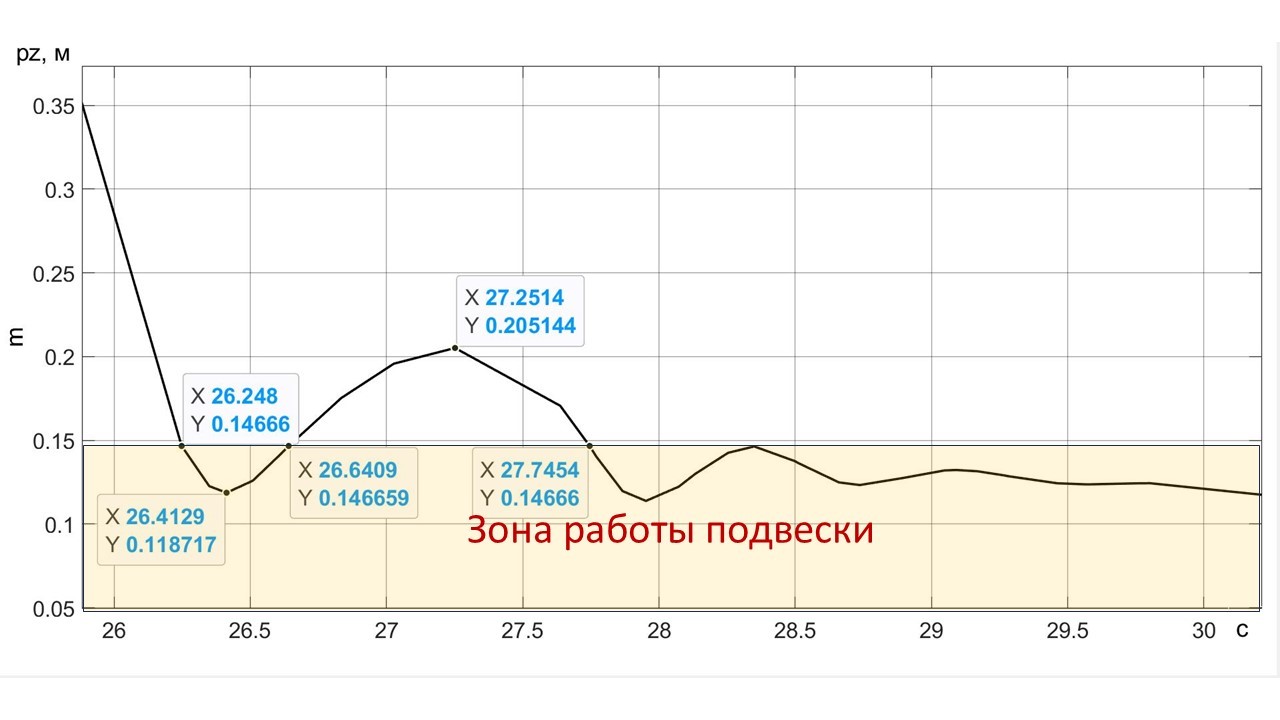
Рисунок 13 - Вертикальное перемещение ПОТ Davis в зоне касания колесами ОП при начальной скорости Vx0 = 60 м/с
Примечание: FT = 90 кН, β = 90° в фазе IV ПСП
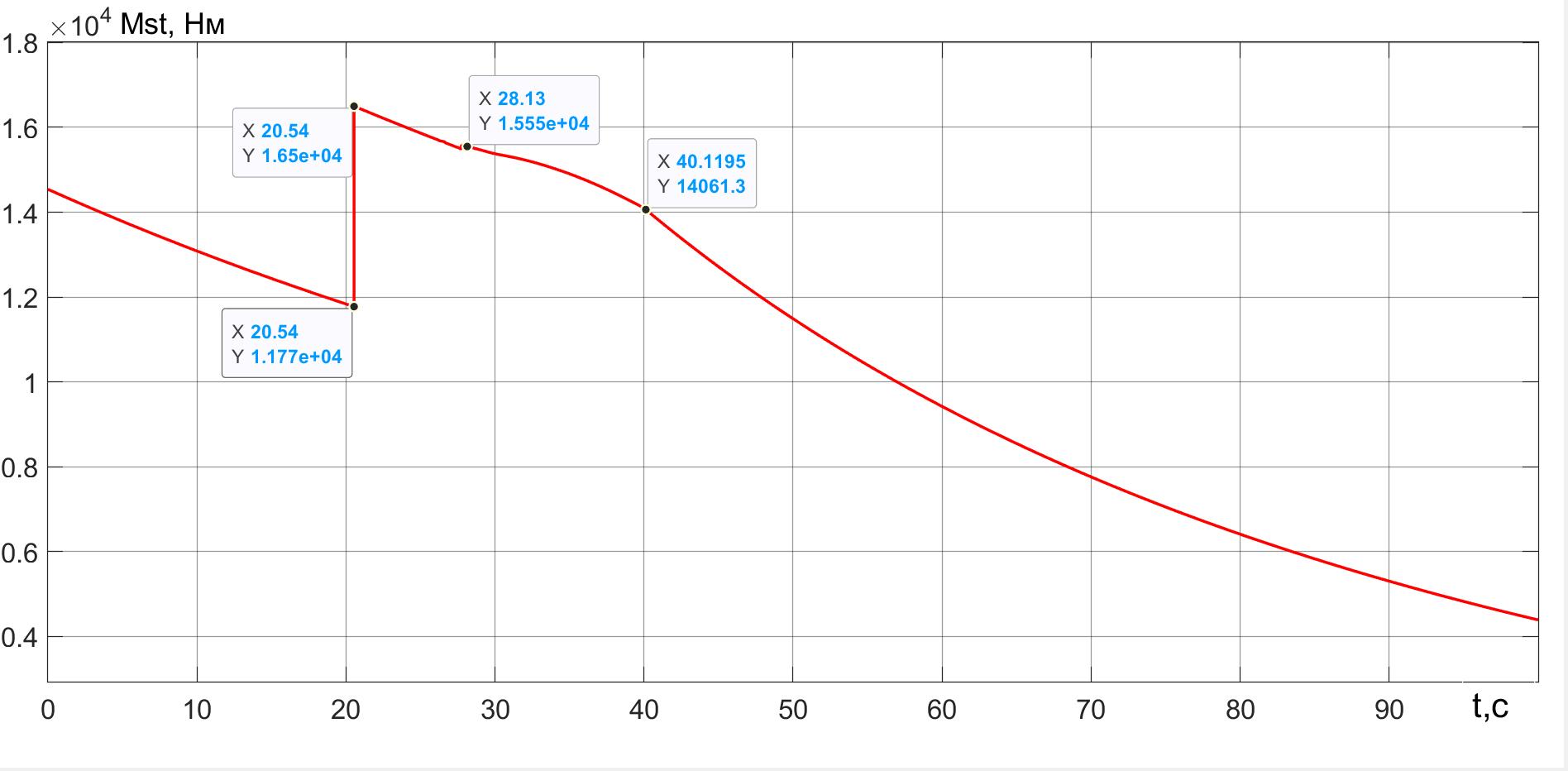
Рисунок 14 - Требуемый стабилизирующий силовой момент Mst в процессе спуска и приземления ПОТ Davis при начальной скорости Vx0 = 60 м/с
Примечание: FT = 90 кН, β = 90°
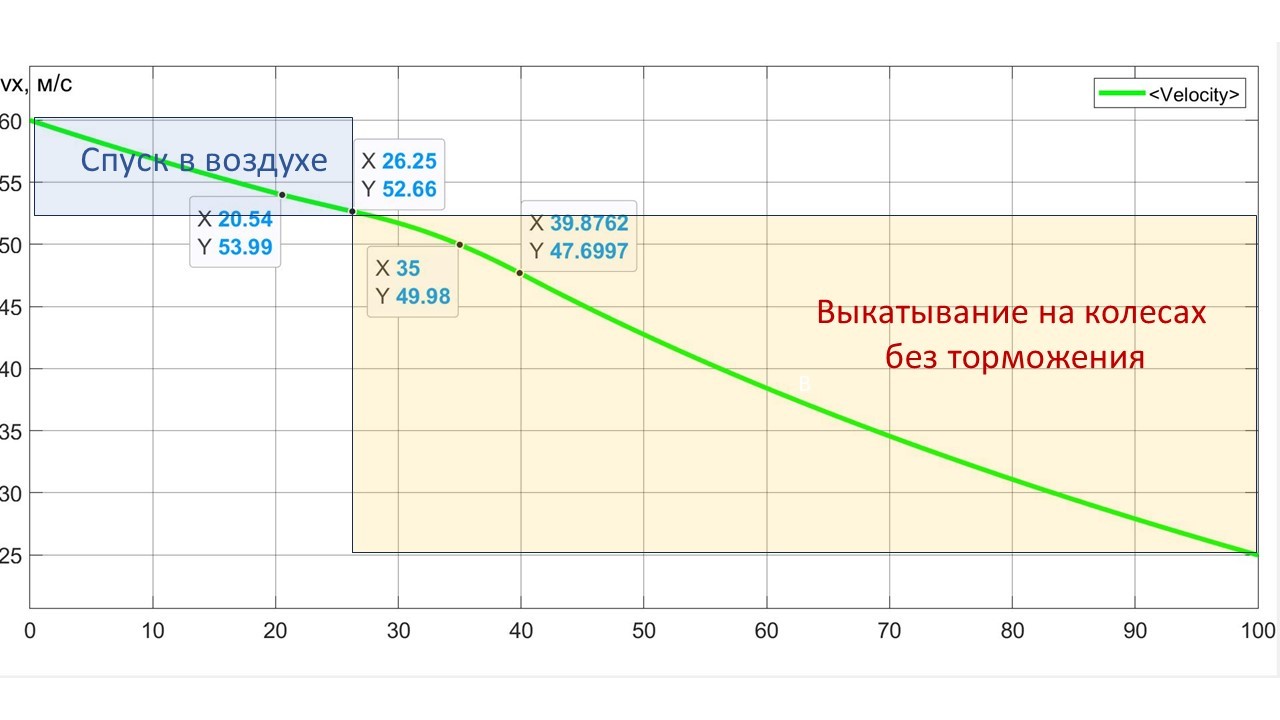
Рисунок 15 - Изменение продольной скорости ПОТ Davis во времени в процессе спуска и приземления при начальной скорости Vx0 = 60 м/с
Примечание: FT = 90 кН, β = 90°
4. Обсуждение результатов расчетов
Совокупность выполненных расчетов нацелена, во-первых, на демонстрацию возможностей МПДК в части представления особенностей спуска и приземления квантомобилей, а во-вторых, — на построение каркаса опорных граничных вариантов для перспективной оптимизации стратегий посадки в этой структуре.
4.1. Представление особенностей спуска и приземления квантомобиля
Обсуждение начнем с простейшего – спуска и приземления экипажа из вывешенного положения с Vx0 = 0, см. рис. 5. Задающий вектор FT (t) приведен на рис. 7, на котором отмечены 4 фазы ПСП. Для поддержки неподвижного висения необходимо при β = 90° прикладывать силу FT = Gq = 88 кН. Потерянный импульс силы ∫03(Gq–FТ)dt за 3 сек фазы I (коричневый ареал на рис. 7) частично восполняется импульсом ∫342(FТ – Gq)dt в фазах II и III (синий ареал). Чем больше FT (а в более общем случае — FzSum), тем меньше требуется времени до восстановления потерянного импульса.
На временнóм графике спуска рис. 8 отмечены характерные точки: время t = 28,86 c спуска до высоты Hlf3 ≈ 25 м; время t = 36,05 c спуска до высоты Hlf2 = 10 м; t = 45,02 c спуска до касания колесами ОП на высоте Hlf1 = 0,1467 м; t = 45,19 c спуска до низшей точки глиссады Нlfg= 0.0017 м, предваряющей колебательный процесс экипажа на подвеске; t = 46,3 с высоты первого отскока экипажа Hlfk = 0,4698 м.
Часть из этих точек можно найти на детализированном графике рис. 9. Отметим наличие небольшого «козления» экипажа во временнóм интервале (45,43 ÷ 47,08) с.
Вход в зону работы подвески характеризуется ускорением упруго-вязкостного удара (связанного с подключением элементов подвески). Возникновение этого ускорения экипажа в точке (t = 45,02; pz = 0,1467) можно проследить на рис. 10. При отскоке и выходе из зоны работы подвески вертикальное ускорение экипажа, связанное с упругим сопротивлением подвески, в момент времени t = 45,43 с переходит в ускорение, связанное только с сопротивлением воздуха.
Рассмотренный вариант спуска и приземления можно отнести к способу посадки VTOL.
Наличие продольной скорости экипажа Vx0 ≠ 0 в начальный момент спуска меняет 2D-картину перемещения, что можно видеть на рис. 11 (сравните с рис. 5). Насыщение продольной динамики можно отметить, сравнивая совокупности показателей на рис. 6 и рис. 12.
Сравнивая кратковременные фрагменты рис. 9 и рис. 13, можно отметить, что, во-первых, характер колебательного процесса сохранился (и три периода до затухания свидетельствуют о добротности подвески). А во-вторых, время спуска по условию |az(t)| < 10 м2 существенно снизилось.
Наличие продольной скорости приводит к значительному увеличению опрокидывающего момента (см. , ). Требуемый стабилизирующий момент Mst в процессе спуска квантомобиля динамически меняется, что видно на рис. 14. Во-первых, он со снижением продольной скорости в целом уменьшается. Во-вторых, он существенно реагирует на изменение конфигурации экипажа — см. ступенчатый рост Mst при t = 20,54 c (когда на высоте pz = 10 м выдвигается шасси и задвигается оперение — условно это происходит мгновенно).
Приземление к 30-й секунде (по окончании колебаний — рис. 13) завершается и далее может следовать одна из трех активностей: принудительное торможение, выкатывание, либо запланированное движение по наземному маршруту. На рис. 15 представлено выкатывание. За 30 с спуска и приземления экипаж продвинулся на расстояние 1500 м — см. рис. 11, а).
Рассмотренный вариант спуска и приземления может быть отнесен к способу посадки CTOL, либо STOL– в зависимости от использования траста и процедуры торможения.
4.2. Формирование каркаса опорных вариантов спуска
Для построения каркаса опорных вариантов максимально интенсивного спуска ПОТ Davis результаты ПИМ сведены в таблицу 2. В ней отражены значения времени спуска tpzОП с высоты pz0 = 200 м до высоты Hlf1 = 0,147, на которой колеса экипажа начинают касаться ОП. Входными параметрами таблицы являются скорость продольного движения экипажа в начале спуска Vx0 и угол наклона траста β в процессе спуска.
Таблица 2 - Минимально возможное время спуска ПОТ Davis tpzОП (с) с высоты 200 м из условия непревышения ускорения |az(t)| = 10 м/с2
β, град | Vx0, м/с | |||
0 | 20 | 40 | 60 | |
90 | 45,0 | 39,6 | 31,5 | 26,2 |
85 | 43,1 | 36,4 | 28,8 | 24,7 |
80 | 40,5 | 31,8 | 26,6 | 21,8 |
Значения вычислены в процессе ПИМ из условия непревышения ускорения (в том числе ударного) |az(t)| = 10 м/с2 — с целью построения поверхности, ограничивающей пространство траекторий спуска, допустимых по этому условию. Бóльшие значения времени спуска создают условия для более плавного спуска с |az(t)| < 10 м/с2, меньшие — недопустимы.
Граничная поверхность, сформированная в Matlab по данным табл. 2, представлена на рис. 16.
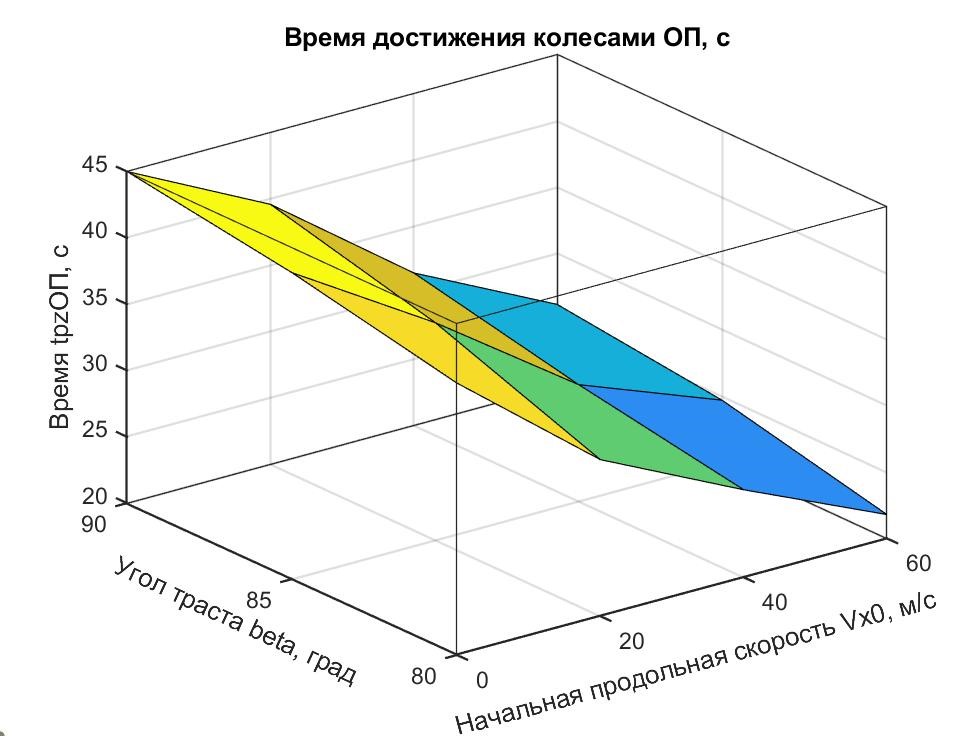
Рисунок 16 - Поверхность tpzОП = f (Beta, Vx0), ограничивающая семейство траекторий спуска ПОТ Davis по условию |az(t)| < 10 м/с2
Сценарии охватывали 3 фазы:
1) ступенчатый сброс значения Ft со значения 88 кН (поддержка висящего экипажа) до минимума в диапазоне 0 ÷ 50 кН с последующим быстрым ростом до максимума Ft = 90 кН (см. рис 7 первые 3 сек);
2) выдержка максимального Ft = 90 кН до значений pz ≈10 м (см. рис. 8);
3) манипуляция с ниспадающим Ft (с целью выполаживания глиссады) с выходом в зону вступления в действие подвески (см. рис. 8 и 9).
Визуальный анализ поверхности рис. 16 позволяет отметить следующее.
Уменьшение времени спуска tpzОП при снижении угла наклона вектора траста β с 90° до 80° объясняется уменьшением ТПС FTz при уменьшении β, приводя к ускорению спуска. Снижение времени спуска tpzОП при увеличении начальной продольной скорости Vx0 можно пояснить с помощью рис. 17. Прирост количества движения за счет АПС Fwz (импульса силы ∫Fwzdt) характеризуется площадью трапеции ABCD. Чем больше начальная, стало быть, и последующие скорости, тем меньше требуется времени в фазе II спуска для восполнения импульса силы, утраченного в фазе I (см. рис. 7).
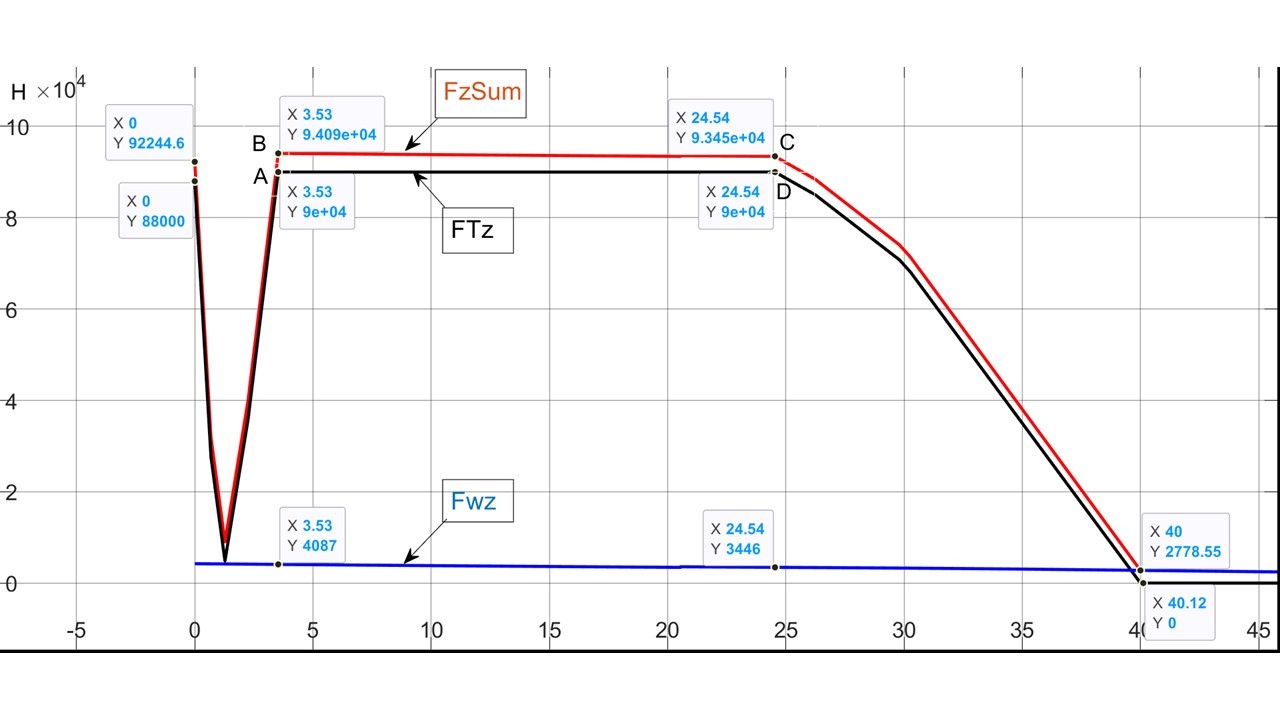
Рисунок 17 - Интерпретация роста количества движения за счет использования АПС Fwz
Таблица 3 - Минимально возможное время спуска ПОТ 1-Box tpzОП (с) с высоты 200 м из условия непревышения ускорения |az(t)| = 10 м/с2
β, град | Vx0, м/с | |||
0 | 20 | 40 | 60 | |
90 | 51,3 | 49,8 | 50,4 | 51,1 |
80 | 41,0 | 41,2 | 41,0 | 41,3 |
Результаты, помещенные в табл. 3, аппроксимированы поверхностью, представленной на рис. 18. Видим, что влияния начальной скорости Vx0 на величину tpzОП нет — это потому, что отсутствует АПС (cl = 0). Влияние угла наклона траста β для 1-Box подобно случаю с ПОТ Davis.
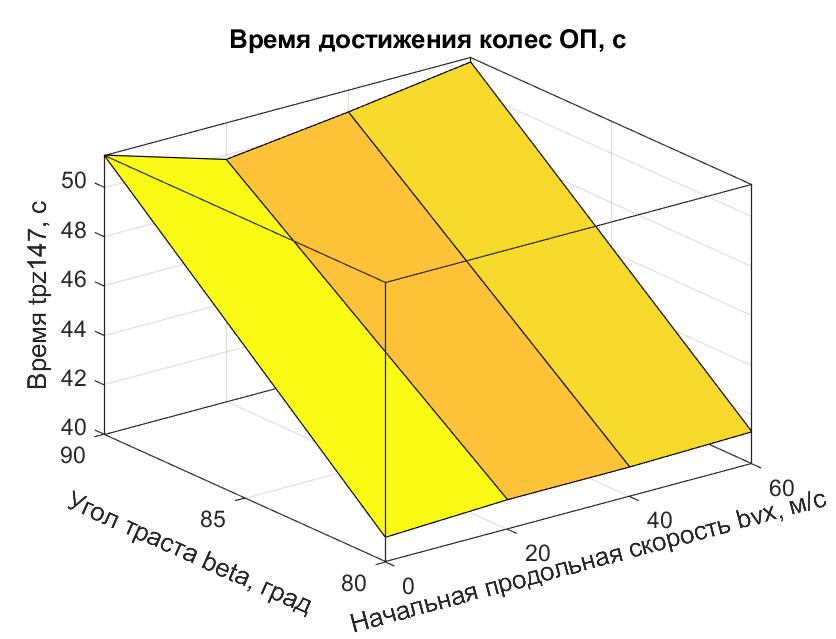
Рисунок 18 - Поверхность tpzОП = f (β, Vx0), ограничивающая семейство траекторий спуска ПОТ 1-Box по условию |az(t)| < 10 м/с2
Можно утверждать, что для любого ТС с КДД можно построить поверхность максимально интенсивного спуска (в пределах допустимых ускорений) с назначенной высоты, с учетом начальной продольной скорости спуска Vx0, величины вектора траста Ft(t) и его угла наклона β(t) в процессе спуска. По одну сторону от поверхности будет полупространство допустимых по мягкости посадки вариантов, по другую — полупространство недопустимых вариантов. Такая граничная поверхность будет способствовать сепарации режимов спуска при моделировании движения по маршруту с препятствиями, также — в технологии беспилотного управления экипажем.
Возможность непрерывного перехода в управлении спуском и приземлением экипажем с КДД от вертикального траста КД к наклонному с вариабельностью значений FT определяет охват всех трех условных способов: CTOL, STOL и VTOL – с непрерывным же переходом между ними.
5. Заключение
В среде авторской Модели приземного движения квантомобиля (МПДК) сформирована четырехфазовая Процедура спуска и приземления (ПСП) с прослеживанием движения по реперным высотным точкам: начальная высота; высота безопасности; высота трансформации подвески и оперения; высота касания колесами ОП; высота завершения приземления.
С привлечением ПСП построена методика управления задающим вектором траста КД в процессе максимально интенсивного спуска-приземления ТС с наложенным ограничением на максимум вертикального ускорения. В этом случае четырехфазовый алгоритм (падение, нейтрализация падения, выполаживание глиссады, работа подвески) допускает кратковременное свободное падение экипажа с подхватом его после этого управляемой трастовой подъемной силой (ТПС), с обеспечением допустимых ускорений удара при переходе колес из воздуха на ОП.
На базе двух примеров сформирована методика построения поверхности, ограничивающей минимум времени спуска по условию непревышения предписанного вертикального ускорения ТС. Методика нацелена на обеспечение (водителя и/или автомата) прогностической оценкой допустимого времени спуска.
Важным научным результатом исследования можно считать подкрепление гипотезы: с внедрением в ТС квантового двигателя моделирование посадки экипажа станет возможным по единому алгоритму, охватывающему варианты посадки — CTOL, STOL и VTOL. Эта констатация комплементарна аналогичному ранее вынесенному утверждению по этапу взлета квантомобиля , что приводит к возможности их объединения и реализации единого алгоритма взлета-посадки — как в цикле движения ТС с КДД, так и в его произвольном высотном маневрировании.
Объединяющим фактором синтеза трёх названых способов взлета и посадки, является наличие управляемой ТПС КДД. Собственно говоря, технологический и конструктивный смысл разнесения функции подъема и спуска ТС с КДД на три категории (CTOL, STOL и VTOL) в этом случае исчезает.
Приведенные результаты исследования обладают новизной и оригинальностью.
Дальнейшие исследования должны быть направлены на рассмотрение возможности применения развиваемого подхода к оптимизации траекторий движения квантомобилей, возможно, главным образом, беспилотных. Также развитие представленного метода будет полезным для моделирования движения квантомобилей при преодолении водных и иных преград, посадки и высадки на борт судов, доставки породы в карьерах и другое.
