FORMATION OF REQUIREMENTS TO THE ENERGY PRICE OF QUANTOMOBILE PROPULSION SYSTEM THRUST
FORMATION OF REQUIREMENTS TO THE ENERGY PRICE OF QUANTOMOBILE PROPULSION SYSTEM THRUST
Abstract
The prospect of introduction of quantum cars using the thrust of a quantum engine (QE), implemented in the pitch plane, requires consideration of the energy of the crew motion. This will contribute to the requirements for the energy efficiency of the QE and its energy acceptability. In the absence of full-scale facilities, the study is based on simulation modelling, flexible model and powerful software. Expressing the transport work as the product of force by collinear displacement is unable to account for the work of vertical lift force in calculating the longitudinal propulsion performance of the disembodied quantum vehicle. The vertical component of the trust (lift) helps to reduce the drag on the propulsion of the support wheels and the associated energy inputs. However, providing lift requires its own energy costs, the calculation of which is problematic for existing models of longitudinal ground vehicle (GV) motion. A methodology for estimating acceptable energy costs for a lift is developed. The methodology uses the author's model of ground motion of a quantum vehicle (MGMQA). It allows estimating the level of the required energy price of thrust (EPT) of the QE, below which the superiority of the quantomobile in terms of energy efficiency over the analogue vehicle is ensured. In a series of calculations of acceleration and steady-state motion of the vehicle for various resistances of supporting surfaces and angles of inclination of the trust vector it is found out that in order to ensure superiority over the car-analogue KamAZ-4326 the EPT of the lift at the concept cargo quantomobile should be not more than 55 W/N. On the basis of comprehension of the calculation results, the cognitive difficulty of obtaining the estimation of realized work (energy consumption) for the movement of the suspended ground vehicle is overcome. MGMQA is considered as a basis for the development of modelling of quantum car motion in arbitrary conditions.
1. Введение
В современной физике развиваются идеи извлечения энергии из физического вакуума (ФВ) , , . На базе этих идей рассматриваются концепции квантовых двигателей (КД) , . И хотя получаемые импульсы траста (тяги) КД пока малы, надежда на практическую реализацию названых идей становится все более существенной , .
Реализация идеи КД приведет к появлению нового типа транспортных средств (ТС) – квантомобилей , , . Cтанет возможным прикладывать траст КД к корпусу экипажа непосредственно (без трансмиссии). Необходимость трансмиссии отпадет, колесам останется только опорная функция. При наклоне вектора траста в плоскости тангажа появляется вертикальная компонента, которую можно будет использовать для вывешивания (лифта) квантомобиля. Горизонтальная компонента траста при этом используется для преодоления сил сопротивления продольному движению экипажа , , .
В публикациях , рассмотрена методика и даны примеры расчета тяговых сил квантомобилей для наземной среды движения ТС с возможным полным переходом в воздушную среду. Показывается, что расчетная методика, в связи с необходимостью учета лифта, отличается от традиционных алгоритмов расчета силового баланса автомобиля.
В работах , затронута возможность создания всесредного мультимодального квантомобиля, способного функционировать во всех физических средах. Обобщением этих аспектов является авторская инициатива формирования теории квантомобиля , .
Вертикальная компонента траста (лифт) способствует снижению сопротивления движению опорных колес и соответствующих энергозатрат. Однако на обеспечение лифта требуются свои затраты энергии, расчет которых для существующих моделей продольного движения наземных ТС проблематичен. Необходим алгоритм сравнения энергозатрат по этим конкурирующим факторам в пределах общей транспортной работы ТС , .
Выражение транспортной работы в виде произведения силы на коллинеарное перемещение, не способно учитывать работу силы вертикального лифта при расчете показателей продольного (горизонтального) продвижения вывешенного квантомобиля. Но работа на вывешивание экипажа ведь совершается! Этот кажущийся парадокс требует разрешения.
Возникающая концепция квантомобиля с её проблемами требует совместного рассмотрения динамики и энергетики движения экипажа с КД. Сформированная автором в среде ППП Matlab-Simulink Модель приземного движения квантомобиля (МПДК) , , направлена, в том числе, на расчетное исследование сочетания динамических возможностей и сопутствующих энергозатрат квантомобиля. На базе этих исследований предполагается формирование требований к энергоэффективности этого перспективного ТС.
Основным условием необходимости и успешности внедрения новых технических средств в практику, как известно, является их должное превосходство перед прототипическими средствами предыдущих поколений по показателям их эксплуатационных свойств, в том числе по энергоэффективности. Одним из показателей энергоэффективности ТС является энергетическая цена тяги (ЭЦТ) – отношение реализуемой мощности к силе тяги (power-to-thrustratio) , , , . Попробуем оценить границу зоны превосходства перспективных квантомобилей перед существующими автомобилями-аналогами посредством оценок ЭЦТ. Очевидно, это потребует специфической проработки исследования свойств рассматриваемого гипотетического объекта.
2. Методы и принципы исследования
2.1 Цель и задачи исследования
Целью расчетного исследования явилась методическая проработка формирования требований к энергоэффективности силовой установки квантомобиля, обеспечивающих улучшение энергетических показателей движения относительно существующего автомобиля-аналога.
Отсутствие признанных теоретических основ движения квантомобиля (обладающего новыми свойствами относительно традиционного автомобиля), натурных образцов исследуемых объектов и эмпирических данных по ним, вызывает необходимость использовать подход с опорой на программное имитационное моделирование (ПИМ).
Задачами по достижению цели являются:
1) формирование математической модели продольного движения квантомобиля (МПДК) под поставленную цель;
2) построение Simulink-модели движения квантомобиля с детализацией составляющих энергозатрат на преодоление сопротивлений движению и вывешивание экипажа, с формированием модели конкурентоспособности на базе ЭЦТ; с отработкой интерфейса взаимодействия с моделью и многофакторного вывода результатов;
3) на базе Simulink-модели проведение ПИМ с экспериментами, охватывающими обоснованное множество вариантов разгона и установившегося движения ТС;
4) обсуждение и обобщение результатов расчетов;
5) формирование рекомендаций и выводов.
2.2 Постановка проблемных вопросов
В настоящем исследовании начало цепочки энергопреобразований начинается с подачи на корпус квантомобиля траста FT под углом β к горизонту , , , . Вопросы физической генерации траста, энергопреобразования в недрах конструкции КД и эффективности процесса извлечения энергии из ФВ здесь не затрагиваются. То есть, ограничиваясь компетенциями транспортников, полагаем, что физики и инженеры-энергетики предоставят функционирующий КД, обеспечивающий экипаж трастом FT. Решаем вопросы представления и расчета механической работы, совершаемой экипажем при продольном движении под воздействием этого траста. Отмечаем при этом, что классический подход для моделирования движения ТС, развитый в теории автомобиля, в нашем случае недостаточен, поскольку в механику движения квантомобиля, при реализации наклонов вектора траста в плоскости тангажа, внедряется вывешивание (лифт) экипажа.
С проблемами вывешивания экипажа сталкиваются в ракето- , самолето- , вертолетостроении , . В этих областях по-разному рассчитывают вклад горизонтальных и вертикальных сил в формирование общих энергозатрат на горизонтальное перемещение ТС. Общим положением, однако, можно отметить использование в расчетных методиках понятия ЭЦТ (power-to-thrust ratio , , , (Вт/Н, кВт/Н, Вт/мН)).
Общим является также аддитивный характер суммы скалярных величин мощности и энергии, связанных с реализацией соответствующих сил (векторов) различной направленности.
Будем использовать в исследовании величины и их обозначения:
– ЭЦТ KNF = N/F, где N – реализуемая мощность, F – скаляр силы;
– Коэффициент энергоэффективности (КЭ) KFN = F/N.
Введем также понятия и обозначения:
– Энергетическая цена вертикальной тяги (ЭЦВТ) KNF_h;
– Энергетическая цена горизонтальной тяги (ЭЦГТ) KNF_l.
Важно отметить, что величины KNF, KNF_h и KNF_l имеет размерность скорости (в системе СИ – м/с), поскольку N = F · V, откуда следует [N/F] = [V] = м/с. Это коррелирует с ролью скорости в определении мощности (как «скалярной физической величины, характеризующей мгновенную скорость передачи энергии от одной физической системы к другой в процессе использования энергии» ).
В вышеназванных областях транспорта оценки ЭЦТ формализуются аналитически, но на базе необходимого экспериментального материала. В табл. 1 приведены некоторые оценки этих показателей, полученные по результатам авторского обзора.
Таблица 1 - Показатели удельной тяги двигателей (силовых установок)
№ | Двигатель | Цена тяги ЭЦТ KNF, кВт/Н | Коэффициент энерго- эффективности КЭ KFN, Н/кВт | Источник |
1 | Йонный двигатель ИД-500 | 46,7 | 0,0214 | |
2 | Стационарный плазменный двигатель СПД-230 | 26,6 | 0,0376 | |
3 | Стационарный плазменный двигатель СПД-140Д | 15,5 | 0,0645 | |
4 | Ракетный ЖРД | 1,43 | 0,7 | |
5 | Винтокрылый носитель для воздушного старта ракет | 0,03 | 33 | |
6 | Мультироторный геликоптер | 0,016 | 62 | |
7 | Однороторный геликоптер | 0,01 | 100 | |
8 | Беспилотник | 0,009 | 112 | |
9 | Лабораторная КД-установка Леонова В.С. (в импульсном режиме) | 0,009 | 115 |
Встают вопросы:
– Каков уровень ЭЦВТ KNF_h приемлем для лифта квантомобиля?
– Каков уровень ЭЦГТ KNF_l характерен для продольного движения квантомобиля?
– Где в диапазоне представленных табл. 1 значений найдут место показатели ЭЦТ для квантомобиля?
– Как энергообеспеченность вертикальной компоненты траста будет влиять на динамику продольного движения квантомобиля?
– Каковы те граничные значения KNF, ниже которых квантомобиль будет обладать энергоэффективностью лучшей, нежели прототипируемый автомобиль того же класса?
В отсутствие натурных образцов квантомобиля попытаемся найти ответ на эти вопросы с помощью имитационных экспериментов (ПИМ).
2.3 Суммирование ортогональных компонент вектора траста и связанных с ними скаляров мощности и энергии
В рамках продольного движения экипажа в плоскости развёртывания угла тангажа β (см. рис. 1) – вектор траста FT раскладывается на две ортогональные компоненты FTx и FTz , , :
FT = FTx + FTz. (1)
В скалярной записи это:
FT = sqrt(FTx2 + FTz2). (2)
Угол наклона вектора FT
β = arctg(FTz / FTx) = arctg(FTz / sqrt(FT2 – FTz2)). (3)
FTx= FT· cosβ, FTz = FT· sinβ. (4)
Графически это представимо рис. 1.
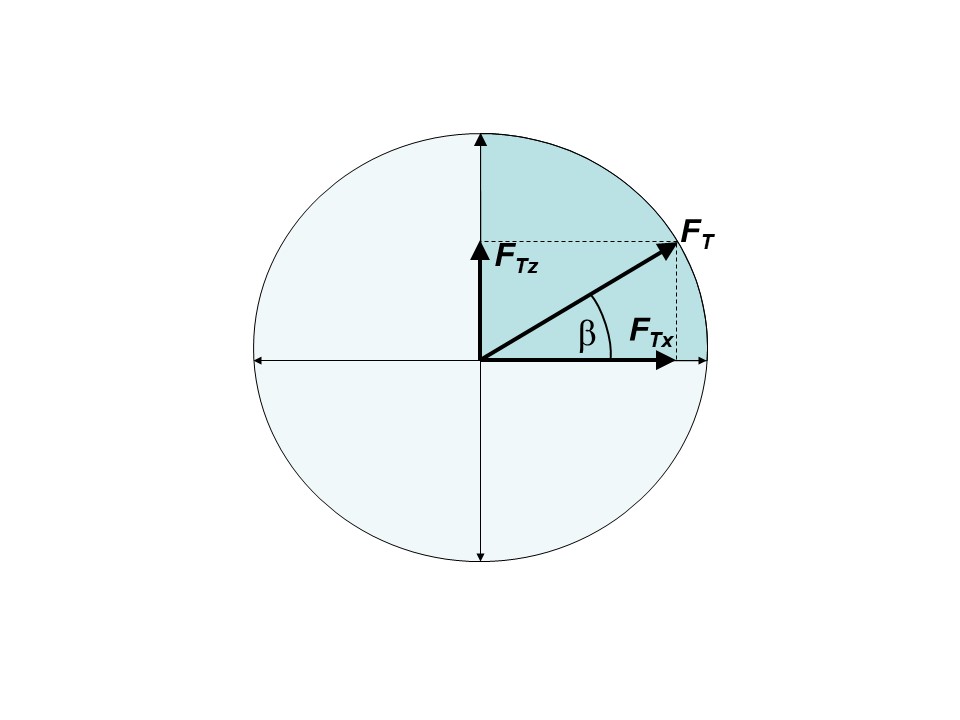
Рисунок 1 - Разложение вектора траста FT на горизонтальную FTx и вертикальную FTz компоненты:
β – угол наклона вектора FT относительно горизонта
Освободимся от вопросов формирования, моделирования и реализации аэродинамической подъемной силы, сосредоточившись на рассмотрении лифта, обеспечиваемого только вертикальной компонентой FTz траста FT (как бы осуществляя схему «плохообтекаемого движущегося короба» ).
Также, приняв вертикальные перемещения ТС при наземном движении незначительными, в сравнении с исследуемыми длительными горизонтальными перемещениями его, освободимся от необходимости учета динамики вертикальных перемещений ТС (вообще-то существующей из-за упругости подвески).
Допуская, что между КД и корпусом экипажа могут устанавливаться промежуточные устройства, все же используем в анализе непосредственное приложение силы FT к корпусу экипажа.
Акцентируем внимание на том, что в отличие от геометрической векторной суммы силовых компонент FTx и FTz (см. выражение (1) и его скалярный вариант (2)), соответствующие мощности NFTx и NFTz, а также величины работы AFTx и AFTz, являясь скалярными величинами, складываются алгебраически – скалярно, аддитивно , то есть:
NFT = NFTx + NFTz, (5)
AFT = AFTx + AFTz. (6)
2.4 Идейная основа оценки энергетики продольного движения квантомобиля с учетом вывешивания
Вышеприведенные допущения позволяют использовать вариант уравнения силового баланса квантомобиля, обоснованного автором в публикациях , , , а именно:
где FTx – продольная сила тяги КД, Н;
Fr – сила сопротивления качению ведомых опорных колес, Н;
Fw – сила сопротивления воздуха продольному движению, Н;
Fa – сила инерции, противодействующая ускорению экипажа, Н;
Gq' – сила давления экипажа на ОП с учетом лифта, Н;
fk0 – коэффициент сопротивления качению колес при нулевой скорости;
fkv – скоростной коэффициент сопротивления качению колес, с2/м2;
cd – коэффициент аэродинамического сопротивления, безразмерный;
ρw – плотность воздуха, Н ×с2/м4;
Sfi – лобовая площадь экипажа, м2;
Gq – исходный вес квантомобиля, Н;
g – ускорение свободного падения, м/с2;
a – продольное ускорение экипажа, м/с2;
δwh – коэффициент инерции вращения опорных колес экипажа.
Сила Gq' = Gq – FTz. Для квантомобиля приведенная масса m’ = Gq(1+δwh)/g учитывает вращение только опорных колес, поскольку вращающиеся детали традиционного силового привода отсутствуют.
График прикладываемых к экипажу сил имеется в , , .
Расчет мощностей NFr, NFw и NFa реализации продольных сил Fr, Fw и Fa в процессе имитации движения на базе уравнения (7) осуществляем по формуле N(t) = F(t)·V(t). Расчет значений работы AFr, AFw и AFa, накапливаемой во времени действием сил Fr, Fw и Fa, производим по формуле A(t)=F(t)·S(t); используем также программный интегратор.
Работа вертикальной силы лифта FTz при горизонтальном движении экипажа не может быть рассчитана по канонам классической механики. Подход Иванова Е.М. перехода от пути S ко времени t, с использованием импульса силы, – в нашем случае неприменим (поскольку относится только к свободному телу – без учета сопротивлений воздуха Fw и ОП Fr). Поэтому реализуем нижеследующие идею и соответствующий алгоритм.
Идея определения допустимого (с точки зрения непревышения суммарной работы невывешенного экипажа) граничного значения ЭЦВТ заключается в сравнении энергетики продольного движения экипажа при том же самом FT до одинаковой конечной скорости разгона (и/или установившегося движения) в двух крайних вариантах управления углом наклона вектора траста:
1) при β = 0° (когда вывешивание отсутствует (FTz = 0), Fr > 0, а FTx=FT), с фиксацией FTx = FT, NFTx и AFTx на максимально возможной скорости движения Vmax;
2) при β = arctg(Gq/sqrt(FT2–Gq2) = βmax (когда экипаж полностью вывешен (FTz = Gq), Fr = 0, а FTx < FT), но при Fr = 0 остается горизонтальная составляющая траста FTx, необходимая и достаточная для осуществления разгона и установившегося движения ТС на зафиксированной по пункту 1) скорости Vmax; здесь также фиксируются FTx, NFTx и AFTx на скорости Vmax;
3) определение ЭЦВТ KNF_h = NFTzdif / FTz, где NFTzdif = NFT – NFTx, и NFTx относится к варианту β = βmax.
Тогда равенство конечных скоростей разгона Vmax обеспечит равенство накопленной кинетической энергии mV2/2 (работу силы Fa), а также приблизительное равенство двух вариантов работы силы воздушного сопротивления Fw (разница может накопиться при разной реализации темпа разгона во времени; при установившемся движении разницы не будет). При переходе от β = 0° к βmax работа силы сопротивления качению колес AFr (в составе полной работы AFT) заменится работой силы лифта AFTz. Таким образом, величина AFr при β = 0° может служить оценкой работы силы лифта AFTz при β = βmax в составе полной работы по осуществлению движения.
По-другому, разница между величиной полной работы AFTx =AFT при β = 0° и AFTx<AFT при β = βmax представляет собой работу силы лифта AFTz.
Обозначим максимальную скорость экипажа при реализации FT с углом наклона вектора траста β через Vmaxβ.
Теперь для разности мощностей NFT и NFTx (т.е. мощности NFTzdif, высвобождаемой для лифта при уменьшении горизонтальной тяги путём вывода вектора траста на угол β) с учетом (4) можно записать:
NFTzdif = NFT – NFTx = FT·Vmaxβ – FT·Vmaxβ·cosβ = FT·Vmaxβ (1–cosβ). (8)
Тогда KNF_h = NFTzdif / FTz = Vmaxβ (1–cosβ) / sinβ. (9)
2.5 Программное обеспечение модели МПДК
Структура имитационной системы представлена на рис. 2. Она состоит из трех подсистем: Scenario – для выработки задающего вектора FT и угла β; Vehicle Dynamics – расчета показателей динамики продольного движения экипажа (см. , , ); Energetics – расчета показателей энергетики движения (рис. 3).
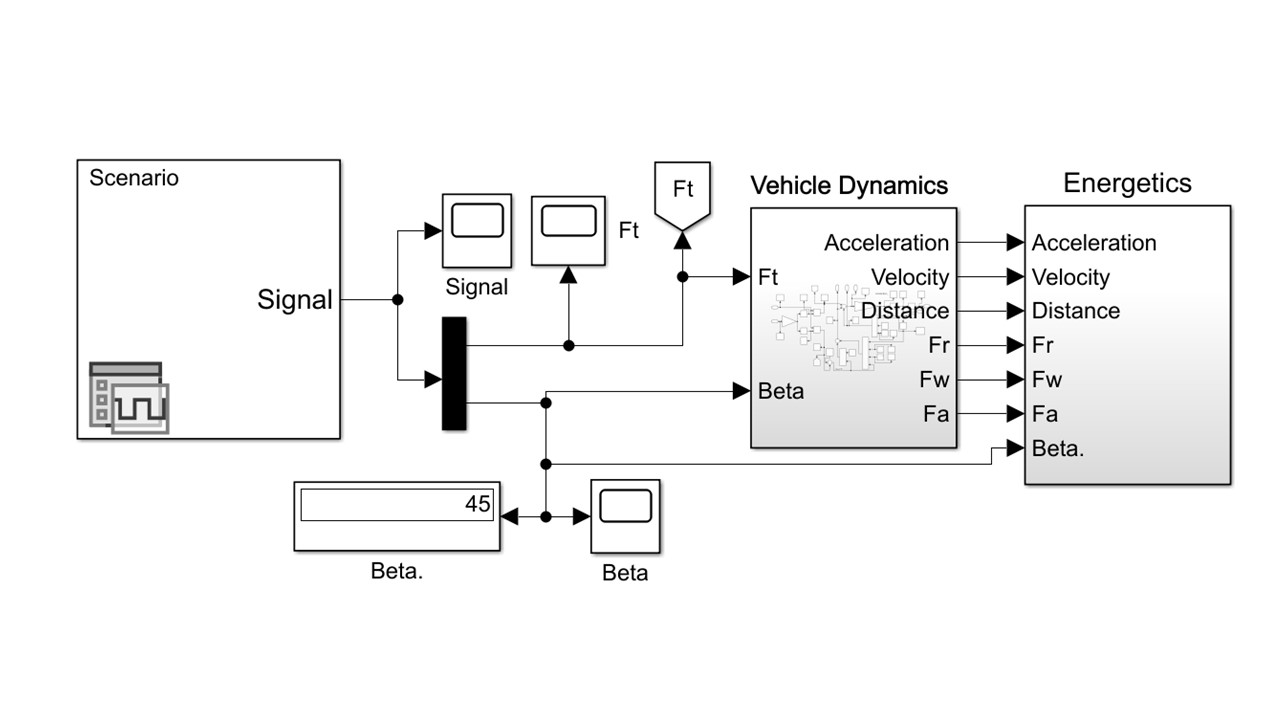
Рисунок 2 - Главный модуль S-модели МПДК
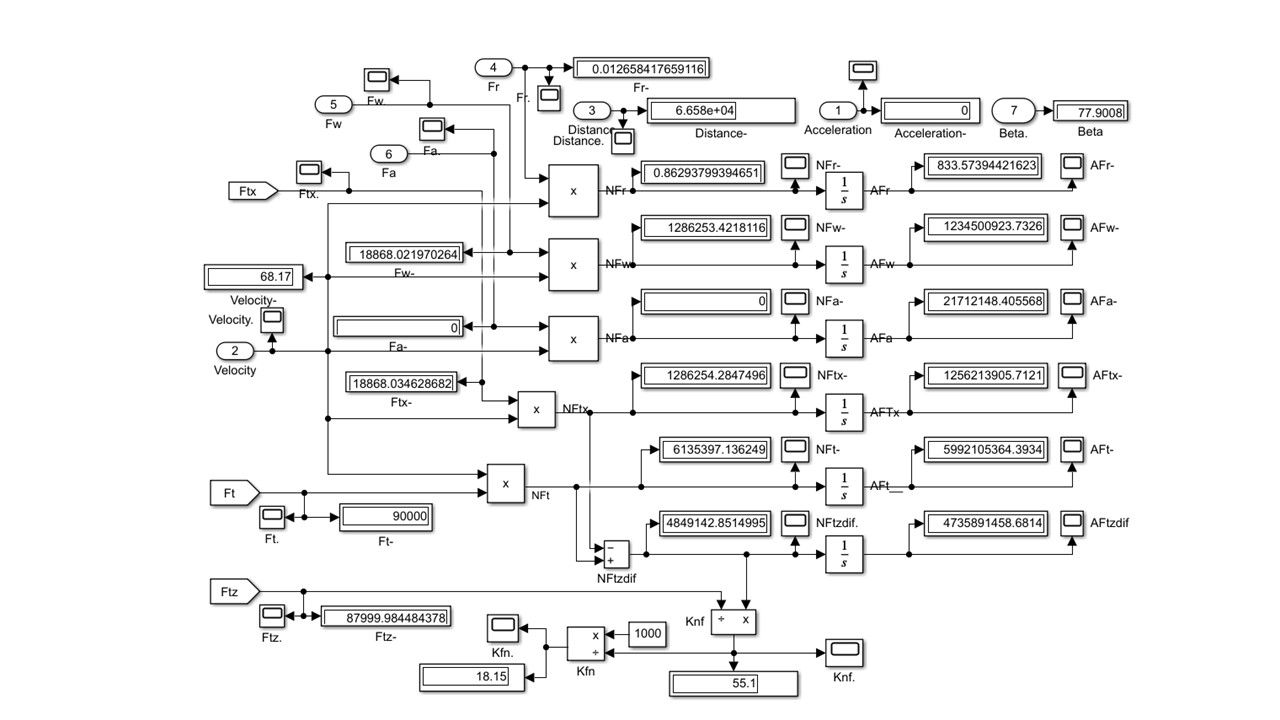
Рисунок 3 - Подсистема Energetics
Примечание: зафиксированы результаты разгона вывешенного экипажа по ОП с fk0=0,3 при угле наклона траста β = 77,9°; tr =1000c
Путем кликования Осциллографов графики процессов изменения соответствующих величин могут быть вынесены на отдельную страницу. Например, на рис. 4 собраны временнӹе графики изменения показателей двух сравниваемых 100-секундных разгонов: при углах наклона вектора β = 0° и β = 77.9°.
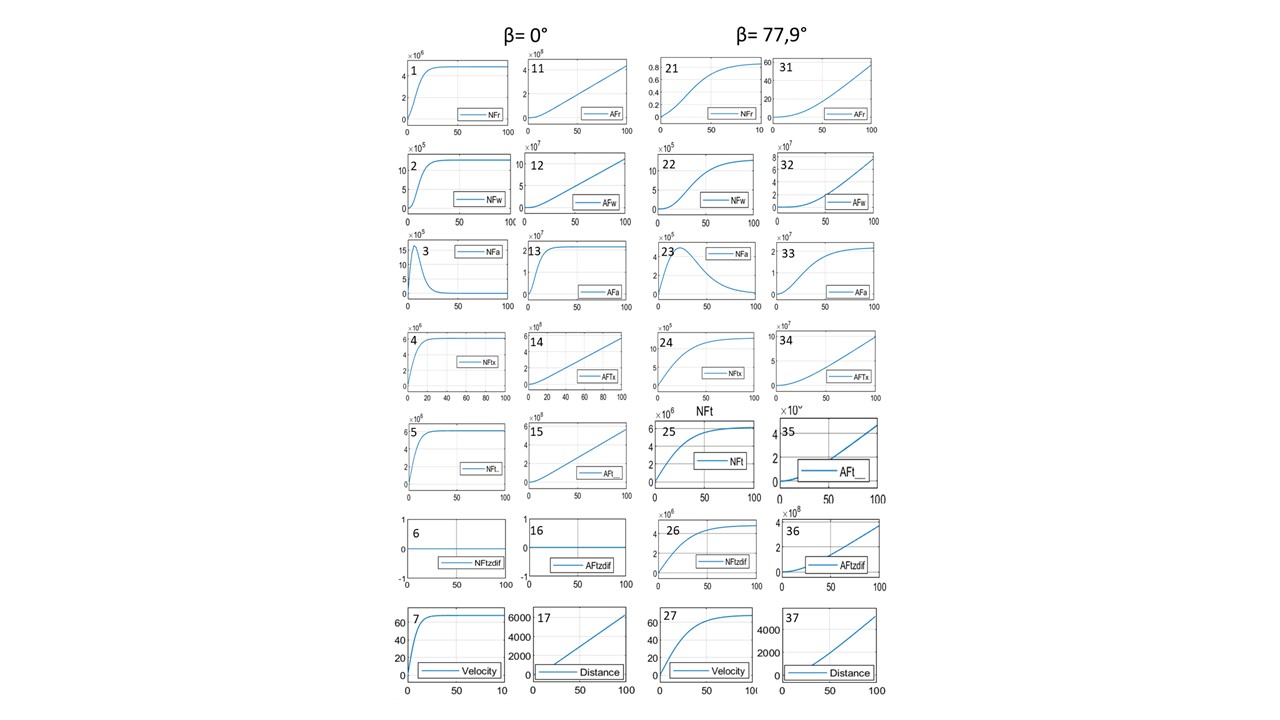
Рисунок 4 - Графики изменения показателей двух сравниваемых разгонов по ОП с fk0 = 0,3 до скорости 67,8 м/с при углах наклона вектора β = 0° (экспликации 1–7, 11–17) и β = 77.9° (экспликации 21–27, 31–37)
3. Основные результаты
3. Результаты расчета показателей движения квантомобиля
Для количественного исследования выбран гипотетический квантомобиль с данными автомобиля-аналога КамАЗ-4326 с КД (обоснован в , ):
Gq = 88000 H; fк0 = 0,3; fкV = 3,7×10–4 с2/м2; kв.x = cd×ρw/2 = 0,58 Н×c2/м4.
Посредством МПДК для демонстрации метода нашли нижеследующую пару ситуаций разгона до одной и той же скорости 67,8 м/с. Для этого привлекли трастовую характеристику скоростного среза (см. рис. 5).
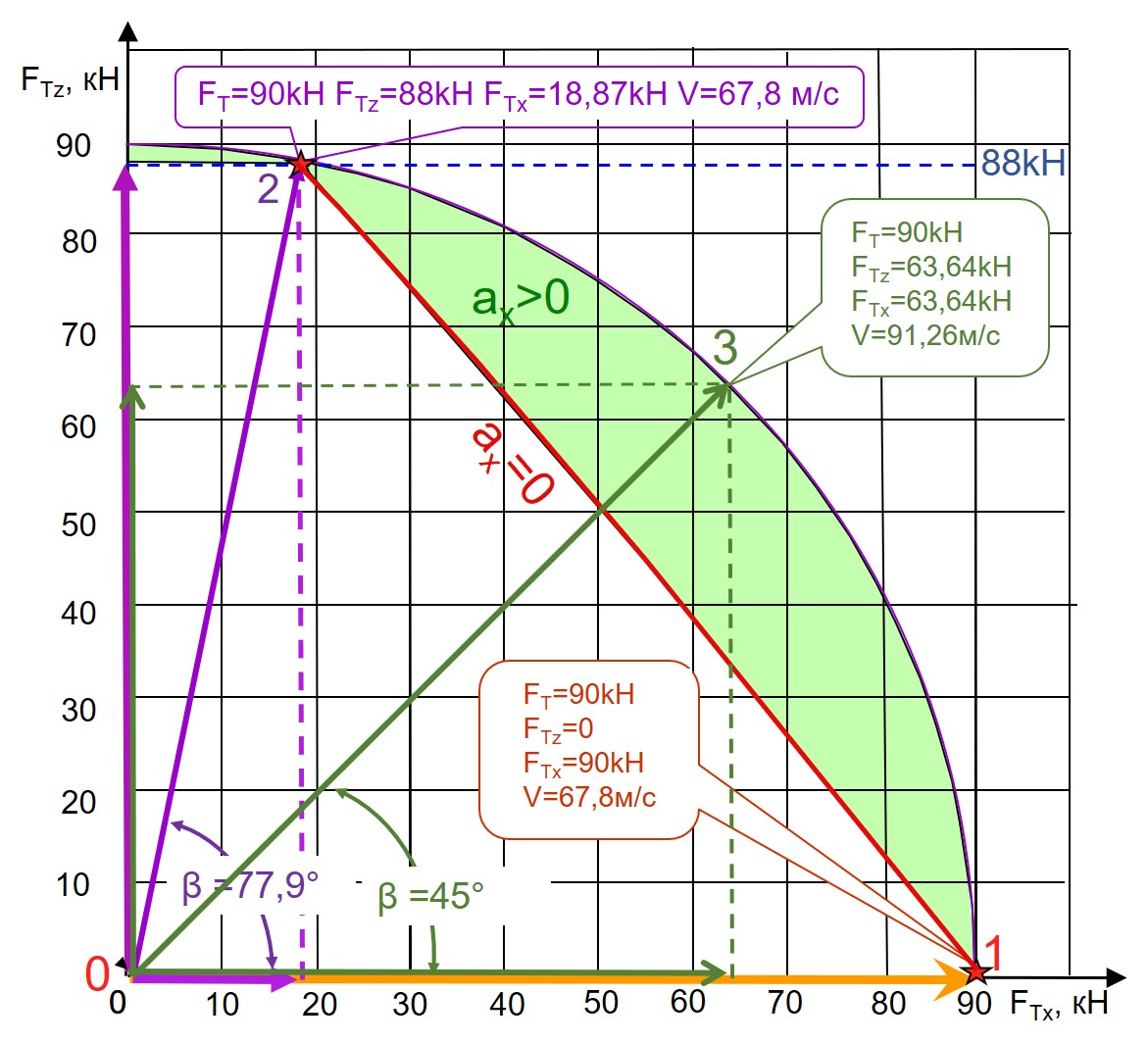
Рисунок 5 - Диаграмма использования траста величиной 90 кН в продольной плоскости тангажа при движении квантомобиля весом 88 кН по ОП с fк0 = 0,3
Примечание: трастовая характеристика скоростного среза [10]
При fк0 = 0,3 совершенно невывешенный экипаж (β = 0, FTz = 0 – точка 1 на рис. 5) достигнет максимальной скорости 67,8 м/с.
При угле βmax = 77,9° (точка 2 на рис. 5) FTz = 88 кН обеспечивает полное вывешивание без отлета экипажа, и при этом FTx = 18,87 кН. Тяговая сила FTx, идущая в этом случае только на преодоление сопротивления воздуха и сил инерции, позволяет разогнать экипаж до той же скорости 67,8 м/с.
Этим самым предоставляется возможность сравнения показателей движения, в том числе значений мгновенной мощности и накопленных энергозатрат, для двух крайних режимов движения:
1) только по ОП без какого-либо вывешивания;
2) только в воздухе (без касания ОП); – с достижением одного и того же результата – одинаковой максимальной скорости разгона Vmax (см. рис. 4).
Одинаковая скорость Vmax обеспечивает равенство приобретенной экипажем кинетической энергии Ek = AFa (см. на рис. 4 экспликации 13 и 33), что используем в дальнейших построениях методики.
Линейный характер зависимости сопротивления качению колес от изменения величины Gq' = (Gq–FTz) (см. уравнение (7)) определяет прямолинейный характер прямой 1-2 (на рис. 5), представляющей необходимую величину траста при изменяемом угле β для установившегося движения на скорости 67,8 м/с при fк0 = 0,3 . Зеленая зона на рис. 5 представляет пространство возможностей для дальнейшего разгона (ax > 0) – например, при β = 45° Vmax= 91,26 м/с (см. подробно в работе ). В данном случае энергообеспеченность вертикальной компоненты способствовало улучшению динамики движения квантомобиля.
Анализ рис. 4 и 5 позволяет оценить разницу в формировании показателей двух сравниваемых разгонов на временнóм лаге 100с до скорости Vmaxβ = 67,8 м/с.
На рис. 4 приведены показатели двух сравниваемых разгонов на лаге 100 с до скорости Vmaxβ = 67,8 м/с. Разгон при β = 0 более динамичен (см. мощности NFa на экспликациях 3 и 23, также графики скорости на экспликациях 7 и 27); кинетическая энергия AFa при β = 0 накапливается быстрее – за 30 c она достигает максимума, далее оставаясь постоянной (сравни графики 13 и 33). Но более высокие значения текущей скорости (в одних и тех же сечениях времени), однако, вызывают более высокие значения сил сопротивления воздуха Fw и соответствующей мощности NFw (сравни графики 2 и 22), приводя в процессе разгона к повышенным энергозатратам AFw на эту составляющую суммарных затрат энергии (сравни графики 12 и 32).
В табл. 2 приведены показатели трех разгонов на временном лаге 1000 с, позволяющие провести сравнительный анализ и расчет энергозатрат на лифт.
Таблица 2 - Показатели сравниваемых разгонов квантомобиля
№ | Показатель | Невывешенный ТС (β = 0°) | Частично вывешен ТС (β = 45°) | Вывешенный ТС (β = 77,9°) |
1 | Скорость Vmax, м/с | 67,8 | 91,26 | 68,17 |
2 | Путь S, м | 67 350 | 90 300 | 66 580 |
3 | Сила Fr, Н | 71312 | 29829 | 0,01266 |
4 | Сила Fw, Н | 18667 | 33812 | 18868 |
5 | Сила Fa, Н | 20 | 0 | 0 |
6 | Сила FTx, Н | 90000 | 63640 | 18868 |
7 | Сила FTz, Н | 0 | 63640 | 88000 |
8 | NFr, Вт / AFr, Дж | 4 835 528/ 4 788 696 248 | 2 722 154 / 2 678 043 385 | 0,8629 / 834 |
9 | NFw, Вт / AFw, Дж | 1 265 800 / 1 251 337 944 | 3 085 626 / 3 029 876 011 | 1 286 253 / 1 234 500 924 |
10 | NFa, Вт / AFa, Дж | 1 374 / 21 629 824 | 0 / 39 097 077 | 0 / 21 712 148 |
11 | NFTx, Вт /AFTx , Дж | 6 102 702 / 6 061 664 016 | 5 807 780 / 5 747 016 473 | 1 286 254 / 1 256 213 906 |
12 | NFT, Вт / AFT, Дж | 6 102 702 / 6 061 664 016 | 8 213 248 / 8 127 316 973 | 6 135 397 / 5 992 105 364 |
13 | NFTzdif, Вт / AFTzdif, Дж | 0 / 0 | 2 405 468 /2 380 300 499 | 4 849 143 / 4 735 891 459 |
14 | Knf_h, Вт/Н | nan | 37,8 | 55,1 |
15 | Kfn_h, Н/кВт | nan | 26,5 | 18,1 |
Примечание: FT = 90000 H, fк0 = 0,3, tr = 1000с
В табл. 2 и далее S, Fr, Fw, Fa – финальные значения пути и сил на отметке tr =1000 c; FTx и FTz – постоянные на всем лаге; NFr, NFw, NFa, NFTx, NFT, – финальные значения мощности, развиваемой соответствующими силами. NFTzdif = NFT – NFTx – разница значений мощности, развиваемой силой FT невывешенного экипажа и силой FTx вывешенного экипажа – всё для максимальной скорости; это потребная мощность реализации силы FTz, на базе которой формируется ЭЦВТ Knf_h = NFTzdif / FTz.
В табл. 2 и далее AFr, AFw, AFa, AFTx, AFT – значения работы, совершенной соответствующими силами силового баланса за время реализации tr. AFTzdif = AFT – AFTx = ∫0tr NFTzdif dt разница значений работы, совершаемой силой FT невывешенного экипажа и силой FTx вывешенного экипажа – всё на лаге tr; это работа силы FTz, совершенной в соответствии с искомой величиной показателя KNF_h.
Табл. 2 заполнялась данными с распечаток результатов ПИМ вида рис. 3. Для примера, конкретно данные с цифровых дисплеев рисунка 3 разместились в таблице в колонке β = 77,9° вывешенного ТС.
4. Обсуждение
Обсудим значения искомых величин и уровень возможных погрешностей.
Разница финальных значений мощности по преодолению сил сопротивления продольному движению экипажа для двух вариантов движения (строки 11–13 табл. 2):
NFTzdif = NFT – NFTx = 6 135 397 Вт – 1 286 254 Вт = 4 849 143 Вт.
Тогда ЭЦВТ для равенства энергоэффективности квантомобиля и автомобиля-аналога должен составлять: KNF_h = 4 849 143/88000=55,1Вт/Н.
Обратный ему коэффициент (в общепринятой размерности) KFN = 18,1 Н/кВт.
Другой вариант расчета – посредством средней мощности на лаге tr. Сравнение значений работы AFTx по преодолению сил сопротивления продольному движению экипажа в двух крайних вариантах (табл. 2 строка 11), позволяет выявить разницу совершаемой работы этих вариантов движения:
ΔAFTx(0–77.9°) = 6 061 664 016 – 1 256 213 906 = 4 805 450 110 Дж.
Средняя мощность на лаге 1000 с составляет 4 805 450 Вт. И тогда KNF_h = 4 805 450 /88000=54,6 Вт/Н.
Третий вариант расчета – по формуле (9): KNF_h = 67,8 (1–cos77,9°)/sin77,9° = 54,8 Вт/Н. Для скорости Vmax=68,17 м/с вывешенного ТС: KNF_h = 68,17 (1–cos77,9°)/sin77,9° = 55,1 Вт/Н.
Разница в полученных оценках KNF_h невелика. Она объясняется наличием погрешности в постановке численного эксперимента (наличие и проявление этапа разгона; Fa = 20 Н > 0, NFa = 1374 Вт – т.е. разгон за 1000 с не завершился; также Fr = 0,01266 > 0, NFr > 0 – не обеспечено абсолютное вывешивание при округлении значения FTz = 88 кН см. – точку 2 на рис. 5).
В качестве примера, относительно работы воздушных сил AFw (см. строки 9 и 12 табл. 2), разница составляет около 0,3% общей суммарной работы:
(100(1 234 500 924 – 1 251 337 944)/ 6 061 664 016 =0,277%)).
Эти погрешности – незначительны, их можно считать приемлемыми, тем более на фоне погрешностей численных процедур интегрирования и дифференцирования Matlab. В МПДК (для детального анализа сил, мощностей и работы) реализован первый вариант расчета – через NFTzdif.
Итак, сходные результаты разгонов (с одинаковыми конечной скоростью и накопленной кинетической энергией) обусловлены компенсацией физических факторов: работа сил сопротивления качению (при β = 0°) заменяется работой сил антигравитации (на осуществление лифта продолжительностью 1000 с. при β = 77,9°). То есть эффект устранения сопротивления качению по горизонтальной ОП как бы обеспечивается в каждый момент времени передачей мощности на поддержку вертикальной силы FTz..
Полученные количественные оценки можно принять за ориентиры в балансе составляющих энергозатрат квантомобиля: затраты на лифт экипажа должны характеризоваться величиной коэффициентов в лучшую сторону от полученных значений. Таким образом для рассмотренного примера относительно ЭЦВТ должно выполняться неравенство: KNF_h < 55,1Вт/Н.
Проведены расчеты ЭЦВТ KNF_h и ЭЦГТ KNF_l для четырех значений fk0 и четырех значений β – результаты (с округлением до целого) в табл. 3. Поскольку, как было отмечено выше, величина KNF_l имеет размерность скорости, то в табл. 3 в роли ЭЦГТ выступает скорость Vmax (именно с этой скоростью энергия передается от мобильного объекта в среду движения).
Таблица 3 - Значения граничной цены тяги (KNF = N/F, Вт/Н) в зависимости от коэффициента сопротивления качению fk0 и угла наклона вектора тяги β
Коэффициент сопротивления качению fk0 | Угол наклона вектора траста β, град | |||||||
Невывешенный ТС (β = 0°) | Вывешен частично (β = 15°) | Вывешен частично ТС (β = 45°) | Вывешен полностью (β = 77,9°) | |||||
Лифт (ЭЦВТ) | Вдоль (ЭЦГТ) | Лифт (ЭЦВТ) | Вдоль (ЭЦГТ) | Лифт (ЭЦВТ) | Вдоль (ЭЦГТ) | Лифт (ЭЦВТ) | Вдоль (ЭЦГТ) | |
0,3 | – | 68 | 10 | 77 | 38 | 91 | 55 | 68 |
0,2 | – | 83 | 12 | 83 | 41 | 100 | 55 | 68 |
0,1 | – | 105 | 15 | 112 | 46 | 111 | 55 | 68 |
0,01 | – | 146 | 19 | 142 | 51 | 124 | 55 | 68 |
Анализ результатов расчетов, собранных в табл. 3, позволяет отметить следующее. Диапазон значений цены горизонтальной тяги ЭЦГТ на движение конкретного исследованного ТС с максимальной для него скоростью (в рассмотренных условиях движения и при FT ≈ Gq) составил 68÷146 м/с. Диапазон значений требуемой цены вертикальной тяги ЭЦВТ на вывешивание ТС составил 0÷55 Вт/Н. При любой степени использования лифта цена вертикальной тяги оказалась ниже цены горизонтальной тяги (той же реализации плана эксперимента).
Теперь, использовав данные табл. 1, можно оценить место требований к КД со стороны ТС на фоне развивающегося технического направления – оно находится в середине ряда между реально существующими и прогностическими силовыми установками обеспечения лифта (примерно на уровне Винтокрылого носителя для воздушного старта ракет и геликоптеров – см. строки 4-6 табл.1 с учетом размерности).
5. Заключение
Разработанная в среде авторской Simulink-модели приземного движения квантомобиля (МПДК) подсистема Energetics позволила провести расчетное исследование формирования энергозатрат на этапах разгона и установившегося движения ТС. Эта модель, по мнению автора, может стать ядром алгоритмов расчета динамических и энергетических показателей произвольного движения квантомобиля.
На базе расчетов посредством МПДК преодолена познавательная сложность получения оценки реализуемой работы (энергозатрат) на вывешивание (лифт) экипажа. Неразрешимость (в рамках классической механики) расчета работы, совершаемой силой вертикального лифта при горизонтальном движении экипажа, – преодолена автором на основе идеи компенсации (перетока) энергии. Количество энергии, численно перемещаемой на ортогональное, вертикальное направление, равно разности между количеством совершаемой механической работы горизонтальных сил двух вариантов движения ТС: при отсутствии лифта и при полном вывешивании экипажа. Выигрыш от снижения сопротивления движению со стороны ОП при вывешивании экипажа сопровождается затратами энергии на поддержание лифта.
Величина ЭЦВТ KNF_h ≈ 55 Вт/Н носит весьма условный характер как минимум по двум причинам:
1) недостаточной широты полигона имитационного эксперимента;
2) отсутствия учета аэродинамической подъемной силы.
Тем не менее, по мнению автора, она позволила в первом приближении оценить порядок требований к энергообеспечению силовой тяги квантомобиля.
Классическая механика работает с изолированными, закрытыми системами. Развиваемая теория открытых систем , , одними из понятий которой являются понятия потоков энергии и мощности (которые, в частности, привлекаются к формализации извлечения энергии физического вакуума), по всей видимости, позволит в будущем охватить общими законами и рассмотренную в данной статье физическую особенность перетока энергии на ортогональные направления с привлечением категории Энергетическая цена тяги.
