Complanar Encounter of Two Space Vehicles in a Near-circular Orbit Using a Low Thrust Engine

В современных космических исследованиях достигнуты заметные успехи, особенно в отношении проведения встреч между космическими аппаратами (КА) на почти круговых орбитах с использованием двигателей малой тяги. Эта область исследований приобретает все большую актуальность благодаря множеству космических проектов, направленных на повышение точности и эффективности этих деликатных операций.

Успешная реализация встречи не только представляет собой сложную научно-техническую задачу в космонавтике, но и играет решающую роль в выполнении миссий по освоению космического пространства. Задачи встречи космических аппаратов могут различаться в зависимости от цели миссии, что делает их разнообразными по своим бизнес-целям.

В операциях сближения участвуют как минимум два КА, обычно один из которых выполняет маневры и полеты по свободной орбите – активный КА, в то время как другой остается пассивным. Это различие между активными и пассивными КА обеспечивает ясность и эффективность проводимых операций.

Задача встречи на околокруговой орбите с применением двигателей малой тяги имеет важное значение в практике полетов космических аппаратов (КА). Эта задача решается при сближении и стыковке КА, реализации группового полета нескольких КА, формирования заданной конфигурации спутниковых систем, а также при удалении космического мусора и обслуживании КА.

Еще с 60-х годов начался процесс использования на КА электрических ракетных двигателей (ЭРД). Благодаря высокому удельному импульсу ЭРД позволяют существенно снизить затраты топлива на орбитальное маневрирование. Однако малая (по сравнению с традиционными жидкостными ракетными двигателями) тяга ЭРД приводит к необходимости учета их длительной работы.

Однако задача оптимального маневрирования КА была рассмотрена в работах

За последние двадцать четыре года задача встречи была предметом изучения многих авторов

В настоящее время существует актуальная потребность в решении сложных задач маневрирования многоимпульсных космических аппаратов. Предложенные алгоритмы предоставляют возможность решения сложной задачи в несколько этапов: на первом этапе независимо друг от друга решаются задачи маневрирования в плоскости орбиты и поворота плоскости орбиты. Этот метод представлен в работах

На втором этапе принимаются численные методы, позволяющие находить оптимальное решение самых сложных многоимпульсных задач, учитывая широкий спектр ограничений

На третьем этапе, с применением решения задачи Ламберта, определяются параметры двухимпульсного решения задачи встречи. Затем происходит анализ поведения годографа базис-вектора, соответствующего найденному решению, и при необходимости добавляются некоторые дополнительные импульсы скорости, позволяющие достичь оптимального решения, как показано в

В данной статье представлен усовершенствованный алгоритм, обладающий замечательной способностью решать задачу встречи двух космических аппаратов на околокруговой орбите при низкой тяге. Указанное отличие особенно важно, поскольку некоторые алгоритмы не обеспечивают решений при использовании малых значений тяги. Однако благодаря внесенным модификациям удалось обнаружить эффективные решения, способствующие успешному выполнению маневров при низкой тяге. Фактически, в данной работе задача встречи рассматривается как в импульсной постановке, так и с учетом длительной работы двигателя малой тяги. Этот алгоритм более эффективен не только в наземных центрах управления, но и на борту космического аппарата, в отличие от предыдущих исследований

Для анализа относительного движения космических аппаратов в окрестности круговых орбит необходимо использовать специальные математические модели движения. Наиболее распространенной моделью относительного движения в окрестности круговых орбит является модель Hill-Clohessy-Wiltshire

С увеличением числа маневрирующих космических аппаратов и повышением оперативности решения задач возникает тенденция переноса процесса расчета маневров на борт КА. Это объясняется необходимостью упрощения процесса расчета параметров маневров и повышения надежности этого процесса. Рассматриваемый в данной работе алгоритм обладает этими характеристиками.

Задача расчета параметров маневров перелета между близкими околокруговыми орбитами решается в приближенной импульсной постановке, в рамках невозмущенного кеплеровского движения. Условия перелета с помощью N импульсов скорости за фиксированное время с исходной орбиты в заданную точку конечной компланарной орбиты (задача встречи) в линейном приближении могут быть выражены следующим образом

(1)

(2)

(3)

(4)

где , , , , , 

Здесь «f», «0» – индексы, соответствующие конечной и начальной орбитам, ef,e0 – эксцентриситеты орбит; аf,a0 – большие полуоси орбит; ωf,ω0 – углы между направлением на перицентр соответствующей орбиты и направлением на заданную на конечной орбите точку (ось Ох – направлена на эту точку); tf – необходимое время прихода в заданную точку, t0-время, в которое при движении по начальной орбите проекция радиус-вектора на плоскость конечной орбиты попадает на луч, проходящий через заданную точку встречи; V0,λ0 – орбитальная и угловая скорости движения по опорной круговой орбите радиуса r0 (r0=аf); N – число импульсов скорости; φi– угол приложения i-го импульса скорости, отсчитываемый от направления на заданную точку встречи в сторону движения КА; ,  – трансверсальная и радиальная составляющие i-го импульса скорости соответственно. Необходимо учитывать, что углы φi– отрицательны, т.к. было принято, что в заданной точке φf=0.

Задачу поиска параметров оптимальных маневров можно сформулировать следующим образом: необходимо определить ΔVri, ΔVti, φi (i=1,…,N), при которых суммарная характеристическая скорость маневров ΔV минимальна:

,

при ограничениях (1)-(4).

Предполагая, что импульсы скорости прикладываются в точках оптимальных для коррекции вектора эксцентриситета и угли приложения импульсов можно рассчитать по формулам:

,

Находим величины импульсов скорости оптимального решения при решении использовании первых трех уравнений системы (1)-(4):

(5)

(6)

Возможны три типа решений, для которых выполнены необходимые условия оптимальности:

а) на плоскости μ,λ годограф базис-вектора – эллипс, центр которого расположен на оси μ, но смещен от начала системы координат; эллипс касается окружности единичного радиуса в точке, лежащей на оси μ;

б) годограф базис-вектора вырождается в точку, совпадающую с точкой пересечения окружности единичного радиуса оси μ;

в) годограф базис-вектора - эллипс с центром в начале системы координат, касающийся окружности в двух точках на оси μ.

Так как у всех возможных оптимальных решений λ=0, а μ≠0, то импульсы скорости у этих решений чисто трансверсальные.

При решении задачи встречи величины импульсов скорости ΔVt1, ΔVt2, определенные при решении задачи перехода, распределяются между разрешенными для маневрирования N витками:

(7)

(8)

Здесь N число витков, на которых разрешено маневрирование.

Дальнейшая цель заключается в выборе такого распределения импульсов скорости вдоль витков, которое удовлетворяло бы уравнению (4). Для значительного упрощения решения задачи предполагаем, что величины импульсов скорости вдоль витков изменяются линейно:

(9)

(10)

Здесь ΔV1t1, ΔV1tN и ΔV2t1, ΔV2tN величины импульсов скорости на первом и последнем разрешенных витках маневрирования, являющиеся частью первого и второго импульса скорости решения задачи перехода.

Подставляя величины импульсов скорости, вычисленные по формулам (9), (10) в (7) и (8) получаем:

(11)

(12)

Используя (11) и (12), получаем формулы для определения ΔV1tN, ΔV2tN:

(13)

(14)

Подставив найденные величины ΔV1tN, ΔV2tN в формулы (9) и (10), получаем:

(15)

(16)

Таким образом, нашли значения всех импульсов скорости, выраженные только через ΔV1t1 и ΔV2t1. Подставляя их в уравнение (3), получаем линейное уравнение с двумя неизвестными ΔV1t1, ΔV2t1. Коэффициенты при импульсах скорости известны, так как известны их углы приложения:

(17)

(18)

Перебирая в заданных пределах значение переменной ΔV1t1, для каждого значения из уравнения (3) находим значение переменной ΔV2t1. Однако следует учесть направления скоростей: одна может разгоняться, а другая – тормозить, или наоборот, в зависимости от выполнения условия, представленного в формуле (4).

Затем, используя уравнения (15) и (16), вычисляем величины всех импульсов скорости. После чего, сложив модули всех импульсов скорости, находим суммарную характеристическую скорость для каждого решения. Решение, у которого суммарная характеристическая скорость минимальна, принимается в качестве оптимального варианта встречи. Если суммарная характеристическая скорость найденного решения совпадает с суммарной характеристической скоростью решения задачи перехода, то можно утверждать, что найдено решение с минимально возможной суммарной характеристической скоростью.

На следующем этапе производится оценка продолжительности каждого из найденных маневров.

Продолжительность каждого маневра оценивается с использованием следующего соотношения:

(19)

где wс – центростремительное ускорение опорной круговой орбиты , w – ускорение, создаваемое ДУ , m - масса активного КА, P – тяга его двигателя.

Если продолжительность самого большого импульса скорости не превышает 20°, то решение приближено к импульсному, и задачу считаем решённой. В случае значительной продолжительности маневров переходим к решению с использованием малой тяги.

Для каждого витка находим какие изменения эксцентриситета и большой полуоси производят импульсы скорости определенные на этом витке

(20)

(21)

Затем определяем нужную продолжительность маневров малой тяги, которые произведут такое же изменение этих элементов

(22)

Таким образом, мы находим продолжительность каждого маневра виток за витком. Задача с малой тягой успешно решена. В случае, если аргумент арксинуса превышает 1, решение невозможно (с учетом имеющейся тяги и массы космического аппарата для заданного числа витков).

Предыдущий алгоритм оказался недостаточным для решения задачи встречи космических аппаратов с двигателями малой тяги при малом числе витков и низкой тяге

1 – Задать начальные значения параметров и переменных.

2 – Решение задачи перехода между компланарными орбитами: используя уравнения 5 и 6, вычислить две величины импульсов скорости.

3 – Решение задачи встречи: распределить величины импульсов скорости по N виткам, удовлетворяя условиям времени с помощью уравнений 15, 16 и 4. Пересчитывать значения импульсов на каждом витке при необходимости, учитывая алгебраические вычисления.

4 – Определение изменения эксцентриситета и большой полуоси: рассчитать изменение эксцентриситета и большой полуоси на каждом витке, как в предыдущем алгоритме.

5 – Учет продолжительности маневров: используя уравнение 22, учитывать продолжительность маневров. Если решение еще не достигнуто, вернуться к шагу 3; в противном случае перейти к следующему шагу.

6 – Расчёт общих затрат: используя уравнение 19, можно рассчитать общие затраты. 

Найденное решение с «малой тягой» демонстрирует аналогичное изменение большой полуоси и вектора эксцентриситета, что и исходное импульсное решение. Уравнение (4) выполняется достаточно точно, поскольку середины продолжительных маневров совпадают с моментами приложения импульсов скорости. Это также приводит к аналогичному изменению большой оси на витке, обеспечивая необходимое время прибытия в точку встречи.

Однако при решении задачи встречи были использованы линеаризованные уравнения движения, не учитывающие нецентральность гравитационного поля, влияние атмосферы и т.д. Это приводит к тому, что реальная точность выполнения терминальных условий в системе (1)-(6) оказывается недостаточной. В связи с этим для решения задачи с требуемой точностью может быть целесообразным использование итерационной схемы

Рассмотрим движение космического аппарата (КА) относительно точки O, движущейся по невозмущенной околокруговой орбите радиусом 6871 км. Гравитационный параметр Земли примем равным 3,9860044∙1014 м3/с2. Рассмотрим задачу перелета с помощью N импульсов скорости за фиксированное время с исходной орбиты в заданную точку конечной орбиты из точки фазового пространства r0 = (10; 100; -5) км, v0 = (1; -10; 3) м/c в начало координат, то есть в точку rf = (0; 0; 0) км, со скоростью vf = (0; 0; 0) м/c. Для задачи начальную массу КА примем равной 1000 кг, удельный импульс двигательной установки КА – 220 секунд (2157,463 м/с), а тягу (T) будем варьировать в диапазоне от 0,362 до 100 Н. Перелет осуществляется за N=4.

В таблице 1 приведены результаты расчетов параметров двух-импульсного перехода между компланарными орбитами, углы приложения первого и второго импульса, которые будут использоваться как начальные приближения для решения задачи встречи.

Как видно, при решении задачи перехода были получены два импульса скорости, один разгоняющий и другой тормозящий, и де-факто, минимальная величина характеристической скорости, которую должен иметь КА для маневра перехода, составляет 4,485 м/с.

После перебора первого импульса скорости в границах от -2,785м/с до 0,5 м/с с шагом 0,025 м/с получаются параметры оптимальных решений, представленные на рисунках 1 и 2.

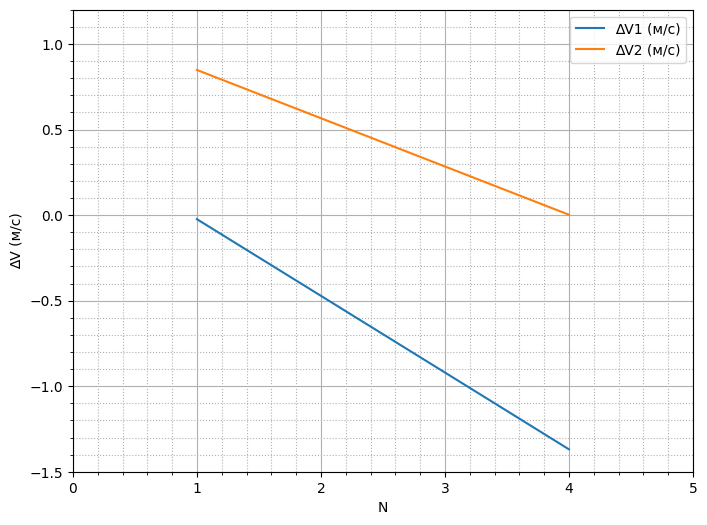
Рисунок 1 - Параметры оптимального решения при N=4

DOI:10.23670/IRJ.2024.142.155.2

Как видно, при уменьшении тяги (на малых витках), продолжительность нескольких импульсов возрастает более, чем необходимо для коррекции эксцентриситета. Для ограничения продолжительности этих импульсов мы устанавливаем их амплитуду на уровне, когда они всё ещё существенно влияют на эксцентриситет, но максимально уменьшаем их количество. Этот подход проиллюстрирован на рисунке 2, где изменения величины импульсов имеют свободную форму, обеспечивая правильную коррекцию эксцентриситета, чтобы в свою очередь определить оптимальную продолжительность этих импульсов.

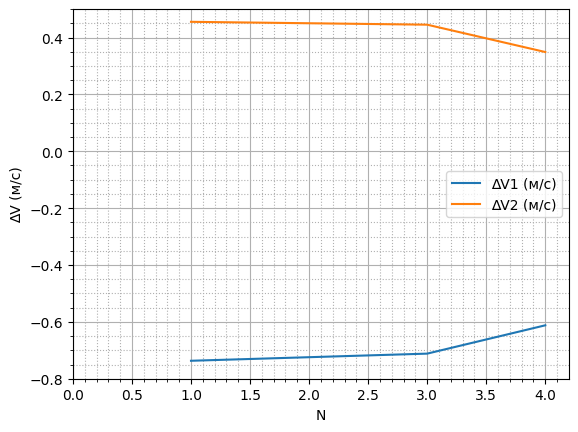
Рисунок 2 - Параметры оптимального решения при N=4

DOI:10.23670/IRJ.2024.142.155.3

Далее рассмотрим решение задачи с малой тягой. В таблицах 2, 3, 4 и 5 представлены результаты расчетов задачи встречи с малой тягой при условии «Тяга = 0,362Н», при N=4.

В некоторых случаях решений не существует из-за того, что значения аргумента арксинуса выходят за пределы диапазона (-1; 1). Поэтому в таблице 2, в интервале от 0,362 до 0,5 Н, решение отсутствует из-за несуществования арксинуса. Однако, в таблице 3, очевидно, что решения существуют при низких значениях тяги.

В таблицах 4 и 5 представлены распределения импульсов скоростей и продолжительности маневров в зависимости от числа витков.

Как можно заметить из таблицы 4, решения имеются только на первом и втором витках, в то время как на остальных витках их отсутствует, в соответствии с нашими предыдущими доказательствами.

В таблице 5 представлены результаты расчета задачи с малой тяги, в которой, в свою очередь, решения имеются на всех 4-х витках.

При увеличении тяги продолжительности маневров уменьшаются, затраты суммарной характеристической скорости (СХС) решения с малой тяги при увлечении тяги совпадают с затратами СХС импульсного решения.

В рассматриваемом в данной работе алгоритме расчета параметров двухимпульсной встречи на околокруговой орбите выявляется его ключевое преимущество – простота и надежность. Эти качества позволяют применять алгоритм не только в наземных центрах управления, но и на борту космического аппарата. Одновременно с этим предложенный алгоритм демонстрирует способность получать оптимальное решение в тех случаях, когда начальная фаза принадлежит оптимальному фазовому диапазону, а суммарная характеристическая скорость встречи совпадает с суммарной характеристической скоростью оптимального решения задачи перехода. Этот алгоритм эффективен даже в случаях, когда маневры выполняются двигателями малой тяги. Приведенные в работе примеры подтверждают высокую работоспособность и качество полученного решения, а также его применимость для решения практических задач. Предложенный модификационный алгоритм открывает новые перспективы и более эффективные алгоритмы для космических миссий с использованием космических аппаратов с ограниченной тягой, что является значимым шагом в развитии космической навигации.