Energy Levels of Electrons in a Magnetic Field and the Integer Quantum Hall Effect

Как известно, в современной квантовой физике энергетические уровни электронов при их движении по циклотронным орбитам (т.е. по окружностям) в магнитном поле без учёта спиновой степени свободы электронов находятся в соответствии с формулой (1) (см. также

(1)

где, ( – постоянная Планка);

– угловая частота движения электрона по циклотронной орбите;

- принимает значения 0, 1, 2, 3, 4 и т.д.

Формула (1) была впервые получена Л. Д. Ландау в 1930 году как решение уравнения Шрёдингера для электрона в магнитном поле

У всех металлов наблюдается специфическая осцилляционная зависимость магнитного момента (эффект де Гааза – ван Альфена), сопротивления (эффект Шубникова – де Гааза), теплоёмкости и других характеристик от магнитного поля

Сравнительно недавно группе американских учёных из Физической школы Технологического института Джорджии (Атланта, США) совместно с коллегами из Центра наноразмерных систем и технологий Национального института стандартов и технологий (Гейтерсберг, Мэриленд, США) удалось пронаблюдать около 20 уровней Ландау в графене

Необходимо однако подчеркнуть, что в указанных выше экспериментах обнаружено именно квантование энергии заряженных частиц в магнитном поле. При этом точное подтверждение формулы (1), согласно современным физическим представлениям, связано с большими трудностями, так как «… в реальных … системах, в циклотронную частоту  входит эффективная масса электрона … циклотронная эффективная масса может отличаться от массы свободного электрона …»

Кроме того, в графене при энергия квазичастиц равняется нулю даже в присутствии магнитного поля

Целью данной работы является проверка соответствия формулы (1) экспериментальным зависимостям холловского сопротивления  в функции от значения магнитной индукции  () и напряжения на затворе МОП – транзистора  в явлении целочисленного квантового эффекта Холла при значении массы электрона, равной его массе покоя.

Проверка справедливости формулы (1) в данной работе будет проводиться без использования понятия эффективной массы, масса электрона будет принята равной массе покоя. Для обоснования правомерности такого подхода автором в данной статье из формулы де Бройля без учёта спиновой степени свободы выведена формула (11) для величин энергетических уровней электронов, двигающихся по циклотронным орбитам в магнитном поле. Оказывается, что формула (11) не совпадает с формулой (1). Как будет показано в дальнейшем, формула (11) и, следующая из неё формула (22), при принятии значения массы электрона равной массе покоя, соответствует экспериментальным зависимостям холловского сопротивления  в функции от значения магнитной индукции  и напряжения на затворе МОП – транзистора  в явлении целочисленного квантового эффекта Холла (ЦКЭХ), а формула (1), при принятии значения массы электрона, равной массе покоя, не согласуется с указанными экспериментальными зависимостями. Формула (11) показывает, что нет необходимости обращаться к понятию эффективной массы и спина электрона при проверке соответствия формул (1) и (11) экспериментальным зависимостям  и  в явлении ЦКЭХ. Несоответствие формулы (1) экспериментальным зависимостям  и  при принятии массы электрона, равной массе покоя, может иметь большое значение для понимания физических процессов, происходящих в полупроводниках при ЦКЭХ.

Исходя из формулы де Бройля можно совершенно непротиворечиво показать, что энергетические уровни электронов при их движении по циклотронным орбитам в магнитном поле без учёта спиновой степени свободы электронов могут быть найдены по формуле, отличающейся от (1).

Допустим, что электрон движется поступательно в пространстве, свободном от действия магнитного поля. В некоторый момент времени включается магнитное поле, силовые линии которого перпендикулярны вектору скорости электрона. Очевидно, что в этом случае под действием силы Лоренца электрон начнёт двигаться по циклотронной орбите в плоскости, перпендикулярной магнитному полю. Так как направление силы Лоренца перпендикулярно вектору скорости электрона, то работа, совершаемая ею, равна нулю и механическая энергия электрона в магнитном поле, без учёта спиновой степени свободы электрона, будет равна его кинетической энергии движения по циклотронной орбите, поэтому кинетическая энергия является также и энергией уровня электрона в рассматриваемом случае.

Запишем формулу де Бройля для электрона, двигающегося по циклотронной орбите в магнитном поле, и преобразуем её к виду (4):

(2)

(3)

(4)

В формулы (2 – 4) входят следующие обозначения:

– длина волны де Бройля электрона при его движении по циклотронной орбите в магнитном поле;

– масса покоя электрона;

– поступательная скорость движения электрона по циклотронной орбите;

– кинетическая энергия электрона;

– время прохождения электроном расстояния вдоль циклотронной орбиты, равного длине волны де Бройля электрона.

Радиус окружности (циклотронной орбиты) электрона в магнитном поле в рассматриваемом случае определяется соотношением (5)

(5)

Период обращения электрона в однородном магнитном поле

(6)

Известно, что квантовым условием устойчивости круговой орбиты электрона является целое число волн де Бройля, укладывающихся на данной орбите

(7)

где  – целое положительное число, принимающее значения 1, 2, 3, 4 и т.д.

Запишем  в (7) в соответствии с (5) и значение  в соответствии с (6):

(8)

где,  – радиус -ой циклотронной орбиты.

Далее

(9)

(10)

Из соотношения (10) следует, что при радиусы  циклотронных орбит электрона могут принимать только дискретный ряд значений, соответствующих значениям и т.д.

Из дискретности значений радиусов  следует и дискретность изменения кинетической энергии электронов при переходе электрона с одной циклотронной орбиты с одним значением радиуса на другую орбиту с другим значением радиуса, но тем же центром вращения. 

В соответствии с формулой (7) дискретные значения кинетической энергии электрона , которую в дальнейшем будем обозначать как энергию уровня  (так как, как было отмечено выше, кинетическая энергия электрона в рассматриваемом случае является также и энергией уровня) будут определяться соотношением (11):

(11)

где, ;

 – угловая частота движения электрона по циклотронной орбите.

Сравнение (11) и (1) показывает, что значению  в (11) соответствует значение  в (1), т.е. минимально возможные уровни энергии электронов в магнитном поле, определяемые по формулам (11) и (1), совпадают и записываются в виде

(12)

где, - уровень энергии электронов в магнитном поле при их движении по циклотронным орбитам при  (формула (11)) и  (формула (1)).

Для всех других уровней энергии электронов в магнитном поле при их движении по циклотронным орбитам уровни энергии, определяемые по формулам (11) и (1), не совпадают, при этом расстояние по энергии между ближайшими уровнями, определяемыми по формуле (11), находится согласно соотношению

(13)

а расстояние по энергии между ближайшими уровнями, определяемым по формуле (1), находится согласно соотношению

(14)

Другими словами, энергетический спектр электронов в магнитном поле, определяемый по формуле (11), в два раза плотней (его энергетические уровни расположены по энергии в два раза гуще), чем энергетический спектр, определяемый в соответствии с формулой (1). Казалось бы формула (1), как общепринятая в современной квантовой физике, однозначно верна, а формула (11) ошибочна, однако прошу читателя не торопиться с выводами. Энергетический спектр атома водорода, как это не трудно проверить, может быть рассчитан в соответствии с формулой (11), а ведь энергетический спектр водорода надёжно проверен экспериментально. Разумеется, что при этом в формуле (11) под  надо понимать угловую частоту вращения электрона по круговой орбите в атоме водорода, а под  – абсолютное значение энергии уровня. В атоме водорода модели Бора абсолютное значение энергии уровня электрона равно значению его кинетической энергии движения по круговой орбите вокруг ядра атома.

Покажем, что использование формулы (11) позволяет получить формулу для энергии уровня в атоме водорода (без учёта тонкой структуры и спина):

(15)

где,  

.

Соотношение (15), объединённое с формулой, определяющей первый постулат Бора, позволяет получить одну из фундаментальных физических констант – постоянную Ридберга.

Кроме этого, в разделе 5 данной статьи будет показано соответствие формул (11) и (13) экспериментальным зависимостям холловского сопротивления  в функции от индукции магнитного поля и от напряжения на затворе МОП – транзистора в целочисленном квантовом эффекте Холла (ЦКЭХ) и противоречие формул (1) и (14) указанным экспериментальным зависимостям. 

Без учёта спина на одно квантовое состояние электрона, как это следует из (10), должна приходиться площадь:

(16)

Величину  в (16) принято называть магнитной длиной и обозначать  

(17)

В данном случае важно, что значение магнитной длины  получено на основании уравнения (7) без решения уравнения Шрёдингера.

Из соотношения (5) следует, что импульс электрона при его движении по циклотронной орбите с радиусом  в скалярной форме может быть записан в виде

(18)

Из (18) и (9) непосредственно следует

(19)

Способ получения соотношения (19), изложенный в данной статье, позволяет показать, что второй постулат Бора (правило квантования орбит) справедлив не только по отношению к движению электрона по круговым орбитам в атоме водорода, но и по отношению к движению электрона по циклотронным орбитам в магнитном поле, перпендикулярном плоскости циклотронных орбит электронов. В современной физике вопрос о квантовании момента импульса электрона в соответствии со вторым постулатом Бора при его движении по циклотронным орбитам в плоскости, перпендикулярной магнитному полю, не рассматривается.

С использованием соотношений (19) и (10) нетрудно получить формулу для величины скорости движения электрона по квантованным циклотронным орбитам в плоскости, перпендикулярной магнитному полю:

(20)

С учётом (20) длина волны да Бройля электрона на -ой циклотронной орбите  запишется в виде

(21)

Используя соотношения (11) и формулы (10) и (20), запишем энергию уровня электрона в виде

(22)

где,  – магнетон Бора;

 – целое положительное число, принимающее значения 1, 2, 3, 4 и т.д.

«Энергетическая щель» между ближайшими уровнями энергии в рассматриваемом случае в согласии с (13) будет определяться выражением

(23)

В данном случае важно подчеркнуть, что соотношения (22) и (23) следуют из соотношения (11) и формул (10) и (20), строго выведенных из формулы де Бройля (2).

Из формулы (1) с помощью известной формулы  

(24)

где,  принимает значения 0, 1, 2, 3, 4 и т.д.

«Энергетическая щель» между ближайшими уровнями энергии, согласно формуле (24), определяется выражением

(25)

Необходимо отметить, что формулы (22), (23), (24) и (25) получены при значении массы электрона, равной массе покоя.

В дальнейшем в разделе 5данной статьи будет показано соответствие формул (22) и (23) экспериментальным зависимостям холловского сопротивления  в функции от индукции магнитного поля и от напряжения на затворе МОП - транзистора в явлении ЦКЭХ и противоречие формул (24) и (25) указанным экспериментальным зависимостям.

Рассмотрим теперь в соответствии с формулами (22) и (23) порядок заполнения электронами энергетических уровней при плавном понижении индукции магнитного поля B. Обратимся к рассмотрению рис. 1а. На этом рисунке вдоль вертикальной оси откладывается величина энергии электростатического поля затвора или гетероструктуры, приходящаяся на один электрон (удельная энергия) (где – потенциал электростатического поля затвора – подложки или гетероструктуры в двумерном электронном газе (2МЭГ), т.е. в зоне проводимости). Выше нулевой отметки проведена горизонтальная линия, соответствующая удельной энергии , в рассматриваемом случае она является постоянной величиной, так как постоянным является напряжение на затворе . На рис. 1б вдоль вертикальной оси в соответствии с формулами (22) и (23) откладываются величины дискретных энергетических уровней, возникающих в 2МЭГ под действием магнитного поля с индукцией . Магнитное поле перпендикулярно плоскости 2МЭГ. 

Напряжение на затворе подобрано таким образом, что выполняется равенство (26) (см. также рис. 1б):

(26)

Так в 2МЭГ в зоне проводимости магнитное поле создаёт дискретный энергетический спектр, то электроны могут находиться в зоне проводимости только в том случае, когда они получают от электростатического поля затвора – подложки или от электростатического поля гетероструктуры количество энергии, достаточное для занятия данного энергетического уровня. Равенство (26) как раз и показывает, каким количеством энергии должен обладать один электрон, чтобы он мог занять место в 2МЭГ в зоне проводимости на энергетическом уровне  При понижении величины индукции магнитного поля с величины  спектр энергетических уровней на рис. 1б опускается вниз, но электроны в 2 МЭГ в зоне проводимости не смогут занять энергетический уровень  до тех пор, пока не будет выполняться равенство (27):

(27)

Из формулы (22) следует, что . Спектр энергетических уровней, соответствующий уравнению (27), показан на рис. 1в. Из (26) и (27) следует, что

(28)

(29)

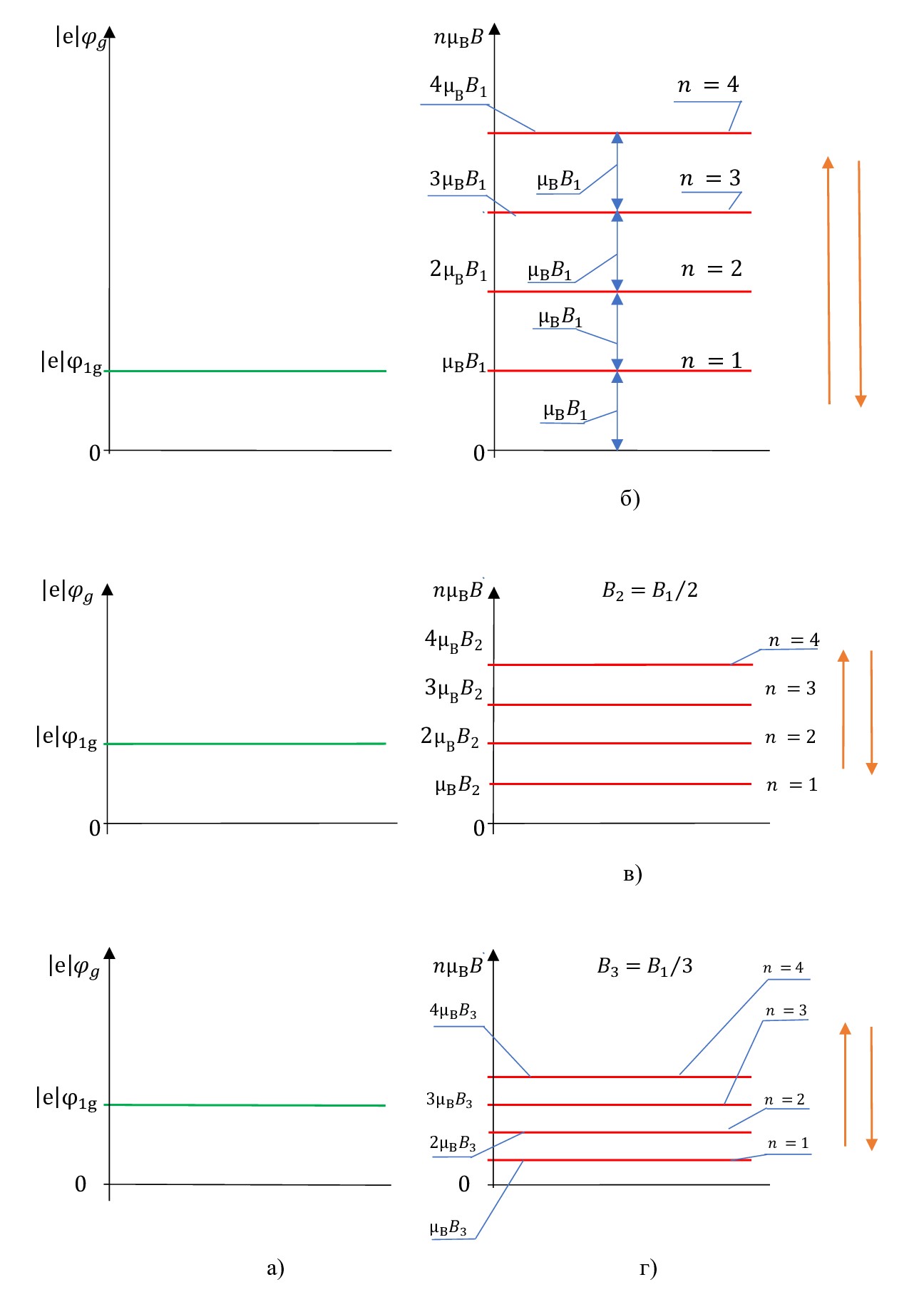
Рисунок 1 - Схематично показана связь между плавным изменением индукции магнитного поля B и постоянным значением потенциала φ1g электростатического поля затвора-подложки в зоне проводимости, умноженным на абсолютную величину заряда электрона |e|:

а - значение потенциала φ1g электростатического поля затвора-подложки в зоне проводимости, умноженного на абсолютную величину заряда электрона |e|; б, в, г - изменение индукции магнитного поля B

Примечание: номера энергетических уровней n даны в соответствии с формулой (22)

DOI:10.23670/IRJ.2023.129.38.1

При понижении величины индукции магнитного поля с величины спектр энергетических уровней на рис. 1в опускается вниз, но электроны в 2 МЭГ в зоне проводимости не смогут занять энергетический уровень до тех пор, пока не будет выполняться равенство (30):

(30)

Из формулы (22) следует, что . Спектр энергетических уровней, соответствующий уравнению (30), показан на рис. 1г. Из (30) и (26) следует, что

(31)

(32)

Аналогично при дальнейшем понижении индукции до величин  и  будут справедливы соотношения

(33)

(34)

Общим условием нахождения электронов на каком – либо энергетическом уровне является соотношение

(35)

Теперь можно построить теоретическую зависимость холловского сопротивления  в функции от . Известно, что холловское сопротивление  в случае ЦКЭХ находится по формуле (36)

(36)

где,  – целочисленный фактор заполнения, указывающий число полностью заполненных энергетических уровней в 2МЭГ.

При использовании формул (22) и (23) числу  соответствует полностью заполненный электронами энергетический уровень , числу  соответствует полностью заполненный уровень , числу  соответствует полностью заполненный уровень  и т.д.

Используя соотношения (29), (32), (33), (34) и формулу (36) можно построить в рассматриваемом случае теоретическую зависимость , которая показана на рис. 2. Плато холловского сопротивления  между точками 1 и 2, 3 и 4, 5 и 6 и т.д. появляется как следствие того, что число  полностью заполненных энергетических уровней изменяется при дискретном энергетическом спектре в магнитном поле в 2МЭГ теоретически только при определённых значениях индукции . Соответственно и холловское сопротивление  в согласии с формулой (36) также изменяется только при определённых значениях индукции , при постоянном значении числа  сопротивление  не изменяется, поэтому в интервалах между значениями индукции  и ,  и ,  и  и т.д. сопротивление  находится на плато.

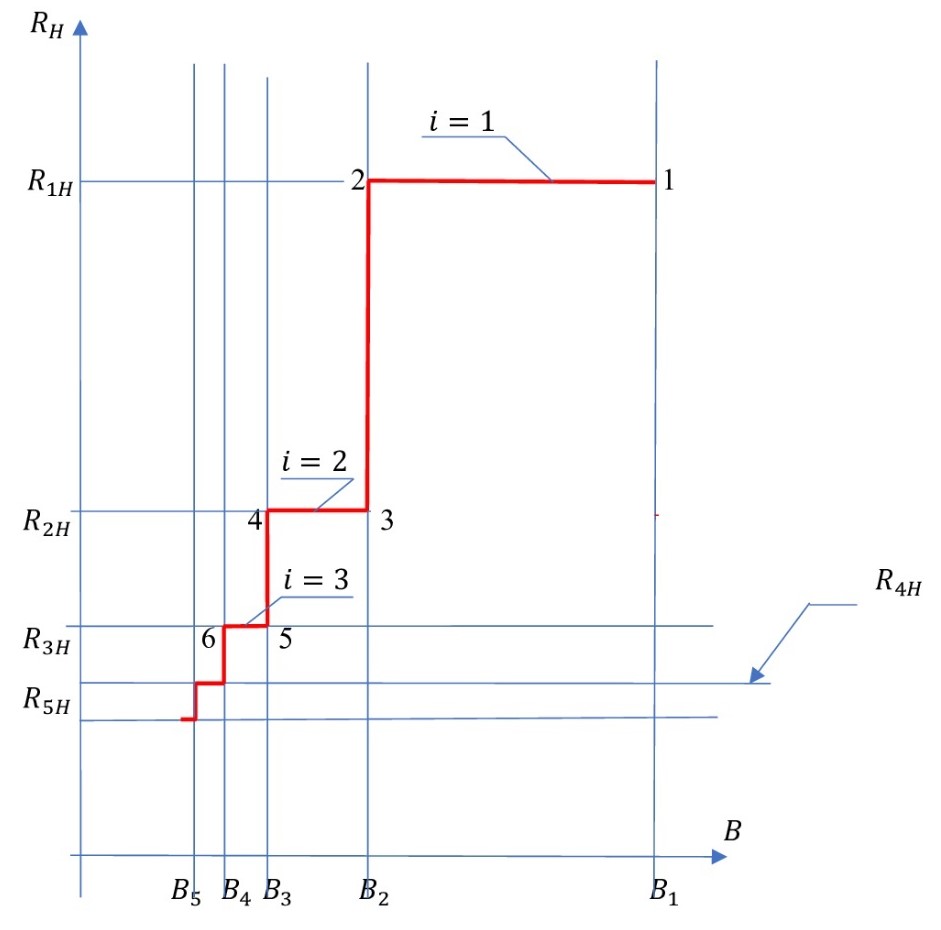
Рисунок 2 - График теоретической зависимости холловского сопротивления RH от значения магнитной индукции в образце B

Примечание: при использовании формул (22) и (23)

DOI:10.23670/IRJ.2023.129.38.2

Рассмотрим теперь в соответствии с формулами (24) и (25) порядок заполнения электронами энергетических уровней при плавном понижении индукции магнитного поля . При этом необходимо учитывать, что при использовании формул (24) и (25) числу соответствует полностью заполненный электронами энергетический уровень , числу соответствует полностью заполненный уровень , числу соответствует полностью заполненный уровень и т.д.

Обратимся к рассмотрению рис. 3а. На рисунке 3а вдоль вертикальной оси так же как и на рис. 1а откладывается величина энергии электростатического поля затвора или гетероструктуры, приходящаяся на один электрон (удельная энергия)  (где  – потенциал электростатического поля затвора – подложки или гетероструктуры в 2МЭГ, т.е. в зоне проводимости).

Выше нулевой отметки проведена горизонтальная линия, соответствующая удельной энергии , в рассматриваемом случае она является постоянной величиной, так как постоянным является напряжение на затворе . На рис. 3б вдоль вертикальной оси в соответствии с формулами (24) и (25) начиная с энергетического уровня  откладываются величиныдискретных энергетических уровней, возникающих в 2МЭГ под действием магнитного поля с индукцией . Магнитное поле перпендикулярно плоскости 2МЭГ.

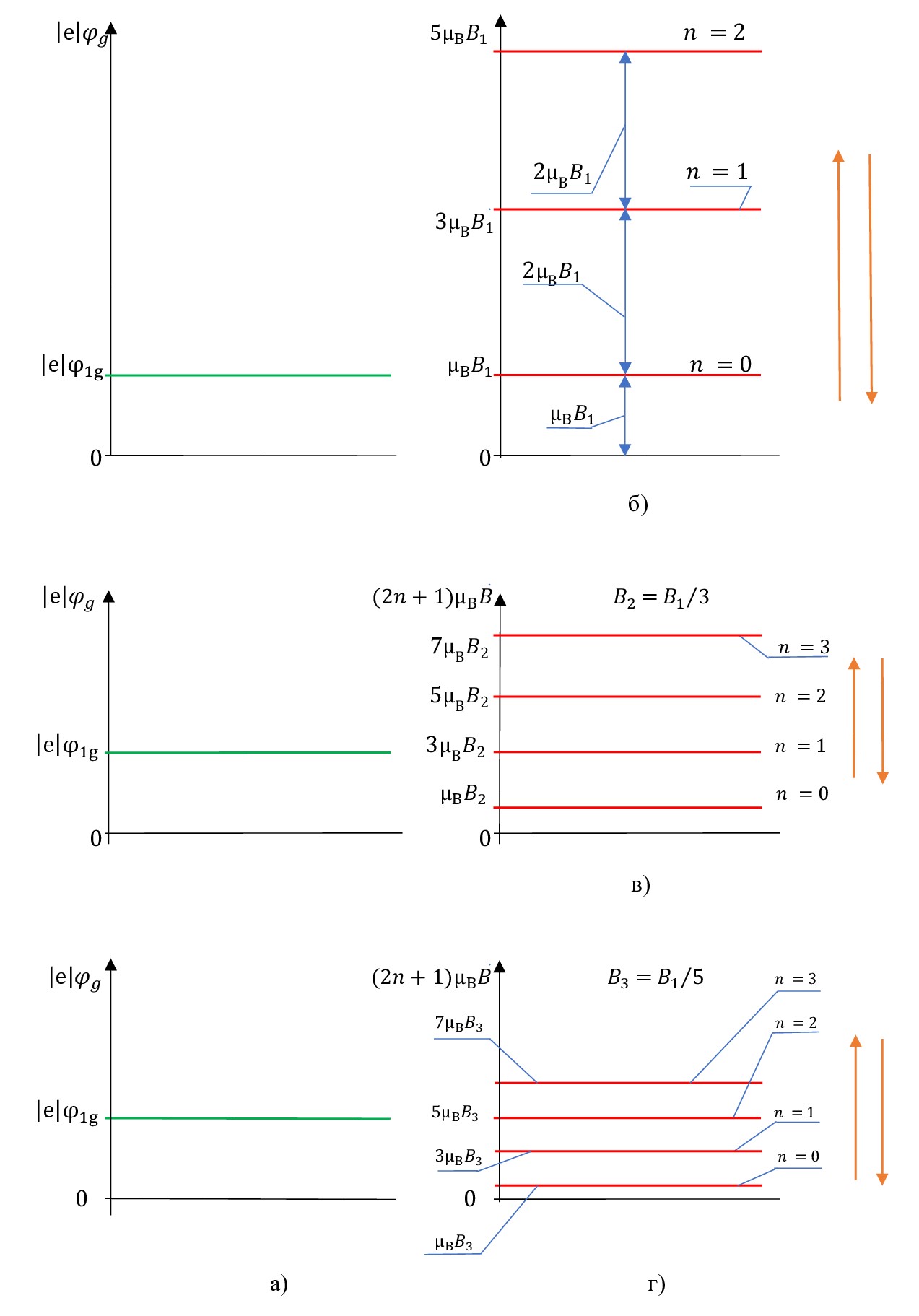
Рисунок 3 - Схематично показана связь между плавным изменением индукции магнитного поля B и постоянным значением потенциала φ1g электростатического поля затвора-подложки в зоне проводимости, умноженным на абсолютную величину заряда электрона |e|:

а - значение потенциала φ1g электростатического поля затвора-подложки в зоне проводимости, умноженного на абсолютную величину заряда электрона |e|; б, в, г - изменение индукции магнитного поля B

Примечание: номера энергетических уровней n даны в соответствии с формулой (24)

DOI:10.23670/IRJ.2023.129.38.3

Напряжение на затворе  подобрано таким образом, что выполняется равенство (37) (см. также рис. 3б):

(37)

При понижении величины индукции магнитного поля с величины  спектр энергетических уровней на рис. 3б опускается вниз, но электроны в 2 МЭГ в зоне проводимости не смогут занять энергетический уровень  до тех пор, пока не будет выполняться равенство

(38)

Из формулы (24) следует, что . Спектр энергетических уровней, соответствующий уравнению (38), показан на рис. 3в. Из (37) и (38) следует, что

(39)

(40)

При понижении величины индукции магнитного поля с величины  спектр энергетических уровней на рис. 3в опускается вниз, но электроны в 2 МЭГ в зоне проводимости не смогут занять энергетический уровень  до тех пор, пока не будет выполняться равенство

(41)

Из формулы (24) следует, что . Спектр энергетических уровней, соответствующий уравнению (41), показан на рис. 3г. Из (41) и (37) следует, что

(42)

(43)

Аналогично при дальнейшем понижении индукции до величин  и  будут справедливы соотношения

(44)

(45)

Используя соотношения (40), (43), (44), (45) и формулу (36) можно построить в рассматриваемом случае теоретическую зависимость , которая показана на рис. 4. Плато холловского сопротивления между точками 1 и 2, 3 и 4, 5 и 6 и т.д. появляется как следствие того, что число полностью заполненных энергетических уровней изменяется при дискретном энергетическом спектре в магнитном поле в 2МЭГ теоретически только при определённых значениях индукции . Соответственно и холловское сопротивление в согласии с формулой (36) также изменяется только при определённых значениях индукции .

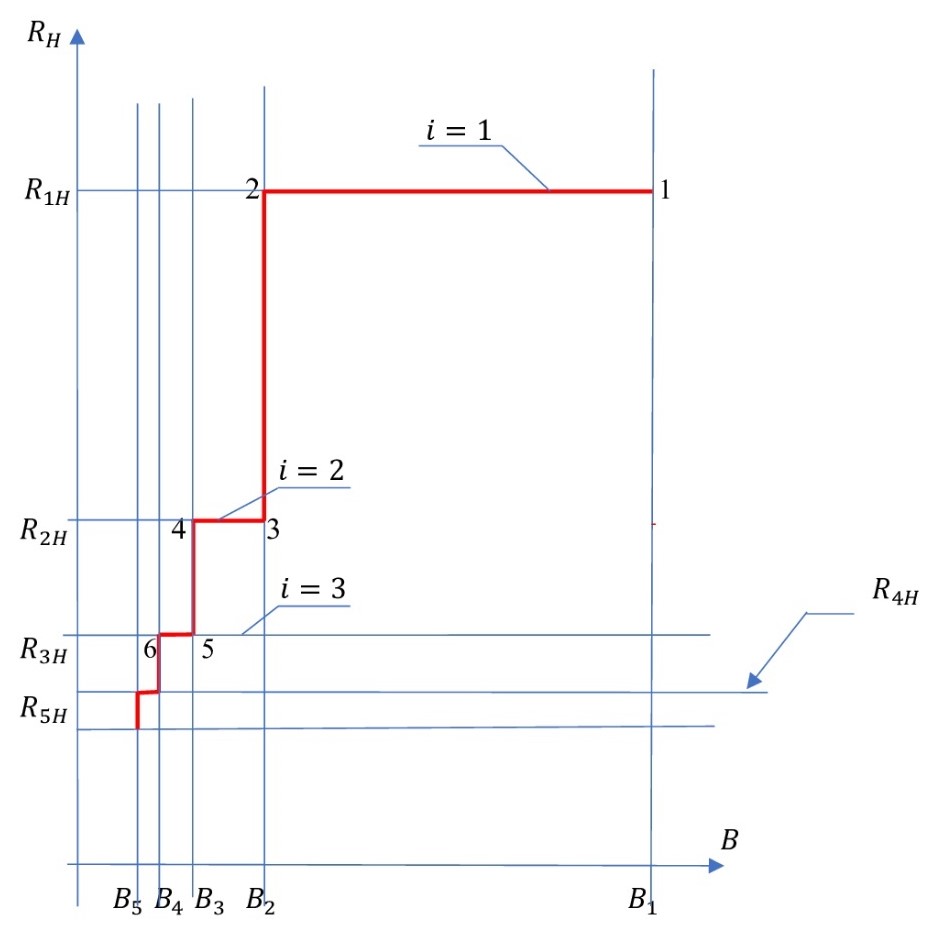
Рисунок 4 - График теоретической зависимости холловского сопротивления RH от значения магнитной индукции в образце B

Примечание: при использовании формул (24) и (25)

DOI:10.23670/IRJ.2023.129.38.4

При постоянном значении индукции магнитного поля и переменном напряжении на затворе МОП – транзистора  при использовании формул (22) и (23) диаграмма расположения энергетических уровней будет иметь вид, показанный на рис. 5. Так как , то можно записать соотношение (46):

(46)

где, k – некоторый коэффициент пропорциональности, связывающий величины  и .

Используя соотношение (46), аналогично равенствам (26), (27), (30) на основании диаграммы рис. 5 можно записать следующие соотношения

(47)

Из (47) следует, что .

Используя формулу (36)

и соотношения (47), учитывая, что при использовании формул (22) и (23) числу соответствует полностью заполненный электронами энергетический уровень , числу соответствует полностью заполненный уровень , числу соответствует полностью заполненный уровень и т.д., построим для рассматриваемого случая теоретическую зависимость , которая показана на рис. 6.

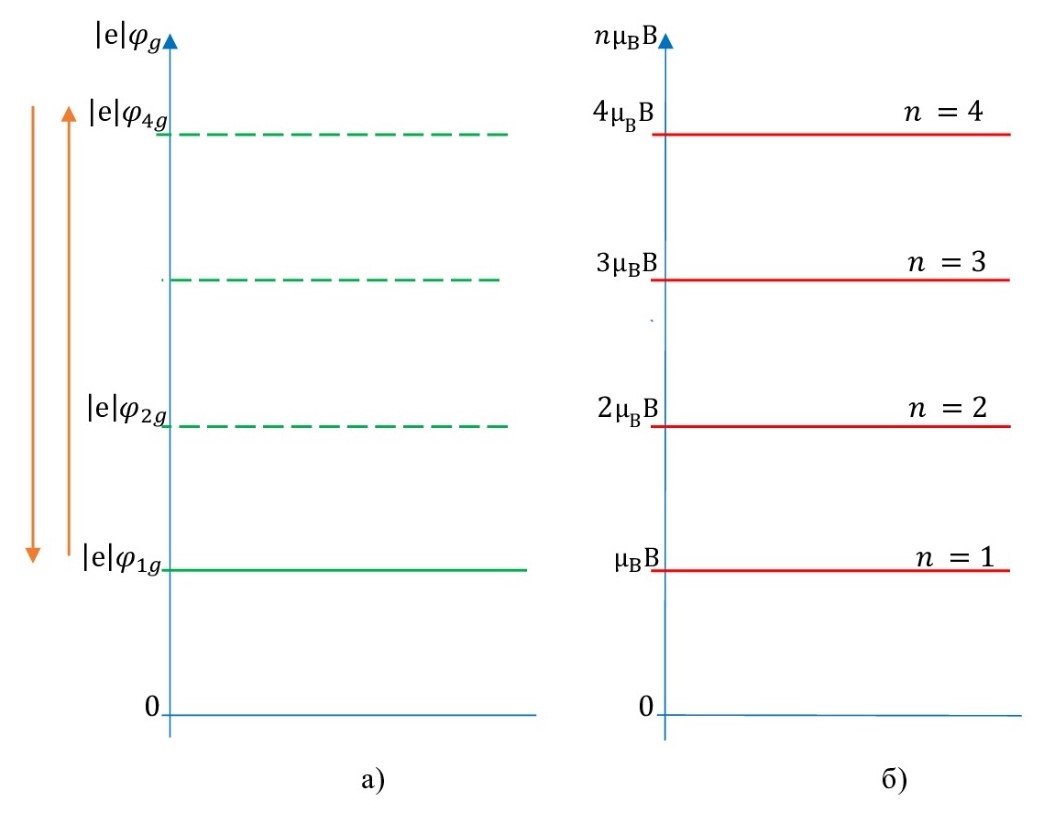
Рисунок 5 - Схематично показана связь между плавным изменением потенциала φg электростатического поля затвора-подложки в зоне проводимости (в 2МЭГ), умноженным на абсолютную величину заряда электрона |e|, и допустимыми значениями энергии электрона в магнитном поле nμBB при B=const:

а - значение потенциала φg электростатического поля затвора-подложки в зоне проводимости, умноженного на абсолютную величину заряда электрона |e|; б - дискретный энергетический спектр системы 2МЭГ в магнитном поле в соответствии с формулами (22) и (23)

Примечание: n - номера дискретных энергетических уровней в 2 МЭГ в соответствии с формулой (22)

DOI:10.23670/IRJ.2023.129.38.5

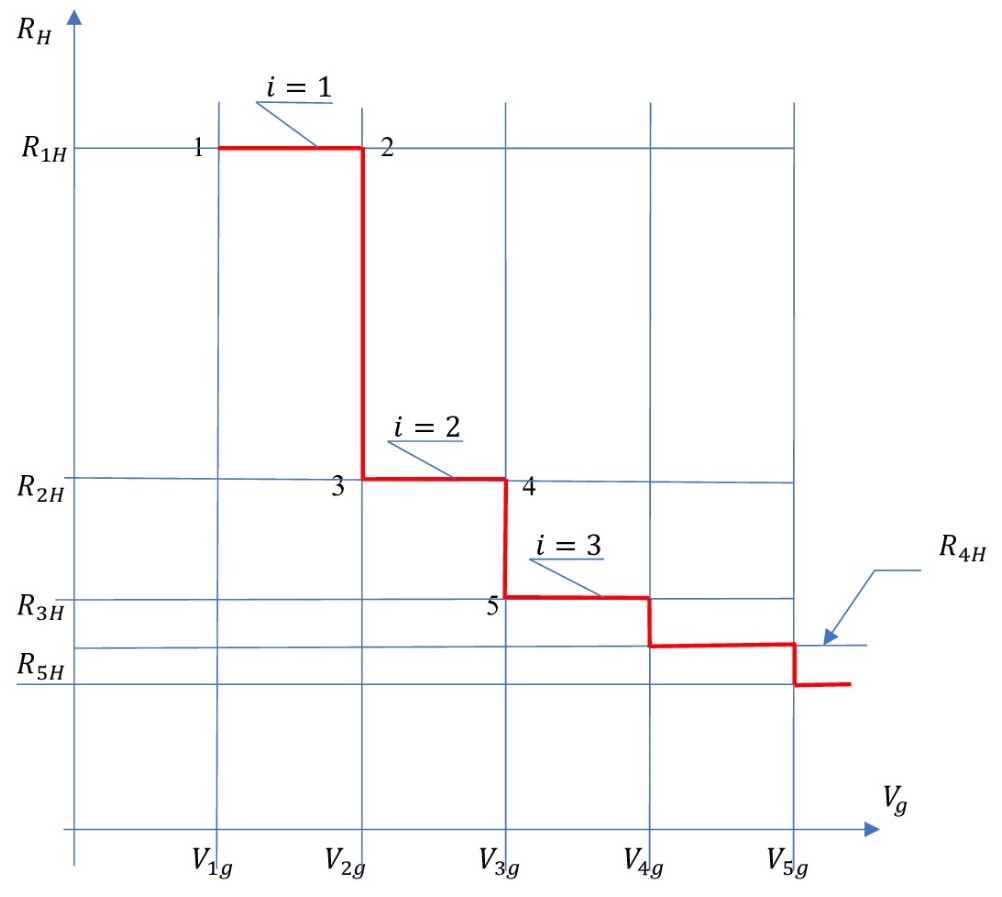
Рисунок 6 - График теоретической зависимости холловского сопротивления RH от напряжения Vg на затворе МОП-структуры транзистора

Примечание: при использовании формул (22) и (23)

DOI:10.23670/IRJ.2023.129.38.6

При использовании формул (24) и (25) диаграмма расположения энергетических уровней будет иметь вид, показанный на рис. 7.

Применяя формулу (46), аналогично соотношениям (47) на основании диаграммы рис. 7 запишем

(48)

Из (48) следует, что . 

Используя формулу (36)

и соотношения (48), учитывая, что при использовании формул (24) и (25) числу соответствует полностью заполненный электронами энергетический уровень , числу соответствует полностью заполненный уровень , числу соответствует полностью заполненный уровень и т.д., построим для рассматриваемого случая теоретическую зависимость , которая показана на рис. 8.

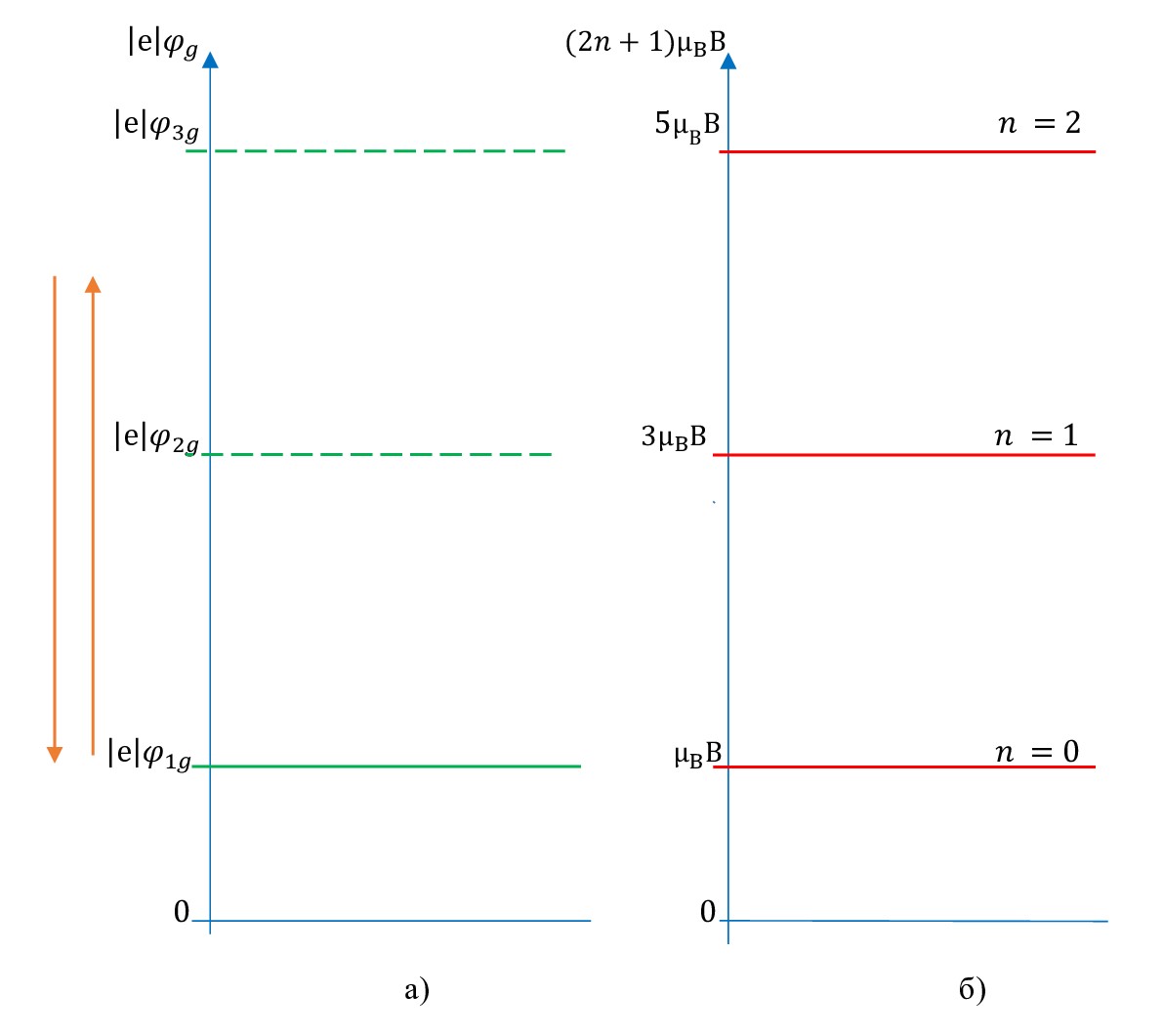
Рисунок 7 - Схематично показана связь между плавным изменением потенциала φg электростатического поля затвора-подложки в зоне проводимости (в 2МЭГ), умноженным на абсолютную величину заряда электрона |e|, и допустимыми значениями энергии электрона в магнитном поле μBB (2n+1) при B=const:

а - значение потенциала φg электростатического поля затвора-подложки в зоне проводимости, умноженного на абсолютную величину заряда электрона |e|; б - дискретный энергетический спектр системы 2МЭГ в магнитном поле в соответствии с формулами (24) и (25)

Примечание: n - номера дискретных энергетических уровней в 2 МЭГ в соответствии с формулой (24)

DOI:10.23670/IRJ.2023.129.38.7

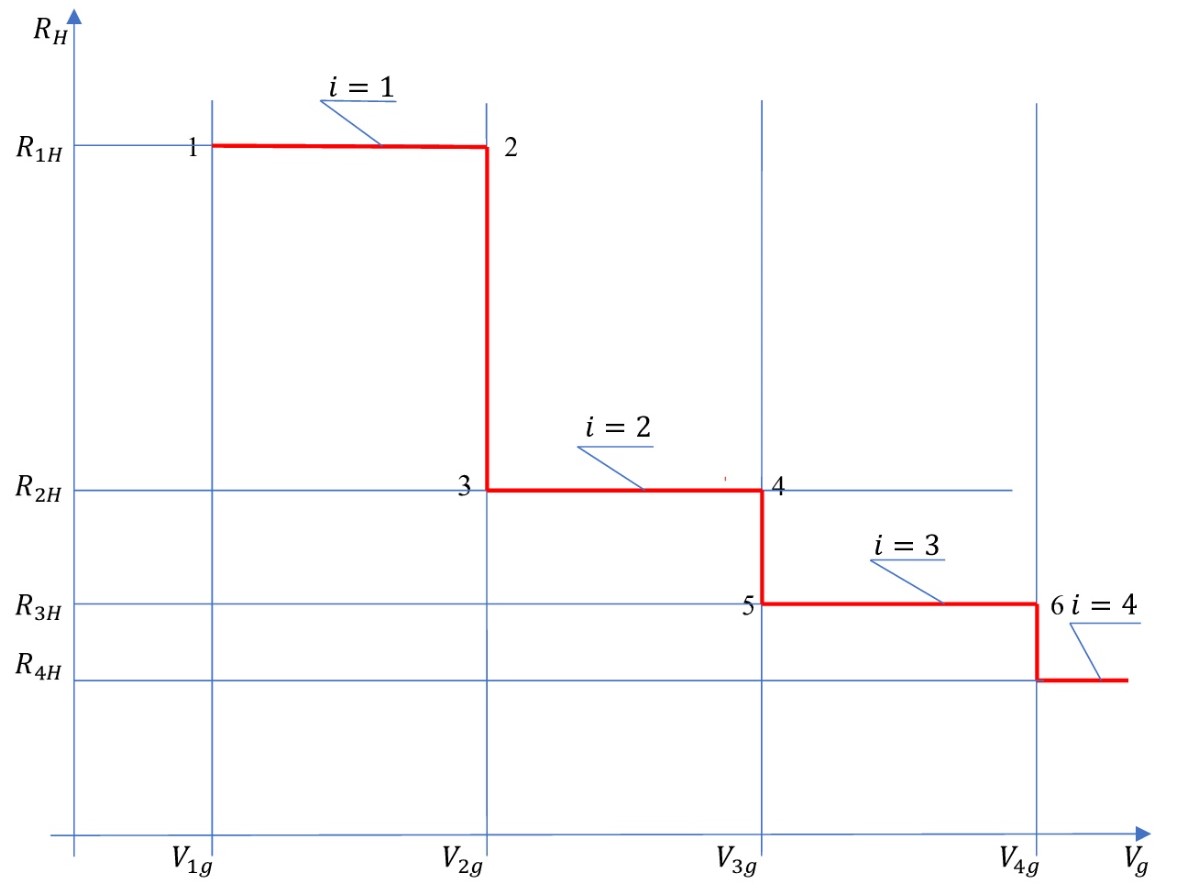
Рисунок 8 - График теоретической зависимости холловского сопротивления RH от напряжения Vg на затворе МОП-структуры транзистора

Примечание: при использовании формул (24) и (25)

DOI:10.23670/IRJ.2023.129.38.8

На рис. 9 показана экспериментальная зависимость холловского сопротивления  и продольного сопротивления от значения индукции магнитного поля, взятая из

[1]

. В данном случае для нас важно наблюдение ЦКЭХ. Плато сопротивления  на рис. 9, соответствующие ЦКЭХ, обозначены цифрами 1, 2, 3, и 4. Значения сопротивлений  вынесены на отдельные линии – полки. На нижнем графике зависимости вертикальными стрелками, обозначенными цифрами 1, 2, 3 и 4, указаны значения индукции , соответствующие целочисленным факторам заполнения . В рассматриваемом случае важно то, что на рис. 9 значения индукции магнитного поля , указанные вертикальными линиями со стрелками и обозначенные как  и  относятся друг к другу с высокой степенью точности в согласии с соотношениями (29), (32) (33) и (34), следующим из формул (22) и (23), то есть . Эти экспериментально наблюдаемые соотношения очевидно противоречат отношениям , следующим из соотношений (40), (43), (44) и (45) и формул (24) и (25). Изменения числа  при значениях индукции  и  в согласии с соотношениями соответствуют и энергетической диаграмме рис.1 и равенствам (26), (27), (30), что свидетельствует о правильности равенств (26), (27), (30) и принципов, положенных в основу построения диаграммы рис. 1.

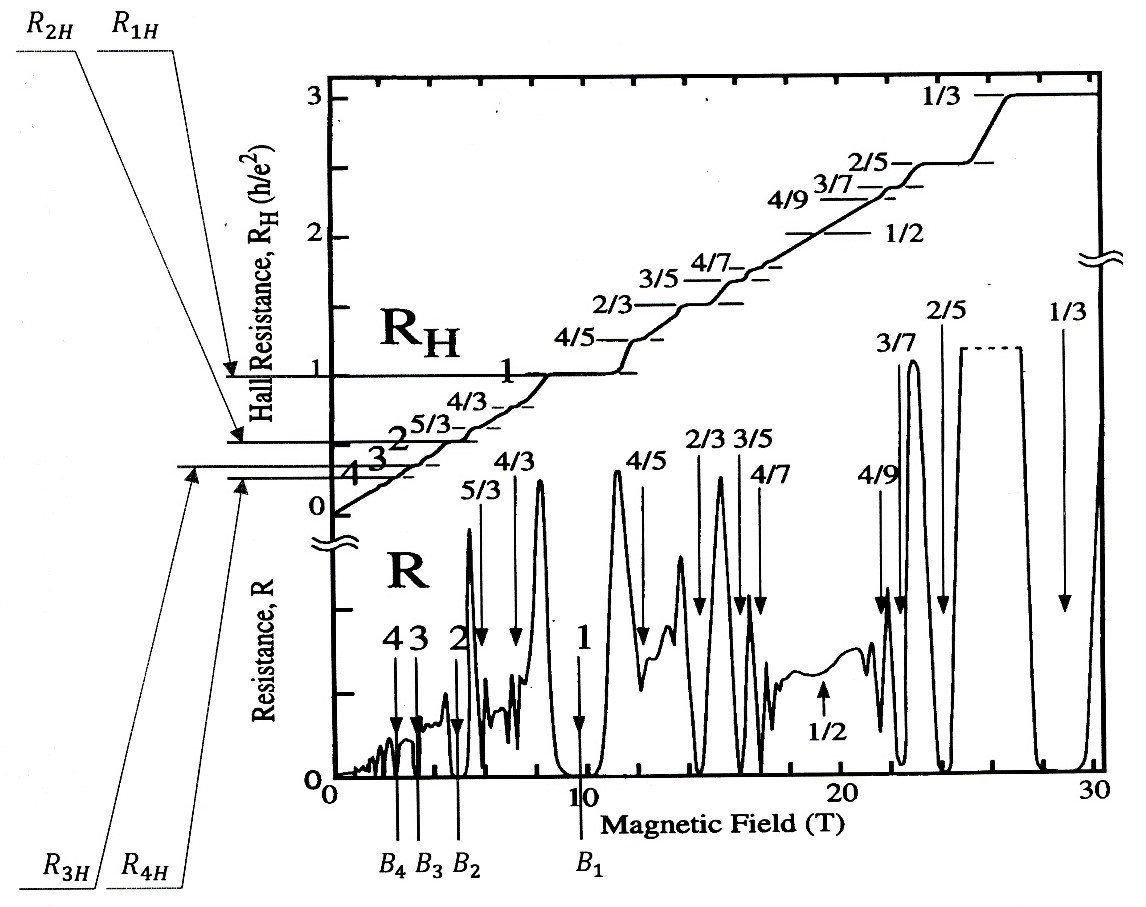
Рисунок 9 - Наблюдение целочисленного и дробного квантового эффекта Холла в гетероструктуре GaAsAlGaAs с высокой подвижностью носителей

Примечание: значения индукции B1, B2, B3, B4 соответствуют целочисленным факторам заполнения i, равным 1, 2, 3, 4

DOI:10.23670/IRJ.2023.129.38.9

Рассмотрим ещё одну экспериментальную зависимость , взятую из

[8]

(см. рис.10), вид которой очень близок к виду аналогичной теоретической зависимости рис.2 в данной статье. На рис.10 отсутствует плато сопротивления . Плато, обозначенное на рис.10 как , не относится к ЦКЭХ, так как отношение к далеко не равно 2, как это должно иметь место при ЦКЭХ. Соответственно на рис.10 не показано и значение индукции . Отношение сопротивления к сопротивлениям и строго соответствует ЦКЭХ. В данном случае на рис. 10 важно то, что отношение значения индукции к индукции с большой точностью равно 1,5, именно такое отношение к следует из формул (29) и (32). Формулы (29) и (32) получены теоретически с использованием диаграммы рис. 1, расположение энергетических уровней на которой соответствует формулам (22) и (23). Согласно формулам (40) и (43), теоретически полученным с использованием диаграммы рис. 3, отношение индукции к индукции должно быть 1,66. Отношение значения индукции к значениям индукции и очень близки к величинам, которые следуют из соотношений (29), (32) (33) и (34) и формул (22) и (23). Таким образом, экспериментальная зависимость рис.10 подтверждает правильность формул (22) и (23) и не согласуется с формулами (24) и (25).

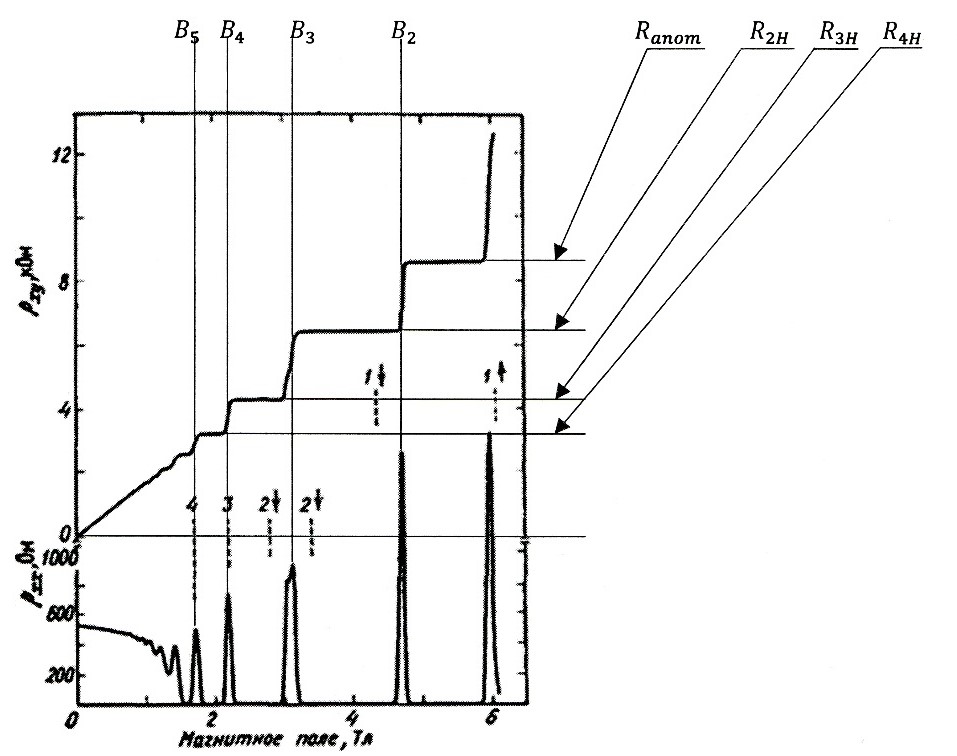
Рисунок 10 - Экспериментальные зависимости холловского сопротивления RH=ρxy и удельного сопротивления ρxx~Rx гетероструктуры от магнитного поля при фиксированной плотности носителей, соответсвтующей напряжению на затворе Vg=0

Примечание: температура около 8 мК

DOI:10.23670/IRJ.2023.129.38.10

Исходя из формул (22) и (23), энергетической диаграммы рис.1, равенств (26), (27), (30), условия (35) можно предсказать не только соотношения между холловскими сопротивлениями  при различных значениях целочисленного фактора заполнения , но можно предсказать также и наличие плато сопротивления  между значениями индукции  и т.д. (см.рис.2). Плато сопротивления  в данном случае появляется как следствие наличия энергетической щели  между энергетическими уровнями в явлении ЦКЭХ, для преодоления энергетической щели необходим некоторый диапазон изменения величин  и  для дискретного заполнения электронами дискретных энергетических уровней в явлении ЦКЭХ. Величина этого диапазона и определяет ширину плато холловского сопротивления. Чётко выраженные плато на рис.10 между значениями индукции  и , при которых происходит изменение числа , подтверждают правильность энергетической диаграммы рис.1 и теоретической зависимости на рис.2.

В связи с предложенным объяснением появления плато холловского сопротивления  нет необходимости в привлечении концепции локализованных и делокализованных электронов. Даже при идеальной однородности потенциала электростатического поля затвора – подложки в 2МЭГ или электростатического поля гетероструктуры, т.е. при отсутствии «гор» и «ям» электростатической энергии электрона в двумерном слое

В случае . и переменного значения напряжения на затворе МОП – транзистора при использовании формул (22) и (23) должны быть справедливы следующие соотношения между значениями напряжения на затворе МОП – транзистора: (см. (47)). При использовании формул (24) и (25) должны быть справедливы соотношения: (см.(48)).

Рассмотрим экспериментальную зависимость , показанную на рис.11, взятом из

Из тех же точек на графике зависимости , из которых выходят горизонтальные тонкие линии, исходят и вертикальные тонкие линии, соответствующие напряжениям на затворе и . Вертикальная шкала не позволяет указать значение сопротивления , соответствующего одному заполненному низшему энергетическому уровню, так же как и горизонтальная шкала B на рис. 10, взятом из

Необходимо отметить, что вид графика хорошо согласуется с теоретической зависимостью рис. 6, что указывает на принципиальную правильность энергетической диаграммы рис. 5 и соотношений (47), лежащих в основе построения зависимости рис.6. Интервалы между величинами и приблизительно равны между собой, при этом величина примерно в 2 раза меньше величины , что согласуется с соотношениями (47), а, следовательно, и с формулами (22) и (23).

Формулы (24) и (25) лежат в основе построения энергетической диаграммы рис.7 и теоретической зависимости рис.8 данной статьи, согласно которым (см. соотношения (48)) значение должно быть в 3 раза больше значения , но такое отношение к не соответствует следующим из графика

Даже не имея точного значения величины , но зная из соотношений (47) и (48), чему должны быть равны отношения друг к другу величин и можно с большой точностью показать, что формулы (22) и (23) соответствуют экспериментальной зависимости

Так, например, согласно формулам (22) и (23) и соотношениям (47) отношение , а согласно формулам (24) и (25) и соотношениям (48) это отношение должно быть равно 2,33. Из экспериментальной зависимости

Следует отметить, что точное определение величин и имеет большое значение для нахождения, предложенным в данной статье методом, величин энергетических уровней, возникающих в магнитном поле в 2МЭГ, поэтому желательно, чтобы будущие исследования ЦКЭХ были направлены на точное определение и .

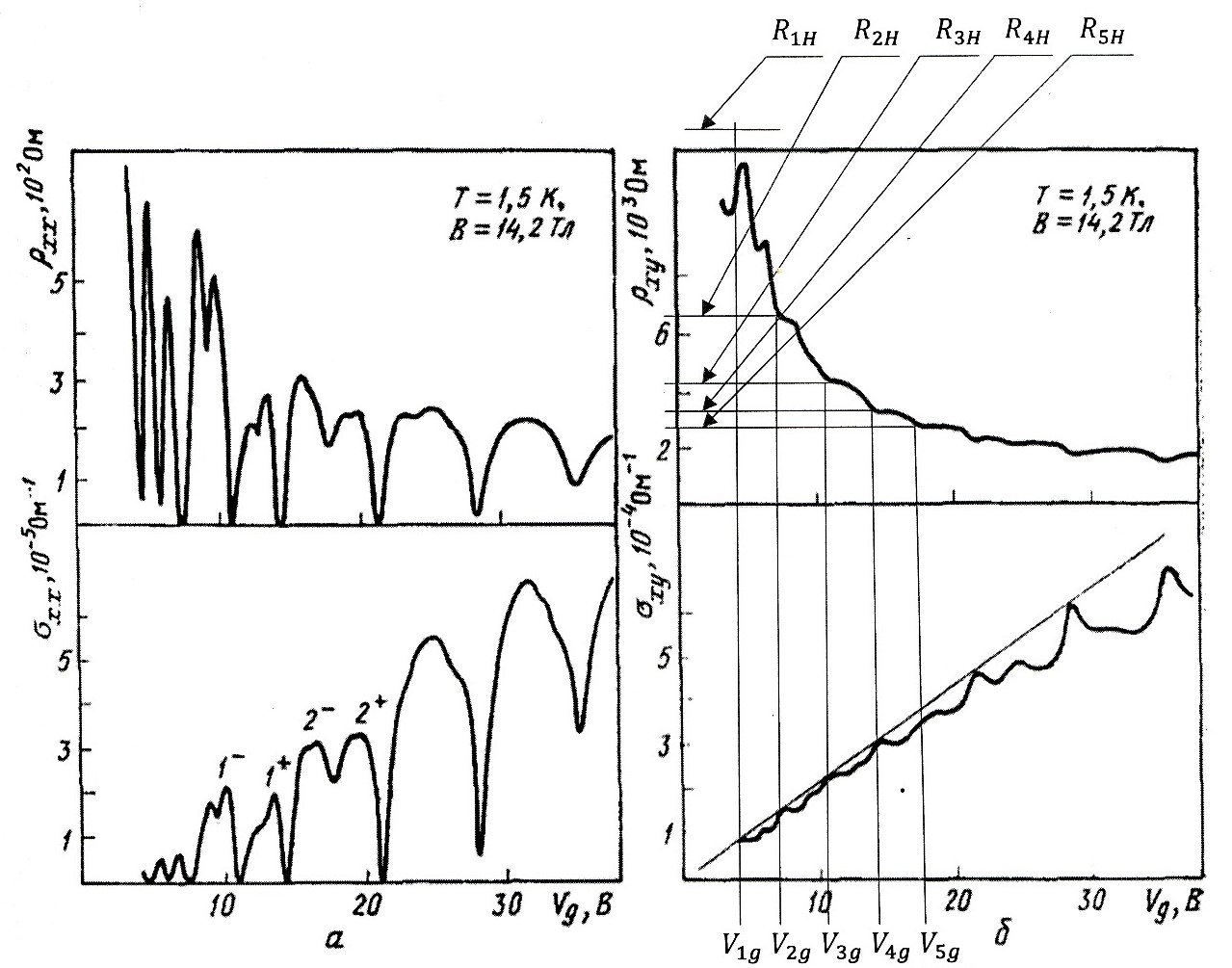
Рисунок 11 - Экспериментальные данные для ρxx и ρxy кремниевого МОП-транзистора вместе с вычисленными значениями σxx и σxy в зависимости от напряжения на затворе при B=14,2 Тл

DOI:10.23670/IRJ.2023.129.38.11

1. Из формулы де Бройля без учёта спиновой степени свободы электрона при значении массы электрона, равной его массе покоя, выведены формулы (11) и (22) для дискретных значений энергии уровня электронов, двигающихся по циклотронным орбитам. Формулы (11) и (22) являются новыми, т.е. полученными впервые и ранее неизвестными. Также являются новыми полученные из формулы (11) формулы (10), (19), (20), (21) и (23).

2. С использованием формулы (11) в разделе 2 данной статьи обоснована справедливость второго постулата Бора (правило квантования орбит) по отношению к движению электронов по циклотронным орбитам в магнитном поле. Обоснование справедливости второго постулата Бора по отношению к движению электронов по циклотронным орбитам в магнитном поле является новым, в современной квантовой физике не рассматривается применение второго постулата Бора в рассматриваемом случае.

3. С использованием формул (22) и (24) для случаев постоянного и переменного значения индукции B построены энергетические диаграммы рис. 1, 3, 5 и 7 для ЦКЭХ при значении массы электрона, равной массе покоя. На основании энергетических диаграмм, показанных на рис. 1, 3, 5 и 7, построены теоретические зависимости и , изображённые на рис. 2, 4, 6 и 8. Как сами теоретические зависимости и , изображённые на рис. 2, 4, 6 и 8, так и метод их построения, основанный на равенствах (26), (27), (30), (37), (38), (41), (47), (48) и условии (35), являются новыми.

4. Дано объяснение появлению плато холловского сопротивления как следствия наличия энергетической щели между энергетическими уровнями в явлении ЦКЭХ. Появление плато в рассматриваемом случае в согласии с равенствами (26), (27), (30), (37), (38), (41), (47), (48) и условием (35) объясняется необходимостью некоторого диапазона изменения величин и для дискретного заполнения электронами дискретных энергетических уровней в явлении ЦКЭХ. Такое объяснение появлению плато холловского сопротивления является новым, при этом нет необходимости использовать концепцию локализованных и делокализованных электронов.

5. Предложен метод измерения энергетических уровней электронов в явлении ЦКЭХ, основанный на теоретических зависимостях и , изображённых на рис. 2, 4, 6 и 8. Этот метод основан на том, что отношения друг к другу величин и в момент дискретного заполнения электронами энергетических уровней должны иметь строго определённые значения. Сравнение указанных отношений с экспериментально измеренными показывает соответствие формул (11), (22) и (23) экспериментальным данным и несогласие с экспериментальными данными формул (1), (24) и (25) при значении массы электрона, равной массе покоя. Предложенный метод измерения энергетических уровней электронов в явлении ЦКЭХ является новым.

В результате проведённого исследования выявлено несоответствие формулы (1) экспериментальным зависимостям холловского сопротивления в функции от значения магнитной индукции и напряжения на затворе МОП – транзистора в явлении ЦКЭХ при значении массы электрона, равной массе покоя. Показано согласие с указанными экспериментальными зависимостями выведенной из формулы де Бройля формулы (22) при значении массы электрона, равной массе покоя.