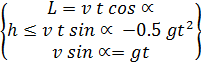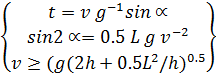CONTROL OF MODEL AND SOLUTION OF PRACTICAL PROBLEMS

Нечитайло А.Н.¹, Погодин И.Е.²

¹ ORCID: 0000-0002-1825-0023, Кандидат химических наук, доцент, ВИ (И-Т) ВА МТО, ² ORCID: 0000-0002-1825-0097, Доктор физико-математических наук, профессор, ВМПИ ВУНЦ ВМФ ВМА, Санкт-Петербург

КОНТРОЛЬ МОДЕЛИ И РЕШЕНИЯ ПРАКТИЧЕСКИХ ЗАДАЧ

Аннотация

Важность адекватности выбираемой модели  и необходимость исследовательского (нешаблонного) подхода к ее решению продемонстрирована на примере  простой задачи.

Ключевые слова: модель, скорость, траектория.

Nechitailo A.N.¹, Pogodin I.E.²

¹ ORCID: 0000-0002-1825-0023, PhD in Chemistry, Associated professor, Military Academy of the Material and Technical Maintenance named by General of the Army A.V. Khrulev, St. Petersburg, ² ORCID: 0000-0002-1825-0097, PhD in Physics and Mathematics, Professor, Naval Polytechnical Institute of N.G. Kuznetsov Naval Academy, St. Petersburg

CONTROL OF MODEL AND SOLUTION OF PRACTICAL PROBLEMS

Abstract

Importance of adequacy to the chosen model and the need of the research (not sample) approach to its decision are shown on the example of a simple problem.

Keywords: model, speed, trajectory.

We will show on the example of a simple problem the importance of research approach to a choice of model and to the search of alternative decisions.

For this purpose it is proposed to consider some various methodically important approaches to the decision of elementary, though rather rare [1] problems of search of the minimal speed allowing in "vacuum" conditions to throw a dot material body through the barrier height of "h" located on horizontal distance of "L" from a position:

1. a) of "an obvious ipromptu",
2. b) of decision of system of inequalities,
3. c) of the physical analysis at the qualitative level.
4. a) Many even skilled professional physicists believes at once that the top of a parabolic trajectory of a body has to appear precisely over the top point of a barrier.

Then, using entered designations of g - for acceleration of gravity, v - for the initial speed forming a corner α with the horizon and t - for flight time to more top point of a barrier:

                                                                      (1)

About that this decision is inadequate to given problem, it is possible to be convinced, for example, considering limit cases: if at  L→0 we receive the true: , but at h→0 is expected v →∞ that is incorrect.

c) Without doing heuristic assumptions of model (a) we start from two kinematic equations in two orthogonal projections:

then we will exclude time t and using parameter:  we will receive a quadratic equation:  =0

We come from the requirement of nonnegativity of its discriminant to the result:

                                                                           (2)

The sign "plus" before the radical is chosen to obtain the correct limit value

 if L→0.

c) Attention is drawn to the simple form (2) of the expression obtained, it is assumed that there may be even more intuitive "semi-quantitative, physical" way to solve. Indeed, in terms of energy problem it is close to the estimation of the required initial velocity of the jumper who is flying to the top of the barrier (coordinates: L, h), uses the pole of the length , and relies the middle point between the points of beginning and end of the flight at an height of 0.5h (real or fictional, chosen length of the pole has no influence on the result). Then its initial kinetic energy has to be equal to the potential energy of the jumper at the top point of trajectory: 0.5m and leads to an expression (2) for minimal necessary speed too.

Interestingly, that from tg (2∝) =-L/h, where ∝   is angle between initial speed vector and horizontal line, flows:    i.e. "aiming" is necessary pithily, located higher than overhead point of barrier on the size of distance from the start point  to the top of barrier. Another feature consists in that the tangent of angle  β of slope of speed of body on the top of barrier with a vertical line is equal i.e. speed of body in the overhead point of barrier is orthogonal to his initial speed at start point.

In summary we will emphasize that the invalidity of the decision (1) of the first model (item "and") was found at research of its consequences (limit transition to small h) and until other solution (2) for comparison was found, it, generally speaking, couldn't be rejected. Points (“b” and "c") showed invariance of result to various methods of its receiving.

So, on the presented example it is shown that at the decision even of simple  physical problem the research approach allows not only to define and expand a scope of the received result, but also to reject decisions which falsehood a priori isn't obvious at all.

References

1. Butikov E.I, Kondratyev A.S. Physics, 2001, M.-SPb., «Physmathlit». - 352 p.