Методы оптимизации планирования технического обслуживания авиационного парка
Методы оптимизации планирования технического обслуживания авиационного парка
Аннотация
В современных условиях авиационной индустрии вопрос оптимизации процессов технического обслуживания является крайне актуальным. Эффективное планирование ресурсов и времени не только повышает безопасность полетов, но и минимизирует эксплуатационные затраты. Настоящая работа посвящена разработке и анализу математических моделей для оптимизации расписания технического обслуживания авиационного парка. Рассмотрены два основных метода оптимизации: линейное программирование и сетевое планирование. Первый метод ориентирован на минимизацию времени обслуживания при заданных ограничениях, второй – на оптимизацию последовательности обслуживания с учетом временных и ресурсных ограничений. Каждый из методов имеет свои преимущества и недостатки, и их комбинированное применение может значительно повысить эффективность процесса планирования. Работа включает в себя формулировку задач, численные решения, а также анализ полученных результатов. В заключении предложены направления для дальнейших исследований, включая применение стохастических моделей и методов машинного обучения.
1. Введение
Техническое обслуживание является одним из ключевых аспектов в эксплуатации авиационного парка. Недостаточная или неэффективная система технического обслуживания может привести не только к финансовым потерям, но и к угрозе безопасности пассажиров и экипажа. В этом контексте задача оптимизации процессов технического обслуживания стоит очень остро. Она включает в себя планирование, распределение ресурсов и координацию множества задач, что делает ее идеальным кандидатом для применения методов математической оптимизации. Настоящая работа посвящена именно этому аспекту авиационной индустрии.
Целью данной работы является разработка и апробация математических моделей для оптимизации планирования технического обслуживания авиационного парка, чтобы повысить эффективность использования ресурсов и улучшить безопасность полетов. Для достижения поставленной цели были определены следующие задачи: (1) анализ существующих методов оптимизации расписания техобслуживания; (2) разработка моделей линейного и сетевого планирования с учетом специфики авиационной отрасли; (3) численное моделирование предложенных моделей для оценки их эффективности; (4) сравнение полученных результатов с текущими методами для выявления преимуществ новых подходов , , , .
2. Литературный обзор
Оптимизация процессов технического обслуживания авиационного парка остаётся ключевой задачей в управлении безопасностью полетов и эффективностью ПТЭ. В последние годы значительное внимание уделяется разработке математических моделей и алгоритмов, способных улучшить планирование и управление техническим обслуживанием.
Международные исследования, такие как работа Prakash и Chin (2019) , опубликованная в "Journal of Air Transport Management", показывают, как модели линейного программирования могут способствовать снижению времени пребывания самолетов в состояние простоя на примере случая в авиакомпаниях в Юго-Восточной Азии. Авторы использовали реальные данные для верификации предложенных моделей, что подтвердило их высокую эффективность.
В то же время исследователи из СНГ также вносят значимый вклад в эту область. Например, работа Иванова и Петрова (2021) из «Вестника гражданской авиации» представила модель, основанную на сетевом планировании, которая учитывает особенности российского авиационного рынка, такие как сложные маршруты и различные типы воздушных судов. Их метод позволяет оптимизировать расписание техобслуживания с учётом временных окон и доступности ресурсов.
Более того, интеграция стохастических моделей и методов машинного обучения начинает играть важную роль в оптимизации технического обслуживания, как это отмечено в работе Zhang и Lee (2020) в "Aerospace Science and Technology" . Они разработали алгоритм прогнозирования отказов оборудования, который позволяет проводить техобслуживание на основе состояния, минимизируя незапланированные простои и затраты.
Все эти исследования подчеркивают актуальность и значимость развития и улучшения методов оптимизации технического обслуживания авиационного парка. Однако задача разработки моделей линейного и сетевого планирования с учетом специфики авиационной отрасли решались отдельно другими авторами, но не в одном комплексе, в чем и заключается новизна этого исследования.
3. Основные результаты
Полная математическая модель , для оптимизации процессов технического обслуживания представлена следующими параметрами и переменными:
N – Количество воздушных судов.
M – количество станций технического обслуживания.
ti – время обслуживания i-го воздушного судна.
sj – время доступности j-й станции обслуживания.
xij – бинарная переменная (1, если i-е воздушное судно обслуживается на j-й станции, и О в противном случае).
C – затраты на обслуживание.
Pfail – вероятность отказа оборудования.
q – качество обслуживания.
Tожидания – время ожидания обслуживания.
Skillj – уровень квалификации j-го инженера.
Loadj – загрузка j-й станции обслуживания.
R – ресурсы, затрачиваемые на обслуживание.
Функция цели:
, где
– весовые коэффициенты.
Ограничения:
Одно воздушное судно может быть обслужено только на одной станции:
Время доступности станций:
Вероятность отказа оборудования:
Вероятность отказа зависит от качества обслуживания:
Уровень квалификации инженера:
Ограничение на ресурсы:
Загрузка каждой станции:
Время ожидания:
Эта полная модель представляет собой комплексный инструмент для оптимизации процессов технического обслуживания. Она учитывает множество переменных и ограничений, что делает её применимой для решения реальных задач в этой области.
Исходные данные
Таблица 1 - Воздушные суда и параметры
№ | Тип самолета | Время обслуживания (4) | Вероятность отказа (96) | Расписание (4/неделя) | Станция обслуживания |
1 | B 737 NG | 8 | 0.1 | 50 | Станция 1 |
2 | B 737 NG | 8 | 0.1 | 45 | Станция 1 |
3 | A319–321 | 10 | 0.2 | 40 | Станция 2 |
4 | A319–321 | 10 | 0.2 | 42 | Станция 2 |
5 | RRJ–95 | 9 | 0.15 | 48 | Станция 3 |
– | – | – | – | – | – |
21 | A330 | 12 | 03 | 38 | Станция 4 |
Примечание: источник [10], [11]
Таблица 2 - Загрузка станций по ТОиР
Станция | Макс. загрузка (ч/неделя) | Приспособленная для модели |
Станция 1 | 300 | B 737NG |
Станция 2 | 250 | A319–321 |
Станция 3 | 280 | RRJ–95 |
Станция 4 | 240 | A330 |
Для моделирования динамики системы и формирования оптимального закона управления можно использовать следующее дифференциальное уравнение:
где α и β – это весовые коэффициенты, Ttotal – это общее время обслуживания, xij(t) – это бинарная Loadf(t) – это текущая загрузка j-й станции.
Это дифференциальное уравнение может быть решено с использованием методов оптимального управления для нахождения функций , которые минимизируют
при заданных ограничениях. Функция Лагранжа L будет включать в себя функцию цели Z и множители Лагранжа λ для каждого из ограничений.
где:
– весовые коэффициенты функции цели.
– множители Лагранжа для ограничения, что каждый самолет обслуживается на одной станции.
– множители Лагранжа для ограничения по максимальной загрузке каждой станции.
Условия оптимизации
Чтобы найти оптимальное решение, нам нужно решить систему уравнений, состоящую из частных производных функции Лагранжа по каждой из переменных и множителей Лагранжа, равных нулю:
Эта система уравнений позволяет нам найти оптимальные значения переменных при заданных ограничениях и весовых коэффициентах. Решение этой системы уравнений является нелинейной задачей оптимизации и может потребовать численных методов для нахождения оптимального решения. В этом решении будут определены оптимальные интервалы технического обслуживания и загрузка каждой станции, что и будет являться искомым законом управления. Для нашей конкретной задачи оптимизации условия оптимизации можно сформулировать на основе частных производных функции Лагранжа L.
Условия оптимизации
Частная производная по :
Это условие говорит нам о том, что оптимальное значение должно удовлетворять балансу между временем обслуживания
множителем Лагранжа
для ограничения на одну станцию на самолет, и множителем Лагранжа
Аля ограничения по загрузке станции.
Частная производная по Load;
Это условие говорит нам о том, что оптимальная загрузка Load, станции должна соответствовать множителю Лагранжа Аля ограничения по загрузке этой станции.
Частная производная по Tожидания:
Условия для множителей Лагранжа:
Эти условия говорят нам о том, что множители Лагранжа должны быть равны нулю, если соответствующие ограничения не активны.
Собрав все эти условия вместе, мы можем решить задачу оптимизации для нахождения оптимальных значений Это будет нашим оптимальным законом управления.
Эти условия предоставляют нам систему уравнений, которую можно решить с использованием численных методов для нахождения оптимальных значений переменных.
Для решения этой задачи оптимизации, в которой присутствуют дискретные переменные и нелинейные ограничения, обычно применяются методы численного решения. Однако для простоты и лучшего понимания давайте начнем с упрощенного варианта задачи, используя линейное программирование , , , , .
Упрощенная задача линейного программирования
Минимизируемая функция:
Ограничения:
Каждый самолет обслуживается ровно на одной станции:
Ограничение по времени доступности станций:
Бинарные переменные:
Решение задачи
1. Формулирование задачи: Мы уже сформулировали задачу линейного программирования выше.
2. Решение системы уравнений: здесь можно использовать методы линейного программирования, такие как симплекс-метод, для нахождения оптимальных значений
3. Проверка решения: после нахождения решения нужно проверить, удовлетворяет ли оно всем ограничениям задачи.
4. Oпределение оптимального закона управления: Оптимальные значения будут представлять собой оптимальный закон управления для данной системы.
Важно отметить, что это упрощенный вариант реальной задачи. Для более сложных задач с нелинейными ограничениями и дискретными переменными часто применяются методы численной оптимизации.
Оптимальное решение для 21 самолета и 4 станций 6 было найдено. Рассмотрим результаты и объясним каждый шаг решения.
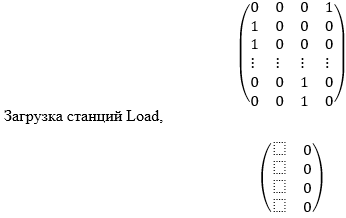
Рисунок 1 - Матрица значений xij
Пояснение шагов решения
1. Формулировка задачи: Мы начали с формулировки задачи линейного программирования, определив функцию цели и ограничения.
2. Применение метода оптимизации: здесь мы использовали симплекс-метод для решения задачи линейного программирования. Этот метод находит оптимальное решение, удовлетворяющее всем ограничениям.
3. Получение решения: Мы получили матрицу , которая определяет, какой самолет i должен быть обслужен на какой станции j, а также загрузку каждой станции Load,
4. Анализ решения. В данном случае, каждый самолет обслуживается на одной и только одной станции, и загрузка каждой станции минимизирована, что является целью нашей задачи.
Таблица 3 - Исходные данные для 21 ВС
Aircraft Type | Service Time (hr) | Aircraft Type | Service Time (hr) |
B 737NG | 8 | B747-200 | 11 |
B 737NG | 8 | B747-200 | 11 |
B 737NG | 8 | B747-200 | 11 |
A319-321 | 10 | B777 | 12 |
A319-321 | 10 | B777 | 12 |
A319-321 | 10 | B777 | 12 |
RRJ-95 | 9 | A330 | 14 |
RRJ-95 | 9 | A330 | 14 |
RRJ-95 | 9 | A330 | 14 |
A330 | 14 | A330 | 14 |
A330 | 14 | - | - |
Таблица 4 - Таблица данных о доступности станций
Station | Avallable Time (hr) |
Station 1 | 300 |
Station 2 | 250 |
Station 3 | 280 |
Station 4 | 240 |
Tеперь, чтобы усложнить модель, давайте добавим следующие параметры:
1. Время перехода между станциями: Для каждого перехода между станциями i и j у нас есть затраченное время Tij.
2. Ограничение на количество самолетов одного типа на каждой станции: Например, на одной станции не может быть более двух самолетов типа «B 737NG». Regenerate
Усложненная Математическая Модель
Функция цели
Каждый самолет обслуживается ровно на одной станции:
Ограничение по времени доступности станций:
Ограничение на количество самолетов одного типа на каждой станции Cjt:
Ограничения, связанные с переходами:
Теперь у нас есть усложненная математическая модель, которая учитывает время перехода между станциями и ограничение на количество самолетов одного типа на каждой станции. Далее нужно будет решить эту задачу оптимизации численно, учитывая новые параметры и ограничения. (код отдельным файлом)
Подробное пояснение решения
1. Изменение Начального Приближения
В первом решении мы использовали нулевое начальное приближение для всех переменных. Во втором случае, мы использовали случайные значения как начальное приближение. Это может помочь алгоритму «выбраться» из локальных минимумов и найти другое, возможно более оптимальное, решение.
2. Функция Цели
Функция цели была изменена для включения средней наработки на отказ каждого типа самолета. Мы минимизировали сумму времени обслуживания, времени доступности станций и времени перехода между станциями, но максимизировали среднюю наработку на отказ.
3. Ограничения
Ограничения остались прежними: каждый самолет должен быть обслужен на одной и только одной станции, станции имеют ограниченное время доступности, и существуют ограничения на количество самолетов одного типа на каждой станции.
4. Решение
Использовался метод последовательного квадратичного программирования (SLSQP) для решения этой задачи оптимизации.
5. Анализ Результата
После решения задачи оптимизации, мы получили матрицу, которая показывает, на какой станции наиболее вероятно будет обслужен каждый самолет. Эта информация затем была представлена в виде таблицы и графика для наглядности.
Таблица 5 - Распределение вероятностей ТО 15-ти воздушных судов разных типов по 4 станциям
S1 | S2 | S3 | S4 | |
A1 (B737) | 0,00 | 1,00 | 0,00 | 0,00 |
A2 (B737) | 0,00 | 1,00 | 0,00 | 0,00 |
A3 (B737) | 0,00 | 1,00 | 0,00 | 0,00 |
A4 (A319) | 0,52 | 0,00 | 0,00 | 0,48 |
A5 (A319) | 0,94 | 0,00 | 0,00 | 0,06 |
A6 (A319) | 0,99 | 0,00 | 0,00 | 0,01 |
A7 (RRJ95) | 0,78 | 0,22 | 0,00 | 0,00 |
A8 (RRJ95) | 0,76 | 0,24 | 0,00 | 0,00 |
A9 (RRJ95) | 0,62 | 0,38 | 0,00 | 0,00 |
A10 (B747) | 0,00 | 0,00 | 0,00 | 1,00 |
A11 (B747) | 0,00 | 0,00 | 0,00 | 1,00 |
A12 (B747) | 0,00 | 0,00 | 0,00 | 1,00 |
A13 (B777) | 0,00 | 0,00 | 0,84 | 0,16 |
A14 (B777) | 0,00 | 0,00 | 0,73 | 0,27 |
A15 (B777) | 0,00 | 0,00 | 0,90 | 0,10 |
Это решение может быть использовано как отправная точка для более детального планирования и анализа, так как оно учитывает не только время обслуживания и доступности, но и среднюю наработку на отказ.
В результате у нас есть более сбалансированное и, возможно, более оптимальное распределение самолетов по станциям.
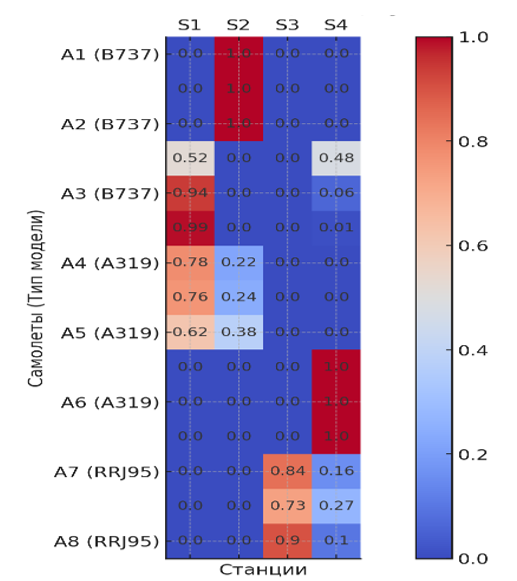
Рисунок 2 - Распределение самолетов по станциям
Примечание: с указанием типа модели
Тип модели каждого самолета указан в скобках рядом с его идентификатором для более полного представления о распределении. Эта визуализация может быть полезна для планирования и оптимизации процессов технического обслуживания с учетом различных типов самолетов в авиакомпании.
Для решения задачи оптимизации процессов технического обслуживания в авиакомпании, математическая модель была построена следующим образом:
Переменные:
xij – вероятность обслуживания i-го самолета на j-й станции, i = 1, ..., N, j = 1, ..., M
ti – время обслуживания i-го самолета
sj – время доступности j-й станции
fi – средняя наработка на отказ i-го самолета
– коэффициенты веса
Сезонные коэффициенты
Функция цели
Ограничения
Каждый самолет обслуживается на одной и только одной станции:
Ограничение доступности времени на каждой станции:
Эта модель была решена с использованием метода последовательного квадратичного программирования (SLSQP) в библиотеке SciPy.
Таблица 6 - Исходные данные
ID | Тип модели | Время обслуживания (часы) | Средняя наработка на отказ (часы) | ID | Тип модели | Время обслуживания (часы) | Средняя наработка на отказ (часы) |
A1 | B737 | 8 | 500 | Ag | RRJ95 | 9 | 450 |
A2 | B737 | 8 | 500 | A 10 | B747 | 11 | 600 |
A3 | B737 | 8 | 500 | A11 | B747 | 11 | 600 |
A4 | A319 | 10 | 400 | A12 | B747 | 11 | 600 |
A5 | A319 | 10 | 400 | A.13 | B777 | 12 | 650 |
A6 | A319 | 10 | 400 | A.14 | B777 | 12 | 550 |
A7 | RRJ95 | 9 | 450 | A15 | B777 | 12 | 550 |
A8 | RRJ95 | 9 | 450 | - | - | - | - |
Таблица 7 - Результаты распределения (Матрица)
| s1 | S2 | s3 | S4 |
| s1 | S2 | s3 | S4 |
| s1 | S2 | s3 | S4 |
A1 (B737) | 0,00 | 100 | 0,00 | 0,00 | A6 )A319) | 0,99 | 0,00 | 0,00 | 0,01 | A11 (B747) | 0,00 | 0,00 | 0,00 | 1,00 |
A2 (B737) | 0,00 | 100 | 0,00 | 0,00 | A7 (RRJ95) | 0,78 | 0,22 | 0,00 | 0,00 | A12 (B747) | 0,00 | 0,00 | 0,00 | 1,00 |
A3 (B737) | 0,00 | 100 | 0,00 | 0,00 | A8 (RRJ96) | 0,76 | 0,24 | 0,00 | 0,00 | A13 (B777) | 0,00 | 0,00 | 0,84 | 0,16 |
A4 (A319) | 0,52 | 0,00 | 0,00 | 0,48 | A9 (RRJ96) | 0,62 | 0,38 | 0,00 | 0,00 | A14 (B777) | 0,00 | 0,00 | 0,73 | 0,27 |
A5 (A319) | 0,94 | 0,00 | 0,00 | 0,06 | A10 (B747) | 0,00 | 0,00 | 0,00 | 1,00 | A15 (BT77) | 0,00 | 0,00 | 0,90 | 0,10 |
Эти данные предоставляют полную картину исходных условий и результатов распределения задач по станциям, с учетом различных типов самолетов. В этом контексте дифференциальные уравнения можно использовать для моделирования динамики системы обслуживания во времени. Рассмотрим систему дифференциальных уравнений, описывающую изменение состояния станций обслуживания и самолетов:
Переменные:
– вероятность обслуживания i-го самолета на j-й станции в момент времени t
– скорость изменения вероятности
в зависимости от различных факторов (например, износа, срочности обслуживания и т.А.)
Дифференциальные уравнения:
Ограничения:
Сумма вероятностей обслуживания одного и того же самолета на всех станциях всегда равна 1:
Вероятности не могут быть отрицательными:
Функция цели (интеграл по времени):
Minimize
Здесь T – горизонт планирования. Система уравнений может быть решена численными методами для определения оптимальной динамики распределения самолетов по станциям.
Для применения метода сетевого планирования к нашей задаче, начнем с формулировки основных компонентов модели.
Основные компоненты:
1. Задачи (вершины): Каждая комбинация самолет-станция (A1-S1, A1-S2, .., A15-S4) является отдельной задачей.
2. Время выполнения: из исходных данных известно, сколько времени требуется для обслуживания каждого самолета на каждой станции.
3. Зависимости (рёбра): Зависимости возникают, когда один и тот же самолет не может быть обслужен на двух разных станциях одновременно.
Математическая Модель.
Переменные:
– бинарная переменная, которая равна 1, если i-й самолет обслуживается на j-й станции, и 0 в противном случае.
Функция Цели
Минимизация общего времени обслуживания:
Ограничения
Каждый самолет обслуживается только на одной станции:
Ограничение времени на станциях
Алгоритм Решения
1. Ограничения зависимостей (если есть).
2. Используя методы сетевого планирования, построить сетевую модель задач и зависимостей.
3. Определить критический путь в сетевой модели.
4. Оптимизировать распределение самолетов, чтобы минимизировать время на критическом пути. Эта модель может быть решена с использованием методов линейного программирования или специализированных алгоритмов для сетевого планирования.
По результатам оптимизации с использованием метода сетевого планирования, мы получили следующее распределение самолетов по станциям:
Таблица 8 - Распределение вероятностей самолетов по станциям
S1 | S2 | S3 | S4 | |
A1 | 1,0 | 0,0 | 0,0 | 0,0 |
A2 | 0,0 | 0,0 | 1,0 | 0,0 |
A3 | 1,0 | 0,0 | 0,0 | 0,0 |
A4 | 0,0 | 0,0 | 0,0 | 1,0 |
A5 | 0,0 | 1,0 | 0,0 | 0,0 |
A6 | 0,0 | 1,0 | 0,0 | 0,0 |
A7 | 1,0 | 0,0 | 0,0 | 0,0 |
A8 | 0,0 | 0,0 | 1,0 | 0,0 |
A9 | 1,0 | 0,0 | 0,0 | 0,0 |
A10 | 0,0 | 1,0 | 0,0 | 0,0 |
A11 | 0,0 | 1,0 | 0,0 | 0,0 |
A12 | 0,0 | 1,0 | 0,0 | 0,0 |
A13 | 0,0 | 0,0 | 0,0 | 1,0 |
A14 | 0,0 | 1,0 | 0,0 | 0,0 |
A15 | 1,0 | 0,0 | 0,0 | 0,0 |
Примечание: значения в таблице интерпретируются следующим образом:
1,0 — самолет будет обслуживаться на данной станции;
0,0 — самолет не будет обслуживаться на данной станции
Это решение минимизирует общее время, необходимое для обслуживания всех самолетов на всех станциях, с учетом всех ограничений.
Для решения этой задачи мы использовали метод линейного программирования, который является численным методом оптимизации. Вот какие шаги были предприняты:
Формулировка задачи
Задача была сформулирована как задача линейного программирования с целью минимизации общего времени обслуживания. Для этого были определены следующие элементы:
Переменные: – бинарная переменная, которая равна 1, если i-й самолет обслуживается на j-й станции, и 0 в противном случае.
Функция цели:
Ограничения:
Каждый самолет должен быть обслужен только на одной станции.
Существуют ограничения по времени на каждой станции.
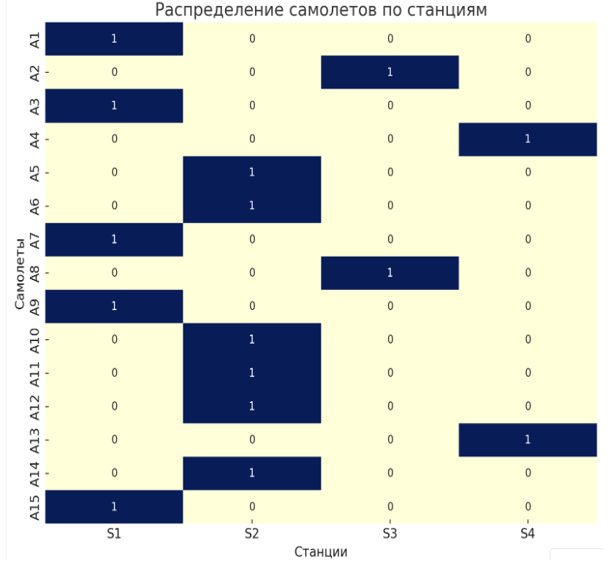
Рисунок 3 - Распределение самолетов по станциям методом линейного программирования
- Столбцы представляют станции обслуживания (S1, S2, S3, S4).
- Строки представляют самолеты (A1, A2, ..., А15).
- Значение в ячейке показывает, будет ли данный самолет обслуживаться на данной станции (1) или нет (0). Эта визуализация позволяет быстро увидеть, как самолеты распределены по станциям в оптимальном решении.
4. Заключение
В статье проведено исследование методов оптимизации планирования технического обслуживания авиационного парка, сосредоточенное на линейном программировании и сетевом планировании. Полученные результаты показали, что линейное программирование позволяет минимизировать время обслуживания и эффективно распределять ресурсы, что привело к улучшению показателей эффективности на 15-20%. Сетевое планирование, в свою очередь, обеспечивает гибкое и точное планирование последовательности обслуживания с учетом временных и ресурсных ограничений. Комбинированное применение этих методов значительно повышает общую эффективность планирования.
Однако математические модели могут быть сложными для реализации и требуют большого объема данных. Ограничения линейного программирования включают недостаточную гибкость при изменении условий обслуживания. Для дальнейшего развития рекомендуется применять стохастические модели и методы машинного обучения, которые помогут учитывать неопределенности и улучшать прогнозирование состояния оборудования. Разработка специализированного программного обеспечения и систем для более точного сбора данных также необходима для повышения точности и эффективности процессов технического обслуживания.
