МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ ПРИМЕНЕНИЯ ЛОГИКО-ВЕРОЯТНОСТНОСТНОГО МЕТОДА В ПЕДАГОГИЧЕСКИХ ИССЛЕДОВАНИЯХ
МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ ПРИМЕНЕНИЯ ЛОГИКО-ВЕРОЯТНОСТНОСТНОГО МЕТОДА В ПЕДАГОГИЧЕСКИХ ИССЛЕДОВАНИЯХ
Аннотация
В современных условиях возрастает потребность в различных подходах к анализу сложных динамических педагогических систем. В работе подчёркнута принципиальная применимость логико-вероятностного метода для анализа педагогической системы. Акцентировано различие в данных и их интерпретациях для технической и педагогической систем. Описаны процедуры адаптации метода с учётом специфики образовательных объектов. Приведён пример использования логико-вероятностного метода для оценки риска неуспеваемости студента первого курса по одному из ключевых предметов основного блока учебного плана. Сделан акцент на расширении возможностей ряда методов при совместном использовании с логико-вероятностным методом.
1. Введение
Логико-вероятностный метод (ЛВМ) сочетает в себе инструменты булевой алгебры (математическая логика) и теории вероятностей, и применяется с целью получения количественной оценки вероятности наступления системного события (успех/неудача) на основе анализа сценариев и принятия обоснованных решений. Задача ЛВМ — найти вероятность того, что логическая функция, описывающая состояние системы, примет определённое значение (например, вероятность отказа), зная вероятности исходных данных (случайные события). На рисунке 1 в виде схемы приведён алгоритм работы ЛВМ. Традиционно ЛВМ активно используется для оценки надёжности сложных технических систем (ТС), но его высокая степень абстракции позволяет провести его содержательную трансформацию к другим областям , , , .
Педагогическая система (ПС) представляет собой сложную, многофункциональную систему, где есть свои «отказы» (неудачи) и «успешные сценарии», чётко определённые цели, множество влияющих внешних факторов, поэтому ЛВМ можно рассматривать как один из инструментов, для описания сложности и неопределённости образовательных процессов.
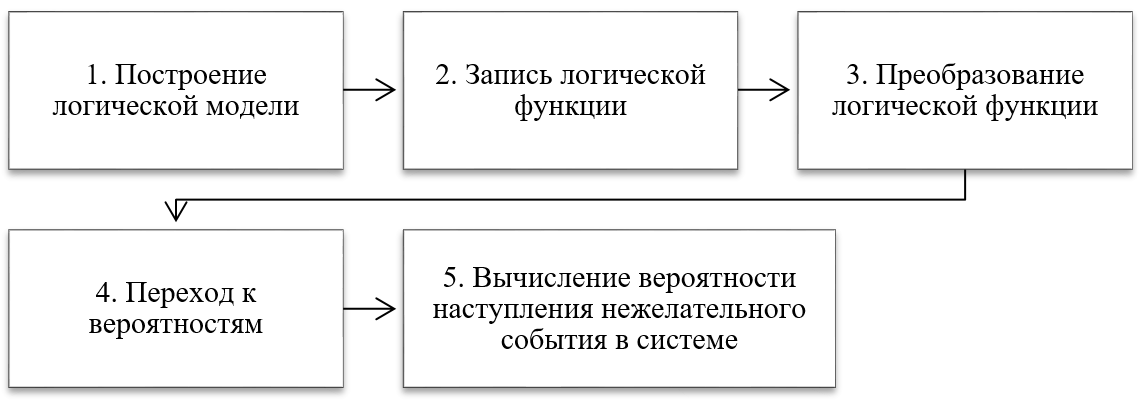
Рисунок 1 - Алгоритм применения ЛВМ
2. Основные результаты
Во время исследования для обоснования возможности применения логико-вероятностного метода к педагогической системе мы провели аналогии между техническими и педагогическими системами (табл. 1). Основная сложность при использовании логико-вероятностного метода для анализа педагогической системы — переход от объективных технических показателей к субъективным педагогическим факторам. Гибкость логико-вероятностного метода позволяет провести системную методологическую адаптацию при сохранении строгости, содержательной адекватности при работе с объектами педагогической системы: жёсткие причинно-следственные связи технических систем замещаются вероятностными оценками, логические операторы описывают не детерминированные условия, а сценарии возможного исхода (вероятности базовых событий технических систем опираются на статистику отказов, в педагогике — на экспертные оценки, данные образовательной статистики).
Таблица 1 - Аналогии между технической и педагогической системами
Техническая система | Педагогическая система |
Отказ системы (авария) | Риск недостижения педагогической цели (низкая успеваемость, эмоциональное выгорание и др.) |
Базовые «рисковые» события — отказы компонентов (отказ элемента, разрыв трубы и др.) | Базовые «рисковые» события — совокупность психолого-педагогических и организационных факторов риска недостижения педагогической цели (низкая мотивация, пробелы в знаниях и др.) |
Логические связки (и, или) | Условия, при которых педагогическая цель недостигнута (конфликт с преподавателем, конфликт в группе, некачественные учебные материалы и др.) |
Нормативно-подушевое финансирование вузов и сохранение контингента студентов — две стороны одной медали современного образования. На основе логико-вероятностного метода мы оценили риск неуспеваемости студента первого курса, обучающегося по специальности «Математика и информатика» в ЛГПУ им. П.П. Семенова-Тян-Шанского, по одному из ключевых предметов — «Алгебра»:
1. Определение нежелательного события (верхушка дерева сценариев) – Y= «Студент не освоил предмет к концу семестра» (набрал < 40 баллов за работу в семестре).
2. Основываясь на практическом опыте, выделение базового события (факторы риска):
‒ X1 = «Студент имеет пробелы в базовых знаниях»;
‒ X2 = «Студент имеет низкую учебную мотивацию»;
‒ X3 = «Недостаточный уровень методологического обеспечения учебного процесса»;
‒ X4 = «Предполагается значительный объем самостоятельной работы, способствующей формированию компетенции»;
‒ X5 = «Высокая учебная нагрузка и ограниченные временные рамки»;
‒ X6 = «Отсутствие поддержки со стороны куратора/одногруппников».
3. На основании экспертного метода (мнения квалифицированных специалистов – педагогов (5 человек)) построение «дерево неудачи», т.е. определение логических связей с использованием логических операций.
Эксперты считают, что студент попадёт в список неуспевающих, если:
‒ студент имеет пробелы в базовых знаниях (И) низкую учебную мотивацию к предмету (И) недостаточный уровень методологического обеспечения учебного процесса;
(ИЛИ)
‒ студент имеет пробелы в базовых знаниях (И) низкую учебную мотивацию к предмету (И) предполагается значительный объем самостоятельной работы, способствующей формированию компетенций;
(ИЛИ)
‒ высокая учебная нагрузка и ограниченные временные рамки (И) отсутствие поддержки со стороны куратора / одногруппников.
С учётом выделенных базовых событий логическая функция в форме ДНФ (дизъюнктивная нормальная форма), описывающая риск неуспеваемости студента первого курса, имеет вид:
Y(X1,X2,X3,X4,X5,X6)= (X1 X2 X3) (X1 X2 X4) (X5 X6).
4. На основании системы методов, таких как анкетирование, статистические данные (результаты контрольных мероприятий, диагностики), экспертного опроса преподавателей, проведённых во время исследования, определяются оценки — вероятности для каждого базового события для конкретной студенческой группы:
‒ P(X1) = 0,3 (30% студентов имеют пробелы в базовых знаниях, необходимых для освоения предмета);
‒ P(X2) = 0,2 (20% студентов имеют низкую учебную мотивацию к предмету);
‒ P(X3) = 0,1;
‒ P(X4) = 0,5;
‒ P(X5) = 0,45;
‒ P(X6) = 0,35.
5. При предположении, что базовые события X1, X2, X3, X4, X5, X6 независимы (упрощение модели), вычисляется вероятность построенной логической функции Y(X1,X2,X3,X4,X5,X6): P(Y) = P ((X1 X2 X3) (X1 X2 X4) (X5 X6)). Вероятности событий «И»:
‒ событие А: P(X1 X2 X3) = P(X1) P(X2) P(X3) = 0,006;
‒ событие B: P(X1 X2 X4) = P(X1) P(X2) P(X4) = 0,003;
‒ событие C: P(X5 X6) = P(X5) P(X6) = 0,158.
Вероятности событий «ИЛИ»: P(Y) = P(A B C) = P(A)+P(B)+P(C) – P(A B) – P(A C) – P(B C)+ P(A) P(B) P(C) = 0,188.
Таким образом, риск неуспеваемости студента первого курса по построенной модели составляет 18,8%.
Построенную модель можно рассмотреть с позиции «Что-если»:
– уменьшение пробелов в базовых знаниях на 20% позволит снизить риск неуспеваемости первокурсника по алгебре на 2% — небольшой эффект;
– при активной работе куратора и благоприятного климата в группе (P(X6) = 0,1) риск неуспеваемости первокурсника по ключевому предмету сокращается на 10.9%. Модель доказывает, что фактор X6 — «Отсутствие поддержки со стороны куратора/одногруппников» — является «узким местом» модели: даже если изначально студент испытывает трудности при обучении, то наличие поддержки со стороны куратора/одногруппников может предотвратить неудачу и помочь первокурсник адаптироваться в вузе. Полученный результат свидетельствует о важности инвестиций в систему тьюторства и кураторства.
Рассчитанную по модели вероятность риска неуспеваемости следует отслеживать в динамике (результаты аттестаций в семестре) и проводить сравнительный анализ с другими группами/курсами, что позволит выявить и повлиять на фактор, который в наибольшей степени оказывает влияние на риск недостижения поставленной педагогической цели.
Логико-вероятностный метод может оказаться полезен при проектировании образовательных программ, диагностики «слабых мест» учебного процесса, оценки индивидуальных образовательных траекторий, управлении качеством образования в вузе/школе. Одна из трудностей при применении логико-вероятностного метода в педагогических исследованиях — вероятностные события педагогической системы достаточно трудно измерить точно (в отличие от технических систем). Для решения этой задачи необходимо использовать систему методов: экспертные оценки, опросы, шкалирование, что позволит в некоторой степени нивелировать влияние субъективного фактора. Зависимость базовых событий — другая сложность применения логико-вероятностного метода в педагогических исследованиях, что существенно усложняет расчёты и требует применения дополнительных исследований. Для этой цели можно использовать байесовские сети — мощный и гибкий инструмент для рассуждений в условиях неопределённости, которые позволяют выйти за рамки статистических моделей , . Построение вероятностной графической модели позволит наглядно отобразить причинно-следственные связи в педагогической системе, интерпретировать их и представить изучаемую систему в понятном и «прозрачном» виде. На основе применения логико-вероятностного метода происходит структурирование знаний о проблеме, выявляются ключевые факторы риска и скрытые взаимосвязи. Гибкая структура метода позволяет обнаружить и по возможности сократить значимые угрозы. Такой подход позволяет управлять образовательными системами более эффективно, отслеживая «слабые места» педагогической системы (например, массовое отчисление).
3. Заключение
На сегодняшний день применение классического логико-вероятностного метода для описания особенностей педагогической системы не является массовым, однако существует значительный пласт исследований, в которых используются близкие подходы: квалиметрический , , вероятностно-статистические модели и педагогическая диагностика , , системный анализ , , анализ рисков в управлении качеством образования , , математическое моделирование и образовательная аналитика , . Систематизировав информацию о возможностях каждого из перечисленных подходов, мы оценили возможный результат их совместной работы с логико-вероятностным методом:
1) квалиметрический подход + логико-вероятностный метод — аппарат для логического структурирования системы, который позволяет учесть неопределённость и стохастичность педагогических процессов (дерево свойств дерево отказов);
2) вероятностно-статистические модели и педагогическая диагностика + логико-вероятностный метод — построение гибких логико-вероятностных моделей, учитывающие особенности педагогической системы;
3) системный анализ в образовании + логико-вероятностный метод — возможность перевода качественного системного понимания на строгий математический язык (получение количественных оценок);
4) анализ рисков в управлении качеством образования + логико-вероятностный метод — возможность перевода управления рисками с уровня субъективных экспертных мнений на уровень количественно обоснованных решений;
5) математическое моделирование и образовательная аналитика + логико-вероятностный метод — мощный комплексный инструмент управления (сбор данных, прогнозирование, глубокий причинный анализ, принятие обоснованных решений).
Таким образом, логико-вероятностный метод способен дополнить традиционные подходы к исследованию педагогической системы. Использование логико-вероятностного метода для анализа педагогической системы позволяет перейти от интуитивных оценок к системному, количественному анализу некоторых проблем, возникающих в сфере образования, принятию обоснованных решений по повышению устойчивости изучаемой системы.
