THEOREM OF STABILITY OF FUZZY SETS
Терновых И.И.
Аспирант, Воронежский Государственный Университет
ТЕОРЕМА ОБ УСТОЙЧИВОСТИ НЕЧЕТКОГО МНОЖЕСТВА
Аннотация
В статье рассматривается устойчивость одного дифференциального уравнения с нечеткой логикой. На основе понятий нечеткой производной выводится α- устойчивость, асимптотическая α- устойчивость.
Ключевые слова: характеристическая функция, нечеткая динамическая система, нечеткая производная, α- устойчивость.
Ternovikh I.I.
Postgraduate student, Voronezh State University
THEOREM OF STABILITY OF FUZZY SETS
Annotation
The stability of differential equation with fuzzy logic is considered. The fuzzy derivative is derived, applied to the solution of fuzzy system equation and derived α- stability and asymptotic α- stability.
Keywords: membership function, fuzzy dynamical system, fuzzy derivative, α- stability, asymptotic α- stability.
- Предварительные условия, обозначения и преобразования.
Пусть 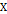 – заданное метрическое пространство, тогда нечёткое подмножество [4]
– заданное метрическое пространство, тогда нечёткое подмножество [4] 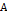
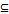
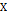 представлено функцией принадлежности
представлено функцией принадлежности 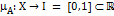 . Семейство всех нечётких подмножеств на
. Семейство всех нечётких подмножеств на 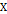 обозначим как
обозначим как 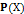 .
.
Слабым 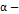 срезом нечёткого подмножества
срезом нечёткого подмножества 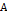
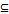
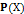 для
для 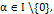 является множество
является множество 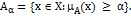
Динамическое поведение непрерывной нечёткой системы, чьё состояние во времени 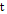 обозначается
обозначается 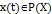 определяется дифференциальным уравнением вида:
определяется дифференциальным уравнением вида:
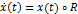 , (1)
, (1)
Где 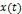
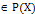 – состояние системы в момент времени
– состояние системы в момент времени  ,
, 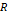 – нечеткое отношение, определяющее переход в следующее состояние, с функцией принадлежности
– нечеткое отношение, определяющее переход в следующее состояние, с функцией принадлежности 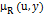 .
.
В терминах функции принадлежности (1) можем переписать в виде:
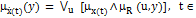 R+
R+
(2)
где 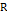 – нечёткое отношение, определенное на
– нечёткое отношение, определенное на 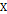 (т.е. нечётком подмножестве
(т.е. нечётком подмножестве 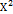 ).
).
Обозначаем определение функции
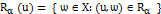 (3)
(3)
принимая во внимание, что, если 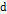 определяет метрику в
определяет метрику в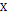 , то для всех
, то для всех 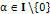 должно быть выполнено следующее [1] :
должно быть выполнено следующее [1] :
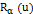 – компактное и непустое,
– компактное и непустое,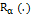 – непрерывное по Липшицу, т.е. существует такое действительное
– непрерывное по Липшицу, т.е. существует такое действительное  , что для всех
, что для всех 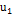 ,
, 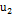 ,
, 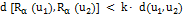 , мы можем показать, что нечёткая система определяется уравнением
, мы можем показать, что нечёткая система определяется уравнением
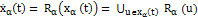 (4)
(4)
которое имеет единственное решение. Другими словами, если 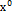 определяет начальное значение, для всех
определяет начальное значение, для всех 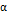 существует такое отображение
существует такое отображение 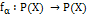 , что
, что
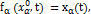 (5)
(5)
и такое отображение 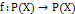 , что
, что
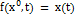 . (6)
. (6)
- Устойчивость
Пусть 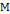 – замкнутое подмножество в
– замкнутое подмножество в 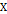 . Для начала вспомним, чтобы избежать потери смысла, определение положительной определённости вещественнозначной функции [1-4].
. Для начала вспомним, чтобы избежать потери смысла, определение положительной определённости вещественнозначной функции [1-4].
Определение1. Функция 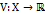 является положительно определённой на множестве
является положительно определённой на множестве 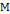 в
в 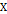 тогда и только тогда, когда:
тогда и только тогда, когда:
-
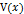 – определена в окрестности множетсва
– определена в окрестности множетсва 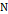 ∈
∈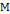 .
. -
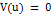 для
для 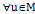 .
. - Для
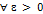 , существует такая
, существует такая 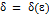 , что
, что 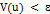 во всех случаях, когда
во всех случаях, когда 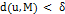 .
. -
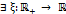 строго возрастающая, непрерывная и такая, что
строго возрастающая, непрерывная и такая, что 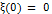 и
и 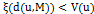 , для всех
, для всех 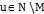 .
.
Отметим, что, так как 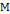 – замкнутое,
– замкнутое, 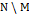 никогда не является пустым. Отсюда, существует такая
никогда не является пустым. Отсюда, существует такая 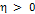 , что
, что
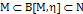 . (7)
. (7)
Ввиду этого, если 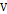 – положительно определенная функция в
– положительно определенная функция в 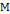 и, если некоторое нечеткое множество
и, если некоторое нечеткое множество 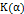 ,
, 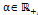 задано следующим образом:
задано следующим образом:
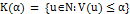 , (8)
, (8)
то всегда возможно найти такую 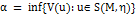 , что
, что 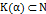 .
.
(сама)
Используя классическое определение устойчивости по Ляпунову [7-8] и работу Терновых И.И [11] получим определение 2.
Определение 2 . Подмножество 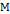
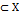 – устойчивое для нечёткой системы
– устойчивое для нечёткой системы  если для всех
если для всех 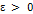 , существует такое
, существует такое 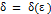 , что
, что 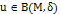 предполагает, что
предполагает, что 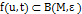 , для всех
, для всех 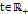 .
.
Определение 3. Подмножество 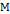
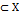 дано как
дано как 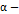 устойчивое для нечёткой системы
устойчивое для нечёткой системы  если для
если для 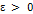 существует такая
существует такая 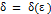 , что
, что 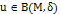 предполагает, что
предполагает, что 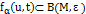 , для всех
, для всех 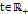 . (сама)
. (сама)
Определение 4. Подмножество 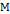
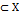 дано как
дано как 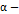 притягивающее (аттрактор) если существует такая окрестность
притягивающее (аттрактор) если существует такая окрестность 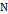
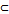
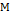 , что для всех
, что для всех 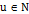 , для всей последовательности
, для всей последовательности 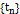 ,
, 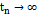 , при
, при 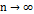 , и всей последовательности
, и всей последовательности 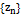 ,
, 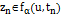 , тогда,
, тогда, 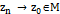 при
при 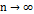 .
.
Можно перефразировать эти два определения так (сама расписала):
- Подмножество
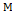
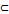
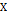 является
является 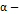 устойчивым тогда и только тогда, когда для всех
устойчивым тогда и только тогда, когда для всех 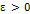 существует такая
существует такая 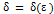 , что
, что 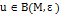 предполагает, что
предполагает, что 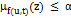 для всех
для всех 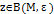 , для всех
, для всех 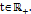
- Подмножество
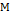
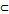
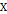 является
является 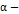 притягивающее (аттрактор) если существует такая окрестность
притягивающее (аттрактор) если существует такая окрестность 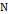
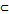
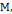 что для всех
что для всех 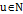 , для всей последовательности
, для всей последовательности 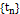 ,
, 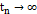 , при
, при 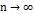 , и всей последовательности
, и всей последовательности 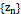 , такой, что
, такой, что 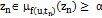 , тогда,
, тогда, 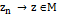 при
при 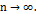
Определение 5. Подмножество 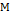 в
в 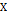 , которое является
, которое является 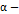 устойчивым и
устойчивым и 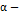 пртягивающим будем называть
пртягивающим будем называть 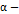 асимптотически устойчивое.
асимптотически устойчивое.
Критерий 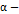 устойчивости для нечёткой системы можно установить через использование понятия нечёткой производной вещественнозначной функции как в работе Де Гласс [1] также будем опираться на труды классической теории дифференциальных уравнений [4].
устойчивости для нечёткой системы можно установить через использование понятия нечёткой производной вещественнозначной функции как в работе Де Гласс [1] также будем опираться на труды классической теории дифференциальных уравнений [4].
Теорема 1. Пусть  – нечёткая система и пусть
– нечёткая система и пусть 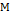 – подмножество
– подмножество 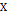 . Если существует такая полунепрерывная снизу функция
. Если существует такая полунепрерывная снизу функция 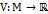 , что
, что
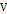 – определяется в окрестности
– определяется в окрестности 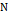

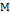 ,
,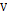 – положительно определённая по отношению к
– положительно определённая по отношению к 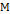 ,
,-
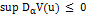 , для всех
, для всех 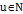 ,
,
тогда 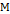 является
является 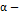 устойчивым.
устойчивым.
Доказательство. Пусть 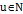 . Так как
. Так как 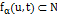 ,
, 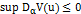 . Следовательно, так как
. Следовательно, так как 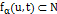 ,
, 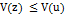 для всех
для всех 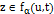 .
.
Пусть 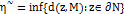 . Тогда, для всех таких
. Тогда, для всех таких  , что
, что 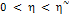
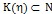 и
и 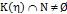 . Пусть,
. Пусть, 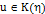 . Предположим, что существует такая
. Предположим, что существует такая  , что
, что 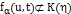 . Тогда, существует такая
. Тогда, существует такая  и
и 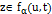 , что
, что 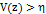 , что является противоречием. Отсюда, для всех
, что является противоречием. Отсюда, для всех 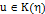 ,
, 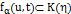 . Таким образом, для всех
. Таким образом, для всех 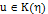 и для все
и для все 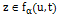 ,
, 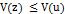 .
.
Так как 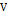 – положительно определённая, для всех
– положительно определённая, для всех 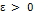 , существует такая
, существует такая 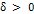 , что
, что 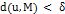 предполагает, что
предполагает, что 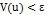 . Тогда, для всех
. Тогда, для всех 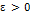 , существует такая
, существует такая 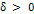 , что
, что 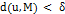 предполагает
предполагает 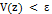 , для всех
, для всех 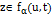 .
.
Более того, согласно Определению 1, для всех 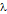 существует такая
существует такая 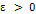 , что
, что 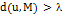 , что предполагает, что
, что предполагает, что 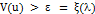 . Отсюда следует, что
. Отсюда следует, что 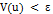 предполагает, что
предполагает, что 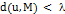 .
.
Таким образом, для всех 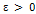 , существует такая
, существует такая 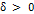 , что
, что 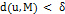 предполагает, что
предполагает, что 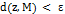 , для всех
, для всех 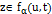 , т.е. такая, что
, т.е. такая, что 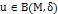 предполагает, что
предполагает, что 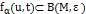 . (сама)
. (сама)
Теорема 2. пусть  – нечёткая система и пусть
– нечёткая система и пусть 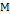 – подмножество
– подмножество 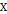 . Если существует такая полунепрерывная снизу функция
. Если существует такая полунепрерывная снизу функция 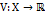 , что
, что
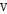 – определяется в окрестности
– определяется в окрестности 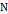

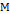 ,
,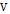 – положительно определённая по отношению к
– положительно определённая по отношению к 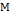 ,
,-
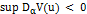 , для всех
, для всех 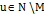
тогда 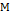 является асимптотически
является асимптотически 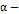 устойчивым.
устойчивым.
Доказательство. Достаточно доказать, что 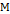 –
– 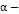 притягивающее. Если предположить, что
притягивающее. Если предположить, что 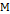 – не
– не 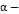 притягивающее подмножество, это предполагает, что существует последовательность
притягивающее подмножество, это предполагает, что существует последовательность 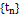 ,где
,где 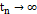 , при
, при 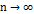 , и такая последовательност
, и такая последовательност 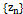 ,что
,что 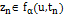 , что
, что 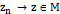 . Тогда,
. Тогда, 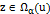 , то есть определенной траектории на
, то есть определенной траектории на 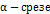 . Также возможно доказать, что
. Также возможно доказать, что 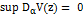 , что является противоречием.
, что является противоречием.
Теоремы 1 и 2 предполагают наличие предварительных знаний об эволюционном уравнении и даже о 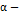 кривых. Поскольку, так чаще всего и есть на самом деле, крайне необходимо иметь возможность переформулировать критерий
кривых. Поскольку, так чаще всего и есть на самом деле, крайне необходимо иметь возможность переформулировать критерий 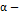 устойчивости таким образом, что более широкие знания об эволюционном уравнении не потребуются.
устойчивости таким образом, что более широкие знания об эволюционном уравнении не потребуются.
References
Glas M. Theory of fuzzy systems.//Fuzzy sets and systems. – 1983. – 10. – P. 65– 77
Е.В. Ивохин, С.О.Волчков. Исследование динамики нечетких дискретных систем //System research & Information Technologies. – 2005. – 4. – P. 94 – 105
Леденева Т.М. Обработка нечеткой информации. – Воронеж.:ВГУ, 2006. – 233 с.
Zadeh A. Lotfi Outline of a new approach to the analysis of complex systems and decision process.// IEEE Transactions on systems, MAN, and Cybernetics, vol. smc – 3, № 1, January,1973
