ON THE PROFILE OF A LIQUID DROP IN TOUCH WITH THE SUBSTRATE
Заславский Ю.М.
C.н.с., д.ф.-м.н. Институт прикладной физики Российской академии наук, Россия, 603950, Нижний Новгород, Ульянова ул., д.46
О ПРОФИЛЕ КАПЛИ ЖИДКОСТИ В КОНТАКТЕ С ПОДЛОЖКОЙ
Аннотация
Проведено теоретическое исследование формы профиля капли жидкости в случаях растекания по твердой ровной смачиваемой подложке и для капли, свисающей с подложки вниз. Граница газ-жидкость рассматривается в условиях равновесия сил поверхностного натяжения и сил гравитации. Проанализирована зависимость радиуса растекания жидкой капли от величины краевого угла для обоих случаев верхнего и нижнего расположения капли.
Ключевые слова: профиль разреза, капля жидкости, поверхностное натяжение, краевой угол, твердая подложка
Zaslavsky Yu.M.
Leader scientist, doctor of p.-m.s., Institute of applied physics Russian academy of science, Russia, 603950, Nizhny Novgorod, Ul’yanov Str., 46.
ON THE PROFILE OF A LIQUID DROP IN TOUCH WITH THE SUBSTRATE
Abstract
Vertical cross sections of a liquid drop spread over a rigid flat wettable substrate and the drop hanging from the substrate are studied theoretically. The gas-liquid boundary analyzed in equilibrium of the surface tension forces and the gravity forces is analyzed. The radius of spreading of a liquid drop as a function of the contact angle is considered for both cases of the upper and lower location of the drop.
Keywords: section profile, liquid drop, surface tension, contact angle, rigid substrate
Известно, что жидкость, растекшаяся по идеально ровной горизонтальной твердой смачиваемой подложке, собирается в капли, которые сохраняют устойчивую форму. Линия границы (профиль) вертикального разреза капли жидкости, удерживающейся в равновесии на идеально гладкой подложке, привлекает внимание исследователей, поскольку информация о форме профиля имеет важное практическое применение [1-5]. В [6] выполнен расчет профиля капли, находящейся в равновесии под действием центробежных сил и сил поверхностного натяжения, когда подложка и капля вращаются вокруг оси симметрии. Там, в частности, показано, что форма капли без вращения, т.е. при действии только сил поверхностного натяжения, представляет собой сферический сегмент.
Теоретический и практический интерес представляет также анализ формы огибающей поверхности капли при отсутствии вращения. Предполагается осесимметричная модель и рассматриваются два случая – капля, растекшаяся поверх твердой ровной горизонтальной подложки, и капля, свисающая с нижней стороны подложки вниз, в которых имеет место равновесие под действием сил тяжести и сил смачивания. В данной статье строится профиль вертикального разреза капли, анализируется зависимость радиуса растекания от величины контактного угла, при этом используется подход, аналогичный предложенному в [6]. Результаты работы могут использоваться в обосновании модели протекания жидкости сквозь вертикальное капиллярное отверстие с последующим срывом капли вниз, анализ которой представлен в работе [7], посвященной расчету периода цикличности капиллярного течения. Рассмотрение начнем со случая нижнего расположения, т.е. со случая капли, висящей под подложкой.
В работе [6] показано, что давление внутри капли, имеющей осесимметричную форму, обусловленное поверхностным натяжением на границе жидкость-пар, описывается выражением
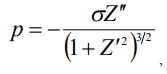 (1)
(1)
где 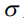 – коэффициент поверхностного натяжения на границе жидкость-пар,
– коэффициент поверхностного натяжения на границе жидкость-пар, 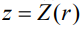 высота огибающей – линии профиля вертикального разреза капли, как функции радиуса,
высота огибающей – линии профиля вертикального разреза капли, как функции радиуса, 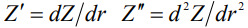 .
.
Записывая условие равновесного состояния капли в поле тяжести, в пренебрежении противодавлением со стороны газовой фазы и под действием сил натяжения, нетрудно показать справедливость уравнения:
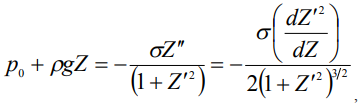 (2)
(2)
интегрируя которое, можно придти к соотношению
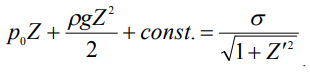 (3)
(3)
При  (где
(где  – полная высота капли) имеет место
– полная высота капли) имеет место 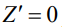 , откуда
, откуда 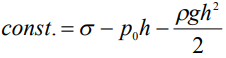 . Аналогичное условие при
. Аналогичное условие при 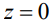 записывается как
записывается как 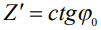 , что позволяет получить выражение для постоянной составляющей давления
, что позволяет получить выражение для постоянной составляющей давления
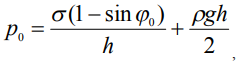 (4)
(4)
где 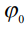 – контактный угол, являющийся вторым из двух параметров (наряду с константой
– контактный угол, являющийся вторым из двух параметров (наряду с константой  ), характеризующим область пересечения трех фаз – подложка-жидкость-пар в «тройной» точке.
), характеризующим область пересечения трех фаз – подложка-жидкость-пар в «тройной» точке.
Раскрывая в (3) корень и интегрируя, приходим к выражению для  , как функции высоты
, как функции высоты 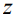 :
:
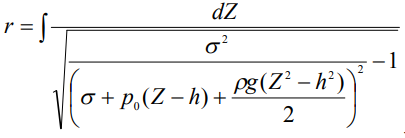 (5)
(5)
Подставляя в (5) выражение 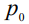 из (4) и переходя к безразмерным
из (4) и переходя к безразмерным 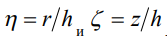 , получаем формулу, на основе которой проводится расчет требуемой функции профиля вертикального разреза
, получаем формулу, на основе которой проводится расчет требуемой функции профиля вертикального разреза
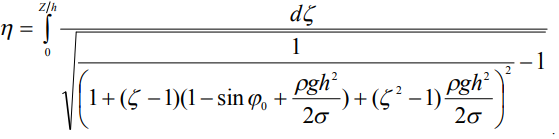 (6)
(6)
Интеграл в (6) сводится к табличному, но ввиду громоздкости результата, расчет профиля и его анализ выполнены численным способом с применением стандартных функций, реализованных в пакете Mathcad. Из расчетных формул (5), (6) следует, что вместо координат 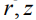 могут использоваться отношения координат к максимальной высоте капли, при этом независимыми параметрами задачи являются величины
могут использоваться отношения координат к максимальной высоте капли, при этом независимыми параметрами задачи являются величины 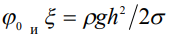 . При графическом построении необходимо строить
. При графическом построении необходимо строить  , как функцию от аргумента
, как функцию от аргумента 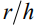 , вычитая текущие значения
, вычитая текущие значения 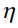 из максимального значения этой величины. Легко также видеть, что переход от рассматриваемого случая капли, свисающей вниз, к случаю верхнего расположения капли, производится сменой знака
из максимального значения этой величины. Легко также видеть, что переход от рассматриваемого случая капли, свисающей вниз, к случаю верхнего расположения капли, производится сменой знака 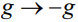 или заменой
или заменой 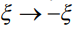 .
.
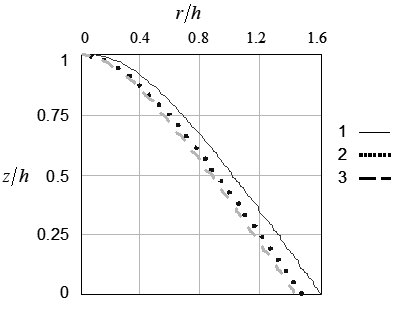
На рис. 1 а представлены профили капли в виде 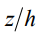 , как функции
, как функции 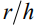 , для нижнего расположения капли (свисающей вниз, ввиду чего ордината также откладывается вниз), при значениях контактного угла
, для нижнего расположения капли (свисающей вниз, ввиду чего ордината также откладывается вниз), при значениях контактного угла 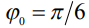 (кривая 1),
(кривая 1), 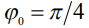 (кривая 2),
(кривая 2), 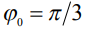 (кривая 3),
(кривая 3), 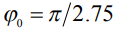 (кривая 4) и при
(кривая 4) и при 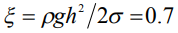 . Последняя из представленных – кривая 4 соответствует предельному значению контактного угла
. Последняя из представленных – кривая 4 соответствует предельному значению контактного угла 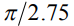 , при котором кривая профиля устойчиво рассчитывается, а радиус растекания минимален. Максимальное значение радиуса растекания в единицах
, при котором кривая профиля устойчиво рассчитывается, а радиус растекания минимален. Максимальное значение радиуса растекания в единицах 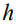 (кривая 1) достигает ~ 0.8. Характерно наличие перегиба в профиле приблизительно на половинной его высоте относительно максимальной высоты
(кривая 1) достигает ~ 0.8. Характерно наличие перегиба в профиле приблизительно на половинной его высоте относительно максимальной высоты 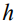 . Можно предположить, что на указанном месте формируется область перетяжки у «набухающей» капли при увеличении ее массы, например, за счет конденсации влаги из соседней паровой фазы. Вероятно, разрыв в профиле и срыв капли вниз, т.е. потеря устойчивости формы, также произойдет в указанной области. Однако такое заключение может быть сделано только на основе решения динамической задачи, хотя на предварительном этапе картина статической равновесной конфигурации также может рассматриваться как пролегомен к анализу динамики.
. Можно предположить, что на указанном месте формируется область перетяжки у «набухающей» капли при увеличении ее массы, например, за счет конденсации влаги из соседней паровой фазы. Вероятно, разрыв в профиле и срыв капли вниз, т.е. потеря устойчивости формы, также произойдет в указанной области. Однако такое заключение может быть сделано только на основе решения динамической задачи, хотя на предварительном этапе картина статической равновесной конфигурации также может рассматриваться как пролегомен к анализу динамики.
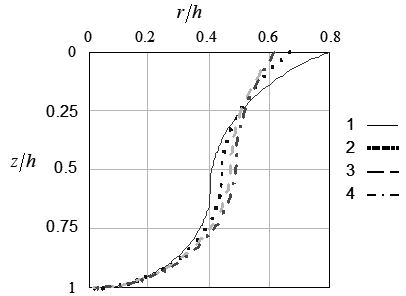
На рис.1 б представлены аналогичные профили капли, соответствующие верхнему ее расположению, т.е. сверху на подложке, при тех же значениях угла смачивания 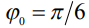 (кривая 1),
(кривая 1), 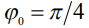 (кривая 2),
(кривая 2), 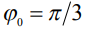 (кривая 3), но при
(кривая 3), но при 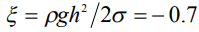 . Здесь имеет место монотонный спад высоты профиля вплоть до нулевого значения с ростом радиуса и достижения им своего максимума – радиуса растекания. Величина радиуса растекания, измеренная в относительных единицах
. Здесь имеет место монотонный спад высоты профиля вплоть до нулевого значения с ростом радиуса и достижения им своего максимума – радиуса растекания. Величина радиуса растекания, измеренная в относительных единицах 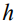 достигает
достигает
|
а
|
|
б
|
|
Рис.1.а – Профиль вертикального разреза капли, свисающей с подложки вниз. Значения контактного угла: Параметр б – Профиль капли, растекшейся по подложке сверху: Параметр |
теперь ~ 1.6, хотя масштабная единица в этом случае может оказаться другой. Если свести к равным значениям не максимальные высоты капель (как это дается на рис.1 а, б для свисающей вниз капли и для лежащей на подложке), а радиусы растекания, то нетрудно заключить, что максимальная высота капли, растекшейся по подложке сверху, меньше в 2 раза, чем у капли, свисающей вниз.
Сравнение профилей вертикального разреза капель жидкости на подложке и свисающей с подложки вниз показывает принципиальное различие их вида и в количественных значениях таких параметров как высота капли и радиус растекания.
Полученные результаты анализа профиля капли, находящейся в контакте с подложкой в условиях равновесия сил гравитации и сил поверхностного натяжения, могут найти применение при проведении фармацевтических исследований, при производстве продуктов питания, а также при выполнении работ, требующих сравнение результатов для обычных условий с теми, которые предполагают отсутствие силы земного тяготения.
References
П.Ж. Де Жен (P. G. De Gennes) Смачивание: Статика и динамика / Успехи физических наук 1987, т.151, вып.4, С. 619-681.
Л.Д. Ландау, Е.М. Лифшиц Гидродинамика. М.: Наука, 1986.
А.В. Лыков Тепломассообмен (Справочник). М.: Энергия, 1978.
В.Н. Николаевский Геомеханика и флюидодинамика с приложениями к проблемам нефтяных и газовых пластов. М.: Недра, 1996.
Ш.Г. Гиматудинов, А.И. Ширковский Физика нефтяного и газового пласта. М.: Альянс, 2005. 309с. (Учебник для ВУЗов изд. 4-е перепечатано с 3-го 1982.)
П.В. Лебедев-Степанов, Т.А. Карабут, Н.А.Чернышев, С.А. Рыбак Исследование формы и устойчивости капли жидкости на вращающейся подложке. //Акуст. ж. 2011. 57, №3, с.323-328
Ю.М. Заславский, В.Ю. Заславский К оценке периода вытекания капель жидкости из капиллярного отверстия // Вестник ННГУ (Математическое моделирование. Оптимальное управление) 2012. №5-2, с.90-92

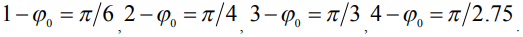
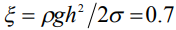 .
.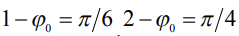 ,
, 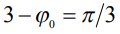 .
.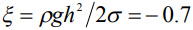 .
.