ON THE ANALYSIS OF DECISION-MAKING PROBLEMS WITH THE HIERARCHICAL STRUCTURE
Митихин В.Г.
Кандидат физико-математических наук, ведущий научный сотрудник, ФГБНУ «Научный центр психического здоровья», Москва
Работа выполнена при поддержке гранта РФФИ № 13-07-00282
К ВОПРОСУ АНАЛИЗА ЗАДАЧ ПРИНЯТИЯ РЕШЕНИЙ С ИЕРАРХИЧЕСКОЙ СТРУКТУРОЙ
Аннотация
В статье рассматриваются примеры анализа многокритериальных задач принятия решений с иерархической структурой, представленные в ряде работ, опубликованных в известных, научных российских изданиях. Разобраны ошибки авторов этих работ, связанные с использованием аппарата метода анализа иерархий и его модификаций.
Ключевые слова: многокритериальные задачи, принятие решений, метод анализа иерархий.
Mitikhin V.G.
PhD in Physics and mathematics, leading researcher, FSBNI «Mental health research center», Moscow
ON THE ANALYSIS OF DECISION-MAKING PROBLEMS WITH THE HIERARCHICAL STRUCTURE
Abstract
This article discusses examples of the analysis of multi-criteria decision-making problems with the hierarchical structure shown in a number of papers published in well-known, Russian scientific publications. Collated mistakes authors of these works related with using tools Analytic Hierarchy Process and its modifications.
Keywords: multi-criteria problem, decision-making, analytic hierarchy process.
Иерархические структуры – методологическая основа для решения задач оптимального выбора альтернатив посредством их многокритериального оценивания. Метод анализа иерархий (МАИ или в оригинальном названии автора метода Т. Саати [1-2] – Analytic Hierarchy Process – AHP) вырос в настоящее время в обширный междисциплинарный раздел теории принятия решений, имеющий убедительные математические и психофизические обоснования и многочисленные приложения. На основе МАИ разработана широко известная программная система Expert Choice (см., например, [3] и там же обширная библиография по зарубежным публикациям МАИ).
Следует отметить, что в начале 70-х годов отечественные авторы Б.Н. Брук и В.Н. Бурков [4] предложили метод обработки экспертной информации для упорядочения объектов, который фактически составляет основу аппарата МАИ. Таким образом, более сорок лет МАИ используется во всем мире (см., например, [1-3] и библиографию в этих работах) для поиска решений в разнообразных ситуациях: от управления на межгосударственном уровне до решения отраслевых и частных проблем практически во всех областях: бизнес, промышленность, здравоохранение, образование и т.д. Число статей прикладного характера с решениями задач из разных областей на основе МАИ измеряется тысячами. Начиная с 1988 г. (раз в два года) проводится Международный симпозиум, посвященный МАИ (International Symposium on Analytic Hierarchy Process, ISAHP), последний (13-ый по счету) состоялся в июне 2014 г. в Вашингтоне (США).
Однако периодически в научной и методической литературе появляются публикации, в которых рассматриваются «контрпримеры» (в этом плане показательны работы [5-6]), целью которых является демонстрация несостоятельности теоретической базы МАИ (разбор этих работ содержится в наших статьях [7-8]), или «примеры» [9-11] использования МАИ, содержащие досадные неточности и ошибки, искажающие возможности МАИ.
Основные положения МАИ, которые обсуждаются в этих (объединим их в категорию «примеры») примерах: фундаментальная шкала МАИ, дескриптивный и нормативный подходы при сравнении элементов иерархии, свертка по критериям.
Анализ указанных примеров-задач показал, что все основные противоречия для этих задач – мнимые и являются следствием заблуждений авторов относительно использования фундаментальной шкалы МАИ, а также отсутствием понимания условий применения дескриптивного и нормативного подходов в МАИ. Этих ошибок можно было бы избежать при условии внимательного прочтения нескольких страниц работы Т. Саати [2, c. 38-46].
- Фундаментальная шкала МАИ
Как известно, для решения задач в рамках МАИ экспертами формируются так называемые матрицы парных сравнений А = (aij). Элементы матриц А получаются на основе измерения предпочтений экспертов в шкале отношений, в частности, используется универсальная фундаментальная шкала (в первую очередь она используется для сравнения объектов по качественным критериям). Фундаментальная шкала измерения результатов парных сравнений, используемая в МАИ, была получена на основе базовых соотношений модели нервного возбуждения, которые приводят к известному психофизиологическому закону «стимул-реакция». Эффективность этой шкалы была проверена во многих приложениях (см., прежде всего, работы [1-3]), а также путем сравнения с другими шкалами при решении тестовых практических задач, решения которых были заранее известны.
Для облегчения работы эксперта основные деления фундаментальной шкалы имеют соответствующую смысловую интерпретацию: 1 – равная важность; 3 – слабое превосходство; 5 – превосходство; 7 – сильное превосходство; 9 – абсолютное превосходство; 2, 4, 6, 8 – промежуточные случаи. Шкала содержит и соответствующие обратные значения (для измерения результатов обратных парных сравнений).
Формальное применение фундаментальной шкалы МАИ, которая является шкалой отношений, приводит к следующим типичным примерам (цитируем, например, из работы [9, с. 130]): «…пусть, например, объект р1 абсолютно превосходит объект р2 и a12 = 9 согласно шкале. Пусть также объект р2 абсолютно превосходит объект р3 и, следовательно, a23 = 9. Спрашивается, какое число назовет пользователь в качестве a13 – тоже 9 или 81? Последнее число в шкале отсутствует».
Простое решение этого противоречия состоит в том, что, что если эксперт использует классическую фундаментальную шкалу (1; 9), то он обязан использовать абсолютную степень превосходства (т.е., назвать число 9). При этом, вообще говоря, возникает рассогласование результатов измерений, но это явление связано практически с любыми измерениями, тем более с измерениями на уровне психофизиологических реакций. Если же есть возможность использовать обычную шкалу отношений (например, объекты сравниваются на основе количественного критерия типа «расстояние»), то результат может измеряться в обычной шкале отношений (при этом результат измерения может оказаться практически любой положительной величиной) и при этом возникают «идеально согласованные» матрицы парных сравнений.
Дополнительно отметим, что в МАИ имеются приемы (см., [2]), позволяющие, с одной стороны, осмысленно расширить границы фундаментальной шкалы и перейти от классического случая (1; 9) к интервалу (1; ∞), а с другой – повысить точность измерения на любом интервале оценок, используя, например, значения 1.1, 1.2, …,1.9 на интервале (1; 2). Ознакомиться с этими процедурами можно по работе Т. Саати [1, с. 38]. Такой подход можно использовать для выявления тонких различий объектов сравнения, а также для еще более тонких, например, на интервале (1.1 ; 1.2).
Отметим, что отсутствие четко описанного измерительного инструмента (доступного любому пользователю) для сравнения объектов, аналогичного фундаментальной шкале МАИ, помешало авторам пионерской работы [4] внедрить свой метод в практику решения многокритериальных задач и, фактически, уступить приоритет в пользу МАИ. В аналогичной ситуации оказались авторы работы [12], предлагающие использовать свой «метод важности критериев», который следует расценивать как весьма неудачную (как по названию, так и по содержанию, на что указывает наш анализ [7-8]) модификацию МАИ, для решения многокритериальных задач. Критику МАИ и, в частности, фундаментальной шкалы, авторы [12] строят на своих ошибочных работах [5-6] и некоторых «требованиях математической теории измерений», известных только этим авторам, но никакого разумного измерительного инструмента (доступного любому пользователю) они предложить не могут. Для иллюстрации «доказательного стиля» авторов работ [5-6; 12] можно привести прямую цитату (например, из работы [6, с. 77]), касающуюся измерений в шкале порядка: «Предположим, что имеется информация о том, что рост предпочтений вдоль шкалы критериев замедляется: при переходе от шкальной оценки m к оценке g предпочтения возрастают больше, чем при переходе от оценки g к e…». Весьма интересно, как авторы делают эти измерения в порядковой шкале и ещё интереснее, как они смогут изложить этот алгоритм измерения неискушенному пользователю? Но такие измерения роста предпочтений четко описываются в шкале отношений, к которой относится и фундаментальная шкала МАИ, которую авторы указанных работ не считают «научно обоснованной».
Непонимание авторами примеров из работ [5-6; 9; 12] сути и возможностей фундаментальной шкалы, элементарно описанных Т. Саати в [2] буквально на 2-х страницах, приводит их к выводу о несостоятельности МАИ.
- Дескриптивный и нормативный подходы в МАИ
Аргументируя свой выбор дескриптивного подхода для решения примера в статье [5], авторы в следующей статье [6] ссылаются на классическую «задачу о покупке дома» из книги Т. Саати [2, с. 40-44], которая, якобы решается «параллельно двумя подходами». По мнению авторов [6] –упомянутые в книге [2] подходы не что иное, как дескриптивный и нормативный подходы и по логике авторов [5-6] – это означает, что выбор подхода решения задачи в рамках МАИ произволен, если сам Т. Саати подобное демонстрирует.
Здесь авторы статьи [6] допустили элементарную ошибку, они не разобрались в ситуации: «задача о покупке дома» решена с помощью одного дескриптивного подхода, но с использованием двух способов (названные в книге [2, с. 44] – распределенный способ и идеальный способ) вычисления глобальных приоритетов. Различие этих способов состоит в том, что в идеальном способе перед заключительной операцией вычисления глобальных приоритетов (суммирование весов альтернатив по критериям с учетом веса каждого критерия) добавляется нормирование весов по каждому критерию с помощью деления на максимальный вес альтернативы по соответствующему критерию. То есть, при этом нормировании альтернативы получают предварительные веса (по каждому критерию) относительно наилучшей альтернативы (из рассматриваемых альтернатив). Эта операция нормирования и была ошибочно воспринята авторами [6] за использование нормативного подхода.
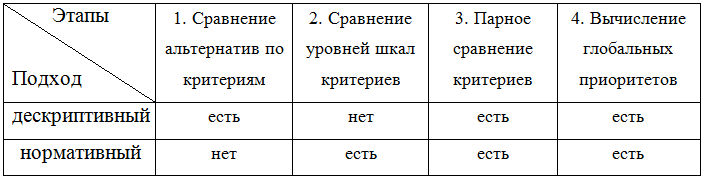
Для наглядности приведем в таблице 1 основные этапы для дескриптивного (описательного) и нормативного подходов в задачах, решаемых на основе МАИ.
Таблица 1 - Основные этапы для дескриптивного и нормативного подходов МАИ
То есть, первым отличительным признаком нормативного подхода (по сравнению с дескриптивным подходом) является отсутствие этапа 1 (парные сравнения альтернатив по критериям). В «задаче о покупке дома» любой внимательный читатель обнаружит этап 1 (т.е., признак дескриптивного подхода!) в книге [2, с. 43] и, соответственно, не найдет этапа 2.
Добавим, что для корректного применения нормативного подхода должно выполняться необходимое условие: шкалы критериев, а точнее уровни этих шкал, должны быть однозначно описаны. В «задаче о покупке дома» это условие не выполняется, например, для первого критерия: «Размер дома» – это составной, размытый критерий, который включает: число и размер комнат, подсобную и общую площадь, поэтому в такой постановке задачи возможно использование только дескриптивного подхода.
В книге Т. Саати [2, с. 45-46] сразу после «задачи о покупке дома» приводится «задача о повышении зарплаты служащим», которая решается с помощью нормативного подхода.
Мы приведем по этому поводу лишь одно предложение из работы Т. Саати [2, с. 45]: «Нормативный подход проявляется в использовании экспертных суждений для создания шкалы интенсивностей (лингвистических стандартов), которую можно применять для раздельной оценки вариантов по одному».
Возвращаясь к примеру-1, подробно описанному в статьях [5-8], отметим, что критерии f1 и f2 имеют общую ординальную (порядковую) шкалу оценок (однозначных уровней шкалы): e – отлично, g – хорошо, m – посредственно, т.е., такие оценки с очевидностью предполагают сравнение рассматриваемых вариантов с некоторым стандартом по этим критериям. Поэтому выбор здесь нормативного подхода адекватен задаче и, кроме того, обеспечивает ряд полезных характеристик решения и процесса решения, среди которых – сохранение порядка ранжировок при добавлении или удалении альтернатив, сокращение объема операций для получения решения. Поясним последнее: для примера-1 в статье [5] нужно было ранжировать 4 альтернативы, при этом дескриптивный подход потребовал обработки 2-х матриц размера 4 (матрицы парных сравнений 4-х альтернатив по 2-м критериям). Нормативный подход, предложенный в нашей работе [7] для решения этой задачи, использовал обработку лишь одной матрицы размера 3 (матрица парных сравнений 3-х уровней шкалы). Если бы в этой задаче нужно было ранжировать полное число альтернатив, а их – 9, то дескриптивный подход потребует обработки уже 2-х матриц 9-го порядка, а нормативный подход использует ту же самую матрицу 3-го порядка. Очевидно, что рост числа критериев обеспечивает рост числа возможных альтернатив по экспоненте, что делает весьма проблематичным в таких ситуациях использование дескриптивного подхода (и ординальных теорий типа «теории важности критериев»). Напротив, при нормативном подходе максимальный размер матриц парных сравнений при создании шкал интенсивностей определяется только числом уровней шкалы критерия, которое на практике, как правило, не более 10.
Для того чтобы вскрыть основную ошибку авторов [5-6] при решении примера-1 отметим существенный момент приведенного в [5-6] ошибочного решения. А именно: параметры решения а и b (а – степень превосходства в предпочтительности оценки e над оценкой g ; b – степень превосходства оценки g над оценкой m . При этом, а > 1 и b > 1) определяют только взаимное соотношение оценок общей ординальной шкалы критериев. Но важная информация о том, что в этой ординальной шкале существует максимальная, абсолютно лучшая оценка (e – отлично) при выбранном в [5-6] варианте дескриптивного подхода не используется. Для учета этого обстоятельства и получения корректного решения примера-1 необходимо использование нормативного подхода МАИ, что и было сделано нами в работе [7].
- Линейная свертка по критериям в МАИ
Решение многокритериальных задач в МАИ основано на использовании линейной свертки критериев. Здесь мы не будем обсуждать теоретические аспекты условий обоснованности (или необоснованности) этого приема. Цель нашей работы – обсуждение соответствующих «контрпримеров». В частности, в работе [10], посвященной изложению «упрощенного варианта МАИ» на основе нелинейной свертки критериев, рассматривается пример, решение которого на основе «классического» варианта МАИ приводит к результату, противоречащему (по мнению автора [10]) здравому смыслу. Приведем этот пример и его решение в авторской формулировке:
«Предположим, что задача состоит в выборе (например, с целью приобретения) прямоугольного земельного участка из следующих трех вариантов: 10 * 10; 5 * 20 и 7 * 15, измерение производится в каких-то единицах длины. Очевидно, площади двух первых участков одинаковы и меньше площади третьего участка. Нетрудно проверить (например, чисто геометрически), что третий участок (площадь которого максимальна!) ни при каких положительных весах w1, w2 критериев, которыми являются длина и ширина участка (выделено курсивом нами), не может оказаться выбранным, если выбор осуществляется при помощи линейной свертки критериев».
На наш взгляд, «противоречие здравому смыслу» здесь базируется на элементарной логической ошибке автора [10]. Действительно, выбор участков производится по критериям длины и ширины, а результат оценивается по другому критерию – площадь участка. Заметим, что это качественно другой важный критерий (как с точки зрения обычного пользователя, так и по физической размерности), который в процессе выбора не принимается в расчет (если же площадь участка учитывать в процессе выбора, то никаких противоречий не возникает). В рамках рассматриваемого примера, используя логику автора [10] можно привести еще более яркое «противоречие здравому смыслу»: если сделать участки очень узкими (при той же площади), то можно получить результат в виде участка, на котором в буквальном смысле нельзя стоять без нарушения его границ.
В заключение опишем ещё один пример, который из-за продемонстрированной авторами работы [11] алогичности (понятной на уровне элементарного владения русским языком) стоит вне всякой корректности использования МАИ. Тема статьи [11] достаточно серьёзная: «О стратегии развития и модернизации РАН» и не оставляет возможности для шуток в духе Мигдала-Ландау. Авторы достаточно интересно и грамотно описывают альтернативные стратегии развития и модернизации РАН и предлагают использовать МАИ для решения поставленной задачи выбора оптимальной стратегии. Они приводят следующие соображения в качестве обоснования выбора метода решения: «Метод особенно хорош для решения сложных проблем группой людей и применяется много лет в сотнях зарубежных организаций. Его особенности, достоинства и недостатки также обсуждаются в ряде работ, из которых мы рекомендуем недавние статьи Подиновских». Эти статьи [5-6] выше мы уже обсуждали и для удобства читателя напомним только их названия: «О некорректности метода анализа иерархий» и «Еще раз о некорректности метода анализа иерархий», из которых уже с очевидностью следует, что Подиновские имеют совершенно определенное мнение о МАИ. Остается загадкой, что побудило авторов [11] рекомендовать для знакомства с МАИ статьи [5-6], которые находятся в явном диссонансе (уже хотя бы по названиям!) с работой [11].
Литература
- Saaty T.L. The analytic hierarchy process. – N.-Y.: McGraw Hill, 1980. – 288 p.
- Саати Т. Л. Принятие решений при зависимостях и обратных связях: Аналитические сети. – М.: Изд. ЛКИ, 2008. – 360 с.
- Ishizaka A., Labib A. Analytic Hierarchy Process and Expert Choice: Benefits and Limitations, ORInsight, 22(4), p. 201–220, 2009.
- Брук Б.Н., Бурков В.Н. Методы экспертных оценок в задачах упорядочения объектов // Известия АН СССР. Техническая кибернетика. 1972, № 3, с. 29 – 39.
- Подиновский В.В., Подиновская О.В. О некорректности метода анализа иерархий // Проблемы управления. 2011, № 1, с. 8 – 13.
- Подиновский В.В., Подиновская О.В. Еще раз о некорректности метода анализа иерархий // Проблемы управления. 2012, № 4, с. 75 – 78.
- Митихин В.Г. Об одном контрпримере для метода анализа иерархий // Проблемы управления. 2012, № 3, с. 77–79.
- Митихин В.Г. Еще раз о корректности метода анализа иерархий. Материалы IV межд. научно-практ. конференции «Фундаментальные и прикладные науки сегодня», 20-21.10.2014, North Charleston, USA, т. 1, с. 188-194.
- Черноруцкий И.Г. Методы принятия решений. – СПб.: БХВ-Петербург, 2005, 416 с.
- Ногин В.Д. Упрощенный вариант метода анализа иерархий на основе нелинейной свертки критериев // Ж. вычисл. матем. и матем. физ. 2004, т. 44, № 7. с. 1261-1270.
- Вайнмахер А.М., Шмерлинг Д.С. О стратегии развития и модернизации РАН. Материалы XII-го Всероссийского совещания по проблемам управления, Москва 16-19 июня 2014, с. 8004-8011.
- Подиновская О.В., Подиновский В.В. Анализ иерархических многокритериальных задач принятия решений методами теории важности критериев // Проблемы управления. 2014, № 6, с. 2 – 8.
References
- Saaty T.L. The analytic hierarchy process. – N.-Y.: McGraw Hill, 1980. – 288 p.
- Saaty, T. L. Decision Making with Dependence and Feedback: The Analytic Network Process (Second ed.). Pittsburgh, USA, 2001, 350 р.
- Ishizaka A., Labib A. Analytic Hierarchy Process and Expert Choice: Benefits and Limitations, ORInsight, 22(4), p. 201–220, 2009.
- Bruk B.N., Burkov V.N. Metody ekspertnykh otsenok v zadachakh uporyadocheniya ob"ektov // Izvestiya AN SSSR. Tekhnicheskaya kibernetika. 1972, № 3, s. 29 – 39.
- Podinovski V.V., Podinovskaya O.V. On the theoretical incorrectness of the analytic hierarchy // Control Sciences, 2011, № 1, p. 8-13.
- Podinovski V.V., Podinovskaya O.V. Another note on the incorrectness of the analytic hierarchy // Control Sciences, 2012, № 4, p. 8-13.
- Mitikhin V.G. On a counterexample for the analytic hierarchy process // Control Sciences, 2012, № 3, p. 77-79.
- Mitikhin V.G. Eshche raz o korrektnosti metoda analiza ierarkhii. Materialy IV mezhd. nauchno-prakt. konferentsii «Fundamental'nye i prikladnye nauki segodnya», 20-21.10.2014, North Charleston, USA, t. 1, s. 188-194.
- Chernorutskii I.G. Metody prinyatiya reshenii. – SPb.: BKhV-Peterburg, 2005, 416 s.
- Nogin V.D. Uproshchennyi variant metoda analiza ierarkhii na osnove nelineinoi svertki kriteriev // Zh. vychisl. matem. i matem. fiz., 2004, t. 44, № 7. s. 1261-1270.
- Vainmakher A.M., Shmerling D.S. O strategii razvitiya i modernizatsii RAN. Materialy XII-go Vserossiiskogo soveshchaniya po problemam upravleniya, Moskva 16-19 iyunya 2014, s. 8004-8011.
- Podinovskaya O.V., Podinovski V.V. Analysis of hierarchical multicriterial decision making problems using methods of criteria importance theory // Control Sciences, 2014, № 6, p. 2-8.