THE EFFECT OF PARTICLE-HOLE INTERACTION TO THE ENERGY SEPARATION OF PROTONS AND NEUTRONS IN FAMILIES MIRROR NUCLEI AT NEARLY SYMMETRICAL
Ершов Д. К.
Кандидат физико-математических наук, Смоленский государственный университет
ЭФФЕКТ ЧАСТИЧНО-ДЫРОЧНОГО ВЗАИМОДЕЙСТВИЯ ДЛЯ ЭНЕРГИИ ОТДЕЛЕНИЯ ПРОТОНОВ И НЕЙТРОНОВ В ЗЕРКАЛЬНЫХ ЯДРАХ, БЛИЗКИХ К СИММЕТРИЧНЫМ
Аннотация
Используя экспериментальные данные рассчитаны энергия отделения протонов и нейтронов в зеркальных ядрах с Z=N±1. Энергии отделения из нечетных подоболочек больше, чем из четных. После Z≥32 эта аномалия исчезает.
Ключевые слова: зеркальные ядра, протоны, нейтроны, энергии отделения, частично-дырочное взаимодействие.
Ershov D. K.
Candidate of Physical and Mathematical Sciences, Smolensk State University.
THE EFFECT OF PARTICLE-HOLE INTERACTION TO THE ENERGY SEPARATION OF PROTONS AND NEUTRONS IN FAMILIES MIRROR NUCLEI AT NEARLY SYMMETRICAL
Abstract
By the used of experimental date are calculated an energy separation for the protons and neutrons in the family mirror nuclei with Z=N±1. Of the energy separation from nuclei with odd nucleon subshell is the more then with even subshell. This anomaly vanish after Z≥32.
Keywords: mirror nucleus, protons, neutrons, energy branch, particle-hole interaction.
- Introduction
At present time, there are no unified microscopic theory, which from first principles explains all the properties of atomic nuclei. [1, 2]
This is largely due to the fact that the atomic nuclei even medium-sized, and even more heavy elements, are multiparticle systems consisting of strongly interacting nucleons. Therefore, for the study of nuclear properties, processes of nuclear interactions has to use different semiempirical approaches appropriate to different model representations (mean-field theory, shell model, model of pair interactions). It should be noted that the finite of the sizes of nuclei leads to additional difficulties in their theoretical description. Infinite system turns out to be easier to describe. A special place among the famous atomic nuclei occupy so-called mirror nuclei. This pair of nuclei which the number of neutrons in one equals the number of protons in another N1=Z1 and conversely N2=Z1.
In such nuclei in the most refined can explore some nuclear effects - for example, energy symmetry which ~(N-Z)2.
In this paper calculates the energy separation of protons Sp and neutrons Sn in families mirror nuclei with Z=N±1.
- Methodology
Energy separation are determined by the known method
Sp(Z,N)=M(Z-1,N)+MH-M(Z,N) (1)Sp(Z,N)=M(Z,N-1)+MH-M(Z,N) (2)
Here M is the mass of the relevant isotopes, Mn - the mass of a neutron, MH - mass of hydrogen atoms. Often, instead of a mass of use value (M-A). The final results for Sp and Sn, is not change as a consequence of the conservation of baryon charge (in this case A).
If you use the available experimental data [3, 4] for the corresponding mirror nuclei up Z=40, you can calculate the energy separation Sp and Sn.
- Results and Discussion
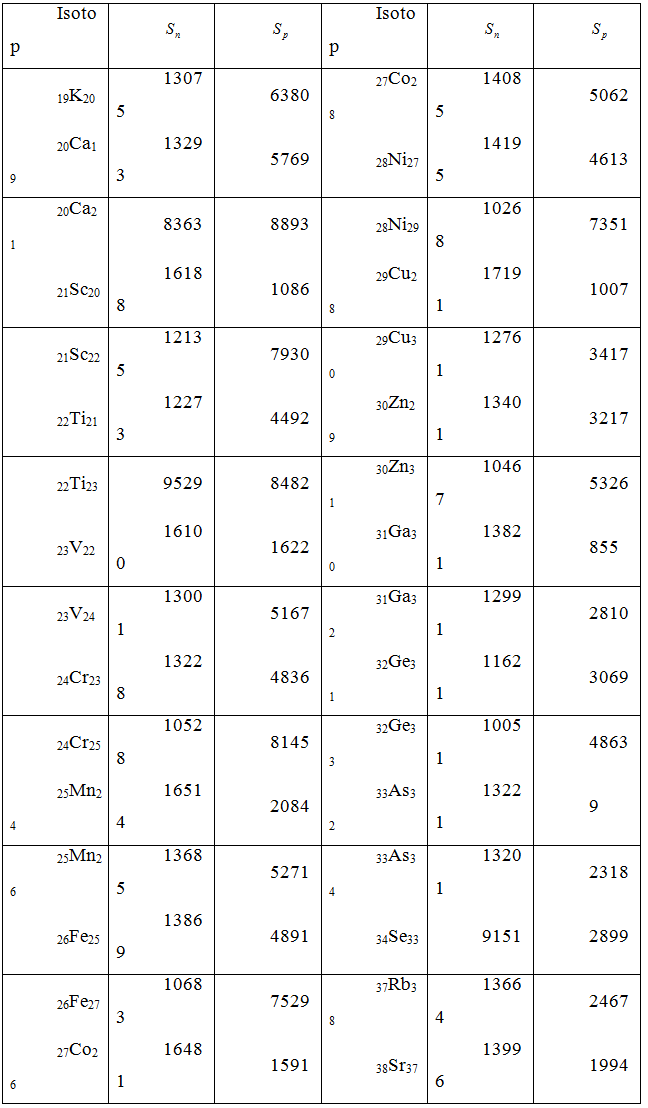
The results of calculations are presented in the table.
Table 1 - Energy separation (in Kev).
Calculations were done for Z=12 ÷ 40, but in order to save we give the values only for the most interesting area of values Z.
The results of calculations shows that for some couples mirror nuclei is observed anomaly: energy separation Sp and Sn for odd subhell exceed the corresponding value for even subhell. After Z=32 this anomaly disappears (except for a pair of ![]() and
and ![]() ). It is easy to notice, that all «normal» pair in the model clustering can be presented as mα+1H0 or mα+0n1, and all abnormal pairs in the form mα+1H2 or mα+2He1, m- the number of α particles (2He2).
). It is easy to notice, that all «normal» pair in the model clustering can be presented as mα+1H0 or mα+0n1, and all abnormal pairs in the form mα+1H2 or mα+2He1, m- the number of α particles (2He2).
The fact that the energy separation of a single of the valence neutrons and protons is less than the energy separation of nucleons from closed subhell 2He2 quite understandable. But why energy separation of protons from 2He1 less energy separation of proton from 1H2, and energy separation of neutrons from 1H2 less energy separation of protons from 2He1 not entirely clear. Of course, the shell model are its sphere application and the nucleons are moving in a self-consistent field all other nucleons, but the effects pairing of identical nucleons in nuclei have long been considered established.
You should pay attention to the fact that the anomaly disappears after Z=32. In this area, the binding energy of nucleons reach maximum (nuclear saturation).
The biggest specific binding energy of the nucleus 28Ni28, but this nucleus is specific - it doubly magic. In the recent paper [5] it is stated that the correlation effects are maximized at Z=32.
It is also interesting to note that ![]() and
and ![]() may be regarded as a respectively with proton and neutron holes. Particle-hole interaction actively used in various variants of modern microscopic theory of the nucleus [1, 2], and the anomaly may reflect the changing nature of the interaction of the particle-hole state in the region Z=32 in the mirror nuclei.
may be regarded as a respectively with proton and neutron holes. Particle-hole interaction actively used in various variants of modern microscopic theory of the nucleus [1, 2], and the anomaly may reflect the changing nature of the interaction of the particle-hole state in the region Z=32 in the mirror nuclei.
Quartet (actually α partial) clustering symmetric (Z=N) nuclei in was considered in [6]. There was studied isovector pairing - alpha-particle presented as a system of two isovector pairs.
It should be noted that in the vicinity of the magical Z=28 no radical changes are taking place. These changes are observed at Z≥32 when filling starts proton 1f5/2 subshell. It ends with Z=38, and then begins the collectivization filled (intruders) configuration of high orbits. It leads, for example, to the absence of closed subshell when Z=40, Z=40, [7]. Perhaps the single return anomalies for 37Rb38 and 38Sr37 related to the end of filling subshell.
4.Conclusion
In conclusion, we note that, perhaps for the first time showed the influence of the particle-hole interaction to the energy separation of the nucleons in the mirror nuclei. It is interesting to investigate and other characteristics of these mirrored pairs on the influence of these anomalies.
Литература
- МигдалА. Б. Теория конечных Ферми-систем и свойства атомных ядер. М.: Наука, 1983.
- СоловьевВ. Г. Теория атомных ядер – квазичастицы и фононы. М.: Энергоатомиздат, 1989.
- Физические величины. Справочник. М.: Энергоатомиздат, 1991.
- Атомные массы, 2011.
- Porquet M.-G. and Sorlin O. Phys. Rev. C85.014303 (2012)
- Sanduliscu N., Neqrea D., Dukelsky J. and Johnson C.W. Phys. Rev. C85.061303 (2012)
- Naimi S. G. Audi, Beek D., Blaum K. et all. Phys Rev. C85.014325 (2012)
References
- Migdal A. B. Teorija konechnyh Fermi-sistem i svojstva atomnyh jader. M.: Nauka, 1983.
- Solov'ev V. G. Teorija atomnyh jader – kvazichasticy i fonony. M.: Jenergoatomizdat, 1989.
- Fizicheskie velichiny. Spravochnik. M.: Jenergoatomizdat, 1991.
- Atomnye massy, 2011.
- Porquet M.-G. and Sorlin O. Phys. Rev. C85.014303 (2012)
- Sanduliscu N., Neqrea D., Dukelsky J. and Johnson C.W. Phys. Rev. C85.061303 (2012)
- Naimi S. G. Audi, Beek D., Blaum K. et all. Phys Rev. C85.014325 (2012)