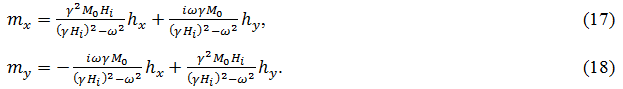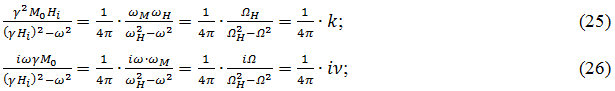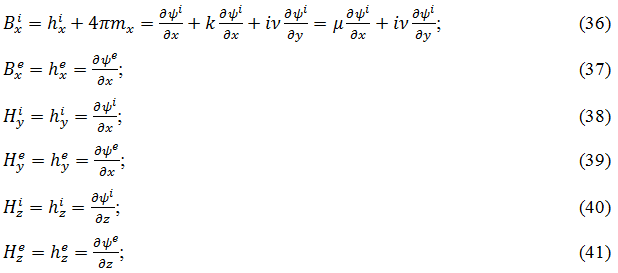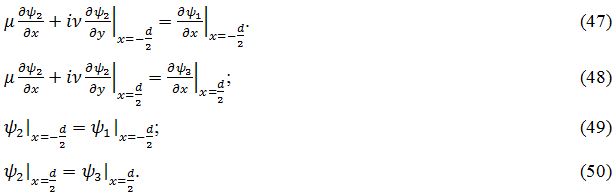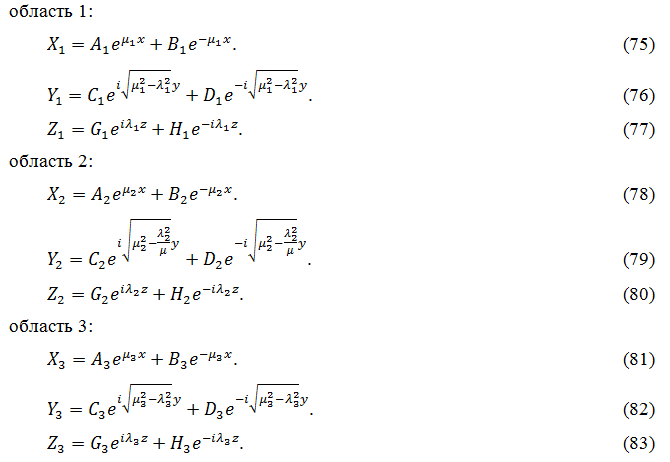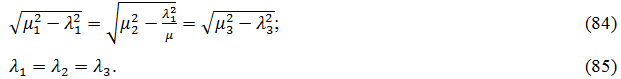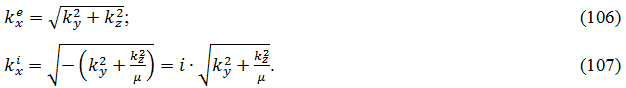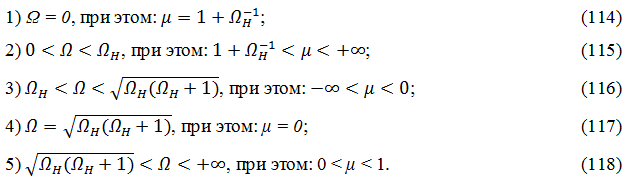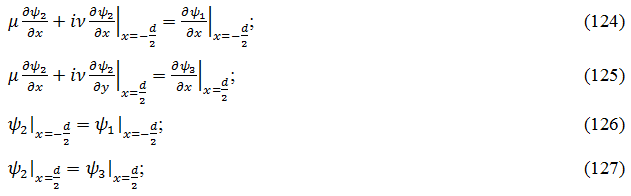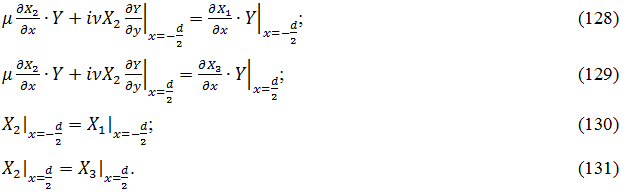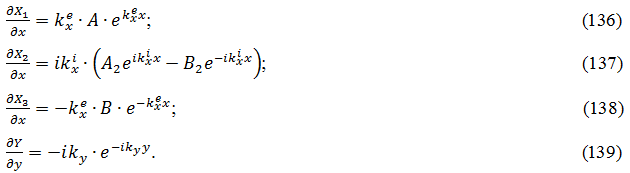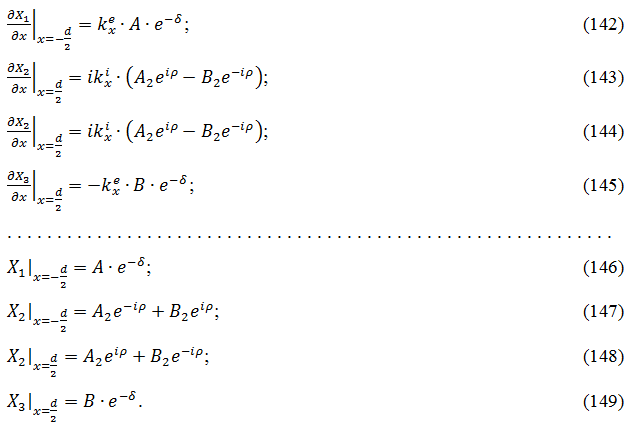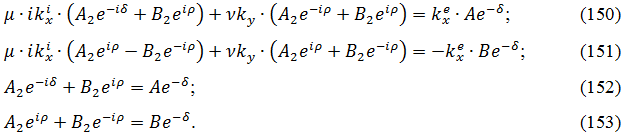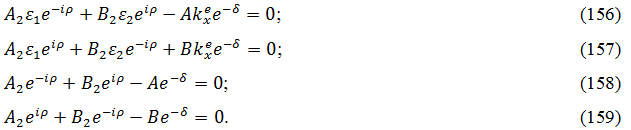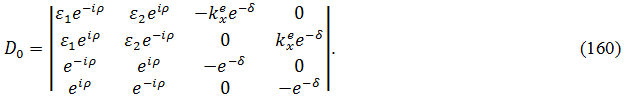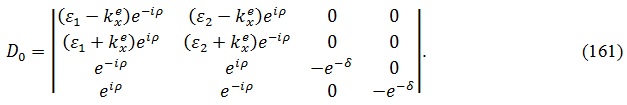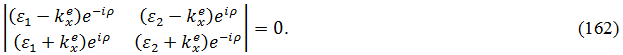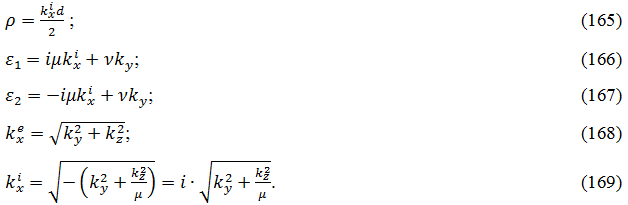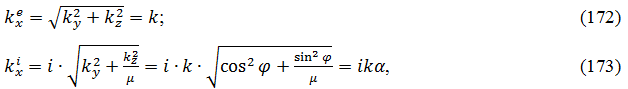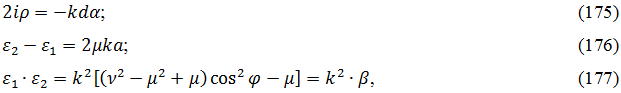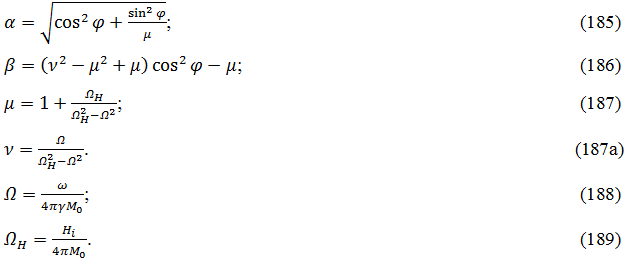CALCULATION OF DISPERSION CHARACTERISTICS OF MAGNETOSTATIC WAVES IN FERRITE FILM IN SCILAB APPLICATION
Богачук Д.В.1, Власов В.С.2
1Магистрант, 2Кандидат физико-математических наук, Сыктывкарский государственный университет имени Питирима Сорокина
РАСЧЕТ ДИСПЕРСИОННЫХ ХАРАКТЕРИСТИК МАГНИТОСТАТИЧЕСКИХ ВОЛН В ФЕРРИТОВОЙ ПЛЕНКЕ В ПАКЕТЕ SKILAB
Аннотация
В статье приводится расчет дисперсионных характеристик магнитостатических волн, распространяющихся в ферритовой пленке. В пакете Scilab смоделированы характеристики волн при различных начальных параметрах (таких как величина внешнего поля, намагниченность и толщина пленки).
Ключевые слова: магнитостатические волны, дисперсионные характеристики, ферритовые пленки.
Bogachuk D.V.1, Vlasov V.S.2
1 Candidate for a master’s degree, 2PhD in Physics and Mathematics, Syktyvkar State University
CALCULATION OF DISPERSION CHARACTERISTICS OF MAGNETOSTATIC WAVES IN FERRITE FILM IN SCILAB APPLICATION
Abstract
The article describes the calculation of dispersion characteristics of magnetostatic waves propagating in ferrite film. The characteristics of these waves were modeled considering various initial conditions (such as external field magnitude, magnetization intensity and film thickness) using Scilab application.
Keywords: magnetostatic waves, dispersion characteristics, ferrite films.
Введение
Задача теоретического исследования магнитостатических волн представляет большой научный и практический интерес в связи с перспективами миниатюризации элементной базы радиоэлектроники СВЧ на основе магнитостатических волн и колебаний.
Одним из наиболее интенсивно развивающихся в настоящее время направлений твердотельной волновой электроники является спин-волновая электроника, предмет изучения которой составляют магнитостатические волны (МСВ) в ферромагнетиках. Магнитостатические волны обладают рядом уникальных возможностей (зависимость дисперсионных свойств от величины и направления внешнего постоянного поля подмагничивания, сравнительно низкая групповая скорость), которые позволяют создавать на их основе самые разнообразные элементы СВЧ тракта: линии задержки, фильтры, невзаимные устройства и другие, имеющие характеристики, принципиально нереализуемые в диапазоне частот 1÷20 ГГц на основе электромагнитных или акустических волн [1].
Техника магнитостатических волн (МСВ) представляется перспективной для создания устройств с рабочими частотами СВЧ-диапазонов и мгновенной ширины полосы до 1 ГГц. Эта техника основана на распространении МСВ в монокристаллических ферромагнитных пленках, таких как пленки железоиттриевого граната (ЖИГ), и является физической основой целого ряда планарных устройств для распознавания, контроля и обработки сигналов непостредственно в сантиметровом диапазоне частот [2]. В результате отпадает необходимость в СВЧ-смесителях, традиционно применяемых для "переноса" входящих сигналов в более низкочастотный (УВЧ) диапазон, в котором могут быть использованы уже другие устройства.
Распространение магнитостатических волн
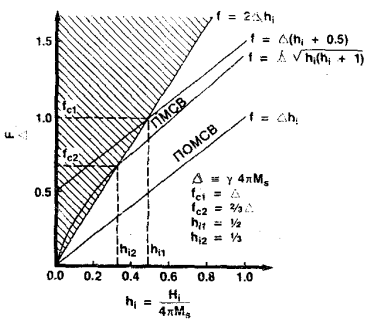
Вопросы распространения МСВ в безграничной пленке ЖИГ широко освещены в литературе [3]. В зависимости от взаимной ориентации магнитного поля смещения, направления распространения волны и самой пленки, в ней могут распространяться три чистые моды МСВ: поверхностная магнитостатическая волна (ПМСВ), прямая объемная магнитостатическая волна (ПОМСВ) и обратная объемная магнитостатическая волна (ООМСВ). Частотные границы существования перечисленных мод МСВ показаны на рис. 1. Всем трем типам присуща дисперсия.
Рис. 1 - Частотные границы МСВ (границы для ПОМСВ и ООМСВ одинаковы)
Дисперсионное соотношение. Решение Дэймона-Эшбаха
Уравнения магнитостатики:
Предположим, что поле и намагниченность имеют вид:
Здесь: Hi - внутреннее постоянное поле; ![]() .
.
Подставляя (4) и (5) в (1) и (2) и учитывая, что ![]() , а также
, а также ![]() (так как Hi = const, M0 = const), получаем:
(так как Hi = const, M0 = const), получаем:
Из уравнения (6) следует возможность введения потенциала переменного поля ψ такого, что:
При этом уравнение (7) принимает вид:
Это уравнение является основным уравнением для потенциала в среде с намагниченностью. В него входит переменная намагниченность ![]() , которая определяется из уравнения движения вектора намагниченности (Ландау-Лифшица) через переменное поле
, которая определяется из уравнения движения вектора намагниченности (Ландау-Лифшица) через переменное поле ![]() с помощью тензора восприимчивости
с помощью тензора восприимчивости ![]() . Компоненты переменного поля выражаются через потенциал ψ в соответствии с (8). Таким путем компоненты переменной намагниченности
. Компоненты переменного поля выражаются через потенциал ψ в соответствии с (8). Таким путем компоненты переменной намагниченности ![]() можно выразить через потенциал ψ, после чего подставить полученные выражения в (9). При этом получим уравнение для потенциала ψ в чистом виде. Это уравнение Уокера, вид которого определяется явным видом тензора восприимчивости
можно выразить через потенциал ψ, после чего подставить полученные выражения в (9). При этом получим уравнение для потенциала ψ в чистом виде. Это уравнение Уокера, вид которого определяется явным видом тензора восприимчивости ![]() [4].
[4].
Выведем уравнение Уокера для однородной изотропной среды, в которой внутреннее поле равно Hi.
Уравнение движения вектора намагниченности (Ландау-Лифшица) имеет вид:
Здесь γ > 0, при этом свободная прецессия является правой.
В декартовой системе координат векторное произведение имеет вид:
Так как постоянное поле направлено вдоль оси (4), а в дальнейшем предполагается линеаризация, то можно считать, что переменное поле по этой оси отсутствует и ограничиться компонентами переменной намагниченности только по осям Ox и Oy:
Подставляя и в виде (4) и (5), а также выполняя линеаризацию, получаем систему уравнений для mx и my:

Решая эту систему, находим:
Введем обозначения:
При этих обозначениях получаем:
Подставляя в (25) и (26) в (17) и (18), получаем:
Подставляя в (27) и (28) hx и hy в соответствии с (8), получаем:
Подставляя (29) и (30) в (10) и вводя обозначение:
получаем уравнение для потенциала внутри среды - уравнение Уокера в виде:
При этом уравнение для потенциала вне среды при принимает вид уравнения Лапласа:
Граничные условия
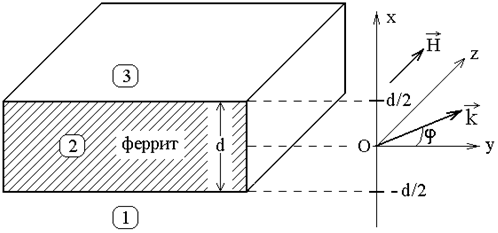
Рассмотрим геометрию задачи:
Рис. 2 - Геометрия задачи
Структура представляет собой безграничную ферритовую пластину 2 толщиной d, по обе стороны от которой находятся пустые полупространства 1 и 3. Система координат Oxyz выбрана таким образом, что ее плоскость Oyz параллельна плоскостям ферритовой пластины, а ось Ox - перпендикулярна. При этом ось Oz ориентирована вдоль направления внешнего поля. Начало координат O находится посередине между поверхностными плоскостями пластины, координаты которых равны ![]() .
.
Граничные условия на поверхностях пластины - непрерывность нормальной компоненты индукции ![]() и тангенциальной компоненты поля
и тангенциальной компоненты поля ![]() :
:
Вычисляя отдельные компоненты ![]() и
и ![]() , получаем:
, получаем:
Граничные условия принимают вид (всего 4 граничных условия):
Вторая пара граничных условий получена из равенства производных, то есть выполняется с точностью до произвольной постоянной, прибавляемой к потенциалу (что является результатом интегрирования). В работе Дэймона-Эшбаха эта постоянная полагается равной нулю, так как все поля вычисляются через производные от потенциала, а производная от постоянной величины равняется нулю.
Полная формулировка задачи
Таким образом, получаем полную задачу в виде:
область 1 (вне феррита):
область 2 (внутри феррита):
область 3 (вне феррита):
Граничные условия на нижней ![]() и верхней
и верхней ![]() поверхностях:
поверхностях:
Решение уравнений без граничных условий
Рассмотрим решение в областях 1 - 3 по отдельности.
Область 1 (вне феррита).
Уравнение для потенциала ψ1 в этой области имеет вид (44):
Решим уравнение (51) методом разделения переменных. Для этого предположим, что решение имеет вид:
Подставим решение (52) в уравнение (51) и разделим все на X1·Y1·Z1. Введем далее постоянные разделения λ1 и µ1. Здесь и далее никаких предположений о действительности или мнимости этих постоянных не делается, знаки и квадраты используются для удобства.
Подставляя (52) в (51), получаем:
Введем постоянную разделения λ1:
Из (54) получаем уравнение для Z1:
Его решение имеет вид:
Здесь и далее буквами A, B, C, D, G, H с соответствующими индексами будем обозначать произвольные постоянные, которые далее будут определены из граничных условий.
Аналогично находим Y1 и X1. Из (54) получаем:
Вводя еще одну постоянную разделения µ1, получаем:
![]()
Из (58) получаем уравнение для X1:
Его решение имеет вид:
Аналогично из (58) получаем уравнение для Y1:
Его решение имеет вид:
Область 2 (внутри феррита).
Уравнение для потенциала ψ1 в этой области имеет вид (45):
Решим уравнение (63) методом разделения переменных. Для этого предположим, что решение имеет вид:
Подставим решение (64) в уравнение (63) и разделим все на X2·Y2·Z2. Введем далее постоянные разделения λ2 и µ2. Здесь также никаких предположений о действительности или мнимости этих постоянных не делается, знаки и квадраты используются для удобства.
Подставляя (64) в (63), получаем:
Введем постоянную разделения λ2:
Из (66) получаем уравнение для Z2:
Его решение имеет вид:
Аналогично находим Y2 и X2. Из (66) получаем:
Вводя еще одну постоянную разделения µ2, получаем:
Из (70) получаем уравнение для X2:
Его решение имеет вид:
Аналогично из (70) получаем уравнение для Y2:
Его решение имеет вид:
Область 3 (вне феррита).
Решение в этой области полностью аналогично решению в области 1 с заменой индекса "1" на индекс "3".
Полное решение имеет вид (формулы (58), (60), (62), (68), (72), (74)):
Предположим, что волна распространяется в плоскости Oyz. При этом зависимости всех трех решений от y и z должны совпадать. Из этого условия получаем:
Введем обозначения µ0 и λ0 из условий:
Подставляя эти обозначения в (84), получаем:
Выражение (88) можно рассматривать как систему двух уравнений относительно µ1 и µ3. Возводя все три составляющих (88) в квадрат, после чего приравнивая первое и третье, а затем первое и второе, получаем:
Так как (согласно сделанному предположению) волна распространяется в плоскости Oyz, то Y1,2,3 и Z1,2,3 являются периодическими. При этом, поскольку они выражаются через экспоненту с мнимой единицей i в показателе, то λ0 и ![]() должны быть действительными.
должны быть действительными.
Предположим, что решение в области 1 спадает до нуля при x → -∞, а в области 3 – при x → +∞. При этом, учитывая, что µ1 > 0 и µ3 > 0, получаем: B1 = 0 и A3 = 0.
Для удобства введем обозначения без индексов: A1 = A и B3 = B, а также: C1,2,3 = C, D1,2,3 = D, G1,2,3 = G, H1,2,3 = H.
В результате полное решение принимает вид:
часть решения, зависящая только от x:
часть решения, зависящая только от y и z, одинаковая во всех областях:
В этом решении 8 постоянных коэффициентов, а граничных условий, по которым их предстоит определять, только 4. Поэтому 4 коэффициента можно задать произвольно. Предположим далее, что волны распространяются только в положительных направлениях осей Oy и Oz, то есть C = 0 и G = 0. Поскольку можно произвольно задать еще два коэффициента, то можно положить D = 1 и H = 1. При этом часть решения, зависящая только от y и z, принимает вид:
Таким образом, в полном решении остаются только 4 коэффициента A, A2, B2, B, для определения которых имеются 4 граничных условия (42), (43).
Введем теперь в решение волновые числа в явном виде с помощью обозначений:
волновое число по координате x вне пластины:
волновое число по координате x внутри пластины:
волновое число по координате y во всем пространстве:
волновое число по координате z во всем пространстве:
Данная система выражений содержит 6 величин: ![]() . Так как четыре уравнения (98)-(101) содержат шесть неизвестных, то две из них можно исключить, в результате чего получатся два уравнения с четырьмя неизвестными. Исключим µ0 и λ0. Для этого выразим их через
. Так как четыре уравнения (98)-(101) содержат шесть неизвестных, то две из них можно исключить, в результате чего получатся два уравнения с четырьмя неизвестными. Исключим µ0 и λ0. Для этого выразим их через ![]() и
и ![]() с помощью (99) и (101), подставим полученные выражения в (98) и (100), откуда после возведения в квадрат, получим:
с помощью (99) и (101), подставим полученные выражения в (98) и (100), откуда после возведения в квадрат, получим:
В эти выражения µ0 и λ0 уже не входят. Однако здесь имеется четыре волновых числа ![]() связанные двумя уравнениями. Поэтому два из них можно задать изначально, а два других выразить через них. Поскольку в плоскости Oyz никаких ограничений для распространения волн нет (геометрически пластина ограничена только по оси Ox), то будем считать заданными ky и kz, а
связанные двумя уравнениями. Поэтому два из них можно задать изначально, а два других выразить через них. Поскольку в плоскости Oyz никаких ограничений для распространения волн нет (геометрически пластина ограничена только по оси Ox), то будем считать заданными ky и kz, а ![]() и
и ![]() выразим через них. Для этого проделаем следующее. Вычитая (103) из (102), получаем:
выразим через них. Для этого проделаем следующее. Вычитая (103) из (102), получаем:
Находя из этого выражения ![]() и подставляя в (102), получаем:
и подставляя в (102), получаем:
Из (104) и (105) после несложных преобразований получаем:
Полное решение в обозначениях (98)-(101) принимает вид:
часть решения, зависящая только от x:
часть решения, зависящая только от y и z, принимает вид:
Здесь ky и kz - пока произвольные действительные величины (их действительность обусловлена отсутствием затухания). При этом из (106) следует, что ![]() тоже всегда действительное, то есть X1 и X3 вне пластины экспоненциально спадают. В то же время, из (107) следует, что
тоже всегда действительное, то есть X1 и X3 вне пластины экспоненциально спадают. В то же время, из (107) следует, что ![]() может быть как действительным, так и мнимым, в зависимости от знака подкоренного выражения, которое определяется соотношением между величинами ky и kz, а также величиной и знаком μ в зависимости от Ω.
может быть как действительным, так и мнимым, в зависимости от знака подкоренного выражения, которое определяется соотношением между величинами ky и kz, а также величиной и знаком μ в зависимости от Ω.
Частотные области объемных и поверхностных волн
Найдем частотные области объемных и поверхностных волн, для чего рассмотрим зависимость μ(Ω), определяемую формулой (31):
Возможны следующие случаи:
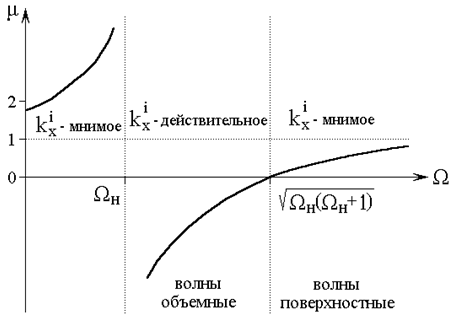
Схема зависимости μ(Ω) приведена на рис. 3.
Рис. 3 - Схема зависимости μ от Ω.
Имеется только одна область 3: ![]() , где μ < 0, то есть может быть действительным. Это - область объемных волн, для которых зависимость потенциала ψ2 от координаты x периодически осциллирует. В этой области действительность
, где μ < 0, то есть может быть действительным. Это - область объемных волн, для которых зависимость потенциала ψ2 от координаты x периодически осциллирует. В этой области действительность ![]() определяется соотношением между ky и kz, определяемым условием:
определяется соотношением между ky и kz, определяемым условием:
откуда получаем:
что дает сектор, определяющий возможные пределы распространения объемных волн. Его величину удобно определять в цилиндрической системе координат с помощью угла отсечки.
В области 2: 0 < Ω < ΩH, где μ > 0, волны не распространяются, так как при этом их частота должна была бы быть ниже частоты однородного ФМР.
В области 5: ![]() , где μ > 0, величина
, где μ > 0, величина ![]() всегда мнимая. Это область поверхностных волн, для которых зависимость потенциала ψ2 от координаты x спадает по экспоненте от той или иной поверхности пластины.
всегда мнимая. Это область поверхностных волн, для которых зависимость потенциала ψ2 от координаты x спадает по экспоненте от той или иной поверхности пластины.
Вывод дисперсионного отношения из решения и граничных условий
Решение имеет вид:
Граничные условия на нижней ![]() и верхней
и верхней ![]() поверхностях имеют вид (47)-(50):
поверхностях имеют вид (47)-(50):
Подставим решение (121)-(123) в граничные условия (124)-(127) и разделим первые два уравнения на Z, а вторые два уравнения на YZ. При этом получим граничные условия в виде:
Здесь согласно (108)-(112):
Находим производные из решения (132)-(135):
Введем обозначения:
Производные и решение на границах принимают вид:
Подставляя (135), (139), (142)-(149) в граничные условия (128)-(131) и разделяя на ![]() , получаем систему уравнений для A, A2, B2, B:
, получаем систему уравнений для A, A2, B2, B:
Введем обозначения:
С этими обозначениями из (150)-(153) получаем:
Это - система 4 уравнений с 4 неизвестными A, A2, B2, B. Условием существования ненулевого решения является равенство нулю ее определителя: D0 = 0, что и дает дисперсионное соотношение. Этот определитель имеет вид:
Для раскрытия этого определителя умножим третью строку на ![]() и прибавим к первой, а затем умножим четвертую строку на
и прибавим к первой, а затем умножим четвертую строку на ![]() и прибавим ко второй. В результате получаем:
и прибавим ко второй. В результате получаем:
Этот определитель разлагаем по четвертому столбцу, а тот, который остается - по третьему. Учитывая далее, что должно быть D0 = 0, получаем уравнение вида:
Раскрывая входящий в (162) определитель, получаем:
откуда получаем дисперсионное соотношение в виде:
Здесь входящие в (164) величины определяются через волновые числа в соответствии с формулами (продублированы для справки):
В дисперсионное соотношение (164) входят четыре волновых числа: ![]() ky, kz. Два из них
ky, kz. Два из них ![]() и
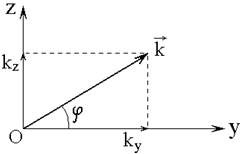
и ![]() с помощью выражений (168) и (169) можно исключить. При этом в дисперсионное соотношение будут входить только ky и kz. Это означает, что если задано, например ky, то дисперсионное соотношение позволяет определить через ky. Такое исключение можно удобно сделать в полярной системе координат, показанной на рис.3.
с помощью выражений (168) и (169) можно исключить. При этом в дисперсионное соотношение будут входить только ky и kz. Это означает, что если задано, например ky, то дисперсионное соотношение позволяет определить через ky. Такое исключение можно удобно сделать в полярной системе координат, показанной на рис.3.
Рис.3 - Волновой вектор в полярной системе координат.
При этом:
В этой системе координат волновые числа (168) и (169) принимают вид:
где введено обозначение:
Вычислим промежуточные выражения, входящие в дисперсионное соотношение (164):
где введено обозначение:
При этом получаем:
Подставляя (175), (179) и (180) в (164), получаем:
откуда получаем:
или:
Преобразуя (183) получаем основное дисперсионное соотношение для изотропной ферритовой пластины со свободными поверхностями, намагниченной в плоскости:
Здесь в соответствии с (174), (178), (31), (21), (22), (24):
Дисперсионное соотношение (184) можно разрешить относительно k. Для этого удобно воспользоваться выражением (182), а именно: умножить числитель и знаменатель его правой части на ekdα, после чего разрешить полученное уравнение относительно e2kdα, откуда выразить k с помощью логарифма. В результате получаем дисперсионное соотношение в виде:
Построение графика зависимости
Для вывода уравнения дисперсионной зависимости ω(k) была выбрана формула дисперсионного соотношения (190). В результате преобразований и с учетом того, что для ПОМСВ волновой вектор k перпендикулярен внешнему магнитному полю, было получено следующее уравнение:
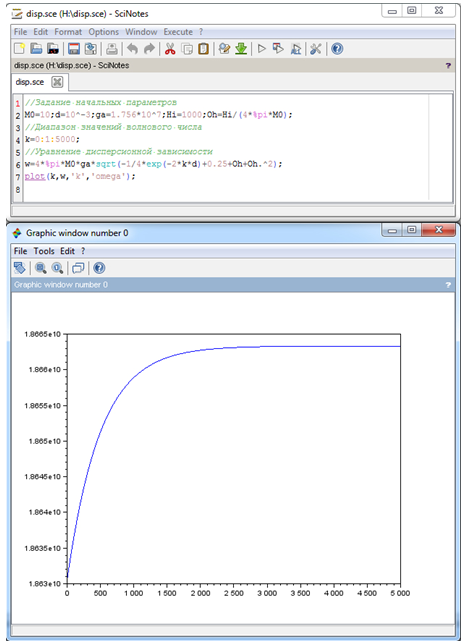
Далее для расчета полученной зависимости в пакете Scilab [5] был написан программный код, а также построен график зависимости. Они изображены на рисунке 4. В данном примере расчет производился в диапазоне волновых чисел от единицы до 5000, величина намагниченности M0 равняется 10 Гс, индукция внешнего поля Hi равна 1000 Э, толщина пленки d равна 10 мкм.
Рис. 4 - Окна программы Scilab с программным кодом и графиком дисперсионной зависимости.
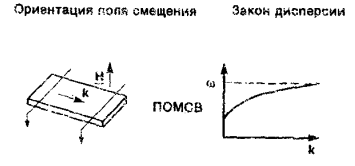
Из графика видно, что полученная зависимость достаточно хорошо коррелирует с законом дисперсии для ПОМСВ, представленным на рисунке 5, то есть, чем больше волновое число, тем выше частота, которая в определенный момент уходит в насыщение и больше не растет.
Рис. 5 - Закон дисперсии для ПОМСВ [6].
Сравнение зависимостей при различных параметрах
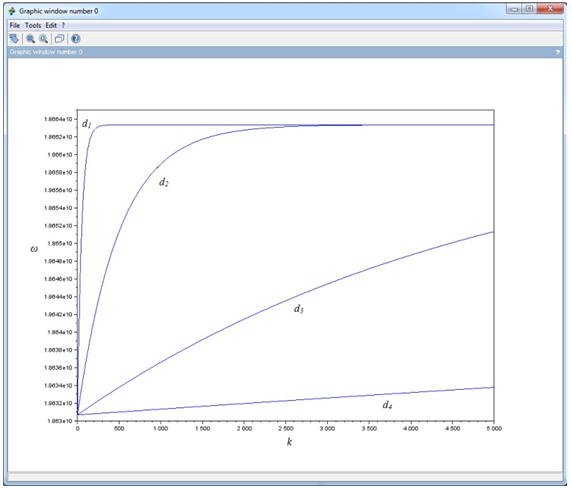
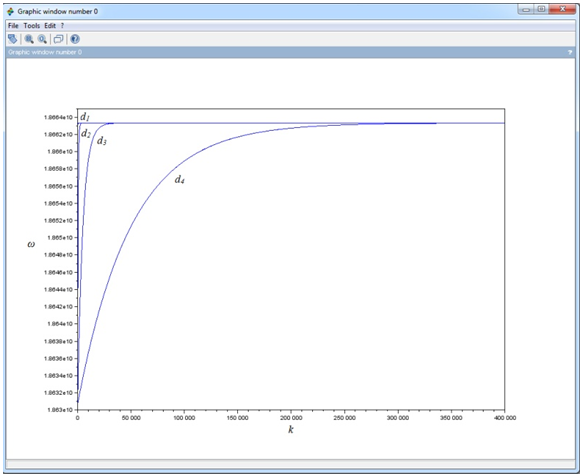
Далее на одном графике было построено несколько зависимостей ω(k) для разных значений толщины пленки d. График изображен на рисунке 6. На втором графике изображены те же зависимости для k от 1 до 400000. Намагниченность и поле те же, что и в предыдущем примере.
Рис. 6 - Дисперсионная зависимость ПОМСВ для пленок с различной толщиной (d1 = 0,1 мкм, d2 = 1 мкм, d3 = 10 мкм, d4 = 100 мкм).
Видно, что чем пленка тоньше, тем более пологая в итоге получается зависимость, то есть для тонких пленок частота растет гораздо быстрее, чем для более толстых. При этом на масштабе k 1÷400000 становится заметно, что все зависимости перестают расти, достигнув частоты примерно 18,663 МГц (тем быстрее, чем толщина пленки меньше).
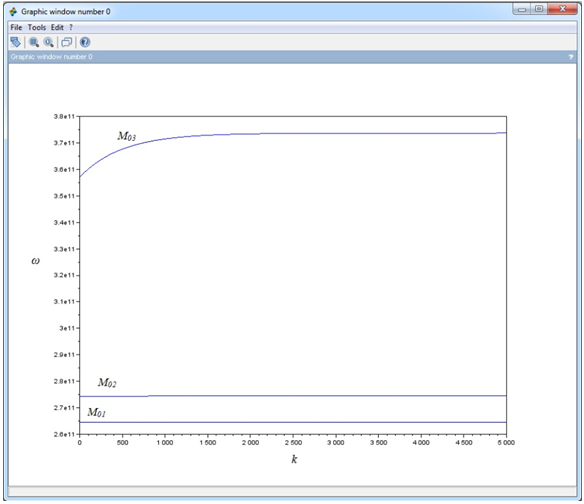
Также на одном графике было построено несколько зависимостей ω(k) для разных значений намагниченности пленки M0 при одном и том же значении Hi. График изображен на рисунке 7.
Рис. 7 - Дисперсионная зависимость ПОМСВ при разной величине намагниченности (M01 = 10 Гс, M02 = 100 Гс, M03 = 1000 Гс, Hi = 15000 Э, d = 10 мкм).
Из графика видно, что с ростом намагниченности при фиксированном поле также растет и частота, причем для больших M0 частота растет сильнее (верхняя кривая на рисунке 7). Кроме того, чем меньше намагниченность, тем быстрее частота прекращает свой рост (две нижние прямые на рисунке 7).
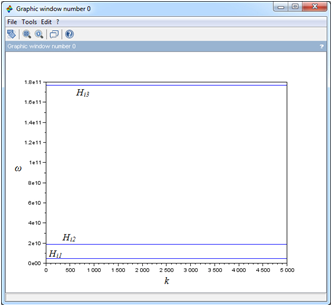
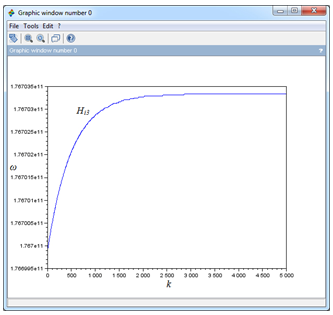
Далее на одном графике было построено несколько зависимостей ω(k) для разных значений величины поля Hi при одном и том же значении намагниченности пленки M01. Кроме того, так как данный масштаб не позволяет увидеть форму каждой зависимости, были построены отдельные графики для каждого значения Hi Графики изображены на рисунке 8.
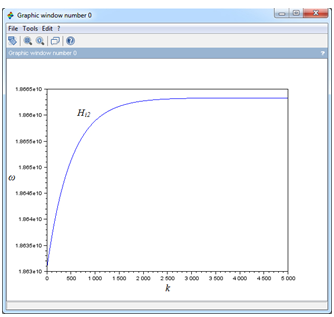
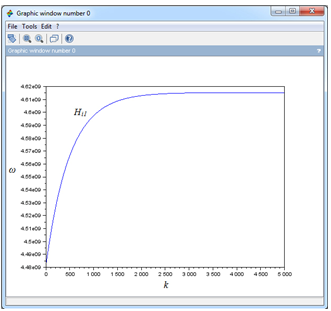
Рис. 8 - Дисперсионная зависимость ПОМСВ при разной величине намагниченности пленки (Hi1 = 200 Э, Hi2 = 1000 Э, Hi3 = 10000 Э, M0 = 10 Гс, d = 10 мкм).
Из графиков видно, что с ростом поля при фиксированной намагниченности также растет и частота, причем для больших Hi частота растет гораздо медленнее, но чем выше Hi, тем выше лежит сама зависимость (частота для верхней прямой на первом изображении рисунка 8 на порядок отличается от частоты для средней прямой).
Заключение
В ходе данной работы был произведен расчет дисперсионных характеристик магнитостатических волн. Были поставлены следующие задачи:
- вывод дисперсионного соотношения для объемных магнитостатических волн;
- получение дисперсионной зависимости ω(k);
- написание программы для численного расчета зависимости при разных значениях поля и толщины пленки в пакете Scilab, построение сравнительных графиков.
Все поставленные задачи были выполнены. Было построено несколько зависимостей для различных параметров, таких как толщина пленки величина внешнего поля и намагниченность пленки. Все полученные результаты соответствуют закону дисперсии для объемных магнитостатических волн, и все зависимости независимо от параметров имеют одинаковую форму (каждая на своем масштабе). Было найдено, что при разной толщине пленки частоты остаются неизменными, при этом для тонких пленок зависимость растет быстрее. Также для больших полей и намагниченности зависимости лежат выше.
Все характеристики рассчитывались для объемных магнитостатических волн.
Литература
- Гуляев Ю. В., Зильберман П. Е. Взаимодействие СВЧ спиновых волн и электронов в слоистых структурах полупроводник-феррит (обзор) // РиЭ. – 1978. – Т. 23, № 5. C. 897.
- Адам Дж. Д., Коллинз Дж. Х. Магнитостатические линии задержки сантиметрового диапазона на основе эпитаксиальных пленок железоиттриевого граната // ТИИЭР. – 1976. – Т. 64, №5. C. 277-285.
- Данилов В. В., Зависляк И. В., Балинский М. Г. Спинволновая электродинамика. Киев: Либщь, 1991. 212 с.
- Джексон Дж. Д. Классическая электродинамика. Пер. с англ. Г. В. Воскресенского и Л. С. Соловьева. Под ред. Э. Л. Бурштейна. М.: Мир, 1965. 703 с.
- Scilab [Электронный ресурс] URL: http://www.scilab.org (дата обращения 17.12.2014).
- Исхак В. С. Применение магнитостатических волн (обзор) // ТИИЭР. – 1988. – Т. 76, №2. C. 86-104.
References
- Guljaev Ju. V., Zil'berman P. E. Vzaimodejstvie SVCh spinovyh voln i jelektronov v sloistyh strukturah poluprovodnik-ferrit (obzor) // RiJe. – 1978. – T. 23, № 5. S. 897.
- Adam J. D., Collins J. H. Magnitostaticheskie linii zaderzhki santimetrovogo diapazona na osnove jepitaksial'nyh plenok zhelezoittrievogo granata // TIIJeR. – 1976. – T. 64, №5. S. 277-285.
- Danilov V. V., Zavisljak I. V., Balinskij M. G. Spinvolnovaja jelektrodinamika. Kiev: Libshh', 1991. 212 s.
- Jackson J. D. Klassicheskaja jelektrodinamika. Per. s angl. G. V. Voskresenskogo i L. S. Solov'eva. Pod red. Je. L. Burshtejna.: M.: Mir, 1965. 703 s.
- Scilab [Jelektronnyj resurs] URL: http://www.scilab.org (data obrashhenija 17.12.2014).
- Ishak V. S. Primenenie magnitostaticheskih voln (obzor) // TIIJeR. – 1988. – T. 76, №2. C. 86-104.