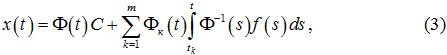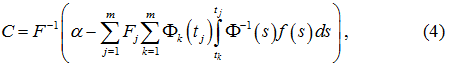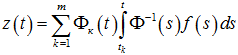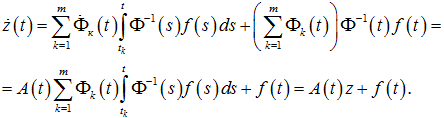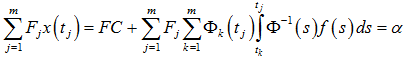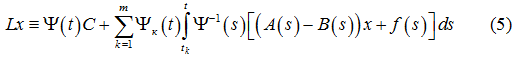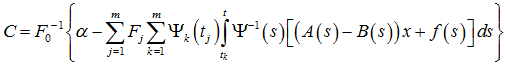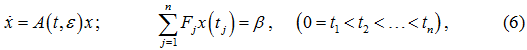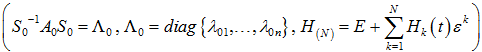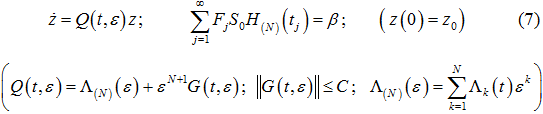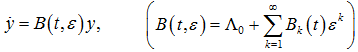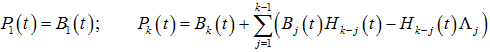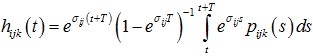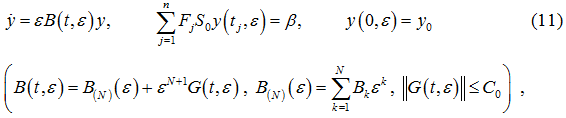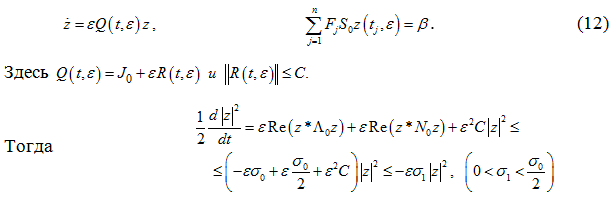SPLITTING METHOD OF THE STUDY OF MULTIPOINT BOUNDARY VALUE PROBLEMS ON THE HALF-LINE
Коняев Ю.А.1, Кленина Л.И.2
1доктор физико-математических наук, доцент, 2кандидат физико-математических наук, доктор педагогических наук, доцент, Национальный исследовательский университет «Московский энергетический институт»
МЕТОД РАСЩЕПЛЕНИЯ ИССЛЕДОВАНИЯ МНОГОТОЧЕЧНЫХ КРАЕВЫХ ЗАДАЧ НА ПОЛУОСИ
Аннотация
Изучены вопросы существования и единственности решения краевых задач для неавтономных однородных систем обыкновенных дифференциальных уравнений с T – периодической матрицей при наличии регулярных возмущений. Получены достаточные условия устойчивости и асимптотической устойчивости решений таких задач.
Ключевые слова: системы с T - периодической матрицей, регулярные возмущения, устойчивость, асимптотика.
Konyaev Yu.A.1, Klenina L.I.2
1PhD in Physics and mathematics, professor, 2PhD in Physics and mathematics, PhD of pedagogical Sciences, professor, National research University «Moscow power engineering Institute»
SPLITTING METHOD OF THE STUDY OF MULTIPOINT BOUNDARY VALUE PROBLEMS ON THE HALF-LINE
Abstract
Studied the existence and uniqueness of the solution of boundary value problems for non-Autonomous homogeneous systems of ordinary differential equations with T – periodic matrix in the presence of a regular perturbation. We obtained sufficient conditions of stability and asymptotic stability of solutions of such problems.
Keywords: the systems with T - periodic matrix, the regular perturbations, the stability, the asymptotics.
- Существование и единственность решения краевой задачи на полуоси
Рассмотрим линейную систему
где Fj – некоторые постоянные матрицы, j=1,2,…,m.
При значении m=1 получаем известную начальную задачу, решение которой всегда существует и единственно. При 2 ≤ m ≤ n решение краевой задачи (1)–(2) не всегда существует.
При анализе многоточечных начально краевых задач вида (1)–(2) на полуоси следует выделить два момента.
- Существование единственного решения на любом конечном отрезке [0,t0] ⊂ R+, (t0>1)
- В случае существования такого решения на полуоси необходимо исследовать его на устойчивость (или асимптотическую устойчивость) при t→+∞.
Сформулируем [1] теорему об однозначной разрешимости и укажем конкретный алгоритм построения решения задачи (1)–(2) без использования традиционного аппарата функции Грина.
Теорема 1. Если для задачи (1)–(2) выполняется условие detF≠0, где ![]() , а Φ(t) – произвольная фундаментальная матрица соответствующей однородной (f (t) ≡ 0) системы (1), тогда краевая задача (1)–(2) однозначно разрешима на любом [0,t0] (t0≥1) и её решение может быть представлено в виде
, а Φ(t) – произвольная фундаментальная матрица соответствующей однородной (f (t) ≡ 0) системы (1), тогда краевая задача (1)–(2) однозначно разрешима на любом [0,t0] (t0≥1) и её решение может быть представлено в виде
где
Φk(t) – квадратные матрицы (k = 1,2,…,n), содержащие столбцы фундаментальной матрицы Φ(t) и при этом
Доказательство. Справедливость представления (3) следует из того, что оно является суммой общего решения Φ(t)C однородного уравнения и частного решения неоднородного уравнения (1) специального вида
Это проверяется прямым дифференцированием последнего равенства.
В самом деле,
При этом вектор C однозначно определяется краевыми условиями
что и завершает доказательство теоремы 1.
Замечание 1. Теорема 1 является эффективной, т.е. решение явно выписывается формулой (3) только при известной фундаментальной матрице Φ(t). В общем случае следует построить близкую к системе (1) другую систему ẋ=B(t)x, где разность A(t) – B(t) на отрезке [0,t0] достаточно мала по некоторой норме. Тогда, если выполняется условие detF0≠0, где ![]() , и Ψ(t)– произвольная фундаментальная матрица системы ẋ=B(t)x, то решение задачи (1)–(2) может быть сведено к решению эквивалентного специального интегрального уравнения x=Lx, здесь
, и Ψ(t)– произвольная фундаментальная матрица системы ẋ=B(t)x, то решение задачи (1)–(2) может быть сведено к решению эквивалентного специального интегрального уравнения x=Lx, здесь
и вектор C определяется по аналогии с формулой (4) как
Оператор L, введённый в формуле (5), при достаточной малости нормы ||A(t) – B(t)||, будет сжимающим, что гарантирует однозначную разрешимость интегрального уравнения x=Lx и эквивалентной ему начально краевой задаче (1)–(2).
- Анализ краевых задач на полуоси для однородных систем с T - периодической матрицей при наличии регулярных возмущений
Рассмотрим краевые задачи для однородных систем с T – периодической матрицей A(t), представимой в виде A(t) = A0+δA(t) где 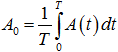 – среднее значение, а δ – некоторый параметр.
– среднее значение, а δ – некоторый параметр.
Следуя методу расщепления [2, с.13] для произвольной квадратной n×n матрицы ![]() , введём обозначения для её «диагональной» части
, введём обозначения для её «диагональной» части ![]() и «бездиагональной» части
и «бездиагональной» части ![]() .
.
Теорема 2. Пусть дана однозначно разрешимая краевая задача с T – периодической матрицей:
где матричный ряд ![]() из T – периодических матриц Ak(t) сходится абсолютно и равномерно по некоторой норме при достаточно малых |ε|<1 и t ≥ 0.
из T – периодических матриц Ak(t) сходится абсолютно и равномерно по некоторой норме при достаточно малых |ε|<1 и t ≥ 0.
Если матрица A0 имеет простой спектр ![]() удовлетворяющий условиям
удовлетворяющий условиям ![]() , тогда задача (6) при достаточно малых |ε|<1 с помощью невырожденной T – периодической замены
, тогда задача (6) при достаточно малых |ε|<1 с помощью невырожденной T – периодической замены ![]() ;
;
может быть приведена к краевой задаче с почти диагональной матрицей вида
где постоянные диагональные матрицы Λk и T – периодические матрицы Hk(t) однозначно определяются с помощью итерационного алгоритма (k = 1,2,…,N).
Доказательство. В условиях теоремы всегда существует невырожденная замена x=S0y, приводящая систему (6) к виду
Последующее преобразование y=H(N)(t,ε)z, невырожденное при |ε|<1, даёт нужный результат (7), если матрицы B(t,ε), H(N)(t,ε) и Q(t,ε) удовлетворяют дифференциальному матричному уравнению
Приравнивая в последнем уравнении коэффициенты при одинаковых степенях ε, получим однотипные дифференциальные матричные уравнения вида
Разбив уравнение (8) на «диагональную» и «бездиагональную» части, получим два уравнения
Первое из этих уравнений имеет единственное T – периодическое решение 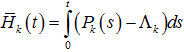 , если
, если 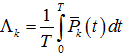 (k=1,2,…,N).
(k=1,2,…,N).
Второе матричное уравнение распадается на (n2 – n) скалярных дифференциальных уравнений вида: ![]() (i, j=1,2,…,n; i≠j; k=1,2,…,N), имеющих в условиях теоремы 2 единственное T – периодическое решение
(i, j=1,2,…,n; i≠j; k=1,2,…,N), имеющих в условиях теоремы 2 единственное T – периодическое решение
Оценка ||G(t,ε)||≤C проверяется непосредственно. Теорема 2 доказана.
- Анализ устойчивости решений
Теорема 3. Если в условиях теоремы 2 спектр ![]() матрицы Λ(N)(ε) в задаче (7) удовлетворяет неравенствам
матрицы Λ(N)(ε) в задаче (7) удовлетворяет неравенствам ![]() (j=1,2,…,n; q=0,1,2,…,N), тогда решение задачи (7) на полуоси и эквивалентной ей задаче (6) асимптотически устойчиво.
(j=1,2,…,n; q=0,1,2,…,N), тогда решение задачи (7) на полуоси и эквивалентной ей задаче (6) асимптотически устойчиво.
Доказательство. Применяя дифференциальное неравенство для квадрата нормы решения задачи [2, с.14] получаем оценку ![]() , из которой следует асимптотическая устойчивость решения задачи (6), что и требовалось доказать.
, из которой следует асимптотическая устойчивость решения задачи (6), что и требовалось доказать.
Теорема 4. Пусть выполнены условия теоремы 2. Если спектр ![]() матрицы Λ(N)(ε) в задаче (7) удовлетворяет неравенствам
матрицы Λ(N)(ε) в задаче (7) удовлетворяет неравенствам ![]() (j=1,2,…,n), то асимптотика (ε→+0) решения краевой задачи (6) с Т – периодической матрицей может быть представлена в виде:
(j=1,2,…,n), то асимптотика (ε→+0) решения краевой задачи (6) с Т – периодической матрицей может быть представлена в виде: ![]() , где вектор C однозначно определяется из краевых условий
, где вектор C однозначно определяется из краевых условий ![]() , а матричные функции Λ(N)(ε) и H(N)(tj,ε) однозначно определяются методами теоремы 2.
, а матричные функции Λ(N)(ε) и H(N)(tj,ε) однозначно определяются методами теоремы 2.
Доказательство. Применяя дифференциальное неравенство Бернулли [2, с.15]: ![]() , а вектор функция p(t,ε) удовлетворяет вспомогательной задаче
, а вектор функция p(t,ε) удовлетворяет вспомогательной задаче ![]() , получаем оценку
, получаем оценку 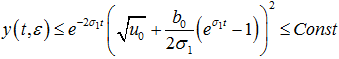 , которая завершает доказательство теоремы 4 [2, с.15].
, которая завершает доказательство теоремы 4 [2, с.15].
Замечание 2. Теорема 2 является аналогом метода усреднения для заданного класса задач.
- Анализ периодических систем в критических случаях
Рассмотрим систему:
(где матричный ряд ![]() из непрерывных T– периодических матриц Ak(t), (k=0,1,2,…), сходится абсолютно и равномерно при |ε|<<1 и t ≥ 0).
из непрерывных T– периодических матриц Ak(t), (k=0,1,2,…), сходится абсолютно и равномерно при |ε|<<1 и t ≥ 0).
Теорема 5. Для однозначно разрешимой краевой задачи (9) при наличии T – периодической матрицы A0(t) произвольной жордановой структуры при |ε|<<1 существует невырожденная Т – периодическая замена
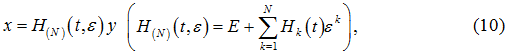
приводящая задачу (9) к эквивалентной задаче с почти постоянной матрицей вида
причем матрицы Bk и Hk(t) однозначно определяются с помощью итерационного алгоритма (k=0,1,2,…,N).
Доказательство. Прямая подстановка (10) в (9) даёт нужный результат (11), если матрицы A(t,ε), H(N)(t,ε) и B(t,ε) удовлетворяют дифференциальному матричному уравнению
Приравнивая в последнем уравнении коэффициенты при одинаковых степенях ε, получим набор однотипных дифференциальных матричных уравнений вида ![]() ,
,
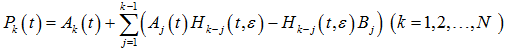 , которые имеют единственное Т – периодическое решение при каждом k=1,…,N. В этом случае
, которые имеют единственное Т – периодическое решение при каждом k=1,…,N. В этом случае 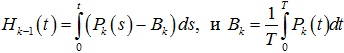 .
.
Оценка ||G(t,ε)||≤C0 проверяется простым вычислением.
Теорема 6. Если в условиях теоремы 5 для однозначно разрешимой краевой задачи (9) спектр ![]() матрицы B0 удовлетворяет условиям
матрицы B0 удовлетворяет условиям ![]() тогда решение задачи (9) и эквивалентной ей задачи (11) будет асимптотически устойчиво.
тогда решение задачи (9) и эквивалентной ей задачи (11) будет асимптотически устойчиво.
Доказательство. Всегда существует невырожденная замена:
С помощью этой замены задача (11) приводится к эквивалентной ей задаче вида
Оценка |z(t,ε)|≤|z0|exp(-εσ1t)→0 при t→+∞, гарантирует асимптотическую устойчивость решений эквивалентных задач (12), (11) и (9), что и требовалось доказать.
Вывод. В данной статье с помощью нетрадиционного подхода (т.е. без использования функции Грина) продемонстрирован метод расщепления для анализа краевых задач на полуоси.
Для систем с T – периодической матрицей получены конструктивные достаточные критерии устойчивости (и асимптотической устойчивости) решений таких задач, что можно рассматривать как обобщение теоремы Ляпунова об асимптотической устойчивости по первому приближению для указанного класса задач.
Литература
- Коняев Ю.А. Асимптотические и аналитические методы решения некоторых классов прикладных модельных задач: Монография. – М.: изд-во Российского университета дружбы народов, – 160 с.
- Коняев Ю.А., Кленина Л.И. О некоторых классах многоточечных краевых задач для - периодических систем на полуоси / Современное состояние естественных и технических наук: Материалы XIX Международной научно-практической конференции (19.06.2015). – М.: Издательство «Спутник +», с. 10-16.
References
- Konyaev Yu. A. Asymptotic and analytical methods for solving some classes applied model problems: Monograph. – M.: publishing house of the Russian University of friendship of peoples, 2005. – 160 p.
- Konyaev Yu. A., Klenina I. On some classes of multipoint boundary value problems for - periodic systems on the half-line / The modern condition of natural and technical Sciences: The materials of the XIX International scientific-practical conference (19.06.2015). – M.: Publishing House "Sputnik +", 2015. p. 10-16.