Scaling relations in one-dimensional Ising systems of finite size
Scaling relations in one-dimensional Ising systems of finite size
Abstract
In this work, the scaling relations in one-dimensional Ising systems of finite size, described by a modified Ising model taking into account interactions in the second and third coordination spheres, are studied. In such systems, phase transitions are implemented only at zero temperature, but their influence is also manifested in the region of finite temperatures. Simulation of relaxation processes at the transition between magnetic phases using the Metropolis algorithm of the Monte Carlo method has been carried out. On the basis of the obtained data, critical phenomena are analysed using the scaling theory, including the verification of the hypothesis of scale invariance and dynamical scaling. It is found that for systems of finite size, deviations from classical scaling relations due to the influence of boundary effects are observed. Nevertheless, the qualitative behaviour of the critical indices indicates the preservation of some features characteristic of critical phenomena.
1. Введение
Одномерные ферро- и антиферромагнитные системы, описываемые моделью Изинга, представляют собой важный класс моделей в физике конденсированного состояния. Эти системы демонстрируют уникальные свойства, не присущие макротелам, например, наличие квантовых фазовых переходов при нулевой температуре. Изучение критических явления и определение критических индексов таких систем, сложная экспериментальная задача ввиду малости размеров и низких температур. Теоретически, фазовые переходы (включая квантовые фазовые переходы) в одномерной модели Изинга реализуются только при нулевой температуре и в бесконечной системе. Однако их влияние на физические свойства вещества проявляется и в области конечных температур
. Для систем конечного размера при варьировании параметров наблюдаются изменения, которые можно интерпретировать как размытые или «смазанные» фазовые переходы, обусловленные конечностью системы и влиянием граничных эффектов.2. Методы и принципы исследования
Базовая модель Изинга, дополненная учетом взаимодействия во второй и третьей координационной сфере, хорошо согласуется с экспериментальными данными и позволяет упростить процесс изучения низкоразмерных магнетиков
. Модифицированный гамильтониан имеет вид:где J1, J2, J3 — энергия обменного взаимодействия спинов в первой, во второй и третьей координационных сферах соответственно, J1-4 — энергия четырехчастичного взаимодействия, H — напряженность внешнего магнитного поля, Si — проекция вектора спина на выбранную ось, N — количество атомов в системе, i — номер узла. В исследовании используется относительная температура T — единицы измерения J1/kБ.
Была проведена симуляция релаксационных процессов при переходе между магнитными фазами с использованием алгоритма Метрополиса метода Монте-Карло. Для различных параметров системы были получены значения энергии, времени релаксации, корреляционной длины, что позволило рассчитать критические индексы низкоразмерного магнетика.
3. Основные результаты
Вблизи нулевой температуры система проявляет критические свойства, которые могут быть описаны с использованием скейлинговой теории , . В этой теории вещество вблизи точки фазового перехода рассматривается как система флуктуирующих областей с характерным размером ∼ ξ. Где ξ — корреляционная длина, характеризующая расстояние, на котором спины коррелируют друг с другом . Гипотеза масштабной инвариантности позволяет вывести универсальные соотношения между критическими показателями, причем только два из них являются независимыми, так называемый двухпараметрический скейлинг . Наиболее популярной является линейная модель уравнения состояния, которая включает лишь две не универсальные константы помимо критических параметров вещества. На аналогичных принципах основана теория, связывающая критические индексы кинетических свойств с индексами термодинамических величин — динамический скейлинг. Он отличается от статического скейлинга, который ограничивается исключительно термодинамическими (равновесными) свойствами материи . Одно из соотношений динамического скейлинга, которое было проверено в данном исследовании, имеет следующий вид :
где Y — кинетический критический индекс, характеризующий зависимость времени релаксации перехода антиферромагнетик-ферромагнетик от температуры, z — динамический критический индекс, характеризующий зависимость времени релаксации от размеров системы, ν — статический критический индекс, который характеризует зависимость корреляционной длины от температуры вблизи критической точки.
Для проверки была выбрана температурная зависимость системы из 11 узлов при нулевом внешнем магнитном поле и взаимодействии, ограниченном второй координационной сферой (рис. 1.а). В одной области были построены две функции: Y(T) и z*ν(T).
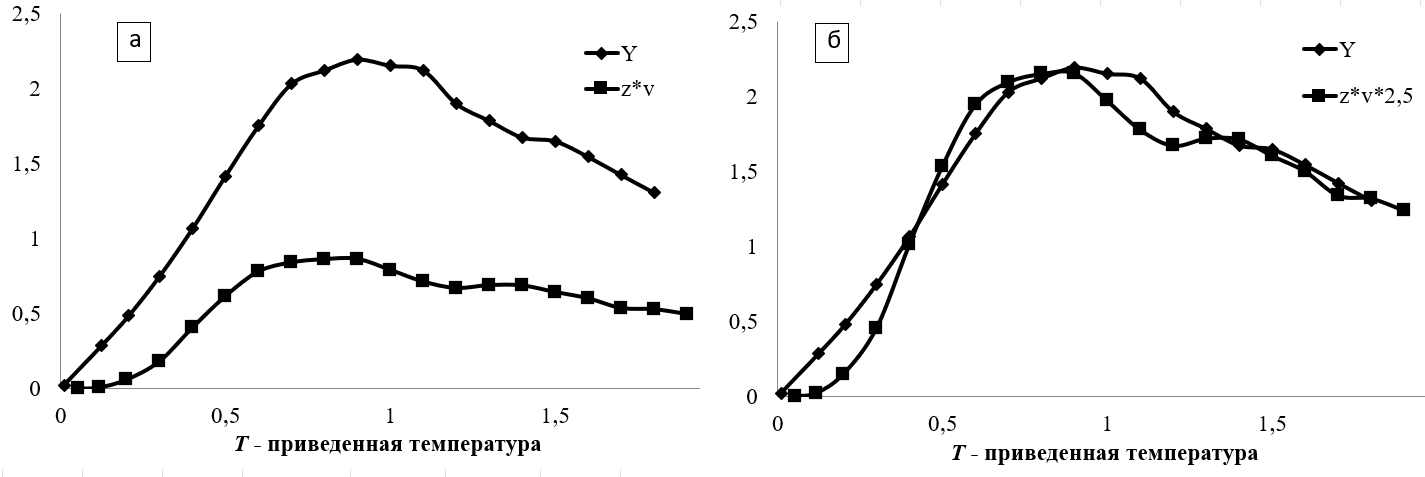
Рисунок 1 - Температурная зависимость индексов Y и z·ν
Примечание: H=0; J2=0,1; N=11; εY~16%, εzν~18%
Гипотеза динамического скейлинга предполагает, что эти функции должны совпадать в критической области. Однако в данном случае наблюдается значительное расхождение между этими функциями (примерно в 2,5 раза — рис 1.б), что выходит за рамки ожидаемого отклонения в 20% (ненулевая температура, конечные размеры). Это указывает на то, что гипотеза динамического скейлинга не выполняется для данной системы в рассматриваемых условиях. Несмотря на количественное расхождение, качественное поведение функций Y(T) и z·ν(T) схоже. Это может свидетельствовать о том, что система демонстрирует некоторые черты, характерные для динамического скейлинга, но с существенными отклонениями, вызванными конечным размером системы или особенностями взаимодействия.
Таким образом, можно заключить, что гипотеза динамического скейлинга неприменима к малым низкоразмерным магнитным системам. Конечный размер системы может вызывать дополнительные эффекты, такие как граничные условия и дискретность спектра, которые нарушают скейлинговые соотношения. Поведение времени релаксации и критических индексов также указывает на особенности свойств таких систем, которые совпадают с теоретическими представлениями (в основном сформулированными для макротел) лишь в отдельных случаях. Однако система сохраняет черты, характерные для критических явлений.
Неравенство
лежащее в основе применимости теории Ландау, может быть переформулировано как условие ξ >> r0, где r0 представляет собой размер области тела, в которой среднеквадратичная флуктуация параметра порядка сравнивается с его характерным равновесным значением. При уменьшении параметра t величина r0 возрастает быстрее, чем корреляционная длина ξ, и на границе области применимости теории Ландау эти величины становятся сравнимыми. Ключевое предположение, лежащее в основе описания флуктуационной области, заключается в отсутствии какого-либо малого параметра в теории. В частности, выполняется условие r0∼ξ, что делает корреляционную длину ξ единственным характерным масштабом, определяющим флуктуации. Данное предположение известно как гипотеза масштабной инвариантность
.Для оценки флуктуаций в объеме V∼ξ3 можно воспользоваться формулой:
Подставив объем V∼ξd и выразив все величины χ, ξ, η через параметр времени согласно определениям критических индексов, получим:
Прологарифмируем уравнение по основанию е и разделим на lnt:
По мере приближения к точке фазового перехода (t→0):
Тогда
которое с учетом равенства (J.W. Essam, M.E. Fisher)
преобразуется в
Проверим данное соотношение для одномерной модели Изинга (d=1). Для проверки выбрана температурная зависимость системы из 10 узлов при нулевом внешнем магнитном поле и взаимодействии ограниченном только первой координационной сферой (рис. 2). В одной области было построено две функции: ν(T) и 2-α(T).
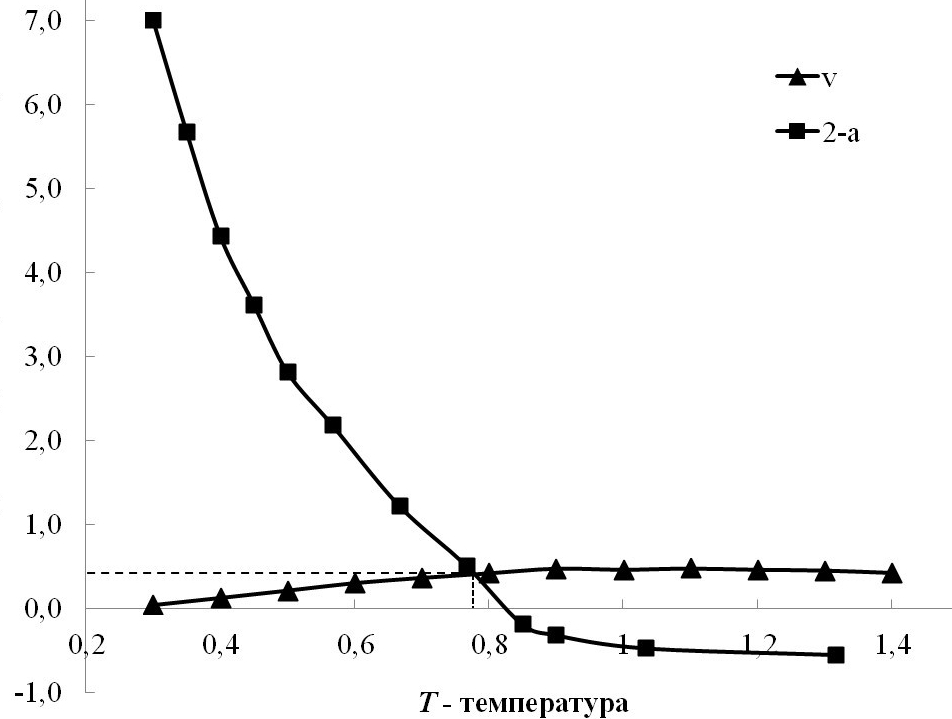
Рисунок 2 - Температурная зависимость индексов ν и 2-α
Примечание: H=J2=J3=0; N=11; εα~13%, εν~8%
4. Заключение
Можно сделать вывод, что гипотеза скейлинга строго применима только вблизи критической точки, где флуктуации становятся масштабно-инвариантными. Вне этой области влияние конечного размера системы и других факторов приводит к отклонениям от скейлинговых соотношений.
Динамический скейлинг является важным инструментом для описания временных корреляций и релаксационных процессов в одномерных магнитных системах. Исследования динамического скейлинга продолжают углублять наше понимание магнитоупорядоченности и критических явлений в низкоразмерных системах.
