A study of adaptive optimal complex finite-time filtering method of navigational arbitrary discrete signals under conditions of parametric a priori uncertainty
A study of adaptive optimal complex finite-time filtering method of navigational arbitrary discrete signals under conditions of parametric a priori uncertainty
Abstract
This work examines a new adaptive finite-time optimal filtering algorithm for arbitrary discrete navigation signals of a two-channel complex system with a difference signal filter under conditions of wide parametric uncertainty, when the distribution laws, first and second moments, correlation functions and mathematical expectations of the errors of the sensors are unknown. In the presented work, the advantages of the finite-time signal filtering method in comparison with Kalman filtering are discussed. The study and comparison of adaptive and non-adaptive finite-time and Kalman methods in terms of accuracy, transient time and robustness under conditions of wide parametric uncertainty is carried out.
1. Введение
В настоящее время алгоритмы фильтрации Калмана имеют широкое распространение при решении задач оптимальной обработки информации, в том числе и при комплексировании навигационных систем на борту летательных аппаратов. Фильтр Калмана обладает рядом достоинств, которые обосновывают его востребованность , , к которым можно отнести оптимальность по критерию минимума среднего квадрата ошибки оценки в классе любых оценок при условии наличия унимодальности и симметричности апостериорной плотности распределения , , используется рекуррентная оценка сигналов, что позволяет снизить требования к памяти устройств обработки информации. Однако фильтрация Калмана обладает и недостатками такими, как необходимость представления сигнала в пространстве состояний, требования к наличию марковского свойства оцениваемого процесса, отсутствие универсальности относительно коррелированных и некоррелированных помех измерения, необходимость решения уравнений Риккати, что заметно усложняет алгоритм, а также наличие обратной связи, приводящей к снижению запаса устойчивости фильтра.
В СПбГУАП на кафедре аэрокосмических измерительно-вычислительных комплексов был разработан новый финитно-временной метод фильтрации , , , , основанный на следствии теоремы ортогонального проецирования. Он не требует наличия свойств марковости оцениваемого процесса и представления сигнала в пространстве состояний, что делает его более универсальным , , . При определённой памяти процесса (при увеличении количества используемых предыдущих результатов измерения) дисперсия ошибки оценки совпадет с дисперсией фильтра Калмана. Финитно-временные алгоритмы имеют несколько модификаций: адаптивные и неадаптивные, с обратной связью и без неё , , , . Отсутствие обратной связи обеспечивает повышение устойчивости алгоритма. Финитно-временные методы фильтрации навигационных сигналов в условиях полной априорной неопределенности относительно полезного сигнала и помех легко реализуются как адаптивные алгоритмы . Задачей данного исследования является определение и сравнение динамических характеристик, показателей точности и робастности адаптивных финитно-временного без обратной связи и Калмановского методов фильтрации с неадаптивными методами в условиях широкой параметрической неопределённости.
2. Математическое описание исследуемых методов
Рассматривается линейная модель измерения, которая имеет вид: , , :
где i=1,2 … n, k=1, 2, Yi,k, Хi, Hi,k – случайные произвольные процессы.
Предполагается, что полезный сигнал не коррелирован с помехами и что помехи не коррелированы между собой, а также помехи имеют разные спектральные характеристики – одна высокочастотная (Hi1), другая низкочастотная (Hi2). Математическое ожидание всех процессов принято равным 0. Корреляционная функция помехи Hi2 неизвестна, а Hi1 представляет собой гауссовский белый шум, корреляционная функция которого имеет вид :
где δ – дельта-функция, ϭ – среднеквадратическое отклонения. В данной работе параметр ϭ считается неизвестным.
На вход фильтра разностного сигнала комплексной системы подаётся сигнал, описываемый следующим выражением :
В этом случае H2i является полезным сигналом, а Hi1 – помехой. Учитывая некоррелированность погрешностей, оценка неизвестной корреляционной функции осуществляется с помощью рекуррентного соотношения. Оптимальная матрица финитно-временного метода без обратной связи имеет вид :
Используя измерения (3), образуем вектор результатов наблюдения размерности n×r в i-й момент времени:
где zr = |z1r, z2r, zn-r| – векторы размерности n×1, r=i, i-1, … , i-k+1
Показатель точности финитно-временного алгоритма оценки сигнала Zi в i-ый момент времени вычисляется следующим образом :
где Tr – след матрицы, KℇЧopti – матрица корреляционных моментов ошибок оптимальных оценок размерности m∙k×m∙k.
Оптимальную по критерию минимума следа матрицы ошибок оценку X^*i в момент времени i можно вычислить по следующей формуле:
где матрица оптимальной оценки определяется следующим выражением :
являются векторами размерности, определяемыми текущими и предшествующими значениями сигналов H2,i и Zi.
Матрицу Kℇopti на основании следствия теоремы ортогонального проецирования представим как :
где – матрица r×r корреляционных моментов оптимальных оценок равна :
Матрица корреляционных моментов адаптивных оптимальных оценок представляется следующим образом:
3. Основные результаты
3.1. Исследование адаптивных финитно-временных и Калмановских методов фильтрации на точность и время переходного процесса
Моделирование проводится с помощью Mathcad 15. Исходные данные для моделирования:
1. Память процесса r = 4;
2. Объём выборки N = 2000;
3. Величина, обратная времени корреляции для барометрического измерителя высоты: α1 = 0,01 с-1 ;
4. Величина, обратная времени корреляции для радиотехнического измерителя высоты: α = 1 с-1 ;
5. Дискрет Котельникова: d = 4
На рисунке 1 представлены графики зависимости дисперсии ошибки оценки от времени.
DEA2 – дисперсия ошибки оценки адаптивного финитно-временного алгоритма без обратной связи
DEA12 – дисперсия ошибки оценки адаптивный алгоритм фильтрации Калмана
DE2 – дисперсия ошибки оценки финитно-временного алгоритма без обратной связи
DEK2 – дисперсия ошибки оценки алгоритма фильтрации Калмана
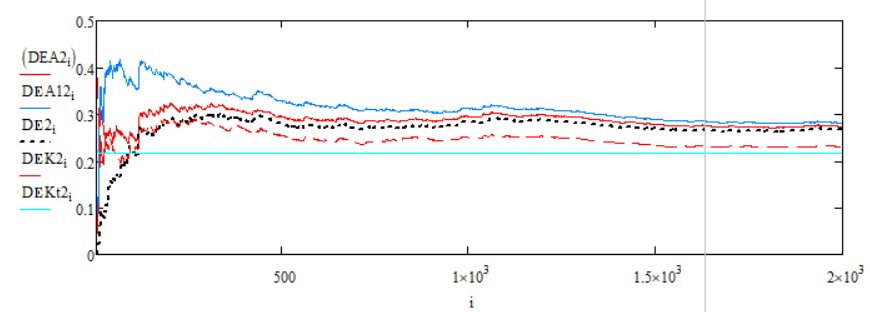
Рисунок 1 - Графики зависимости дисперсии ошибки оценки различных алгоритмов от времени
1. Адаптивный финитно-временной алгоритм без обратной связи: около 250 с;
2. Адаптивный фильтр Калмана: около 500 с;
3. Финитной-временной алгоритм без обратной связи: около 250 с;
4. Фильтр Калмана: около 500 с.
Оценим установившуюся величину дисперсии ошибки оценки каждого из алгоритмов с помощью вычислений в Mathcad:
1. Адаптивный финитно-временной алгоритм без обратной связи: 0,273;
2. Адаптивный фильтр Калмана: 0,281;
3. Финитной-временной алгоритм без обратной связи: 0,266;
4. Фильтр Калмана: 0,230.
Таким образом, адаптивный финитно-временной алгоритм без обратной связи незначительно уступает по точности неадаптивным финитно-временному и фильтру Калмана.
3.2. Исследование адаптивных финитно-временных и Калмановских методов фильтрации на робастность
Робастность – это малая чувствительность показателя качества к изменению параметров информационно-измерительной системы. В данном случае за показатель качества принята дисперсия ошибки оценки.
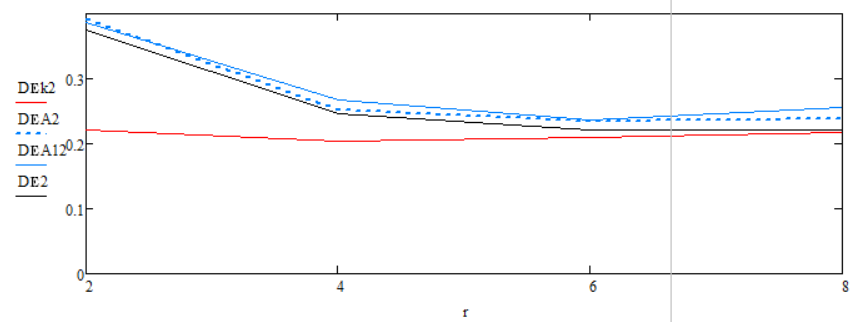
Рисунок 2 - Зависимость дисперсии ошибки оценки фильтров от изменения памяти процесса r при объёме выборки N = 2000
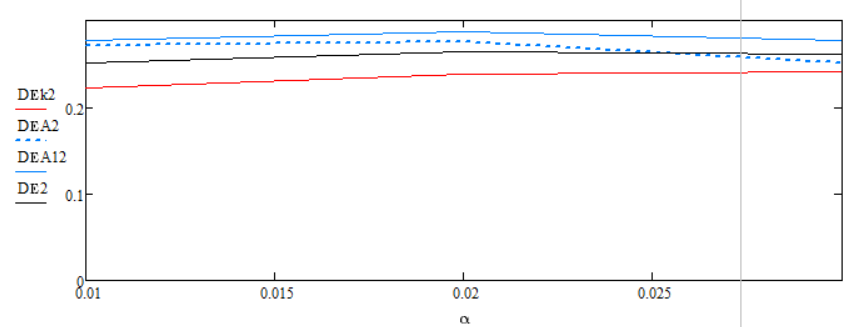
Рисунок 3 - Зависимость дисперсии ошибки оценки фильтров от изменения величины α
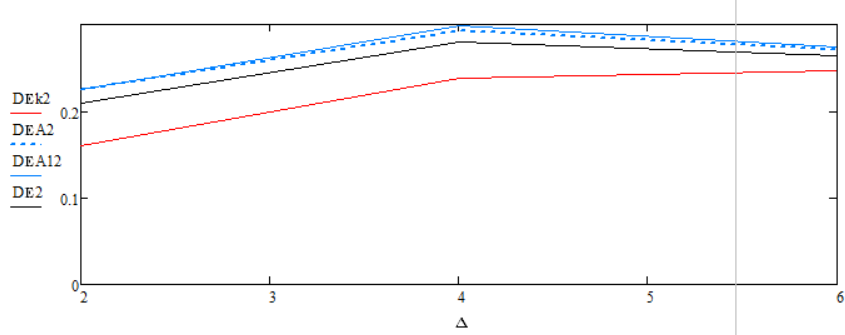
Рисунок 4 - Зависимость дисперсии ошибки оценки фильтров от изменения величины дискрета d
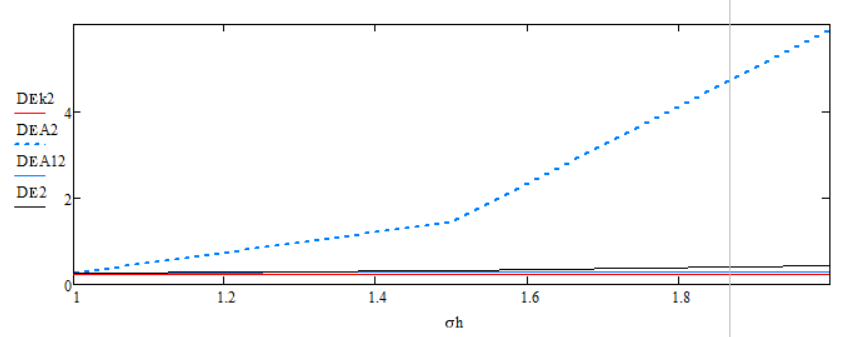
Рисунок 5 - Зависимость дисперсии ошибки оценки фильтров от изменения среднеквадратического отклонения помехи измерителей
Сравнительная характеристика исследуемых алгоритмов по показателю робастности представлена в таблице 2.
Таблица 1 - Сравнительная характеристика исследуемых адаптивных и неадаптивных алгоритмов по робастности
Параметр | Наиболее робастный (-ые) алгоритм (-ы) |
Память процесса r | Финитно-временной алгоритм |
α | Все исследуемые алгоритмы |
Дискрет d | Финитно-временной без обратной связи и адаптивный финитно-временной без обратной связи |
Среднеквадратическое отклонение помехи измерителей | Фильтр Калмана, адаптивный фильтр Калмана, финитно-временной без обратной связи |
4. Заключение
В данной работе были исследованы адаптивные и неадаптивные алгоритмы Калмана и финитно-временной обработки сигналов. Исследование показало, что в условиях широкой параметрической априорной неопределённости, когда неизвестна ни одна из двух погрешностей, адаптивные алгоритмы работают эффективно, незначительно уступая неадаптивным алгоритмам, обеспечивая вполне пригодные для комплексных систем характеристики по робастности, точности и времени переходного процесса.
