RAY MODEL OF ELASTIC WAVE TRAJECTORY IN INHOMOGENEOUS MEDIUM

В настоящее время одной из актуальных задач, связанных с распространением упругих волн в непрерывно неоднородных средах, является проблема неразрушающего ультразвукового контроля металлоизделий с упрочненным слоем, получаемым при их термической обработке

В известной научной литературе практически отсутствуют сведения о математической модели, описывающей траекторию упругих волн в непрерывно неоднородных средах. Поэтому целью настоящей работы является разработка этой модели и ее теоретическое исследование.

Рассмотрим твердую среду, структурно состоящую из упрочненного и неупрочненного слоев, разделенных переходной областью (рис. 1). Введем систему координат так, чтобы ось Oz была перпендикулярна границам рассматриваемых слоев. В этом случае направление оси Oz будет совпадать с направлением роста скорости упругих волн, т.е. с направлением градиента скорости.

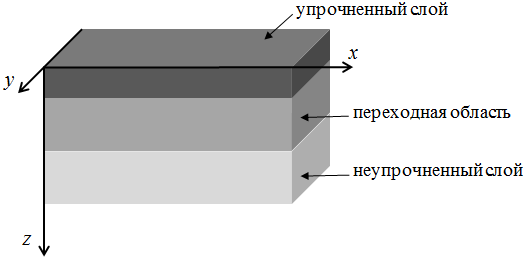
Рисунок 1 - Структурно-геометрическая схема рассматриваемой среды

DOI:10.60797/IRJ.2024.144.6.1

Пусть упрочненный слой и переходная область являются конечными в направлении оси z и бесконечными в двух других направлениях, а неупрочненный слой является полубесконечным. Рассмотрим распространение упругой волны в этой среде в виде акустического луча, распространяющегося в плоскости xOz и выходящего из начала координат под некоторым углом α0 к оси Ox. Так как в упрочненном и неупрочненном слоях градиент скорости упругих волн равен нулю (скорость не зависит от координат), то траекторией их распространения здесь будет прямая. В переходной же области наблюдается градиент скорости, и траектория луча здесь будет искривляться. Тогда в общем случае траектория акустического луча в рассматриваемой слоистой структуре будет иметь вид, как на рис. 2.

Для поиска уравнения, описывающего подобную траекторию, отвлечемся пока от слоистой структуры и рассмотрим по подробнее распространение упругих волн в переходной области. При этом будем пока полагать, что она является полубесконечной в направлении оси Oz и начало системы координат совпадает с ее границей, лежащей в плоскости xOy.

Для простоты рассуждений будем считать, что градиент скорости является постоянной величиной. Пусть при этом скорость будет зависеть только от координаты z. Тогда зависимость скорости от координаты можно записать в виде

(1)

где v0 – скорость упругой волны в точке с координатой z=0; A – феноменологический параметр, который характеризует градиент скорости.

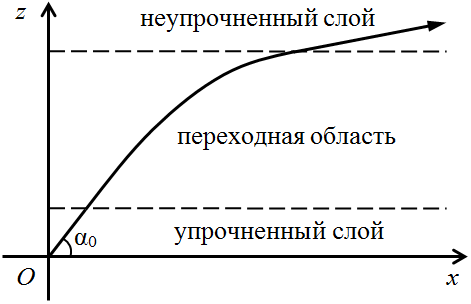
Рисунок 2 - Траектория акустического луча, прошедшего насквозь переходную область

DOI:10.60797/IRJ.2024.144.6.2

Очевидно, что в основе вывода уравнения траектории кроме формулы (1) должен быть закон Снеллиуса, который в нашем случае имеет вид

(2)

где α – угол между направлением скорости упругой волны и осью Ox в произвольной точке траектории, а v – модуль скорости упругой волны в этой же точке. Также при выводе уравнения траектории воспользуемся свойством производной от функции в некоторой произвольной точке, а именно

(3)

Таким образом, из системы уравнений (1)-(3) после некоторых математических преобразований получаем выражение

из которого после разделения переменных, интегрирования и математических преобразований получаем искомое уравнение траектории z(x) упругой волны в переходной области

(4)

Графиком полученного уравнения является кривая, схематично представленная на рис. 3. Из анализа графика следует, что он является симметричным относительно прямой параллельной оси Oz и проходящей через вершину этого графика. Поэтому если упругая волна входит в переходную область под углом α0 к оси Ox, то выходить из нее будет под углом (π-α0).

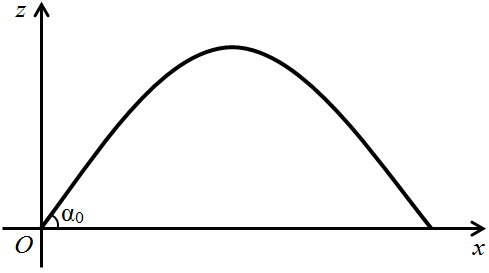
Рисунок 3 - Схематичный график уравнения (4): траектория упругой волны в переходной области

DOI:10.60797/IRJ.2024.144.6.3

Вернемся снова к слоистой структуре (см. рис. 1-2). Далее также будем полагать, что акустический луч входит в упрочненный слой под углом α0 к оси Ox в точке, совпадающей с началом координат. Так как сначала этот луч пройдет некоторый путь в упрочненном слое, то координаты точки его входа в переходную область будут смещены относительно нуля. Обозначим координаты этой точки как x=x1 и z=d. Тогда формулу зависимости скорости (1) упругой волны и уравнение траектории (4) в переходной области необходимо привести к виду

(5)

(6)

Следует заметить, что формулы (5) и (6) справедливы только для переходного слоя. В упрочненном и неупрочненном слое зависимости z(x) являются линейными, и их можно представить в виде

где  – координата по оси Oz границы между переходной областью и неупрочненным слоем; xD – координата по оси Ox точки пересечения акустическим лучом границы между переходной областью и неупрочненным слоем, которую можно определить, приняв в уравнении (6) z=D.

В результате из выше изложенного следует, что траектория акустического луча, изображенная на рис. 2, будет описываться кусочной функцией в виде

(7)

Однако при определенных условиях акустический луч может не пересечь границу z=D, а повернуть обратно в сторону упрочненного слоя и выйти из него (рис. 4). Для получения уравнения, описывающего эту траекторию, необходимо в формуле (7) изменить третью строку и скорректировать области определения координаты x во второй и третьей строках.

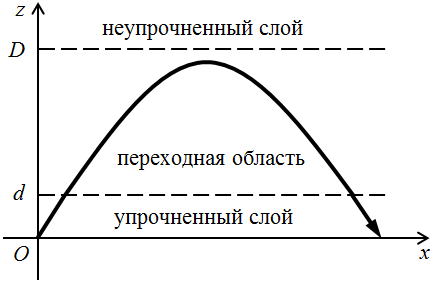
Рисунок 4 - Траектория акустического луча, развернувшегося в переходной области

DOI:10.60797/IRJ.2024.144.6.4

После преобразований получим

(8)

Здесь x2 – координата выхода акустического луча из переходной области обратно в упрочненный слой; b – координата по оси Ox выхода акустического луча из рассматриваемой трехслойной структуры.

Исследуем функцию (8) на экстремум и найдем координаты вершины графика этой функции:

(9)

(10)

С другой стороны, исходя из симметрии траектории, координату вершины можно найти как точку пересечения продолжения прямолинейных участков траектории из формулы (8):

Тогда, подставив последнее в формулу (9), получаем выражение для вычисления координаты выхода акустического луча из трехслойной структуры:

(11)

Уравнения (9) и (10), как и ожидалось, показывают, что координаты вершины траектории зависят от толщины упрочненного слоя, градиента скорости и угла α0, под которым акустический луч входит в рассматриваемую среду. Но так как толщина переходной области ограничена, то вершина траектории акустического луча может быть, либо действительной при zв≤D, либо мнимой при zв>D. Действительная вершина располагается в переходной области и лежит на траектории луча, а мнимая вершина располагается в неупрочненном слое и лежит на продолжении криволинейного участка траектории луча в неупрочненный слой.

Другими словами расчеты по формулам (9) и (10) дают не только информацию о координатах вершины траектории акустического луча, но и позволяют понять каким будет характер этой траектории – возвратный или сквозной. Очевидно, что при zв>D траектория будет сквозной, а при zв≤D – возвратной.

Для проведения модельных расчетов и построения траектории ультразвукового луча возьмем границы упрочненного и переходного слоев и значения скорости ультразвука характерные для стали: d=0,04 м, D=0,14 м, v0=5920 м/с, v=5980 м/с. Здесь v0 – скорость ультразвука в упрочненном слое и на его границе с переходной областью; v – скорость ультразвука в неупрочненном слое и на его границе с переходной областью. Тогда для градиента скорости ультразвука в переходной области можно записать выражение . Все расчеты будем проводить на основании уравнений, полученных в предыдущем разделе.

На рис. 5 представлены траектории ультразвука при различных значениях угла α0 в интервале от 1º до 10º с шагом 1º. Здесь точками обозначена граница упрочненного слоя, а пунктирной линией – граница переходного слоя. На рисунке видно, что траектория ультразвука сильно зависит от угла α0. Также следует заметить, что разным значениям угла α0 может соответствовать одна и та же точка обратного выхода траектории из рассматриваемой среды. На рисунке близкие к такому случаю являются две пары траекторий, соответствующие углам 2º и 7º, 3º и 4º. На этом рисунке также имеются траектории, которые насквозь проходят переходный слой и не возвращаются обратно (траектории соответствующие углам 9º и 10º).

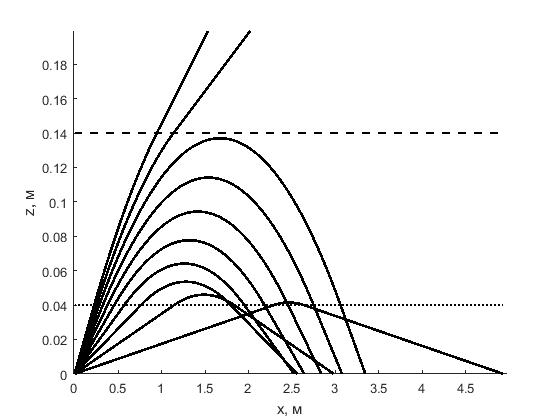
Рисунок 5 - Траектории ультразвука при значениях угла α0 = 1º–10º с шагом 1º

DOI:10.60797/IRJ.2024.144.6.5

Анализ траекторий, у которых совпадают точки обратного выхода из упрочненного слоя (рис. 6), показывает, что их углы входа удовлетворяют следующему уравнению:

Кроме этого анализ также показывает, что углы α0 и β будут равны друг другу, если толщина упрочненного слоя будет соответствовать двум третьим толщины всей двухслойной структуры, т.е. 

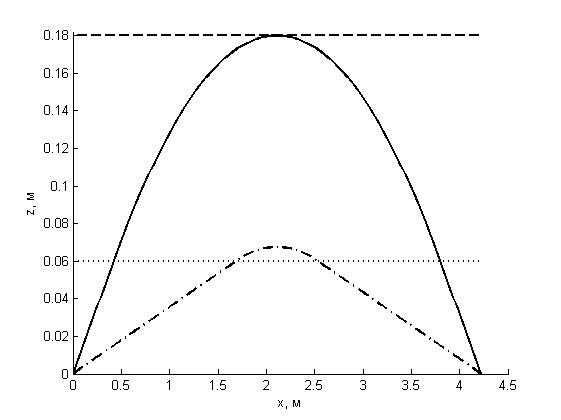
Рисунок 6 - Траектории ультразвука с одной точкой выхода

Примечание: горизонтальным линиям соответствуют границы упрочненного и переходного слоев

DOI:10.60797/IRJ.2024.144.6.6

В этом случае характер зависимости траекторий от угла ввода будет немного отличаться от представленного на рис. 5. Иллюстрация этого случая представлена на рис. 7. Здесь с увеличением угла наблюдается только уменьшение расстояния между точками входа и выхода траектории, и отсутствуют траектории, у которых совпадали бы точки выхода из упрочненного слоя

Далее проведем расчет зависимости траектории ультразвукового луча от толщины упрочненного слоя и толщины переходной области. Для этих вычислений в качестве исходных данных будем использовать те же значения скоростей. Значение угла α0 возьмем 8º, что соответствует траектории из рис. 5, у которой вершина почти касается границы z=D.

На рис. 8 представлены результаты расчета траектории ультразвука в зависимости от различных значений толщины переходного слоя D. Здесь также точками указана граница упрочненного слоя, а пунктирными линиями указаны задаваемые положения границы переходного слоя. Из рисунка видно, что значение D очень сильно влияет на траекторию ультразвука и, как следствие, сильно влияет на положение точки обратного выхода ультразвука из рассматриваемой среды. При этом чем меньше толщина переходного слоя, тем меньше расстояние между точками входа и выхода траектории ультразвука в рассматриваемой среде. Из результатов расчета следует, что изменение толщины переходного слоя на 3 см приводит к смещению точки выхода траектории на величину порядка 80–90 cм.

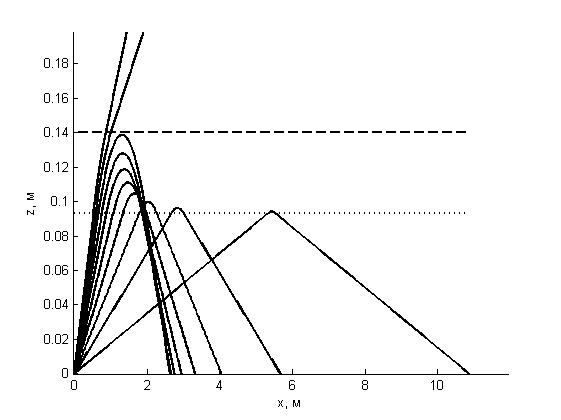
Рисунок 7 - Траектории ультразвука при d = 2D/3 и значениях угла α0=1º–10º с шагом 1º

DOI:10.60797/IRJ.2024.144.6.7

На рис. 9 представлены результаты расчета траектории ультразвука в зависимости от различных значений толщины упрочненного слоя d. Как и на предыдущих рисунках, здесь пунктирной линией обозначена граница переходного слоя, а точками указаны задаваемые положения границы упрочненного слоя. Из рисунка видно, что при неизменном положении границы переходного слоя (z=D) увеличение толщины упрочненного слоя приводит к уменьшению толщины переходной области. Здесь фактически представлены результаты расчета траекторий в зависимости от одновременного изменения размеров обоих слоев рассматриваемой структуры при неизменной их общей толщине, т.е. при D=const. Результаты показывают, что увеличение толщины упрочненного слоя приводит к незначительному увеличению координаты вершины траектории zв – вершина траектории становится ближе к границе переходного слоя z=D. При этом расстояние между точками входа и выхода ультразвука в рассматриваемой среде уменьшается, что говорит о более сильном влиянии на траекторию изменения толщины переходной области по сравнению с изменением толщины упрочненного слоя.

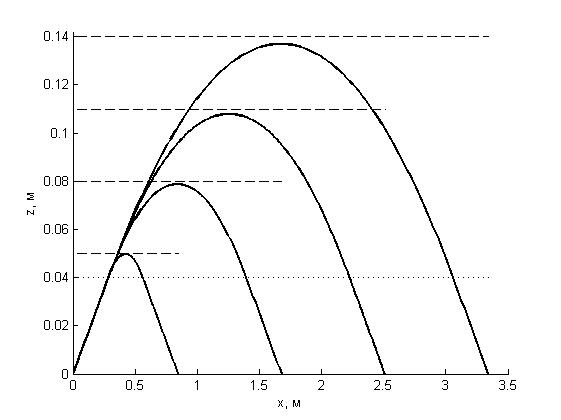
Рисунок 8 - Траектории ультразвука при значениях толщины переходного слоя: D = 0,05–0,14 м, шаг равен 0,03 м

DOI:10.60797/IRJ.2024.144.6.8

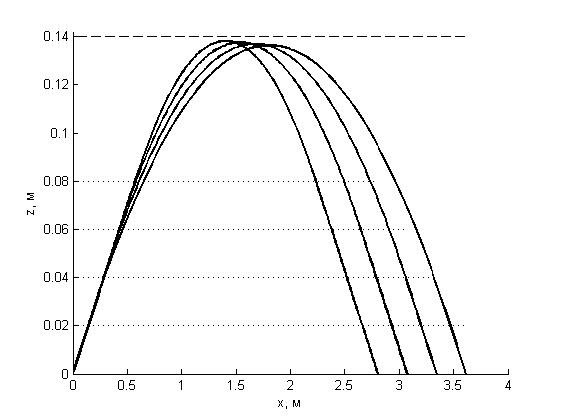
Рисунок 9 - Траектории ультразвука при значениях толщины упрочненного слоя: d = 0,02–0,08 м, шаг равен 0,02 м

DOI:10.60797/IRJ.2024.144.6.9

Из всех возможных траекторий ультразвука в рассматриваемой структуре наибольший интерес представляет такая, у которой вершина касается границы переходной области с неупрочненным слоем, т.е. координата вершины которой удовлетворяет условию zв=D. При проведении анализа этой траектории выяснилось, что независимо от толщины упрочненного слоя и переходной области вершина траектории всегда будет касаться границы z=D, если ввести луч в рассматриваемую структуру под углом, удовлетворяющим уравнению: 

где . Т.е. этот угол зависит только от скоростей ультразвука на границах переходного слоя z=d и z=D.