MODELING OF PHOSPHORENE WITH CLASSICAL MOLECULAR DYNAMICS USING DEEP LEARNING
MODELING OF PHOSPHORENE WITH CLASSICAL MOLECULAR DYNAMICS USING DEEP LEARNING
Abstract
In this article, an attempt was made to construct a model of black phosphorene interatomic interaction potentials using deep learning. A feedforward neural network architecture provided by the DeePMD package was selected for this purpose. The training data were collected from the results of ab initio molecular dynamics simulations. The constructed force field model was subsequently utilized in the classical molecular dynamics simulations. The density of phosphorene in the resulting computer model is approximately equal to 2.72 g/cm3, and its thermal conductivity coefficients were found to be 1.685 W/(m·K) and 2.552 W/(m·K) along the "armchair" and "zigzag" directions, respectively. The determined physical properties of black phosphorene are adequately consistent with the corresponding real values.
1. Введение
Фосфорен является двумерным материалом, который может быть синтезирован из чёрного фосфора
. Интерес к нему обусловлен, в частности, тем, что он имеет ненулевую ширину запрещённой зоны, а многие физические свойства фосфорена зависят от количества слоёв и проявляют анизотропию.Множество работ
, , по исследованию фосфорена было проведено с помощью методов компьютерного моделирования, в основном используются первопринципные (ab initio) подходы. Но не так часто встречаются работы по моделированию фосфорена методом классической молекулярной динамики (МД), поскольку для проведения такой компьютерной симуляции необходима модель потенциалов – численная аппроксимация потенциалов и силовых полей межатомного взаимодействия.Известно, что глубокое обучение широко распространено в современных технологиях
, , а его использование в физике конденсированного состояния является многообещающим. Так, например, с помощью нейронных сетей возможно построить модель потенциалов, что и будет проделано в данной работе.Дополнительно, мы определим коэффициент теплопроводности фосфорена в компьютерной модели и сравним его с экспериментальными данными .
2. Метод построения компьютерной модели фосфорена
Первым шагом для построения компьютерной модели фосфорена является получение данных для обучения нейронной сети, такими данными выступают результаты первопринципного моделирования.
В 1985 году Кар и Парринелло предложили метод МД
, основой которого является совместное рассмотрение системы электронов и ионов. Движение ядер атомов задаётся классически, оно описывается эволюцией координат {RI} ядер, а электронные степени свободы – квантово-механическими волновыми функциямиПусть после проведения моделирования методом молекулярной динамики Кара-Парринелло (МДКП) системы, состоящей из N атомов, мы имеем информацию о системе в разные моменты времени: координаты атомов , полную энергию системы E, силы, действующие на i-й атом Fi и т.д.
Метод DeePMD позволяет установить зависимость полной энергии от позиций атомов друг относительно друга:
Здесь – матрица относительных координат – расстояний от атома i до атома j внутри некоторого радиуса взаимодействия rc:
Зависимость энергий Es(i) от матрицы относительных координат выстраивается в два шага: сначала по матрице строится матрица признаков, в оригинале называемая дескриптором
, с целью сохранения поступательной, вращательной и перестановочной симметрии системы; затем подгоняется такая нейронная сеть, что
, она называется подгоночной (FNN).
В данном методе дескриптор строится также через нейронную сеть , называемую вложением (ENN).
Обе сети (ENN и FNN
) являются обычными нейронными сетями с прямой связью, содержащие несколько скрытых слоёв.
В методе классической МД задача движения атомов решается путем вычисления траектории движения r(t) с помощью уравнений Ньютона:
где Fi(r) – суммарная сила, действующая на i-ю частицу:
U(r) – потенциальная энергия межатомного взаимодействия
.Так как энергия U(r) задана численно нейронными сетями, уравнения (3) просто решаются численными методами.
3. Метод определения коэффициента теплопроводности
![Схема распределения тепла в листе фосфорена размером [2L×10] нм2](/media/images/2024-03-20/dc8904e1-6a01-4128-9fb7-554794a6c540.jpg)
Рисунок 1 - Схема распределения тепла в листе фосфорена размером [2L×10] нм2
Согласно закону теплопроводности Фурье:
где ϰ – коэффициент теплопроводности, T – температура, q – вектор плотности теплового потока, скаляр которого описывается уравнением
здесь dQτ – пройденное количество тепла через единицу площади dS поперечного сечения за единицу времени dτ.
Примем, что пройденное через поперечное сечение количество теплоты Qτ за всё время (или за какой-то промежуток времени) Δt моделирования равно теплоте, переданной нагревающейся области за это же время:
Величина W делится на 2, поскольку тепло распространяется в двух направлениях.
Модуль градиента температуры можно представить как среднюю разность температур тёплого и холодного регионов, отнесённую к расстоянию L:
где N – количество взятых разностей в различные промежутки времени.
После некоторого времени t с начала моделирования устанавливается постоянный температурный градиент, тогда-то и будем вычислять коэффициент теплопроводности, который, учитывая соотношения (5), (6), (7) и (8), выразим в следующем виде:
В предположении с изменением длины образца 2L пропорционально изменяется время t, за которое установится неизменный со временем температурный градиент. То есть, пропорционально изменится и разность температур 〈ΔT〉. Таким образом, предполагается, что отношение 〈ΔT〉/L не изменяется для различных расстояний L.
4. Проведение моделирования
Сперва, как было ранее обозначено, проведём моделирование методом МДКП при помощи пакета программ Quantum-ESPRESSO, который использует специальные скрипты в качестве входных файлов
. Элементарная ячейка, участвующая в этом моделировании показана на рисунке 2.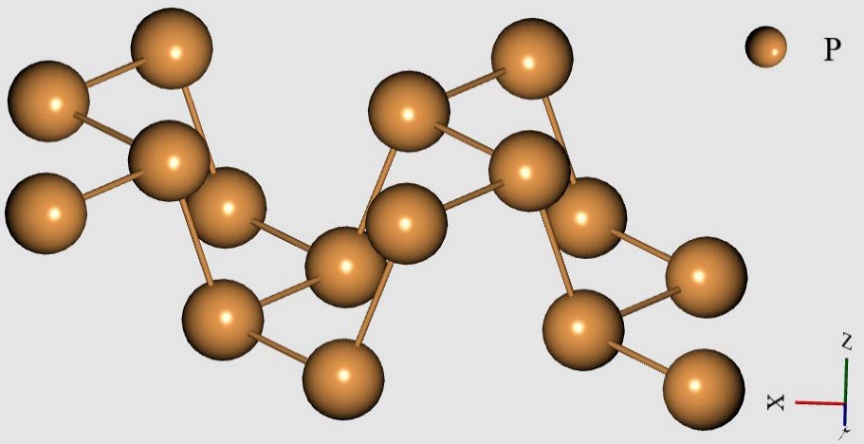
Рисунок 2 - Элемент кристаллической решётки фосфорена, участвующий в моделировании методом молекулярной динамики Кара-Парринелло
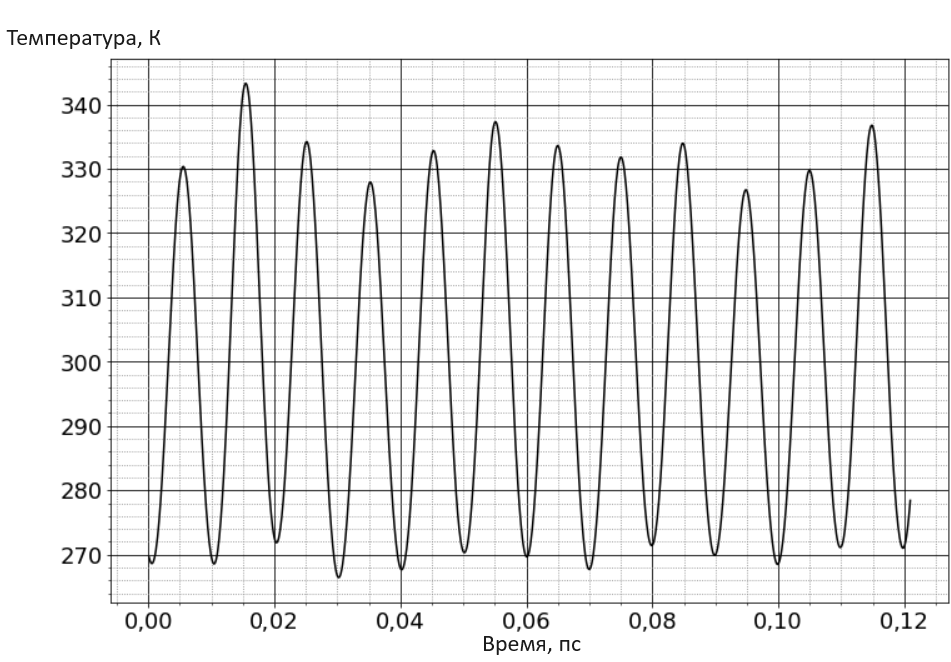
Рисунок 3 - Изменение температуры со временем в обучающей выборке
Скрытые слои нейросетей и количество нейронов в них задавалось следующим: ENN: [10,20,40]; FNN: [200,100,60,30,10].
Максимальный радиус взаимодействия принят равным rc=6 Å.
Количество шагов обучения: 100000.
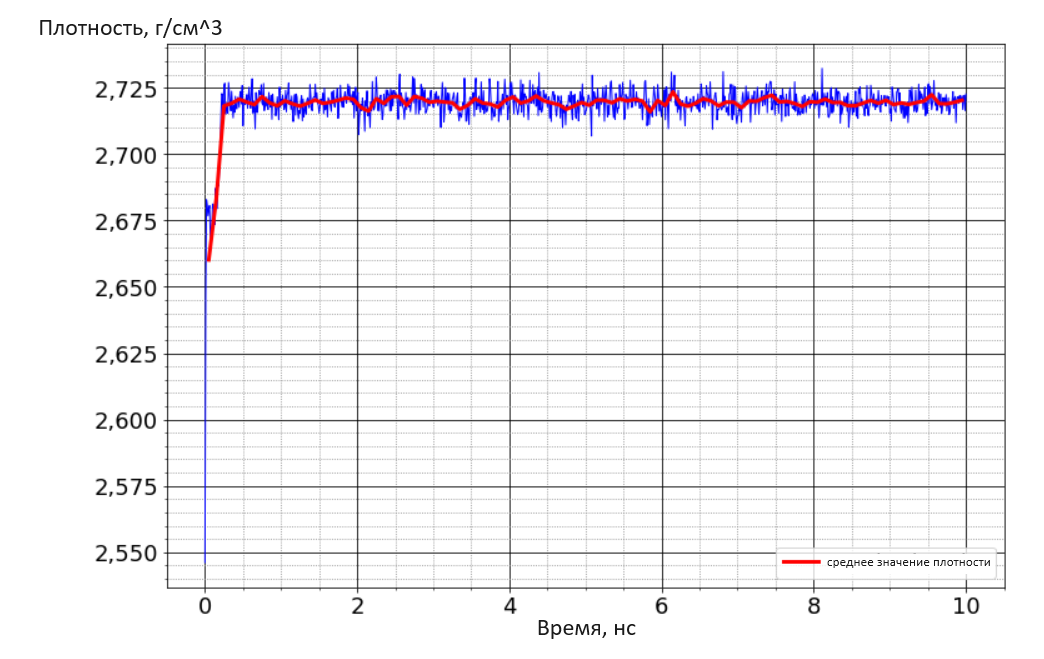
Рисунок 4 - Изменение плотности фосфорена со временем в моделировании методом классической молекулярной динамики
Для вычисления коэффициента теплопроводности фосфорена мы провели моделирование по описанной схеме (рисунок 1, уравнения 6-10) несколько раз, изменяя при этом длину образца 2L={20,30,40,50,60,70,80} нм. Результаты вычислений показаны на рисунке 5.
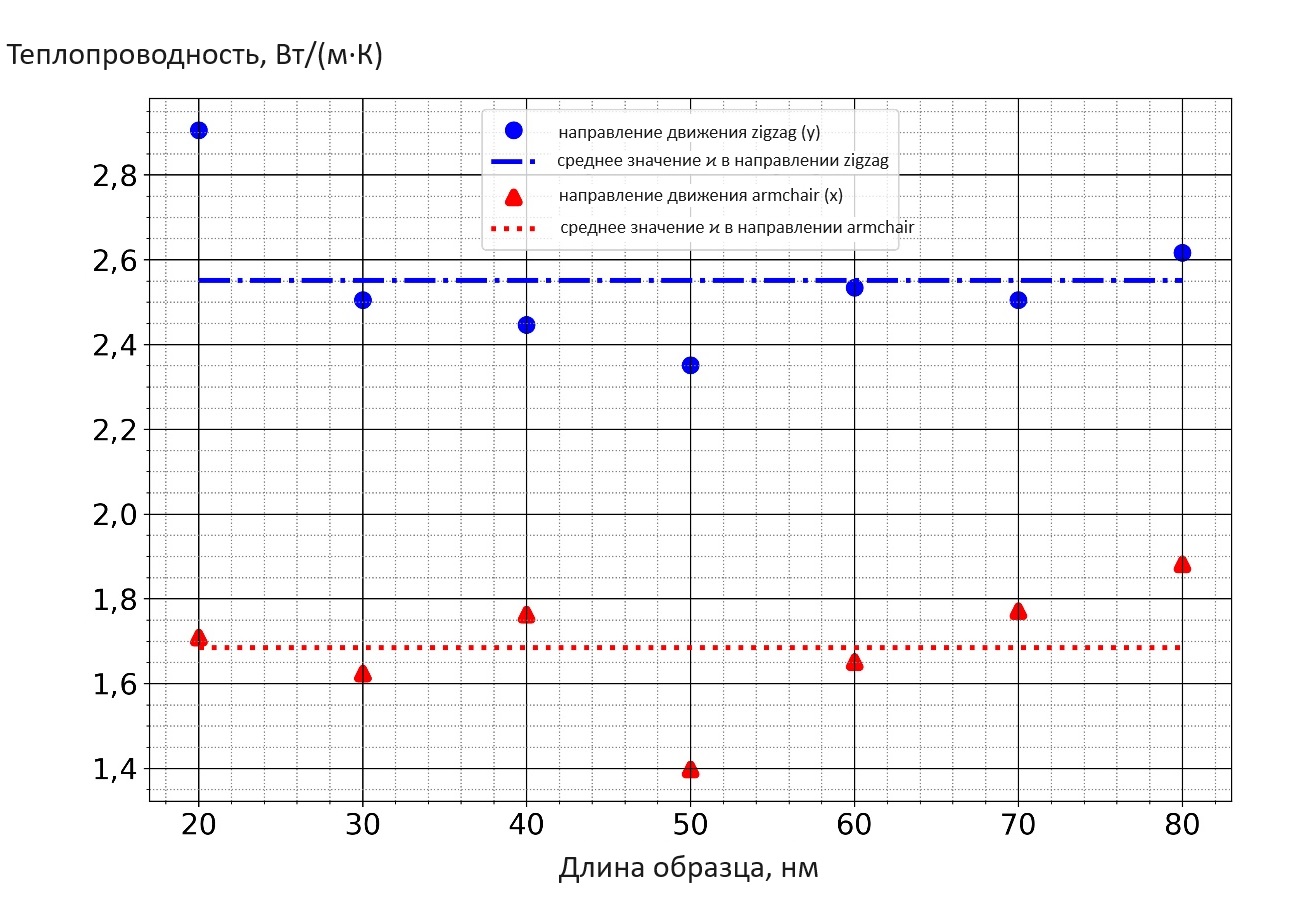
Рисунок 5 - Значения коэффициента теплопроводности фосфорена при его различной продольной длине 2L в разных направлениях
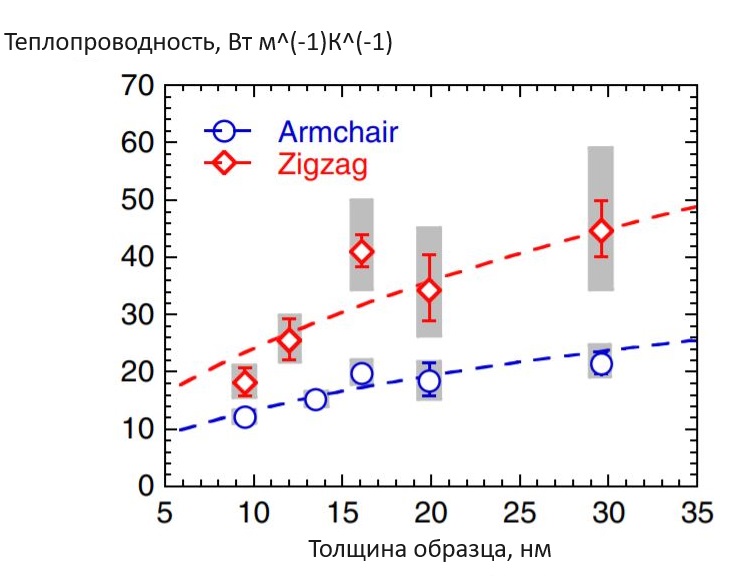
Рисунок 6 - Зависимость коэффициента теплопроводности от толщины образца чёрного фосфора
Примечание: по ист. [7]
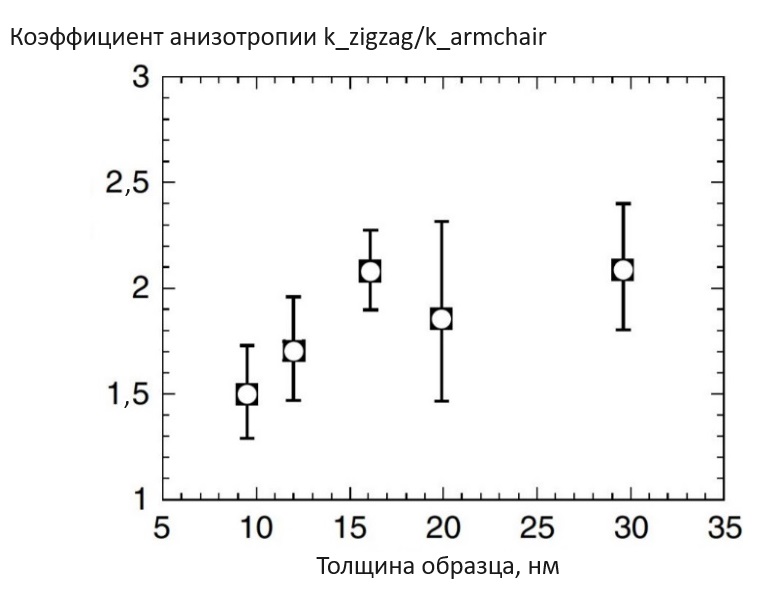
Рисунок 7 - Зависимость отношения ϰy/ϰx от толщины образца чёрного фосфора
Примечание: по ист. [7]
5. Заключение
Результаты вычислений, проведённых в работе, показывают высокую стабильность фосфорена в полученной компьютерной модели, а извлечённые физические свойства с достаточной точностью повторяют свойства реального материала.
