An analysis of sentence and word lengths in the annual speeches of UK party leaders
An analysis of sentence and word lengths in the annual speeches of UK party leaders
Abstract
Sentence lengths and word lengths in the annual speeches of UK party leaders were analysed. Transcripts of 224 speeches delivered between 1895 and 2018 were used for the analysis. It was found that the average sentence length in the speech decreases linearly with a slope of 0.14 ± 0.01 words per year, and the distribution of sentence lengths best obeys the Weibull distribution among those analysed (Weibull, Log Normal, Rayleigh, Folded Normal, Half Normal, Normal). It is suggested that the results obtained are explained by the principle of least effort. The average word length practically does not change with time (the mean value either does not change or changes insignificantly), and the distribution of word length in contrast to sentence length is better described by a lognormal distribution compared to, for example, Weibull or Poisson distributions.
1. Введение
Важной отраслью науки является количественная лингвистика, которая использует математические методы для установления законов, по которым функционирует язык. Такие законы, найденные в основном статистическими методами, указывают на существующие закономерности между различными элементами языка (фонемами, словами и т. д.). Предметом данного исследования является анализ распределений во времени длины предложений, измеряемой количеством слов, и длины слов, измеряемой количеством букв. Эти величины изучаются уже давно и используются для определения авторства произведения, жанра текста, когнитивного развития автора или читателя (слушателя), уровня владения языком и т. д.
, , , . Ранее, анализируя тексты публичных выступлений президентов США, мы обнаружили, что длина предложений в среднем уменьшается со временем, а само распределение длин предложений подчиняется распределению Вейбулла . Интересно подтвердить эти выводы на более крупной выборке. Второй целью данной работы является проверка полученных результатов для длин предложений на длинах слов.Для анализа используются электронные архивы публичных выступлений, а именно ежегодные речи лидеров партий Великобритании с 1895 по 2018 год.
2. Исходные данные и анализ
Было проанализировано 224 ежегодных выступления лидеров партий Великобритании с 1895 по 2018 год, доступных в электронном архиве
.Речи лидеров партий Великобритании неравномерно распределены по времени из-за авторских прав, появления новой крупной партии в парламенте в 1977 году и некоторым другим причинам. В результате, речи Великобритании распределены: одна речь за 1895, 1896, 1899-1902, 1904-1906, 1911, 1918, 1919, 1923, 1926, 1930, 1933-1937, 1941-1943, 1945-1951, 1955-1958, 1960-1962, 1964, 1974 годы; две речи за 1897, 1903, 1907-1910, 1912,1913, 1920-1922, 1925, 1927-1929, 1932, 1963, 1965-1973, 1975, 1976, 1989-1991, 1995, 1997 годы; три речи за 1924, 1978-1981, 1983-1986, 1988, 1922-1994, 1996, 1998, 2000-2005, 2007-2018 годы и четыре речи за 1977, 1982, 1987, 1999, 2006 годы. Речи Великобритании за 1898, 1914-1917, 1931, 1938-1940, 1944, 1952-1954, 1959 годы не обработаны.
Первоначальная подготовка текстов включала проверку на наличие инициалов и объединение их в одно слово; замену всех многоточий, восклицательных и вопросительных знаков, обозначающих конец предложения, точками; удаление точек и запятых, используемых для написания чисел. Единицей измерения является слово, заключенное между пробелами, длина предложений измеряется количеством слов. В дальнейшем тексты обрабатывались автоматически с помощью специальной компьютерной программы. Статистический анализ проводился в программе Statistica 12.0 (TIBCO Software), MATLAB (The MathWork).
Средняя длина предложения рассчитывалась следующим методом: общее количество слов во всех предложениях делится на общее количество предложений. Согласно рис. 1, средняя длина предложений линейно уменьшается с течением времени (наклон линии составляет 0.14±0.01). Так, с 1918 года средняя длина предложения составляет около 27.9, а с 2018 года – около 13.8 слов, то есть длина уменьшилась в 2 раза.
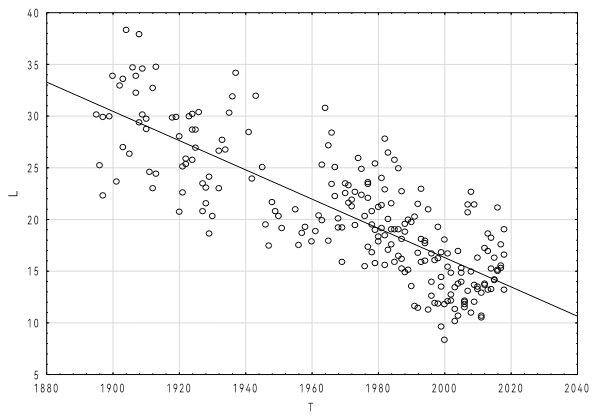
Рисунок 1 - Средняя длина предложения (L) в зависимости от времени речи (T)
Примечание: уравнение линейной регрессии имеет вид L = 299-0.14*T
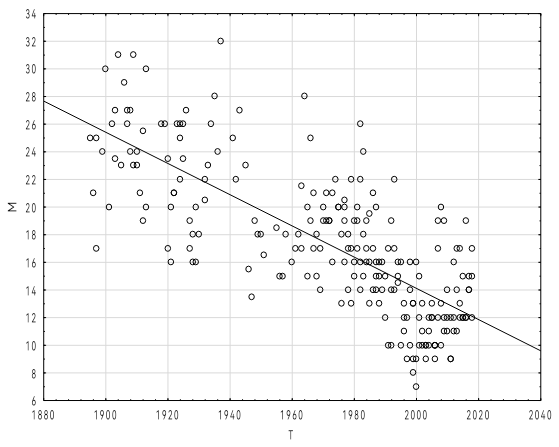
Рисунок 2 - Медиана (M) в зависимости от времени речи (T)
Примечание: уравнение линейной регрессии имеет вид M = 240-0.11*T
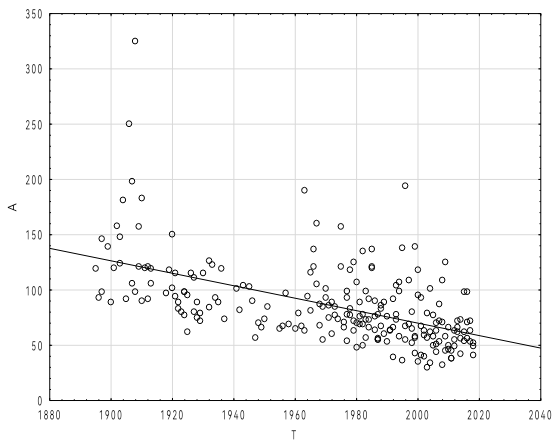
Рисунок 3 - Максимальная длина предложения (A) в зависимости от времени речи (T)
Примечание: уравнение линейной регрессии A = 1197-0,56*T
Для выбора наилучшего теоретического распределения, описывающего исследуемые эмпирические распределения, были отобраны 5 распределений, имеющих не более 2 параметров: LogNormal, Weibull, FoldedNormal, HalfNormal (Normal), Rayleigh. Ранжирование этих распределений по качеству описания данных проводилось на основе теста Колмогорова-Смирнова: чем больше значение p-уровня, тем лучше это распределение описывает эмпирические данные и, соответственно, тем выше его место по сравнению с другими. В таблице 1 показано, сколько раз одно из пяти оцененных распределений оказывалось в числе лучших, занимая 1, 2 или 3 место.
Таблица 1 - Ранжирование распределений по тесту Колмогорова-Смирнова
Место | Weibull | Log Normal | Rayleigh | Folded Normal | Normal | Half Normal |
number of speeches | ||||||
1 | 144 | 62 | 4 | 2 | 0 | 1 |
2 | 47 | 43 | 27 | 23 | 1 | 7 |
3 | 2 | 20 | 14 | 16 | 11 | 8 |
∑ | 193 | 125 | 45 | 41 | 12 | 16 |
Например, распределение Вейбулла для 144 выступлений оказалось на 1-м месте, для 47 выступлений – на втором и для 2 выступлений – на третьем. Таким образом, это распределение появилось во всех речах на первых трех местах. Более того, распределение Вейбулла достаточно хорошо описывает все выступления. Так, средний уровень значимости модели вероятностного распределения для речей, где Вейбулл на первом месте, 0.43 (144 речи), на втором месте 0.25 (47 речей), а на третьем 0.3 (2 речи). Если рассматривать логнормальное распределение, которое описывало 125 выступлений на первых трех местах, то средние уровни значимости составили 0.39 (для первых мест), 0.18 (для вторых мест) и 0.18 (для третьих мест).
Таким образом, на основе проведенного статистического анализа распределение Вейбулла оказывается наиболее предпочтительным для описания исследуемых выступлений. Функция распределения Вейбулла равна 1-exp(-(x/λ)k), где λ и k – параметры масштаба и формы, соответственно. По результатам анализа текста значение параметра k оказалось равным 1.7±0.2. Как следует из рисунка 4, параметр масштаба значительно уменьшается с течением времени. Поскольку известно, что этот параметр прямо пропорционален среднему, медиане и моде для распределения Вейбулла, это еще раз подтверждает высказанное выше утверждение о снижении средней (а также наиболее вероятной) длины предложения.
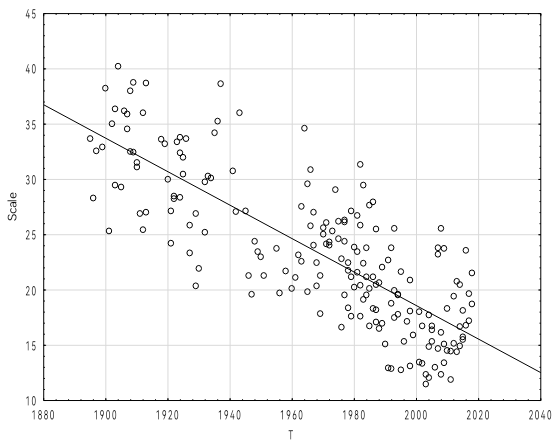
Рисунок 4 - Параметр масштаба распределения Вейбулла в зависимости от времени речи T
Примечание: уравнение линейной регрессии Масштаб = 321.5-0.15*T
Средняя длина слова рассчитывалась следующим методом: общее количество букв во всех словах делится на общее количество слов. График средней длины представлен на рис. 5. Из-за неравномерной плотности распределения выборки, какое-то видимое изменение в средней длине слова заметно с 1960 по 2020. Так с 1960 по 1980 средняя длина слова составляла 4.6, а с 2000 по 2020 – 4.5, однако с 1920 по 1960 средняя длина слова равна 4.5. Таким образом подобного линейного уменьшения как у средней длины предложения не наблюдается. Общая средняя длина слова составляет 4.5.
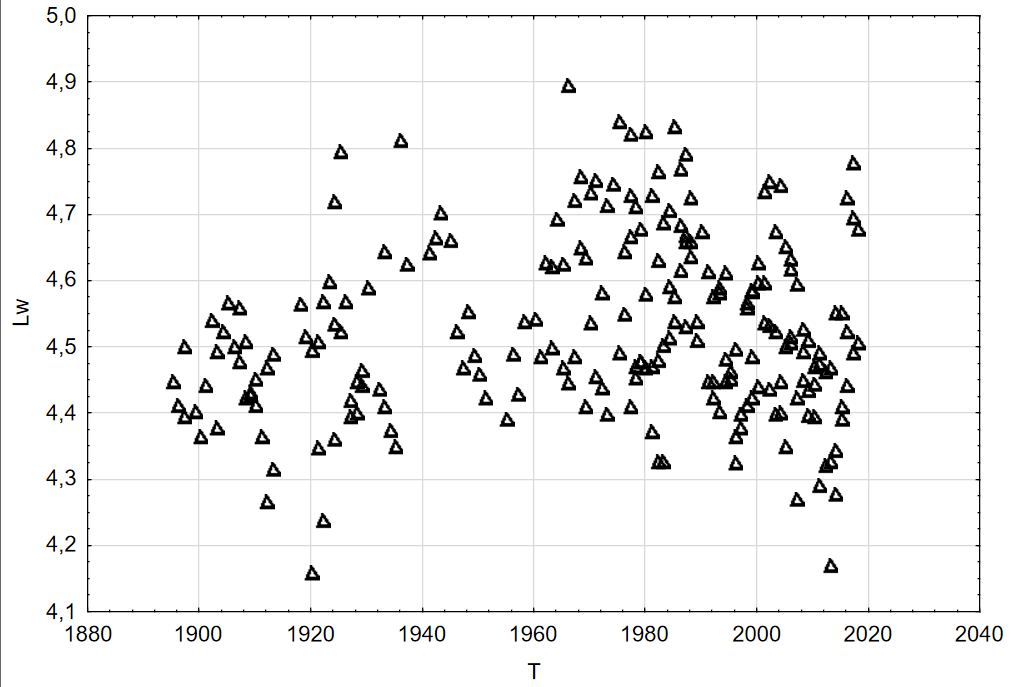
Рисунок 5 - Средняя длина слова (Lw) в зависимости от времени речи (T)
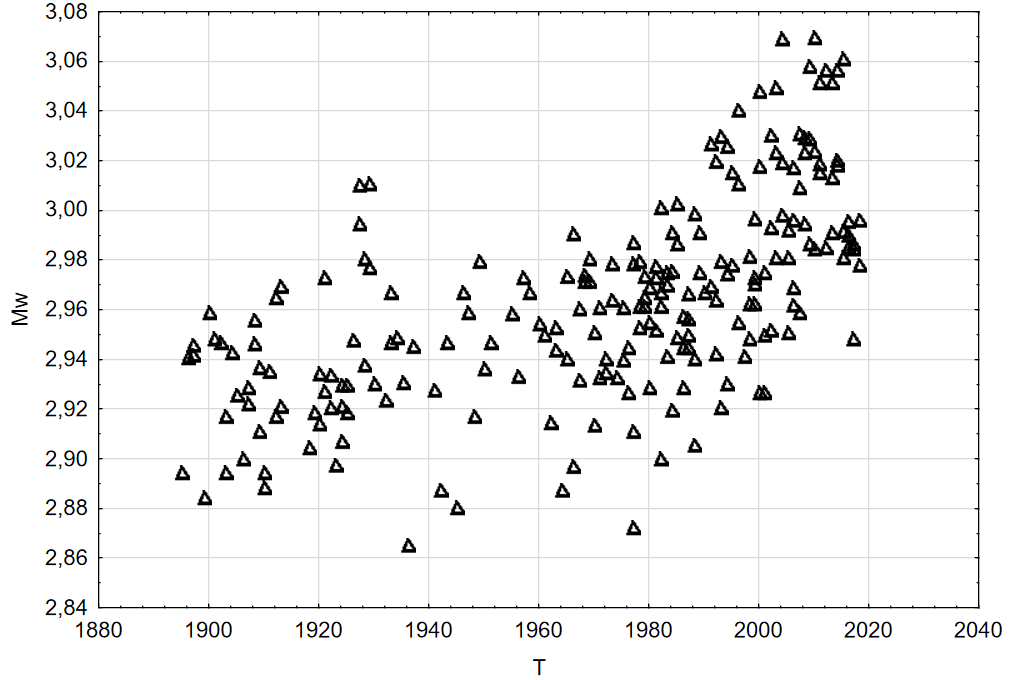
Рисунок 6 - Мода (Mw) в зависимости от времени речи (T)
Примечание: уравнение линейной регрессии Mw = 0.0006+ 1.6*T
Для выбора теоретического распределения были рассмотрены те же распределения, что и для длин предложений: LogNormal, Weibull, FoldedNormal, HalfNormal (Normal), Rayleigh. Ранжирование этих распределений по качеству описания данных проводилось на основе коэффициента детерминации, чем ближе значение R2 к 1, тем лучше это распределение описывает эмпирические данные и, соответственно, тем выше его место по сравнению с другими.
Таблица 2 - Ранжирование распределений по коэффициенту детерминации
Место | Log Normal | Weibull | Rayleigh | Folded Normal | Half Normal (Normal) |
number of speeches | |||||
1 | 210 | 11 | 0 | 0 | 0 |
2 | 11 | 210 | 0 | 0 | 0 |
3 | 0 | 0 | 94 | 127 | 0 |
∑ | 221 | 221 | 94 | 127 | 0 |
Как видно из таблицы, распределение Вейбулла здесь занимает 2 место. Лучше длину слов описывает логнормальное распределение, занимая первое место в 210 выступлениях из 221. В оставшихся 11 лучше описывает Вейбулл. Однако, следует отметить, что коэффициенты детерминации для этих распределений существенно не различаются. Среднее значение коэффициента для логнормального распределения составило 0.998, а для распределения Вейбулла – 0.996.
3. Заключение
На основе подсчета длины предложений ежегодных речей лидеров партий Великобритании за 123 года получены результаты:
1. Средняя длина предложения речи уменьшается линейно с наклоном 0.14 ± 0.014 слова в год, и в среднем с 1918 по 2018 год длина предложения уменьшилась с 27.9 до 13.8 слова.
2. Распределение длины предложений лучше описывается распределением Вейбулла (в частности, по сравнению с логнормальным).
Эти два результата согласуются с принципом наименьших усилий
: говорящий, стремясь минимизировать как свои усилия, так и усилия слушателя, старается выбрать наименьшую длину предложения из возможного набора предложений примерно одинакового содержания. В результате, с одной стороны, распределение предложений по длине начинает соответствовать распределению минимальных значений – распределению Вейбулла, а с другой стороны, в интервалах значительно большего времени подготовки речи средняя длина предложений сама уменьшается.3. Средняя длина слова в публичных выступлениях лидеров партий Великобритании практически не менялась и составила 4.5.
4. Распределение длины слова лучше описывается логнормальным распределением.
Как следствие, мы можем сделать вывод, что принцип наименьших усилий не оказывает существенного влияния на длину слов, используемых политиками. Важной причиной появления логнормального распределения является наличие мультипликативного случайного процесса, который определяет случайную величину
. В нашем случае такой случайной величиной является длина слова. Этот результат существенно отличается от результатов, полученных ранее для длин предложений, длина которых значительно уменьшалась с течением времени .