CHAOS AND INSTABILITY IN NONLINEAR ELECTRON GENERATOR
Перевозников Е.Н.1, Скворцов Г.Е.2
1Кандидат физико-математических наук, доцент,
Военно-космическая академия им. А.Ф. Можайского;
2 Кандидат физико-математических наук, старший научный сотрудник,
Санкт-Петербургский государственный университет
НЕУСТОЙЧИВОСТЬ И ХАОС В НЕЛИНЕЙНОМ ЭЛЕКТРОННОМ ГЕНЕРАТОРЕ
Дается пример приложения теории неустойчивости к описанию динамических режимов электронного генератора с туннельным диодом, имеющим N- образную вольтамперную характеристику. Такие генераторы являются существенно неравновесными системами и обладают явно выраженной хаотической динамикой. Для анализа динамических режимов в генераторе используется сингулярно-динамический метод и критерии неустойчивости и хаоса сформулированных авторами ранее. Получены общие условия возникновения в генераторе неустойчивых хаотических колебаний. Показано, что в окрестности экстремумов вольтамперной характеристики возникают неустойчивые хаотические колебания соответствующие наблюдаемым режимам в эксперименте.
Ключевые слова: нелинейные электронные генераторы, методы теории неустойчивости, неустойчивые хаотические режимы.
Perevoznikov E.N.1, Skvortsov G.E.2
1PhD in Physics and Mathematics, Associate professor,
Mozhaisky Military Space Academy;
2PhD in Physics and Mathematics, Senior Researcher,
St. Petersburg State University
CHAOS AND INSTABILITY IN NONLINEAR ELECTRON GENERATOR
Abstract
The example of applying the instability theory to the description of dynamic modes of an electronic generator with a tunnel diode having an N-shaped volt-ampere characteristic is given in the paper. Such generators are essentially non-equilibrium systems and have pronounced chaotic dynamics. The singular dynamic method and the criteria for instability and chaos formulated by the authors earlier are used for the analysis of dynamic regimes in the generator. General conditions for the appearance of unstable, chaotic oscillations in the generator are obtained. It is shown that unstable, chaotic oscillations corresponding to the observed regimes in the experiment appear in the vicinity of extremes of the current-voltage characteristic.
Keywords: nonlinear electronic generators, methods of the theory of instability, unstable, chaotic regimes.
Введение, постановка задачиПредставленная работа посвящена актуальным проблемам анализа режимов функционирования КПР (Кияшко, Пиковского, Рабиновича) генераторов широкополосных хаотических сигналов. Такие генераторы с существенно нелинейной (N–образной) вольт-амперной характеристикой туннельного диода относятся к неравновесным динамическим системам, в которых наблюдается возбуждение неустойчивых хаотических колебаний [1, С. 4], [2, С. 7], [3, С. 217], [4, С. 3], [5, С. 385], [6, С. 18], [7, С. 355].
Для аналитического исследования работы генератора и возможных при этом динамических режимов используются методы теории неустойчивости развиваемых авторами в работах [8, С. 4], [9, С. 4], [10, С. 8], [11, С. 4].
Генератор предложен и изучен в экспериментальном режиме Кияшко C.В., Пиковским А.С., Рабиновичем М.И. [1, С. 4], [2, С. 8]. Электрическая схема генератора с нелинейной вольт-амперной характеристикой и аттрактор, отражающий динамику хаотических колебаний, приведены на рис 1,2.
Исходные динамические уравнения генератора имеют вид [2, С. 7], [7, С. 355].
![]() (1)
(1)
где I-ток в цепи, U-напряжение, V- напряжение в диоде, L- индуктивность, C- емкость цепи, c-емкость туннельного диода, (-R)- отрицательное сопротивление диода (коэффициент усиления), Im, Um-максимальные значения тока и напряжения. После введения безразмерных переменных
![]() (2)
(2)
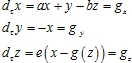 (3)
Где
(3)
Где 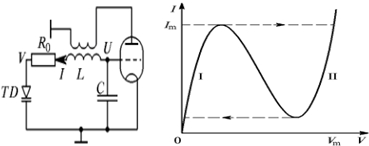
Рис. 1 – Схема и вольт-амперная характеристика электронного генератора с нелинейным туннельным диодом
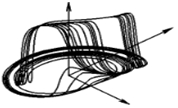
Рис. 2 – Фазовый портрет аттрактора в пространстве динамических переменных (x,y,z)
Итак, поставим задачу: получить условия неустойчивости и хаоса динамических режимов генератора, описываемых системой (3) в аналитическом виде через динамические коэффициенты (4) и согласовать их с наблюдаемыми.
Критериальный анализ процессов динамики в генераторе
Используем для анализа динамики системы (3) метод L-критерия и сингулярно- динамический (СД- метод) реализуемый следующей схемой (см.[2,c.7],[7,c.355]).
а) Сначала определяются особенности выражений описывающих модель. В нашем случае это особенности правых частей уравнений: нули, бесконечности, точки бифуркации, а также нули их производных и т.д. Например:
![]() (5)
(5)
Значения ![]() в этих точках соответственно равны 1 и 0,151, одна из этих точек соответствует максимуму другая минимуму функции g. Значения дивергенции вектора правых частей уравнений (3)
в этих точках соответственно равны 1 и 0,151, одна из этих точек соответствует максимуму другая минимуму функции g. Значения дивергенции вектора правых частей уравнений (3)
![]() (6)
(6)
указывает области роста и уменьшения фазового объема и является одним из условий устойчивости-неусточивости. В данном случае границы этих областей также являются особыми точками в спектре.
б) Далее рассматриваются стационарные точки (они же точки бифуркации по времени). Это нули правых частей, в данном случае равных
![]() (7)
(7)
Если вследствие нелинейности получается несколько стационарных точек, зависящих от параметров системы, то следует изучить и их особенности.
в) Критериями теории неустойчивости [8, С. 4], [9, С. 4], [10, С. 8], [11, С. 4] исследуется спектр линеаризированных уравнений исходной системы в стационарных точках и вблизи особенностей, а также определяются условия возможных неустойчивости и хаоса.
В общей теории неустойчивости наряду с указанными точками также рассматривается линеаризация около произвольных точек - начальных условий. В последнем случае изучается зависимость спектра и режимов неустойчивости и хаоса от начальных данных.
Метод L – критерия состоит получении условий нейтральности (границы устойчивости-неустойчивости) через коэффициенты динамических уравнений с помощью определителя блочной матрицы ![]() составленной из эволюционной матрицы
составленной из эволюционной матрицы ![]() и ее элементов. Формула L – критерия имеет общий вид [8, С .4], [10, С. 8].
и ее элементов. Формула L – критерия имеет общий вид [8, С .4], [10, С. 8].
![]() (8)
(8)
Где ![]() - эволюционная матрица,
- эволюционная матрица, ![]() -комплексно сопряженные элементы матрицы,
-комплексно сопряженные элементы матрицы, ![]() - единичная матрица, n-размерность системы,
- единичная матрица, n-размерность системы, ![]() - обобщенные собственные значения эволюционной матрицы (которые являются аналогом показателей Ляпунова и совпадают с ними в случае стационарных состояний).
- обобщенные собственные значения эволюционной матрицы (которые являются аналогом показателей Ляпунова и совпадают с ними в случае стационарных состояний).
Равенство нулю критерия (8) соответствует наличию нулевых производных (собственных значений), смена знака критерия – смене знака временных производных в динамических уравнениях. Таким образом, анализ множителей в (8) представляет собой анализ спектра собственных значений эволюционной матрицы нелинейной системы и, следовательно, анализ знаков временных производных в линеаризированных динамических уравнениях (3).
Итак, запишем линеаризированную систему в общем виде
![]() (9)
(9)
Коэффициенты s,p,q зависят от параметров точки линеаризации и выражаются через eik.
В частности,
![]()
Неустойчивость связана с наличием корней спектрального уравнения - (СУ) с положительной вещественной частью; хаос - с наличием колебаний и взаимодействием растущей и затухающей мод , т.е. наличием в спектре особой точки седло-фокуса. Тогда соотношения, определяющие границы областей неустойчивости и хаоса, имеет вид [9,c4], [11,c.4].
![]() (11)
(11)
Первое неравенство (11) есть условие неустойчивости, второе — достаточное условие колебаний, третье — седлообразный характер спектра. Критерии (11) становятся очевидными, если учесть связь их и коэффициентов СУ с собственными значениями, для СУ (10) равными
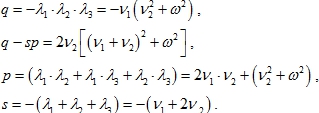
Где ![]() вещественный и комплексно-сопряженные корни СУ (10).
вещественный и комплексно-сопряженные корни СУ (10).
Для нелинейного генератора линеаризированная около произвольных состояний система (3) и соответствующая эволюционная матрица ![]() имеют вид
имеют вид
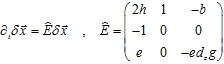 (12)
(12)
Первое из этих выражений есть условие нейтральности (границы устойчивости), второе есть условие наличия колебаний (существование частоты), третье- наличие в спектре точки седло-фокуса.
Например, в точках экстремума ![]() эти условия соответственно равны
эти условия соответственно равны
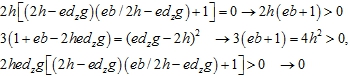 (15)
(15)
Из условий (15) следует наличие вблизи этих точек неустойчивых хаотических колебаний, что соответствует наблюдаемым в экспериментах с нелинейными генераторами неустойчивым хаотическим режимам [2,c.7],[7,c.355].
Применение L-критерия (8) для системы (12) дает выражение
![]() (16)
(16)
Из сравнения L-критерия (16) с условиями (14) следует, что он содержит в себе и условие нейтральности и условие седло-фокуса и указывает на возможность третьего критического режима- третий множитель в (16). Знаки трех множителей в (16) соответствуют знакам временных производных в динамической системе (12), а комбинация знаков говорит о возможности в генераторе неустойчивого хаотического режима.
Заключение
Рассматривается динамика возмущений в модели нелинейного электронного генератора
Кияшко C.В. Пиковского А.С., Рабиновича М.И. Для выявления эффектов неустойчивости и хаоса используется сингулярно-динамический метод и метод L-критерия теории неустойчивости развиваемой авторами. Получены аналитические условия неустойчивости, из которых следует, что в окрестности экстремумов вольтамперной характеристики в генераторе возбуждаются неустойчивые хаотические колебания в соответствии с наблюдаемыми в эксперименте режимами.
Результаты, полученные в настоящей работе, могут быть полезны как для дальнейших теоретических исследований динамических режимов в нелинейных генераторах, так и для оптимизации работы устройств использующих такие генераторы.
Список литературы / References
- Пиковский А.С., Рабинович М.И. Простой автогенератор со стохастическим поведением . / Пиковский А.С., Рабинович М.И //ДАН СССР.-1978.- т.23.- №2.-C. 301-304.
- Кияшко С.В., Пиковский А.С., Рабинович М.И. Автогенератор радиодиапазона со стохастическим поведением./ Кияшко С.В., Пиковский А.С., Рабинович М.И.// Радиотехника и электроника.- 1980.- т.25.- №2.-C. 336-343.
- ЗаславскийГ.М. Стохастичность динамических систем. / ЗаславскийГ.М.// М.Наука.- 1984.- C. 271.
- Дмитриев А.С., Кислов В.Я., Старков С.О. Экспериментальное исследование образования и взаимодействия странных аттракторов в кольцевых автогенераторах. //ЖТФ.-1985.-т.55.- №12.- C. 2417-2419.
- Ott E. Chaos in Dynamical Systems./ Ott E Cambridg Yniversity Press. // 1993.-C.385 .
- Анищенко В.С. Аттракторы динамических систем. / . Анищенко В.С. // Изв.Вузов, Прикладная нелинейная динамика.- 1997.- т.5.-№1.-C. 109-127.
- Кузнецов С.П. Динамический хаос. / Кузнецов С.П. // ФМ.- М. –Физматгиз.-2006.-C.355.
- Перевозников Е.Н. Критерий устойчивости нелинейных систем. /Перевозников Е.Н.// Изв.Вузов ,физика.-2013- №56.-C. 151-154.
- Скворцов Г.Е., Перевозников Е.Н. Сингулярно-динамические критерии неустойчивости и хаоса. / Скворцов Г.Е., Перевозников Е.Н. //Международный научно-исследовательский журнал, физико-математические науки.- - №9.-ч.3.-C.91-93.
- Perevoznikov, O. Mikhailova. Neutrality Criteria for Stability Analysis of Dynamical Systems through Lorentz and Rossler Model Problems. / E. Perevoznikov, O. Mikhailova. //Journal of Applied Mathematics and Physics- 2015.- №5.-C. 569-576.
- Скворцов Г.Е., Перевозников Е.Н. Теория неустойчивости и критерии хаоса / Скворцов Г.Е., Перевозников Е.Н.// Международный научно-исследовательский журнал, физико-математические науки.- 2016.-№7.- ч.4.-C.98-101.
Список литературы на английском языке / References in English
- Pikovsky A.S., Rabinovich M.I. Prostoy avtogenerator so stokhasticheskim povedeniyem [Simple Self-Oscillator with Stochastic Behavior] / Pikovsky A.S., Rabinovich M.I. // DAN USSR. – 1978. – Vol. 23 – No. 22 – P. 301-304. [In Russian]
- Kiyashko S.V., Pikovsky A.S., Rabinovich M.I. Avtogenerator radiodiapazona so stokhasticheskim povedeniyem [Autogenerator of Radio Range with Stochastic Behavior. / Kiyashko S.V., Pikovsky A.S., Rabinovich M.I. // Radio-engineering and electronics. – 1980. – V.25. – No.2. – P. 336-343. [In Russian]
- Zaslavsky G.M. Stokhastichnost' dinamicheskikh sistem [Stochasticity of Dynamical Systems] / Zaslavsky G.M./ M. Nauka. – 1984. – P. 271. [In Russian]
- Dmitriev A.S., Kislov V.Ya., Starkov S.O. Eksperimental'noye issledovaniye obrazovaniya i vzaimodeystviya strannykh attraktorov v kol'tsevykh avtogeneratorakh [Experimental Study of Formation and Interaction of Strange Attractors in Ring Autogenerators] // ZhTF. – 1985. – p.55. – No.12. – P. 2417-2419. [In Russian]
- Ott E. Chaos in Dynamical Systems./ Ott E Cambridg Yniversity // 1993.-C.385.
- Anishchenko V.S. Attraktory dinamicheskikh sistem [Attractors of Dynamic Systems] / Anischenko V.S. // Izv. Vuzov, Applied nonlinear dynamics. – 1997. – Vol.5. – No.1 – P. 109-127. [In Russian]
- Kuznetsov S.P. Dinamicheskiy khaos [Dynamic Chaos] / Kuznetsov S.P. // FM-M. – Fizmatgiz-2006. – P.355. [In Russian]
- Perevoznikov E.N. Kriteriy ustoychivosti nelineynykh sistem [Stability criterion of Nonlinear Systems] / Perevoznikov E.N. // Izv Vuzov, Physics. – 2013 – No.56. – P. 151-154. [In Russian]
- Skvortsov G.E., Perevoznikov E.N., Singulyarno-dinamicheskiye kriterii neustoychivosti i khaosa [Singular-Dynamic Criteria of Instability and Chaos] / Skvortsov G.E., Perevoznikov E.N. // International Scientific and Research Journal, Physics and Mathematics. – 2015. – No.9. – P.3. – P.91-93. [In Russian]
- Perevoznikov, O. Mikhailova. Neutrality Criteria for Stability Analysis of Dynamical Systems through Lorentz and Rossler Model Problems. / E. Perevoznikov, O. Mikhailova. // Journal of Applied Mathematics and Physics- 2015.-? 5.-C. 569-576.
- Skvortsov G.E., Perevoznikov E.N. Teoriya neustoychivosti i kriterii khaosa [Theory of Instability and Chaos Criteria] / Skvortsov G.E., Perevoznikov E.N., International Scientific and Research Journal, Physics and Mathematics. – 2016. – No.7. – P.4. – P. 98-101. [In Russian]
