ON A DETAILED DESIGN OF THE PROBLEM SOLUTION AS A FACTOR IN AVOIDING LOGICAL ERRORS

РАЗВЕРНУТОЕ ОФОРМЛЕНИЕ РЕШЕНИЯ ЗАДАЧИ КАК ФАКТОР НЕДОПУЩЕНИЯ ЛОГИЧЕСКИХ ОШИБОК

Научная статья

Костюченко Р.Ю.*

ORCID: 0000-0001-7763-0631,

Омский государственный педагогический университет, Омск, Россия

* Корреспондирующий автор (kryu[at]bk.ru)

Аннотация

В статье рассматривается вопрос культуры письменной математической речи при оформлении решения задач на доказательство. Автором показывается прямая связь между совершаемыми учащимися ошибками в доказательствах и неполным оформлением решения. Учащиеся, излагая доказательство в виде последовательности силлогизмов, часто опускают большую посылку, что влечет, по мнению автора, сокрытие возможной ошибки. В доказательство этого убедительно показывается, что развернутое оформление решения, а именно, явное выделение в каждом силлогизме большей посылки, меньшей посылки и вывода, будет способствовать видению учащимся потенциальных противоречий, недосказанности и, как следствие, недопущению возможных ошибок.

Ключевые слова: обучение математике, решение задачи, оформление решение задачи, оформление доказательства, ошибки в доказательстве.

ON A DETAILED DESIGN OF THE PROBLEM SOLUTION AS A FACTOR IN AVOIDING LOGICAL ERRORS

Research article

Kostyuchenko R.Yu.*

ORCID: 0000-0001-7763-0631,

Omsk State Pedagogical University, Omsk, Russia

* Корреспондирующий автор (kryu[at]bk.ru)

Abstract

The article deals with the issue of the culture of written mathematical speech in the design of the solution of proof problems The author directly links the mistakes made by students in the proofs with the incomplete written execution of the solution. While presenting the proof in the form of a sequence of syllogisms, students often omit a major premise, which, in the author's view, leads to concealing a possible error. In proof of this, it is convincingly shown that the detailed execution of the solution, namely, the explicit allocation of a major premise, a minor premise, and a conclusion in each syllogism will help students to see potential contradictions and understatements, thus avoiding possible mistakes.

Keywords: teaching mathematics, problem-solving, execution of solution, proof design, errors in the proof.

Введение

Во многих случаях необходимым этапом решения задачи является развернутое оформление её решения [5]. Это могут быть задачи и на вычисление, и на доказательство, которые могут встречаться как в классной, так и в домашней работах учеников, как в тренировочных, так и контрольных заданиях разного уровня. Наиболее отчетливо умение оформлять найденное решение проявляется в пробных и реальных вариантах итоговой аттестации учащихся в 9-ом и 11-ом классах соответственно на основном государственном экзамене (ОГЭ) и едином государственном экзамене (ЕГЭ). Так, автор статьи на протяжении нескольких лет является членом федеральной предметной комиссии по проверке работ ЕГЭ по математике, а также автором и экспертом по проверке пробных вариантов ОГЭ и ЕГЭ по математике. За это время нам встречались работы учащихся, которые можно назвать образцовыми, однако есть много работ с верным решением, но с существенными замечаниями по его изложению. Как ни странно, в последнее время одно из замечаний, казалось бы и не имеющего ничего общего с математической составляющей, касается аккуратности в письменном представлении решения. Так, встречаются не единичные работы, в которых эксперт был не в состоянии разобрать написанные учеником отдельные буквы, слова, обозначения. При этом страдает и общность ответа: нередки зачеркивания, перечеркивания, хаотичное расположение излагаемого материала. Усугубляется данная тенденция еще и тем, что снижение отметки за неаккуратность на итоговом экзамене по математике не происходит. Представляется, что устранение данного замечания должно решаться комплексно на межпредметном уровне. Однако вернемся к математической составляющей оформления решения задачи.

Вопросу обучения учащихся решению задач и связанным с этим методическим аспектам посвящены исследования многих ученых В.А. Далингера [2], Ю.М. Колягина [3], [4], Пойа Д. [7], Г.И. Саранцева [8], Л.М. Фридмана [9], [10] и других. Нас же сейчас в большей мере будет интересовать вопрос об ошибках, допускаемых учащимися в доказательных рассуждениях, и их возможной связи с оформлением решения.

Основные результаты

Рассмотрим задачу на доказательство, предложенную в пробном тестировании учащимся 9-го класса.

Задача 1. В треугольнике АВС отрезок BM является и биссектрисой, и медианой (рис. 1). Докажите, что ВМ – высота треугольника АВС.

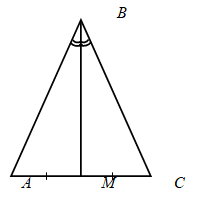
Рис. 1 – Чертеж к задаче 1: ∆АВС, BM – биссектриса и медиана

 

Практически во всех работах встречается одна и та же ошибка: в процессе решения учащиеся обосновывают равенство треугольников АВМ и СВМ несуществующей теоремой (ссылаясь по ошибке на первый признак равенства треугольников). Ученики пишут так: «АМ=МС, АВМ=СВМ, ВМ – общая, следовательно ∆АВМ=∆СВМ».

Поясним суть ошибки и её возможное предупреждение.

В указанном предложении вначале обозначена меньшая посылка, далее указывается вывод, а бóльшая посылка (обосновывающая теорема) отсутствует. Вот здесь то и проблема, что нет обосновывающей теоремы. Нет теоремы – не в том плане, что её не указали, а в том, что теоретически не существует предполагаемой обосновывающей теоремы. Учащиеся, вероятно, хотят использовать первый признак равенства треугольников, но в этом признаке, как помним, равные углы должны располагаться между соответственно равными сторонами, а в нашем случае такого не наблюдается, поэтому использовать первый признак равенства треугольников в данном случае нельзя.

Можно недоверчивым учениками привести контрпример (рис. 2). От луча ВМ в обе стороны отложим по равному углу так, чтобы они пересекали некоторую окружность с центром в точке М. Тогда АМ=МС=R, АВМ=СВМ (по построению), ВМ – общая, но треугольники АВМ и СВМ, как очевидно, не равны.

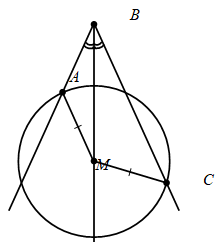
Рис. 2 – Контрпример к задаче 1: ∆АВM и ∆СВМ не равны

Как же увидеть ученику ошибку? Как её не допустить?

Нам представляется, если ученик в оформлении решения задачи в каждом силлогизме будет выделять меньшую посылку, вывод, а также и большую посылку как обосновывающий фактор, то подобных ошибок можно будет избежать. Действительно, если в представленном примере осознанно сослаться на первый признак равенства треугольников, то можно будет увидеть, что в представленных данных условия теоремы не выполняются.

Рассмотрим еще один пример.

Задача 2. В четырехугольнике ABCD известно, что AB=AD и BC=CD (рис. 3). Докажите, что диагонали АС и BD, перпендикулярны.

 

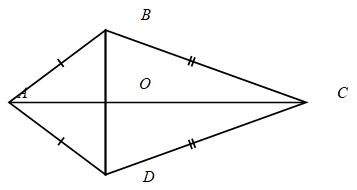
Рис. 3 – Чертеж к задаче 2: ABCD – четырёхугольник, AB=AD и BC=CD

Ошибочное суждение: «Пусть диагонали пересекаются в точке О. Так как треугольник АВD – равнобедренный, то АО в нем является и биссектрисой, и медианой, и высотой». Да, действительно, в соответствии со всеми условиями задачи отрезок АО в равнобедренном треугольнике АВD будет являться и биссектрисой, и медианой, и высотой, но обоснование этому какое? Нет такой теоремы, в которой говорится, что в равнобедренном треугольнике отрезок, соединяющий вершину с некоторой точкой основания, является и биссектрисой, и медианой, и высотой.

Здесь должна быть ссылка на теорему: «В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой» [1, С. 35] – это в силлогизме большая посылка. Меньшая посылка будет: «∆АВD – равнобедренный, АО – биссектриса, BD – основание». Вывод: «ОА – медиана и высота». Понятно, что предварительно требуется показать, что ОА – биссектриса (это следует из равенства треугольников АВС и АDС по трём сторонам).

Как видим, в данном примере, как и в предыдущем, в изложении доказательства опущена большая посылка. Аналогично, нам представляется, если ученик будет явно указывать конкретные данные (меньшую посылку) и обосновывающую вывод теорему (большую посылку), то придет к очевидному противоречию: исходных в условии задачи данных, о которых говорится в теореме, не хватает. Следовательно, казалось бы, очевидный вывод не обоснован и не может быть использован в решении.

Представим пример, в котором рассматривается стереометрический факт.

Задача 3. В правильной шестиугольной пирамиде SABCDEF отрезок SO – её высота, SM – апофема боковой грани SCD. Докажите, если OH перпендикуляр к SM, то OH является перпендикуляром к плоскости SCD.

Ошибочное доказательство во многих случаях сводится к следующей последовательности суждений: «Поскольку OH перпендикуляр к SM, а SM принадлежит к плоскости SCD, то OH является перпендикуляром к плоскости SCD». Это неверно. Для доказательства учащиеся используют несуществующий (ложный) признак перпендикулярности прямой и плоскости, суть которого представляют так: «Если прямая а перпендикулярна прямой b, лежащей в плоскости α, то прямая а перпендикулярна плоскости α». Ложность данного высказывания легко показать контрпримером. Для этого из наглядных средств эксперт использовал обычную швабру: ручка – прямая а, основание – прямая b, пол – плоскость α. Ставим швабру ручкой перпендикулярно полу – все условия мнимого признака выполняются. Далее, оставляя основание швабры на полу, наклоняем ручку – условия в посылке мнимого признака также выполняются, но заключение – нет, что очевидно. Будем размышлять далее – как заставить швабру быть перпендикулярной полу? Можно ли в жизни найти подобный пример? Да, можно – ёлка на крестовине – натуральный пример истинного признака перпендикулярности прямой и плоскости: «Если прямая a перпендикулярна двум пересекающимся прямым b и c, лежащим в плоскости α, то она перпендикулярна этой плоскости α» [6, С. 38]. Замечу, что такой пример будет содержать несущественные свойства признака – перпендикулярность двух прямых b и c, лежащих в плоскости (достаточно их пересечения), а также наличие общей точки у трех прямых (необязательно чтобы прямая a проходила через точку пересечения двух прямых b и c).

В представленном примере ошибочно в качестве большей посылки используется определение перпендикулярности прямой и плоскости. Но в определении то говорится о любой прямой, лежащей в плоскости, а в указанном доказательстве рассматривается конкретная прямая. Перпендикулярность чаще всего должна обосновываться признаком перпендикулярности прямой и плоскости. Ошибка в примере состоит в подмене и неверном использовании большей посылки. Эту посылку следовало указать во избежание неверного вывода.

Заключение

Подытоживая сказанное, отметим, что при письменном оформлении доказательства в виде последовательности силлогизмов следует каждый силлогизм приводить полностью, явно выделяя три его части: большую посылку, меньшую посылку и вывод. Это будет способствовать видению учащимся потенциальных противоречий, недосказанности в решении и, как следствие, недопущению возможных ошибок.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Геометрия. 7-9 классы: учебник для общеобразовательных организаций / Л.С.Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 11-е изд. – М.: Просвещение, 2020. – 383 с.
2. ДалингерВ.А. Методика обучения математике. Обучение учащихся доказательству теорем: учебное пособие для вузов / В.А. Далингер. – 2-е изд., испр. и доп. – М.: Юрайт, 2020. – 338 с.
3. КолягинЮ.М. Задачи в обучении математике. В 2-х частях: Ч. 1. Математические задачи как средство обучения и развития учащихся / Ю.М. Колягин. – М.: Просвещение, 1977. – 112 с.
4. КолягинЮ.М. Задачи в обучении математике. В 2-х частях: Ч. 2. Обучение математике через задачи и обучение решению задач / Ю.М. Колягин. – М.: Просвещение, 1977. – 144 с.
5. КостюченкоР.Ю. Методика обучения учащихся решению математических задач: содержание этапов решения / Р.Ю. Костюченко // Вестник Сибирского института бизнеса и информационных технологий. – 2018. – № 4 (28). – С. 117-123.
6. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10-11 классы: учебник для общеобразовательных организаций: базовый и углубленный уровни / Л.С. Атанасян и др. – 7-е изд., перераб. и доп. – М.: Просвещение, 2019. – 287 с.
7. Пойа Д. Как решать задачу / Д. Пойа. – М.: Учпедгиз, 1959. – 208 с.
8. СаранцевГ.И. Обучение математическим доказательствам и опровержениям в школе: книга для учителя / Г.И. Саранцев. – М.: Владос, 2006. – 183 с.
9. ФридманЛ.М. Как научиться решать задачи: пособие для учащихся / Л.М. Фридман, Е.Н. Турецкий. – М.: Просвещение, 1984. – 175 с.
10. ФридманЛ.М. Теоретические основы методики обучения математике: учебное пособие / Л.М. Фридман. – 2-е изд., испр. и доп. – М.: УРСС, 2005. – 244 с.

Список литературы на английском языке / References in English

1. Geometrija. 7-9 klassy: uchebnik dlja obshheobrazovatel'nyh organizacij [Geometry. 7-9 grades: textbook for educational organizations] / L.S. Atanasjan, V.F. Butuzov, S.B. Kadomcev et al. – 11nd edition. – M.: Prosveshhenie, 2020. – 383 p. [in Russian]
2. Dalinger V.A. Metodika obuchenija matematike. Obuchenie uchashhihsja dokazatel'stvu teorem: uchebnoe posobie dlja vuzov [Methodology of teaching mathematics. Teaching students to prove theorems: textbook for universities] / V.A. Dalinger. – 2nd edition, corrected and updated. – M.: Jurajt, 2020. – 338 p. [in Russian]
3. Koljagin Ju.M. Zadachi v obuchenii matematike. V 2-h chastjah: Ch. 1. Matematicheskie zadachi kak sredstvo obuchenija i razvitija uchashhihsja [Problems in teaching mathematics. In 3 h the P. 1. Mathematical problems as a means of teaching and developing students] / Ju.M. Koljagin. – M.: Prosveshhenie, 1977. – 112 p. [in Russian]
4. Koljagin Ju.M. Zadachi v obuchenii matematike. V 2-h chastjah: Ch. 2. Obuchenie matematike cherez zadachi i obuchenie resheniju zadach [Problems in teaching mathematics. In 3 h the P. 2. Teaching mathematics through problems and teaching problem solving] / Ju.M. Koljagin. – M.: Prosveshhenie, 1977. – 144 p. [in Russian]
5. Kostjuchenko R.Ju. Metodika obuchenija uchashhihsja resheniju matematicheskih zadach: soderzhanie jetapov reshenija [Methodology of teaching students of solving mathematical problems: solution steps and their content] / R.Ju. Kostjuchenko // Vestnik SIBITa [Bulletin of the Siberian Institute of Business and Information Technologies]. – 2018. – № 4 (28). – P. 117-123. [in Russian]
6. Matematika: algebra i nachala matematicheskogo analiza, geometrija. Geometrija. 10-11 klassy: uchebnik dlja obshheobrazovatel'nyh organizacij: bazovyj i uglublennyj urovni [Mathematics: algebra and the beginnings of mathematical analysis, geometry. Geometry. 10-11 grades: textbook for educational organizations: basic and advanced levels] / L.S. Atanasjan and others. – 7nd edition, corrected and updated. – M.: Prosveshhenie, 2019. – 287 p. [in Russian]
7. Poja D. Kak reshat' zadachu [How to solve a problem] / D. Poja. – M.: Uchpedgiz, 1959. – 208 p. [in Russian]
8. Sarancev G.I. Obuchenie matematicheskim dokazatel'stvam i oproverzhenijam v shkole: kniga dlja uchitelja [Teaching mathematical proofs and refutations in school: book for teachers] / G.I. Sarancev. – M.: Vlados, 2006. – 183 p. [in Russian]
9. Fridman L.M. Kak nauchit'sja reshat' zadachi: posobie dlja uchashhihsja [How to learn to solve problems: manual for students] / L.M. Fridman, E.N. Tureckij. – M.: Prosveshhenie, 1984. – 175 p. [in Russian]
10. Fridman L.M. Teoreticheskie osnovy metodiki obuchenija matematike: uchebnoe posobie [Theoretical foundations of the methodology of teaching mathematics: textbook] / L.M. Fridman. – 2nd edition, corrected and updated. – M.: URSS, 2005. – 244 p. [in Russian]