STATISTICAL STUDY EVALUATION OF CORRELATION BETWEEN ORGANIC COATING THICKNESS AND THREE HARDNESS TEST METHODS

Алимам Х.¹, Хиннави М.², Альзаин Х.³

¹ ORCID: 0000-0003-4744-6934, Ассистент преподавателя; ² Доцент, Кандидат технических наук; ³ Аспирант, Факультет Инженерии и Дизайна, Университет Дамаска

СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ОЦЕНКИ ТОЛЩИНЫ ОРГАНИЧЕСКОГО ПОКРЫТИЯ И ЕГО УСТОЙЧИВОСТИ В ТРЕХ ТЕСТАХ НА ТВЕРДОСТЬ

Аннотация

Целью исследования являлось определение прочности толщины покрытия, которое используется в защитном слое из полиэстера в алюминиевой катушке. Было использовано 120 образцов с алюминиевой подложной, покрытых полиэстером. Они включали 6 группы с разной толщиной покрытия (1 группа = 73 мкм), (2 группа = 81 мкм), (3 группа = 120 мкм), (4 группа = 150 мкм), (5 группа = 180 мкм) и (6 группа = 210 мкм) из каждой группы было использовано 20 образцов. Прочность была исследована на основании следующих свойств: вдавливание, демпфирование, устойчивость к царапинам; кроме того, была изучена взаимосвязь с толщиной покрытия. Статистические анализы, такие как дисперсионный анализ, тест Крускала-Уоллиса, и испытание по двумерному критерию, были использованы для сравнения среднего показателя зависимости прочности от толщины. В результате исследования была выявлена связь между прочностью (такими ее вдавливание и демпфирование) и толщиной покрытия из полиэстера.

 Ключевые слова: органическое покрытие, метод Кноопа, дисперсионный анализ, испытание по двумерному критерию, прочность маятника.

 

Alimam H.¹, Hinnawi M.², Alzain Kh.³

¹ORCID: 0000-0003-4744-6934, Teaching Assistant, Mechanical Design Engineering at Damascus University, ² Assistant Professor, PhD in Mechanical Design Engineering , Damascus University, ³ Postgraduate Student, Mechanical Design Engineering at Damascus University

STATISTICAL STUDY EVALUATION OF CORRELATION BETWEEN ORGANIC COATING THICKNESS AND THREE HARDNESS TEST METHODS

Abstract

This study is carried out for determining the effect of coating thickness on Hardness which is used on the protective layer when polyester coating is applied on the aluminum coil. Total 120 samples with aluminum substrate and coated with polyester coating were used for Hardness test. For coating thickness six group were made (Group 1 = 73 μm), (Group 2 = 81μm), (Group 3 = 120 μm), (Group 4 = 150 μm), (Group 5 = 180 μm) and (Group 6 = 210μm), for each group Twenty samples were used. Hardness was investigated by using three methods: indentation hardness, damping hardness, and Scratch hardness; in addition we investigated their relationship and the effect of the coating thickness. Statistical analysis (ANOVA Test, Kruskal-Wallis Test& Bivariate Correlate Test) were used to compare mean effect of different thickness on Hardness, and to evaluate correlation between coating thickness and Hardness. According to the result of the study, an excellent correlation between Hardness (indentation hardness, damping hardness) and thickness of polyester coatings is obtained, which is fairly supported by the experimental and statistical data.

Keywords: Organic coating, Knoop micro hardness, ANOVA Test, Bivariate correlate, Pendulum hardness.

INTRODUCTION:

Coating technology was used for protection and acquisition painted aesthetic elements, so many of the industrial products are painted using organic and inorganic materials, to give these products long-term protection under a wide range of causing wear conditions and erosion during the functional age of these Products [1].

 Organic coatings are widely applied in many fields, such as in the automotive industry, coil coating used in construction, furniture, ships, containers, and children’s toys, for the protection and decoration of substrates [2, 3]. There are many paint systems used in coating which we can highlight, polyamide and Polyurethane (PA \ PU) coating, Acrylic Coating, polyester Coating and Epoxy Coatings, which constitute the most important types of organic coatings used to protect the structure and improve the mechanical properties such as resistance to scratching, wear resistance, hardness and durability [4]. American Society for Testing and Materials ASTM advises to use certain tests to ensure the quality of the characteristics for coated metal sheet. These tests are performed according to a specific standards like;  bending test ASTM D4145, impact test ASTM D6905, scratch resistance test ASTM D7027, dry & wet adhesion test ASTM D2197, micro hardness test D1474, abrasion resistance test ASTM D4060, and chemical resistance test ASTM D1308 [1, 5].

Hardness is one of the most important properties of organic coatings, and is commonly used to estimate the mechanical properties of coatings. Although numerous methods have been developed to determine coating’s hardness, pendulum hardness and micro hardness tests are the most widely used ones in laboratory research because of their higher accuracy than common methods used in industry such as pencil hardness and nail hardness [6]. Until now, there is no generally recognized method for the quantification of the scratch resistance or surface damage of polymers. Analogous to the indentation hardness, Williams [7] proposed the definition of scratch hardness to characterize the scratch resistance of metals. Other parameters such as tangential hardness, dynamic hardness and specific grooving energy were considered by various authors [8, 9].

Browning et al, [10] have proved in their research where they evaluate the scratch resistance of the polymeric coating, that the low thickness of the coating, will have double effect for each of the substrate and layer of paint on the micro hardness and the scratching hardness as a result of a complex relationship generated between the stresses of both materials. It has been a well-known fact that micro hardness depends greatly on the relative indentation depth (RID, the ratio of indentation depth to thickness of coating) Many models have been proposed to describe the relationship between micro hardness and the RID, which are mainly based on the principle that the measured values of micro hardness are representative of coating/substrate composite hardness [11, 12].  However, the influenced of thickness of coating on pendulum hardness has not attracted much attention, although pendulum hardness values are generally compared at the same thickness of coating, [13, 14].

Xiao Yang Ma et al. [15] found that the pendulum hardness of acrylic coatings decreases gradually with the increasing thickness of coating within a thickness range, and the sensitivity of pendulum hardness to thickness of coating depends greatly on the glass transition temperature of the coatings.

Hwang et al. [16] studied the pendulum hardness of coatings on different wood substrates and found that the pendulum hardness varies with different kinds of substrates and coatings.

Both Choi & Kim [6], have proved in their research, which have follow three methodologies to evaluate the hardness of epoxy Acrylate coatings. The hardness values ​​are affected by the hardness of the coated material where it was noted that the hard substrate resulting in little coating layer hardness, as well the sensitivity of the tests for hardness of the surface of the paint film tracing the following order: micro hardness – pendulum hardness – scratching hardness using a pencil.

In this study, we investigated the hardness Polyester coating (film) applied to the aluminum sheet (substrate) using the three methods: indentation hardness, damping hardness, and scratch hardness; there we also investigated relationship and the effect of the thickness of coating.

MATERIALS AND METHODS:

Research materials:

In this paper, we used samples of aluminum sheets (substrate) manufactured from the alloy (Aluminum Sheet 6061 T651), where the chemical composition within the permissible limits is depending on the standard specification (ASTM B209) [17]. The sheets were coated with a layer of polyester (coating film) with different thicknesses. The tested samples were obtained from a specialized factory for aluminum coil coating. Samples of aluminum sheet, thickness of 0.25mm and the dimensions (100 X100 mm). A commercial polyester powder coating (TGIC free and glossy type – RAL 6012) [18] was applied by electrostatic spray on the test samples mounted on proper holders, taking care of producing uniform deposition of the powder. Since the properties of a powder coating can vary considerably with its thickness, the test samples were produced with three different thicknesses (low thickness 73, 81 μm, mid thickness120, 150 μm & high thickness180, 210 μm) and at a rate of 29 samples of each thickness.

Test method:

Determination of Indentation hardness:

The micro hardness test was performed on coated samples by the micro hardness tester (Zeiss Axioskop 40 Micro Hardness Tester MHT 10) (Fig. 1), where this device is available with a Knoop indenter, rhombic-based pyramidal shaped diamond indenter. This indenter has been using during the test and that degree lab temperature during test execution. ASTM D-1474 [19, 20] deal with standard test methods for indentation hardness of organic coating when applied to a plane rigid surface.

Fig. 1 – Zeiss Axioskop 40 Micro Hardness Tester MHT 10

The apparatus was pre-set to apply a Knoop indentation with a 25 g load for 18 seconds normally to the surface to be measured. The length of the long diagonal of the impression was determined by means of a semiautomatic measuring system. The procedure was repeated in five widely spaced locations for each test sample and the results were expressed as the mean value.

Determining the scratch hardness using Hardness pencils test according to Wolff-Willborn “ASTM D3363”:

The purpose of the pencil test is to determine the hardness of an organic coating referring to the hardness scale of the pencil leads. To determine pencil hardness there are17 different pencils with harnesses’ from 6B to 9H For hardness testing the pencils, starting with 6B are moved over the coating with an appropriate device at a constant weight and at an angle of 30 – 45°. This practice, usually performed manually, is useful in production control testing but the results obtained may vary between different operators [19, 21]. To obtain more accurate measurements the tests were performed using a mechanical device that allows reproducing the fundamental test conditions (load of 750±10 g and pencil inclined at an angle of 45±1°). In terms of  “the hardest pencil which does not mark the coating”.

Determining the Damping hardness:

A König pendulum hardness tester (PH-5858 Pendulum hardness Tester with König pendulum, BYK-Gardner instruments GmbH) was used to monitor the surface hardness (pendulum hardness values) of polyester coatings with different thicknesses the pendulum hardness of the polyester was measured with respect to the pendulum oscillation time from 6° to 3°at 23 ± 1C°and 50±2 % R.H., The pendulum hardness test is based on the principle that the harder a measured surface, the greater the amplitude time of pendulum oscillation (ASTM D 4366) [22]. In this study, the pendulum’s oscillation time was measured by the count of the pendulum’s oscillations with an electronic counter. The number of oscillations for the amplitude to decrease from 6° to 3° was determined to be the König hardness.

STATISTIC METHOD:

Determining Sample Size from a Given Population:

To obtain the required sample size (120 samples) from total amount of the sample (given population 174), Krejcie and Morgan [23] table was used to determine the samples size of which will be subject to statistical analysis. For coating thickness six groups were made (Group 1 = 73 μm), (Group 2 = 81μm), (Group 3 = 120 μm), (Group 4 = 150 μm), (Group 5 = 180 μm) and (Group 6 = 210μm), Twenty samples were used for each group.

Statistical analysis:

For statistical analysis the mean effect of different thickness on micro hardness and pendulum hardness (Scale variables) were compared by using one way ANOVA (parametric analysis of variances), for homogeneity of variances levene’s test was employed at 0.05 significance level and for significant effect parametric Post Hoc Tukey type was employed at 0.05 significance level [24, 25]. Also the mean effect of different thickness group on pencil hardness (ordinal data) was compared by using Kruskal-Wallis test (Nonparametric test) [24]. This test was used on SPSS 17.0. The relationship between thickness Variables and hardness variables was described by using Correlation test. Bivariate Correlate test was used to determine the degree of correlation between the variable of coating thickness and variables of hardness (micro hardness and pendulum hardness). The strength of the correlation was measured by using correlation coefficient (Pearson’s Correlation r) at statistical significance level 0.01. The strength correlation between the group of thickness and variable of pencil hardness (ordinal data) was measured by using Spearman’s rank correlation coefficient rs at statistical significance level 0.01 [24, 26]. Regression test was employed to study the mathematical model which describes the correlation between the thickness variables and hardness variables [25].

RESULTS AND DISCUSSION:

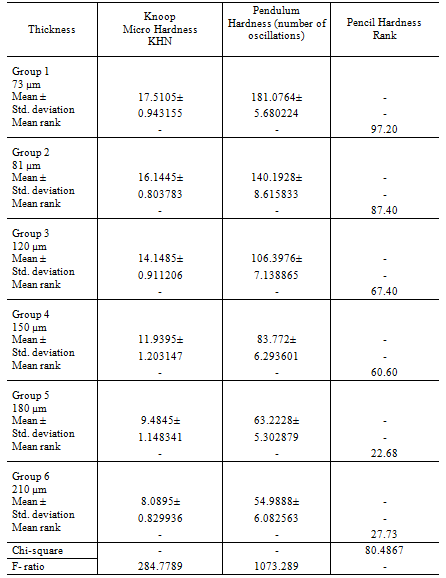
Pendulum hardness, Knoop micro hardness and Pencil hardness are summarized in Table 1. For pendulum hardness There was statistically significant difference in between all groups, F (5,114) =1073.289, (P < 0.05). Also levene’s test for homogeneity of variances is not significant (P=0.06 > 0.05) therefore the population variances for each group of pendulum hardness are approximately equal.

Pendulum hardness was the highest in group 1 at 73 μm of coating thickness, followed by the group 2, group 3, group 4, group 5 and group 6. The lowest pendulum hardness was found in group 6 at 210 μm of coating thickness.

 For Knoop micro hardness, there was statistically significant difference in between groups all groups, F (5,114) =284.779, (P < 0.05). Also levene’s test for homogeneity of variances is not significant (P=0.775 > 0.05) therefore the population variances for each group of micro hardness are approximately equal.  Micro hardness was the highest in group 1 at 73 μm of coating thickness, followed by the group 2, group 3, group 4, group 5 and group 6. The lowest Micro hardness was found in group 6 at 210 μm of coating thickness.

Table 1 – A summary of results; numbers in each group being 20.

The result of the Kruskal-Wallis test indicate that pencil hardness values significantly differ across the thickness groups, X² (5, N= 120) = 80.487, P<0.05. According to mean rank, pencil hardness rank was the highest in group 1 at 73 μm of coating thickness, followed by the group 2, group 3, group 4, group 5 and group 6. The lowest pencil hardness was found in group 6 at 210 μm of coating thickness.

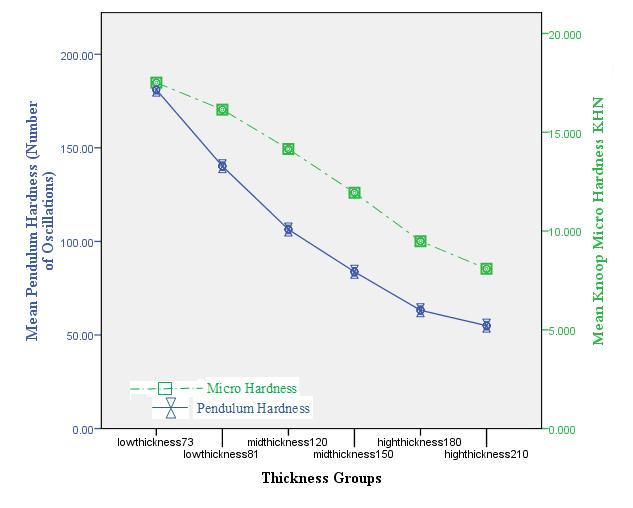
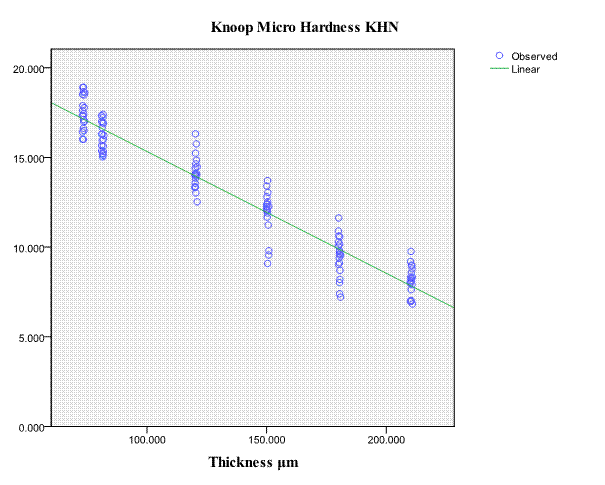
The results of experimental tests (pendulum hardness, micro hardness and coating Thickness tests), was illustrated in Fig. 2, which indicates the relationship between coating thickness and mean values ​​of  hardness for this coating according to the groups of studied samples. Fig. 3 shows the graphic representation of the micro hardness values and coating thickness values which uses scatter plot [21], which shows form a data flows in a straight line, a negative trend, indicating that the linear relationship between the two variables.

Fig. 2 – relationship between coating thickness and mean values ​​of hardness for this coating according to the groups of studied samples

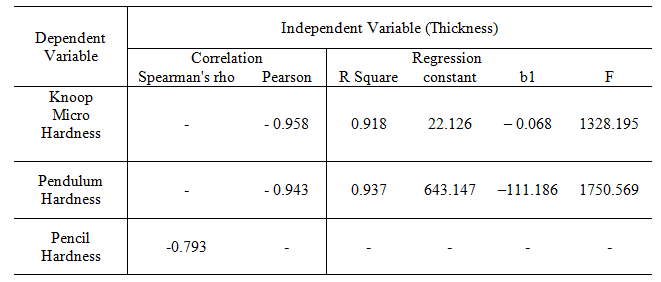
This relationship has been studied through the correlate test (Bivariate Correlate Test); the strength of this relationship was obtained from the Table 2. This table confirms the result of the scatter plot in that a significant negative relationship exists between micro hardness and coating thickness, test scours were strongly correlate (r(118)= - .958, P< 0.01). Thus higher micro hardness numbers are associated with lower coating thickness. Regression describes mathematical model between micro hardness and coating thickness. The result of regression is an equation that represents the best prediction of micro hardness number form coating thickness. Coating thickness explains 91.8 percent of the variance in micro hardness number, which is highly significant as indicated by F value of Table 1. The liner regression equation was "micro hardness = 22.126 – 0.068 * coating thickness, R² = .918, F (1, 118) = 1328.195, p< 0.01".

Table 2 –Regression & Correlation factors.

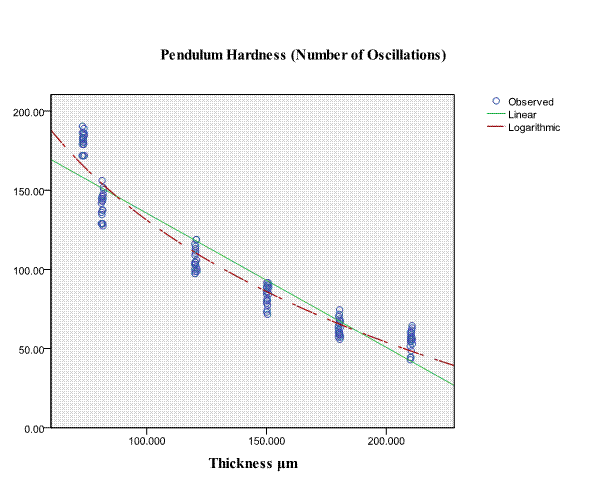
For pendulum hardness the relationship between coating thickness and mean values ​​of the pendulum hardness for this coating was illustrated in Fig. 2. Scatter Plot Fig. 4 was used to identify non liner regression between pendulum hardness number and coating thickness number, and this shows non liner regression and negative trend. The strength of this relationship was obtained from Table 2. This table confirms the result of the scatter plot in that a significant negative relationship exists between pendulum hardness and coating thickness and test scours were strongly correlate (r(118)= - .943, P<0 .01). Thus higher pendulum hardness numbers are associated with lower coating thickness.

Curve estimation test describes non liner regression model between Pendulum hardness and coating thickness. Logarithmic model was found between Pendulum hardness variables and coating thickness variables, the result of regression is an equation that represents the best prediction of Pendulum hardness number form coating thickness.

Fig. 3 –Micro hardness values & Coating thickness values which use Scatter Plot

Coating thickness explains 93.7 percent of the variance in pendulum hardness number, which is highly significant as indicated by F value of table 2. The non liner regression equation logarithmic model was "Pendulum hardness = 643.147 – 111.186 * Log (coating thickness), R² = .937, F (1, 118) = 1750.569, p< 0.01".

Fig. 4 –Pendulum hardness values & Coating thickness values which use Scatter Plot

A good relationship was found between Pencil hardness and coating thickness groups by using Non parametric correlation coefficient (Spearman rho), we can see from table 2 that Spearman’s rank order negative correlation is significant, rs (120) = -.793, P< 0.01, and so we can conclude that higher pencil hardness ranks are associated with lower coating thickness groups.

Conclusions:

To focus the attention on the results of hardness of coating, which has been obtained using three methods, it was noted the following:

Micro hardness of polyester coating was significantly affected by the thickness of the coating layer, where the values of micro hardness have high sensitivity to the values of the coating layer thickness.

For the range of the thickness of the layers of coating from the value 73μm as low thickness to the value 210μm as high thickness, the coating layers show variable resistance for the penetration of Knoop indenter. It was observed from the values of the micro hardness obtained from the experimental tests for the coating layer that the coating layer with low thickness has micro hardness equal 17.5KH and this value gradually decreases with increasing thickness of the coating layer up to the value 8.08KH.

 The relationship between micro hardness (KHN) and the thickness (S) of the polyester coating layer can be described by the following mathematical model representing of liner regression:

Pendulum hardness is greatly influenced by coating thickness, The relationship between pendulum hardness (PHN) and thickness of coatings (S) can be described by equation   with high accuracy within a certain range of thickness of coating, i.e., from 73 to 210 µm.

Coating thickness has a significant effect on Pencil hardness rank; the statistic analyses show that good correlation between coating thickness groups and pencil hardness ranks. Low thickness group has high Pencil hardness rank 2H, 3H and this ranks gradually decreases with increasing thickness up to the rank F, HB, B.

References

1. Koleske V. Mechanical Properties of Solid Coatings // Encyclopedia of Analytical Chemistry. –2001. - № 5. – P. 30-45.
2. R. Holman U.V, Curing E B. Formulation for Printing Inks, Coatings and Paints // Selective Industrial Training Associates Limited, London U.K, –1984. – P.7-18.
3. Sander J. Coil Coating // Vincentz Network, Hanover, Germany, 2014. P. 178.
4. ASIF ALAM, M. Fabrication of Various Epoxy Coatings for Offshore Applications and Evaluating Their Mechanical Properties and Corrosion Behavior // Int. J. Electrochem. Sci. –2013. - № 8. – P. 3121 – 3131.
5. ASTM D3794-13. Standard Guide for Testing Coil Coatings in Annual Book of ASTM Standards // ASTM International West Conshohocken PA. – 2013. - № 06.02.
6. Choi J. H., Kim H. J. Three Hardness Test Methods and Their Relationship on UV-Curable Epoxy Acrylate Coatings for Wooden Flooring Systems // J. Ind. Eng. Chem. – 2006. - № 12 (3). – P. 412–417.
7. Williams J.A. Analytical models of scratch hardness // Tribol. Int. – 1996. - № 29 (8). – P. 675–694.
8. Briscoe B.J., Delfino A., Pelillo E. Single-pass pendulum scratching Of poly (styrene) and poly (methylmethacrylate) // Wear. – 1999. - № 1. – P. 319–328.

9. Liang Y.N., S.Z. Li, D.F. Li, S. Li. Some developments for single-pass Pendulum scratching // Wear. – 1996. - № 199. – P. 66–73.
10. Browning R.L. Quantitative evaluation of scratch resistance of polymeric coatings based on a standardized progressive load scratch test // Surface & Coatings Technology. – 2006. - № 201. – P. 2970–2976.
11. Chen J., Bull S.J. On the Factors Affecting the Critical Indenter Penetration for Measurement of Coating Hardness // Vacuum. – 2009. - № 83 (6). – P. 911–920.
12. Wei P.J., Lin J.F. Anew Method Developed to Evaluate both the Hardness and Elastic Modulus of a Coating-Substrate System // Surf. Coat. Technol. – 2005. - № 200 (7). – P. 2489–2496.
13. Dashtizadeh A., Abdouss M., Mahdavi H., Khorassani M. Acrylic Coatings Exhibiting Improved Hardness, Solvent Resistance and Glossiness by Using Silica Nano Composites // Appl. Surf. Sci. – 2011. - № 257 (6). – P. 2118–2125.
14. Kivit P.J.J., Aramendia E., Cabrera A.A., Rios L.M. Water-Based Coatings Based on Mixtures of Acrylic Dispersions and Alkyd Emulsions // Macromol. Symp. – 2009. - № 283–284 (1). – P. 290–299.
15. Xiaoyang M.a., Zemin Q., Zhifeng H., Xinli J. The dependence of pendulum hardness on the thickness of acrylic coating // J. Coat. Technol. Res. – 2013. - № 10 (3). – P. 433–439.
16. Hwang H.D., Lee B.H., Choi J.H., Kim H.J., Chung W.Y. Acoustic Property and Hardness of Coatings for Musical Instruments with Various Coating Thicknesses // Mokchae Konghak. – 2006. - № 34 (2). – P.58–67.
17. ASTM B209-14. Standard Specification for Aluminum and Aluminum-Alloy Sheet and Plate in Annual Book of ASTM Standards // ASTM International West Conshohocken PA. – 2014. - № 02.02.
18. Goldschmidt A., Streitberger H.J. BASF Handbook on Basics of Coating Technology 2nd revised edition // Vincentz Network Hannover Germany, 2007. P. 791.
19. Sward G., Koleske J.V. Paint and coating testing manual 15th edition of the Gardner-Sward handbook // ASTM International West Conshohocken PA. – 2012. P. 1026.
20. ASTM D1474. Standard Test Methods for Indentation Hardness of Organic Coatings in Annual Book of ASTM Standards // ASTM International West Conshohocken PA. – 2013. - № 06.01.
21. Barbato B., Ragazzini R. Determination of micro-indentation hardness of organic coatings // VDI Berichte. – 2002. - № 1685.
22. ASTM D 4366-95. Standard Test Methods for Hardness of Organic Coatings by Pendulum Test. Standards // ASTM International West Conshohocken PA. – 1984. - № 95.
23. Krejcie R.V., Morgan D.W. Determining Sample Size for Research Activities // Educational and Psychological Measurement. – 1970. - № 30. – P. 607-610.
24. Coakes S.J., Steed L., Ong C. SPSS analysis without anguish: version 17.0 for windows // Wiley Milton Qld, 2010. P. 289.
25. Sabine L., Brian S. E. A Handbook of Statistical Analyses Using SPSS // Chapman& Hall CRC, 2004. P.366.
26. Hauke J., Kossowski T. Comparison of values of Pearson’s and Spearman’s correlation coefficients on the same sets of data // Quaestiones Geographicae. – 2011. - № 30 (2). – P. 87–93.