PROVIDING ACCESS TO INFORMATION SYSTEMS OF HIGHER EDUCATION IN THE CASE OF LOSS OF KEY INFORMATION
Кипарисова А.И.1, Ажмухамедов И.М.2
1 Студентка, Астраханский государственный университет 2 Доктор технических наук, Астраханский государственный университет
ОБЕСПЕЧЕНИЕ ДОСТУПА К ИНФОРМАЦИОННЫМ СИСТЕМАМ ВЫСШЕГО УЧЕБНОГО ЗАВЕДЕНИЯ В СЛУЧАЕ УТРАТЫ КЛЮЧЕВОЙ ИНФОРМАЦИИ
Аннотация
Рассмотрены криптографические протоколы разделения секрета, проведен сравнительный анализ пороговых схем данного алгоритма и выбрана наиболее эффективная схема - схема Шамира для обеспечения доступности к данным в информационных системах ВУЗа в случае утраты ключевой информации.
Ключевые слова: протокол разделения секрета, пороговая схема Шамира, ключевая информация.
Kiparisova A.I.1, Azhmuhamedov I.M.2
1 Student, Astrakhan State University 2 PhD in Engineering, Astrakhan State University
PROVIDING ACCESS TO INFORMATION SYSTEMS OF HIGHER EDUCATION IN THE CASE OF LOSS OF KEY INFORMATION
Abstract
Cryptographic Protocols of secret sharing are reviewed, a comparative analysis of threshold circuits of this algorithm is carried out and the most effective scheme is chosen - the scheme of Shamir, to ensure the availability of data in information systems of the University in the event of loss of key information.
Keywords: secret sharing protocol, threshold scheme of Shamir, the key information
Modern higher education is characterized by a variety of information links both in the administration and in the areas of core business: the organization and conduct of the educational process, teaching and research activities, the financial administration, personnel management and accounting.
The information systems of higher education store large amounts of data, the protection of which involves the use of key information [4]. Key information ensures the confidentiality of data, but in the case of its loss the access to information systems may be lost.
To reduce the possibility of losing access to data in case of loss of key information in several ways:
- to use the backup key information and keep copies in different places;
- to entrust key information to several people;
- to use of cryptographic protocols secret sharing.
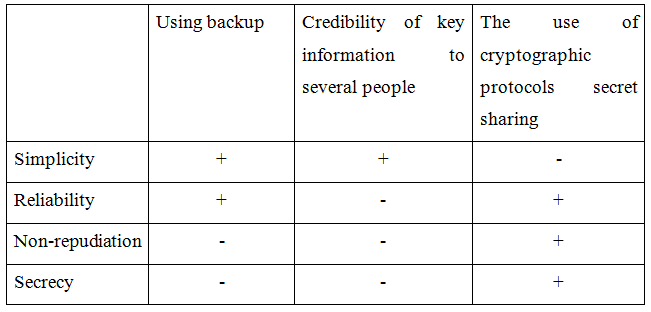
We compare these methods by criteria such as simplicity, reliability, non-repudiation and confidentiality (table 1).
Table 1 − Comparative analysis of the ways to reduce the contingency of loss of access
The table 1 shows that the most effective way to reduce the likelihood of loss of availability in case of loss of key information ̶ is the use of cryptographic secret sharing protocols.
In most cryptographic algorithms the protection, eventually, is based on a secret key. The main problem is in the organization of the secret key storage, because if an attacker manages to get that secret key, the protected information can with high probability to be in his hands. One of the existing methods of storing the secret key is a way to divide it between the people group, each of which will hold a part of the secret key. When it is needed, the private key can be reconstructed on the basis of parts. Part of the secret key itself does not carry any sensitive information [1].
Initially, reports of secret sharing created with the aim of eliminating the need for backup keys. Without a backup key is easy to lose the last one. Too large number of such copies also creates big problems - a low level of secrecy. A potential solution to this problem is the division of secret algorithms - they can be used to raise reliability without increasing the risk of disclosure of key information.
Secret sharing protocol consists of two main phases:
- Separation secret – phase distribution, the dealer who knows the secret of M, generates a fraction of с1, с2 ,..., сn with secret and will issue to each participant's share of a secure communication channel. Distributing is needed to be organized so that the expanded group of participants gathered together could definitely restore the object, and unresolved – they could not.
- The recovery phase of the secret when the structure of an access group (non-empty set of all access groups) brings its share with the secrets and get the secret.
There are a number of threshold secret sharing schemes:
- The scheme of Shamir;
- the scheme of Blakely;
- the schemes based on the Chinese remainder theorem.
The secret sharing scheme is perfect, if you share any secrets protected by the coalition does not contain any information about the aggregate secret.
The perfect secret sharing schemes ̶ this is when all the parts of the secret and the secret of the same size can be any value equal probability of allowable values in this scheme.
Compare the data schema for the perfect and ideal (table 2).
Table 2 − Comparative analysis of the secret sharing protocol schemes
The scheme of Shamir is the perfect and ideal one. The idea is based on this diagram is that, for the interpolation polynomial of degree (k-1) to the required point. If the minimal number of known points, interpolation is impossible.
The features of Shamir threshold scheme:
- - extensibility of the private key (for the newly emerged members of the protocol) can be calculated and distributed without the use of already existing parts, simply by calculating the additional points for the polynomial;
- - flexibility – the ability to assign different "weight" of different subsets of the authorization;
- - homomorphism property – for the scheme Shamir holds homomorphism.
- - effectiveness of a specific mechanism for arithmetic calculations – for example, multiplication by a constant: each participant protocol can multiply their private key part of the constant;
- - independence – unlike many cryptographic schemes, safety separation schemes secret key is not directly dependent on the complexity of the key [2].
Figure 1 is a block diagram which implements the secret sharing the scheme of Shamir, wherein:
- - p – is a large prime number (M is greater than any secret, which is supposed to share in the scheme);
- - n – is the number of shares of the secret;
- - k – is the minimum size allowed the group;
- - r1,…, rn – are unclassified non-zero elements (r<p);
- - s1,…,sk-1 – are arbitrary elements (s<p);
- - i=1,2,…,n;
- - S(x)= sk-1 xk-1 + sk-2 xk-2 + … + s1x + M mod p – generation of secret shares;
- - c1 = S (r1 ) mod p – share the secret;
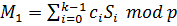 – the formula of the interpolation polynomial Lagrange, wherein
– the formula of the interpolation polynomial Lagrange, wherein 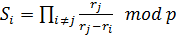 .
.
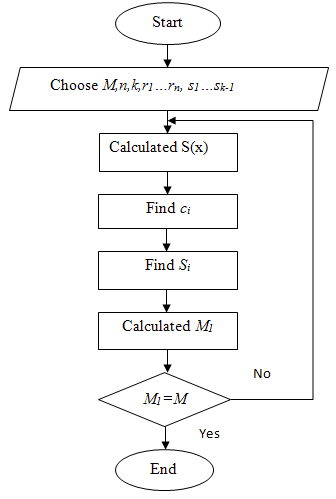
Figure 1 – The block diagram of the algorithm of Shamir
Thus, the use of a cryptographic Protocol of secret sharing scheme of Shamir, allows to increase the reliability of protection of data stored in information systems of higher educational institutions and makes it impossible to compute the secret illegitimate group of participants.
The scheme will be further implemented in the form of a software product in the programming language C#.
References
- Baranovskij K. Sovremennye sredstva hranenija kriptograficheskih kljuchej [Electronic resource] // Tehnologii bezopasnosti: jelektron. nauchn. zhurn. 2011. №3. URL http://aercom.by/wp-content/uploads/magazine/2011/3(18)/tb_3_2011_ok_45-50.pdf (Accessed: 15.01.2016);
- Gashenko A.V. Razdelenie sekreta (Secret Sharing) [Electronic resource] // Moskovskij fiziko-tehnicheskij institut. URL: http://re.mipt.ru/infsec/2004/essay/2004_Secret_Sharing__Gashchenko.htm (Accessed 15.01.2016);
- Shnajer B. Prikladnaja kriptografija. Protokoly, algoritmy, ishodnye teksty na jazyke Si Applied Cryptography. Protocols, Algorithms and Source Code in C. – M.: Triumf, 2002. S. 588 – 591. – 816 s.
- Azhmuhamedov I.M. Dinamicheskaja nechetkaja kognitivnaja model' ocenki urovnja bezopasnosti informacionnyh aktivov VUZa // Vestnik AGTU. Serija: «Upravlenie, vychislitel'naja tehnika i informatika». 2012. №2. S.137-142.