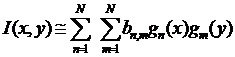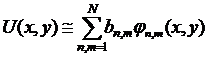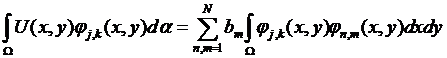RECONSTRUCTION OF TWO-DIMENSIONAL RADIO IMAGES OF THE SOURCES WITH SUPERRESOLUTION

Чикина А.Г.

Аспирант, Московский технологический университет (МИРЭА)

Работа выполнена при поддержке гранта РФФИ №14-07-00206а

ФОРМИРОВАНИЕ ДВУМЕРНЫХ РАДИОИЗОБРАЖЕНИЙ ИСТОЧНИКОВ СО СВЕРХРАЗРЕШЕНИЕМ

Аннотация

В статье теоретически обоснованы и проверены в ходе численных экспериментов на математической модели новые алгоритмы цифровой обработки двумерных сигналов, позволяющие повысить эффективную угловую разрешающую способность систем наблюдения на основе приближённого решения интегральных уравнений Фредгольма и довести её до сверхразрешения.

Ключевые слова: сверхразрешение, обратные задачи, регуляризация задачи, критерий Рэлея, интегральное уравнение Фредгольма

 

Chikina A.G.

Postgraduate student, Moscow Technological University

RECONSTRUCTION OF TWO-DIMENSIONAL RADIO IMAGES OF THE SOURCES WITH SUPERRESOLUTION

Abstract

New methods and algorithms of digital processing of the signals are theoretically proved and checked up during numerical experiments on mathematical model, allowing to increase effective angular resolution of measuring systems on the basis of the approached decision of integral equations.

Keywords: Superresolution, inverse problems, the regularization problem, the Rayleigh criterion, the Fredholm integral equation.

Цифровая обработка принимаемых сигналов по специальным алгоритмам позволяет получать дополнительную информацию об угловом распределении интенсивности источника сигналов, что эквивалентно увеличению эффективной угловой  разрешающей способности системы [1-7]. Представляемые методы обработки позволяют получить разрешение, превышающее критерий Рэлея, т.е. добиться сверхразрешения.

Алгебраические методы решения одномерных задач, предложенные в работах [3-5], заключаются в представлении приближённых решений в виде конечных разложений по задаваемым последовательностям функций с неизвестными коэффициентами. Данные методы оказываются перспективными и для двумерной задачи восстановления изображений источников сигналов, так как их обобщение на двумерные случаи [2] не приводит к серьёзному усложнению алгоритмов, а время численного решения при этом изменяется незначительно.

Пусть сектор обзора угломерной системы представляет собой телесный угол Ω₀. Используется узкая диаграмма направленности (ДН) f(x,y), где за нулевое принято направление на условный центр Ω₀, а x,y - это углы отклонения от нулевого направления в декартовой системе координат. Внутри сектора обзора расположен объект наблюдения с неизвестными в общем случае, конечными угло­выми размерами Ω.

Искомое двумерное угловое распределение излучаемого источником (или отражённого) сигнала обозначим I(x,y). Тогда на выходе приёмного устройства при сканировании сектора получим зависимость огибающей сигнала в виде U(x,y). Cвязь величин I, U и ДН выражается в виде линейного интегрального уравнения (ЛИУ) Фредгольма первого рода типа двумерной свёртки:

                    (1)

Задача состоит в восстановлении углового распределения I(x,y) на основе анализа принятого сигнала U(x,y) и известной ДН системы с максимально возможным угловым разрешением, превышающим критерий Рэллея.

Поставленная задача является некорректной, т.к. не удовлетворяет второму и третьему требованию корректности задачи по Адамару [1,5-7]. Для поиска приближённого решения, исходя из вида U(x,y), производится оценка положения и размеров телесного угла Ω, в котором расположен источник сигналов. Размеры и расположение Ω уточняются в ходе итерационного процесса. Искомое распределение I(x,y) можно представить в виде разложения по конечной системе ортогональных в Ω двумерных функций с неизвестными коэффициентами:

 .                                    (2)

Принятый сигнал представим в виде:

,  , (3)

где коэффициенты разложения b_n,m получим, из решения системы

,  j,k = 1,2…N    (4)

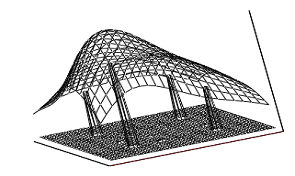
Количественные характеристики увеличения разрешения и его пределы исследовались на математической модели. Результаты восстановления изображения четырёх источников сигналов приведены на рис.1. По горизонтальным осям отложены углы x и y.

Рис.1. Восстановленное изображение

На рис.1 отображены исследуемый принимаемый сигнал U(x,y) – криволинейная поверхность, и четыре источника сигналов, найденные при обработке U(x,y) по алгоритму на основе (1-4). Полученное решение правильно отразило количество объектов, практически точно передало их расположение. Интенсивности были определены с небольшой ошибкой, составившей 2-5%.

Литература

1. Лаговский Б.А., Самохин А.Б. Алгебраические методы восстановления изображения источников радиоизлучения с повышенным угловым разрешением // Электромагнитные волны и электронные системы. – 2009. – Т.14, № 9. – С. 7-18.
2. Лаговский А.Б., Шумов И.Ю. Восстановление двумерных изображений источников излучения со сверхразрешением // Антенны. – 2013. – № 4. – С. 60-65.
3. Лаговский Б.А. Методы повышения эффективного углового разрешения малоразмерных целей в задачах радионавигации и  радиолокации.  // Антенны. – 2007. –  № 9 (124). –  C. 50 -55.
4. Лаговский Б.А. Восстановление изображения групповой цели цифровыми антенными решетками // Антенны. – 2011. – № 2(165). –  С. 40 -46.
5. Lagovsky B.A. Superresolution: Simultaneous orthogonalization of function systems describing the received signal and its source. // Progress in Electromagnetics Research Symposium Proceedings (Moscow, August 19–23, 2012). –  2012.  –  P. 993-996.
6. Lagovsky B.A. Image restoration of the objects with superresolution on the basis of spline – interpolation. // Progress in Electromagnetics Research Symposium Proceedings (August 19–23, 2012). – 2012. – P. 989-992.
7. Лаговский Б.А., Чикина А.Г. Решение обратных задач получения сверхразрешения на основе симметризации данных // Актуальные проблемы гуманитарных и естественных наук. – 2015. – № 4-1 – С. 20-23.

References

1. Lagovskij B.A., Samohin A.B. Algebraicheskie metody vosstanovlenija izobrazhenija istochnikov radioizluchenija s povyshennym uglovym razresheniem // Jelektromagnitnye volny i jelektronnye sistemy. – 2009. – T.14, № 9. – S. 7-18.
2. Lagovskij A.B., Shumov I.Ju. Vosstanovlenie dvumernyh izobrazhenij istochnikov izluchenija so sverhrazresheniem // Antenny. – 2013. – № 4. – S. 60-65.
3. Lagovskij B.A. Metody povyshenija jeffektivnogo uglovogo razreshenija malorazmernyh celej v zadachah radionavigacii i  radiolokacii.  // Antenny. – 2007. –  № 9 (124). –  C. 50 -55.
4. Lagovskij B.A. Vosstanovlenie izobrazhenija gruppovoj celi cifrovymi antennymi reshetkami // Antenny. – 2011. – № 2(165). –  S. 40 -46.
5. Lagovsky B.A. Superresolution: Simultaneous orthogonalization of function systems describing the received signal and its source. // Progress in Electromagnetics Research Symposium Proceedings (Moscow, August 19–23, 2012). – 2012.  –  P. 993-996.
6. Lagovsky B.A. Image restoration of the objects with superresolution on the basis of spline – interpolation. // Progress in Electromagnetics Research Symposium Proceedings (August 19–23, 2012). – 2012. – P. 989-992.
7. Lagovskij B.A., Chikina A.G. Reshenie obratnyh zadach poluchenija sverhrazreshenija na osnove simmetrizacii dannyh // Aktual'nye problemy gumanitarnyh i estestvennyh nauk. – 2015. – № 4-1 – S. 20-23.