On the 36th Order Discrete Group for a Multiplicative Class of 2nd Order Differential Equations

Дискретные группы преобразований для обыкновенных дифференциальных уравнений были открыты В. Ф. Зайцевым

Благодаря дискретно-групповому анализу обыкновенных дифференциальных уравнений, В. Ф. Зайцеву и его научной школе удалось найти точные решения сотен ОДУ, которые включены в справочники конца 20-го – начала 21-го веков, например

В данной работе исследуется класс ОДУ 2-го порядка с мультипликативными правыми частями:

(1)

а также его подкласс при :

(2)

Обозначим их соответственно .

Несколько странный 4-й сомножитель в правой части (1) имело смысл включить в (1) для получения замкнутости некоторых дискретных преобразований в классе уравнений (1), которые не являются замкнутыми в (2).

2.1. Основные определения

Определение 1. Множество преобразований G, замкнутых на выбранном классе уравнений D, называется дискретной группой преобразований G, допускаемой классом уравнений D

Определение 2. Множество элементов данной дискретной группы G называется множеством порождающих (образующих) элементов, если всякий элемент группы G можно выразить в виде конечного произведения их степеней (в том числе с отрицательными показателями)

Определение 3. Соотношения между образующими элементами дискретной группы G называется её определяющими соотношениями, если всякое другое соотношение между образующими является их алгебраическим следствием

Определение 4. Кодом дискретной группы G называется совокупность образующих и определяющих соотношений

Замечание 1. Иногда кодом дискретной группы называют только совокупность определяющих соотношений между образующими.

Определение 5. Группой диэдра Dq порядка 2q называется дискретная группа с двумя образующими u и v, связанных следующими определяющими соотношениями:, где E – тождественное преобразование

2.2. Дискретная группа преобразований 6-го порядка для класса уравнений (2)

Класс уравнений (2) включает в себя в качестве подкласса класс обобщённых уравнений Эмдена-Фаулера (ОУЭФ), когда K, L, M являются степенными функциями:

(3)

Обозначим его (k, l, m|A) или (k, l, m).

Класс уравнений (3) был подробно исследован В. Ф. Зайцевым и он имеет достаточно много приложений при определённых значениях показателей: модель политропного газового шара (модель звезды), уравнение Томаса-Ферми движения электронов и т.д.

Были найдены дискретные преобразования

(4)

а также преобразование Беклунда, зависящее от параметров исходного уравнения

(5)

Преобразования r и g являются образующими группы преобразований диэдра 6-го порядка:

(6)

(E – тождественное преобразование).

Оказалось, что аналогичные преобразования действуют и в классе уравнений (2), в частности, то же точечное преобразование

(7)

а также обобщение преобразования Беклунда (5) (назовём его той же буквой)

(8)

(показатель «-1» в (8) означает обратную функцию).

Граф группы преобразований диэдра D3 (6) 6-го порядка для класса уравнений (2) изображён на рис. 1.

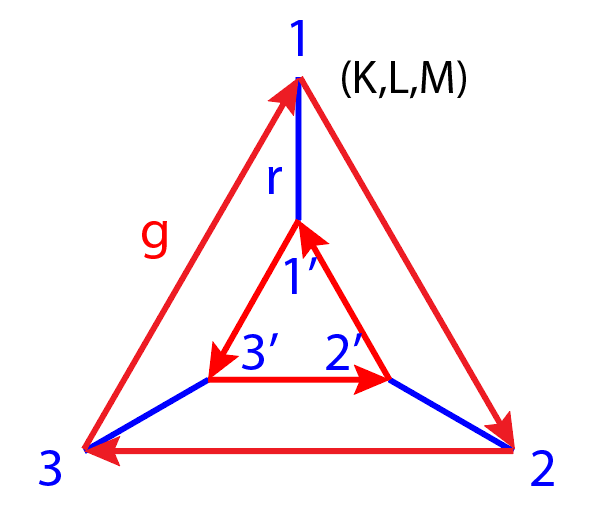
Рисунок 1 - Граф группы D3

DOI:10.23670/IRJ.2024.140.39.1

На рис. 1 вершины графа соответствуют уравнениям класса (2), а дуги графа обозначают преобразования группы D3 (6).

2.3. Дискретная группа преобразований 12-го порядка для класса уравнений (1)

Для класса уравнений (1) была найдена

(9)

образующими которой являются точечное преобразование

(10)

и касательное преобразование

(11)

Граф группы D6 изображён на рис. 2.

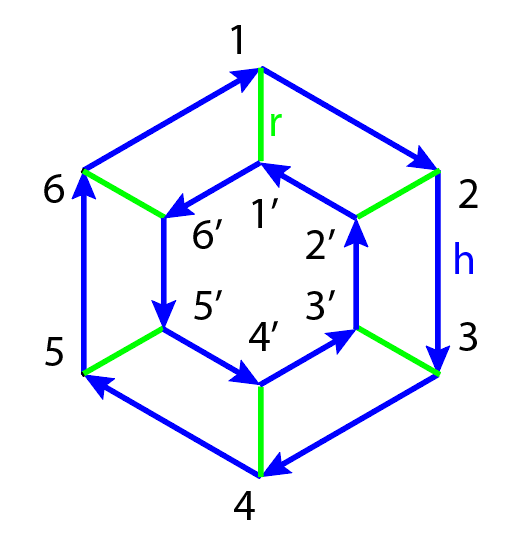
Рисунок 2 - Граф группы D6

DOI:10.23670/IRJ.2024.140.39.2

2.4.      Дискретная группа преобразований 36-го порядка для класса уравнений (2)

Поскольку (2) является подклассом класса уравнений (1), то к вершинам графа группы D3 на рис. 1 можно присоединить графы групп D6. Таким образом, получается граф 36-го порядка, изображённый на рис. 3 (преобразование r опущено, поэтому показанные на рис. 3 18 вершин на самом деле удваиваются).

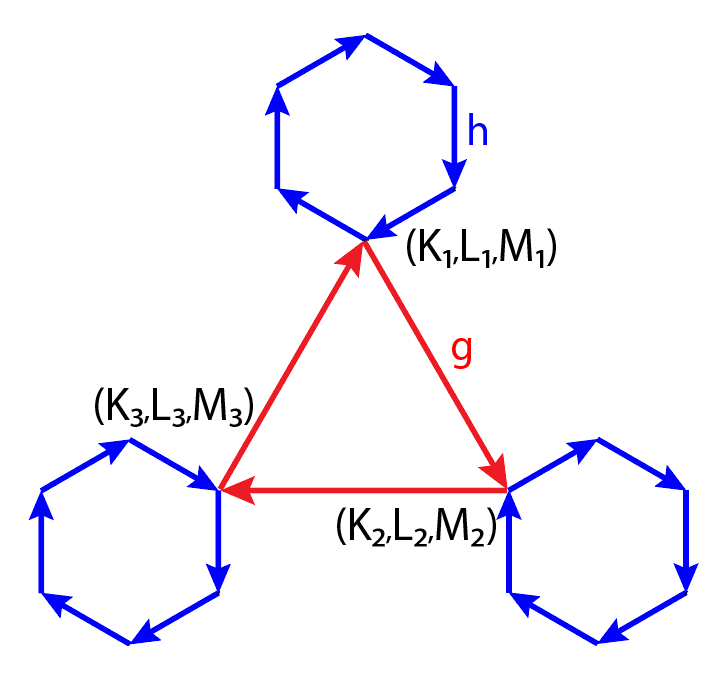
Рисунок 3 - Граф группы 36-го порядка

Примечание: преобразование r и дополнительные 18 вершин опущены

DOI:10.23670/IRJ.2024.140.39.3

2.5. Получение точных решений уравнений

Рассмотрим уравнение свободных колебаний маятника

(12)

дискретные симметрии которого были частично исследованы в работе [9].

Поскольку уравнение (12) принадлежит классу уравнений (1), то к нему можно применить группу преобразований D6 (9).

Так как уравнения 2-6’ в таблице 1 связаны с уравнением 1 известными преобразованиями – преобразованиями группы D6 (9), то общие решения этих 11 уравнений также можно вычислить, поскольку решения уравнений связаны теми же самыми преобразованиями, что и сами уравнения.

Пример 1.

Легко проверить, что уравнение (12) под номером 1 в таблице 1 имеет следующее частное решение в параметрическом виде:

(13)

где  – параметр.

Найдём, к примеру, решение уравнения 2’.

По графу на рис. 2 легко видеть, что уравнение 2’

(14)

приводится к уравнению 1 с помощью преобразования hr:  

где hr – известное преобразование Лежандра:

(15)

Следовательно, решения уравнений 1 и 2’ связаны этим же преобразованием. Таким образом, решение уравнения 2’ (14) является композицией преобразования (15) и решения (13) уравнения колебаний маятника 1:

(16)

2.6. Пример построения дискретной группы 36-го порядка. Метод расширения

Уравнение (12) принадлежит обоим классам уравнений – (1) и (2), для которых построены дискретные группы диэдра – D6 и D3 соответственно.

Группа D6 применена к уравнению (12) в пункте 5. А вот группа D3 не может быть полностью применена к уравнению (12) в силу теоремы, приведенной в [1]: класс уравнений (2) допускает группу D3 при . А для уравнения (12) .

Чтобы снять это ограничение, применим метод расширения: поместим уравнение (12) в следующий класс уравнений:

(16)

который обозначим

(17)

Коэффициент A в (17) опустим, так как он несущественен: его можно изменять с помощью преобразования масштабирования.

Класс уравнений (16), в отличие от уравнения (12), допускает группу преобразований D3. Уравнения, соответствующие вершинам графа на рис. 1, помещены в таблицу 2.

Таблица 2 - Уравнения-вершины графа на рис. 1

DOI:10.23670/IRJ.2024.140.39.5

Преобразование  зависит от функций K, L, M исходного уравнения (в соответствии с (8)), поэтому оно имеет различный вид, будучи применённым к разным уравнениям-вершинам:

Так как класс уравнений (16) принадлежит классу уравнений (1), то он допускает группу D6, которую можно применить к вершинам 1, 2, 3 графа на рис. 2. В результате, уравнение (16) допускает дискретную группу преобразований 36-го порядка, граф которой изображён на рис. 3.

2.7. Пример получения точного решения с помощью группы 36-го порядка

Рассмотрим уравнение

(18)

в качестве исходного. Пусть оно соответствует вершине 1.1 на рис. 4

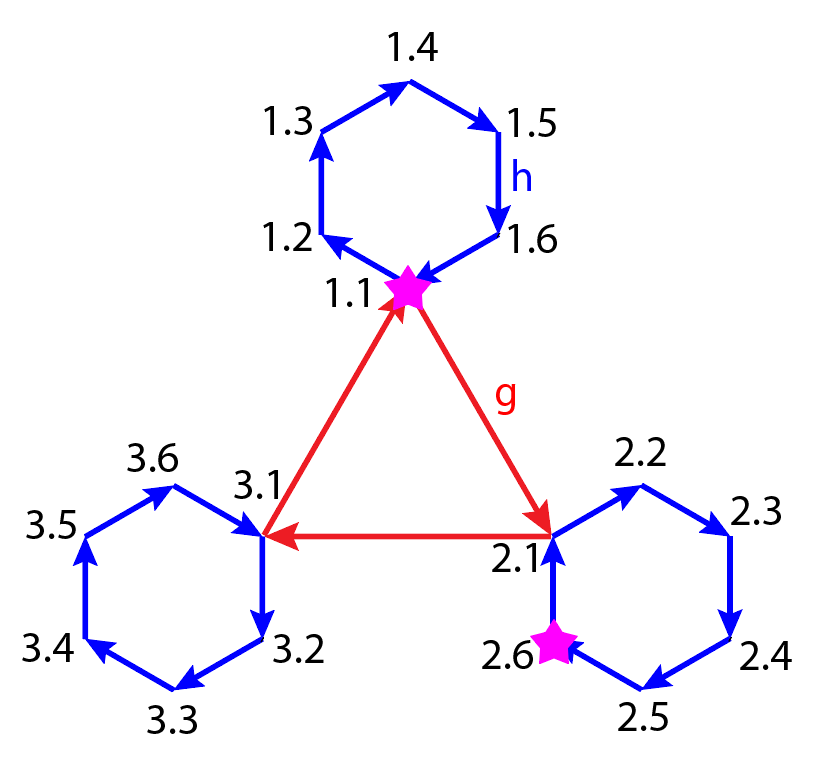
Рисунок 4 - Граф группы 36-го порядка для примера 2

Примечание: преобразование r и дополнительные 18 вершин опущены

DOI:10.23670/IRJ.2024.140.39.6

Согласно

[6]

, общее решение уравнения (18):

(19)

где  – коэффициенты, зависящие от A и C1 (C1, C2 – произвольные постоянные).

Найдем, к примеру, общее решение уравнения

(20)

соответствующее вершине 2.6 графа на рис. 4.

Легко видеть, что , поэтому общее решение уравнения 2.6 (20) есть композиция преобразования hg2 и общего решения уравнения 1.1 (19):

(21)

где , где a2 и b2 – коэффициенты, зависящие от B и C1; P4 указано выше.

В данной работе продолжено исследование мультипликативных классов уравнений (1), (2), (3), начатое в работах

В работе

Для класса уравнений (1) построена дискретная группа преобразований 12-го порядка, а для класса уравнений (2) – 36-го порядка.

Изложен метод «размножения» – получения новых разрешимых случаев в исследуемых классах уравнений. Приведены примеры нахождения точных решений уравнений редукцией к уравнению колебаний маятника (по группе 12-го порядка), а также с помощью общего решения одного из обобщенных уравнений Эмдена-Фаулера (по группе 36-го порядка).

В дальнейшем можно попытаться применить рассмотренную технику для класса уравнений с несколькими мультипликативными слагаемыми.