A Calculation Model of Ferromagnetic Lubricant in a Sliding Knife Edge with a Non-standard Surface
A Calculation Model of Ferromagnetic Lubricant in a Sliding Knife Edge with a Non-standard Surface
Abstract
The work presents a methodology for the formation of a calculation model of a thrust sliding bearing with a non-standard bearing area and a fusible rim surfacing. The case is examined when a compressible ferromagnetic fluid and a coating melt having similar rheological properties are used as a hydrodynamic lubrication model in the presence of an electromagnetic field. As a result, analytical expressions for bearing capacity and for friction force have been obtained. The influence of parameters characterizing the adapted friction (nonlinear) and elastically deformed contour of bearing support area as well as the parameter conditioned by the presence of melt on the main operational characteristics of the bearing are evaluated.
1. Введение
Без использования надежной и высокопроизводительной техники в машиностроении, авиастроении, приборостроении и т.д., которое можно достичь за счет создания механизмов на стадии проектирования для принятия принципиальных решений о конструктивном исполнении деталей и их сопряжений, применяемых материалов, невозможно обеспечить необходимый уровень надежности.
Повышение ресурса подшипников скольжения является важной задачей, имеющей большое экономическое значение. В связи с этим вызывает интерес использование в качестве модели гидродинамического смазывания жидкий смазочный материал и расплав покрытия контактных поверхностей.
Работы
, , , посвященные гидродинамическому расчету трибосистем с учетом реологических свойств, применяемых смазочных материалов, обладающих Ньютоновскими или Неньютоновскими свойствами при ламинарном и турбулентном режиме течения для увеличения гидродинамического режима смазывания для различных условий эксплуатации, доказывает необходимость учета дополнительных факторов.Анализируя работы
, , , трибоситем с покрытиями из различных антифрикционных композитов, с учетом стратификации жидкого смазочного материала, а также исследований , , , трибосистем с нестандартным профилем на рабочей поверхности выявлено, что учет вышеперечисленных факторов улучшает вибропоглощающие свойства подшипников скольжения и снижает их температуру. Установлено, что при учете варьирования вида конструкции подшипника и антифрикционного покрытия можно разработать эффективные конструкции для применения в трибоузлах машин и механизмов.Для уменьшения износа в работах
, , , проведено исследование трибосистем с легкоплавким металлическим покрытием с учетом реологических свойств применяемого смазочного материала и расплава покрытия, при ламинарном и турбулентном режимах течения смазочного материала, позволяющее эффективно управлять показателями надежности и долговечности трибоузлов для различных условий эксплуатации.Настоящее исследование посвящено расширению области применения путем разработки математических моделей клиновидной опоры скольжения, учитывающей дополнительные факторы: сжимаемость, антифрикционное покрытие, электропроводность, упругая опорная поверхность ползуна, адаптированный к условиям трения опорный профиль ползуна, а также расплав покрытия для различных условий эксплуатации.
2. Постановка задачи
Рассматривается установившееся течение сжимаемой ферромагнитной жидкости в зазоре клиновидной опоры скольжения, ползун с нестандартным профилем неподвижен, а опорное кольцо с покрытием движется в сторону сужения зазора со скоростью u* (см. рисунок). Помимо этого, предполагается, что адаптированный контур ползуна является также нелинейным.
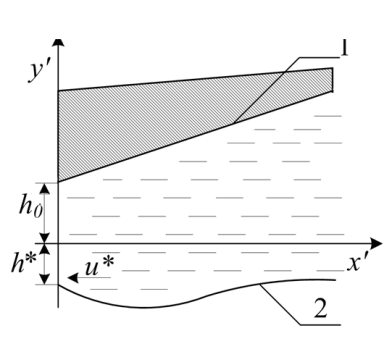
Рисунок 1 - Расчетная схема:
1 - контур ползуна; 2 - расплавленный контур покрытия направляющей
1) контур ползуна, прилегающий к жесткой опорной поверхности;
2) деформированный контур ползуна;
3) недеформированный контур ползуна;
4) направляющей до расплава;
5) контур направляющей после расплава. Уравнения этих контуров запишем в виде:
Где функция подлежит определению.
Будем исходить из следующих базовых уравнений: уравнения движения сжимаемой ферромагнитной жидкости, уравнения неразрывности, уравнения состояния, уравнения Ламэ, а также уравнения, описывающего расплавленный контур направляющей. К этим уравнениям необходимо также добавить уравнение Максвелла. Указанная система уравнений в системе координат x'Oy' запишется в виде:
Предполагается, что скорость движения опорного кольца достаточно большая, а поверхность рассматриваемого ползуна – шероховатая. Такая система соответствует квадратичной области движения смазочного материала, в которой потери давления на трение пропорциональны квадрату скорости скольжения
где L – длина ползуна; u* – скорость скольжения направляющей; λ – коэффициент потерь на трение, находится по формуле Шифринсона λ = 0,11 δ*/h0, δ* = 0,005 мм – высота шероховатости ползуна.
Для удобства решения переходим к безразмерным величинам:
а) в смазочном слое:
в) в упругом слое
где – характеризует величину компонента вектора перемещения.
Подставляя (4) и (5) в (2), будем иметь:
Здесь
В начале решаем задачу для экстремального случая, когда . В этом случае
. В дальнейшем в первом уравнении системы (6) заменим значение скорости ее максимальным значением (v = –1).
Систему уравнений (6) решаем при общепринятых граничных условиях:
где
α* – постоянная Мусхелишвили;
Далее решаем задачу (6)–(7) для случая, когда . В этом предельном случае имеем:
С учетом (8) точное автомодельное решение задачи (6)–(7) будем искать в виде:
Подставляем (9) в (6) и (7), будем иметь:
Для нахождения давления р получаем аналитическое выражение:
Используя метод последовательных приближений для (11) имеем:
Используя (10) и (12), для несущей способности и силы трения получим выражения вида
В заключение отметим, что при промежуточных значениях удельной теплоты плавления (т. е. ) формула (13) остается в силе и в рассматриваемом случае, если
заменим на
.
Численный анализ по результатам теоретического исследования проведен для значений r = 20 мм; V = 1–3 м/с; σ = 4,1–28,5 МПа; μ0 = 0,0707–0,0076 Н·с/м2.
Триботехнические экспериментальные исследования упорных подшипников были проведены на специальном стенде для триботехнических исследований (модель НС12).
Конструкция образцов для экспериментальных исследований упорных подшипников скольжения состоит из плоской опоры и сопрягаемого с ней контртела. Опора имеет покрытие рабочей поверхности из металлического сплава Вуда.
Таблица 1 - Сравнительный анализ результатов исследования ползуна с металлическим покрытием клиновидной опоры скольжения с нестандартной поверхностью
№ | Теоретическое исследование | Экспериментальное исследование | ||||
Метал. покрытие | Покрытие и упругая опорная поверх-ть | Упругоадаптиро-ванная опорная пов-ть с покрытием | Метал. покрытие | Покрытие и податл. опорная поверх-ть | Упругоадаптиро-ванная опорная пов-ть с покрытием | |
1 | 0,021 | 0,0227 | 0,02 | 0,0174 | 0,0149 | 0,0133 |
2 | 0,0193 | 0,0168 | 0,0158 | 0,0109 | 0,0077 | 0,0061 |
3 | 0,00165 | 0,00146 | 0,00136 | 0,0086 | 0,0068 | 0,0054 |
4 | 0,00180 | 0,00156 | 0,00142 | 0,0112 | 0,0087 | 0,0069 |
5 | 0,0022 | 0,00189 | 0,00161 | 0,0142 | 0,0113 | 0,0099 |
3. Заключение
1. Получена новая математическая модель, позволяющая установить основные закономерности процессов трения и изнашивания клиновидной опоры скольжения с металлическим покрытием поверхности опорного кольца и не линейным адаптированным контуром ползуна при учете сжимаемости смазочного материала и электропроводности ферромагнитного смазочного материала.
2. В результате численного анализа установлено, что применение таких подшипников с учетом вышеперечисленных факторов (сжимаемость, электропроводность, реологические свойства смазного материала и расплава покрытия) повышает несущую способность (на 11–12 %), а коэффициент трения снижается на 9–11 %.
3. Триботехнические испытания на торцевой машине трения показали значительное (до 24 %) уменьшение пятна износа и более длительное (до 32 %) сохранение гидродинамического режима в присутствии покрытия на поверхности направляющей и упруго-адаптированного профиля ползуна по сравнению с исходным смазочным материалом.
Условные обозначения:
L' – удельная теплота плавления на единицу объема; v'x', v'y' – компоненты вектора скорости; p' – гидродинамическое давление; ρ' – плотность; σ' – электропроводность; – вектор магнитной индукции;
– вектор напряженности электрического поля; Δ – оператор Лапласа;
– компоненты вектора переменных;
– постоянная Ламэ; G – модуль сдвига.
