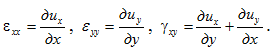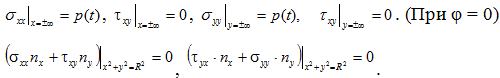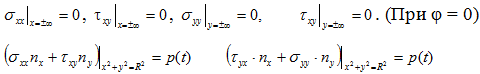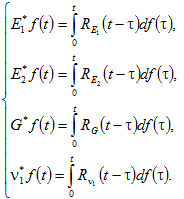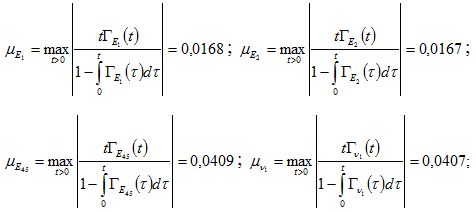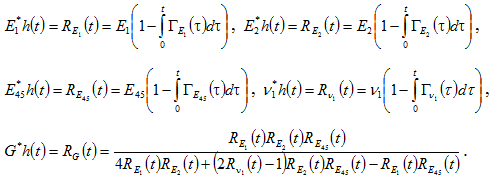О РЕШЕНИИ НЕКОТОРЫХ КРАЕВЫХ ЗАДАЧ АНИЗОТРОПНОЙ ВЯЗКОУПРУГОСТИ

Шиверский А.В.¹, Горохов А.Ю.²

¹бакалавр, ²старший преподаватель, Пермский национальный исследовательский политехнический университет

О РЕШЕНИИ НЕКОТОРЫХ КРАЕВЫХ ЗАДАЧ АНИЗОТРОПНОЙ ВЯЗКОУПРУГОСТИ

Аннотация

Произведено численное решение задач о большой ортотропной линейно-вязкоупругой пластике с отверстием при различных видах нагружения. Задачи поставлены в многооператорной форме. Решение производилось приближённым методом квазиконстантных операторов. Установлено наличие заметной эволюции напряжений у кромки отверстия даже при постоянной внешней нагрузке. Произведена оценка роста коэффициента концентрации напряжений со временем.

Ключевые слова: анизотропия, многооператорная задача, линейная вязкоупругость, метод конечных элементов.

 Shiversky A.V.¹, Gorohov A. Yu.²

¹student; ²PhD in Technical Science, associate professor, Perm National Research Polytechnic University

ABOUT THE SOLUTION OF SOME BOUNDARY PROBLEMS OF ANISOTROPIC OF VISCOELASTICITY

Abstract

There was produced the numerical solution of the problem of large linear-viscoelastic orthotropic plate with a hole with different types of loading. Tasks are set in a multi-statement form. The decision was made by the approximate method of quasiconstant operators. There was established existence of the appreciable evolution of the stresses at the edge of the hole, even at a constant external load. There was produced assessment of growth of coefficient of concentration of tension over time.

Keywords: anisotropy, the task multi-statement, linear viscoelastic, finite element method.

Исследуются большие линейно-вязкоупругие ортотропные пластинки с отверстием при различных условиях нагружения. Рассматриваются следующие варианты нагружения: 1) всесторонние постоянные распределённые растягивающие усилия; 2) постоянное внутренне давление по кромке отверстия. В качестве материала будет рассмотрен стеклопластик КАСТ-В, параметры: E₁=2,6·10¹⁰ Па, E₂=1,52·10¹⁰ Па, ν₁=0,2, G=0,45·10¹⁰ Па. Считалось, что материал обладает несколькими независимыми вязкоупругими характеристиками. Для решения многооператорных задачи использован приближённый метод квазиконстантных операторов. Решение упругой задачи в каждый момент времени производилось методом конечных элементов с помощью пакета ANSYS. Исследована сходимость численного решения.

В силу симметрии поставленных задач будем рассматривать только четверть пластинки. При решении использованы четырёхузловые конечные элементы с линейной аппроксимацией. Вблизи концентратора сетка сгущалась.

Постановка задачи в рамках теории упругости:

Уравнения равновесия:

Геометрические соотношения:

Физические соотношения для ПНС пластинки:

               (1)

Граничные условия будут иметь следующий вид:

• Случай всестороннего растяжения пластины

• Случай давления по контуру кромки

φ – Угол между осями упругости и осями XY

Рассматриваемые упругие задачи имеют аналитические выражения для окружного напряжения σ_θ, приведённые в работе [1].

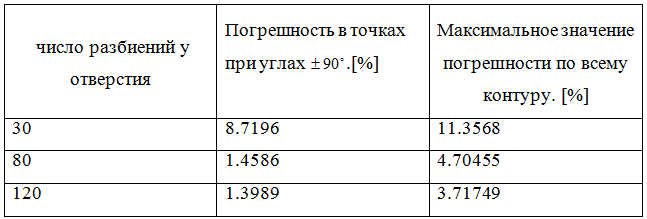
В ходе решения при уменьшении сетки приближённое решение стягивается к точкам с максимальными напряжениями, в данном случае это точки при углах ±90º. Вычислим погрешность в этих точках. Под погрешностью понимается модуль отношения разницы значений точного и численного решений к значению точного решения.

Таблица 1 - Демонстрация сходимости (для случая всестороннего растяжения)

 

Для решения поставленной задачи воспользуемся методом квазиконстантных операторов. Решение вязкоупругой задачи получим из решения упругой путем замены упругих постоянных вязкоупругими операторами. Упругие характеристики материала E₁, E₂, G, ν₁ заменяются на интегральные операторы. В этом случае физические соотношения (1) примут вид:

где , а   – интегральные операторы:

                                                            (2)

Зададим функцию скорости сдвиговой релаксации в виде функции А.Р. Ржаницина  .

(3)

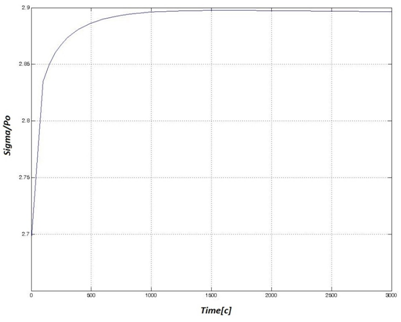
Экспериментальные значения параметров функций скоростей релаксации для материала КАСТ-В определяются из работы [2]: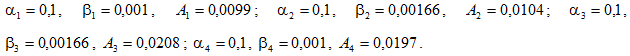

Определить показатели квазиконстантности операторов:

Показатели квазиконстантности операторов много меньше единицы, поэтому эти операторы можно считать квазиконстантными.

Следуя методу квазиконстантных операторов, мы имеем право, с некоторой погрешностью, считать решением вязкоупругой задачи в данный момент времени решение упругой задачи, в которой упругие параметры материала определяются значениями соответствующих вязкоупругих операторов, действующих на функцию внешней нагрузки:

При нагрузке в виде функции Хевисайда p=(h)t, получаем:

 (4)

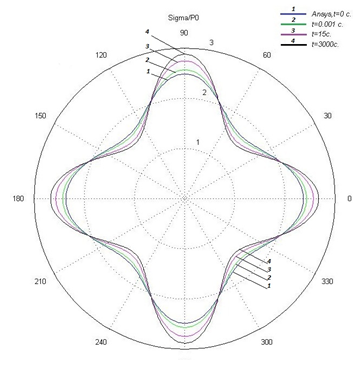
 Приведём эпюры перераспределения во времени окружных приведённых напряжений  возле кромки круглого отверстия,  для внутреннего давление по кромке отверстия, рис. 1.

 

 Рис. 1. Эволюция напряжений у кромки круглого отверстия, при внутреннем давление по кромке отверстия

 

Рис. 2. Изменение коэффициента концентрации напряжений во времени возле кромки круглого отверстия при внутреннем давление по кромке при угле

На рис 2 представлен график изменения во времени коэффициента концентрации напряжений у кромки круглого отверстия

У пластинки с отверстием, за рассмотренный период времени, концентрация напряжений увеличилась на 7,5%.То есть можно говорить о росте во времени концентрации напряжений в данном вязкоупругом стеклопластике при воздействии на него постоянной внешней нагрузки.

Рассмотрено решение краевых задач  теории упругости для анизотропного материала. Так же были получены эпюры приведённых окружных напряжений для двух видов нагружения и для различных случаев отверстия.

Решение поставленных задач линейной вязкоупругости наглядно подтверждает предположение об эволюции напряжённого состояния системы даже при постоянном внешнем нагружении. Были установлены закономерности изменения коэффициентов концентрации во времени, а также дана их количественная оценка.

Литература

1. Лехницкий С.Г. Теория упругости анизотропного тела. М.: Наука, 1977.
2. Огибалов П.М. Колтунов М.А. Тюнеева И.М. Экспериментально-теоретические методы определения упруго-вязких характеристик стеклопластиков // Упругость и неупругость. М.: Изд-во МГУ, 1971. – Вып. 2. С. 175-192.
3. Адамов А.А., Матвеенко В.П., Труфанов Н.А., Шардаков И.Н. Методы прикладной вязкоупругости. Екатеринбург: УрО РАН, 2003.

References

1. Lexnickij S.G. Teoriya uprugosti anizotropnogo tela. M.: Nauka, 1977.
2. Ogibalov P.M. Koltunov M.A. Tyuneeva I.M. Eksperimentalno-teoreticheskie metody opredeleniya uprugo-vyazkix xarakteristik stekloplastikov // Uprugost i neuprugost. M.: Izd-vo MGU, 1971. – Vyp. 2. s. 175-192.
3. Adamov A.A., Matveenko V.P., Trufanov N.A., Shardakov I.N. Metody prikladnoj vyazkouprugosti. Ekaterinburg: Uro Ran, 2003.