Substantiation of ozonator parameters for hive ozonization
Substantiation of ozonator parameters for hive ozonization
Abstract
The majority of bee families are in private subsidiary farms. It is necessary to help beekeepers in their fight against the main diseases of bee populations. The use of chemical drugs leads to the adaptation of pathogens and accumulation of dangerous substances in beekeeping products. Science and practice continue to search for new environmentally friendly ways to treat bee families. A lot of such research is carried out in Kuban SAU. For example, the use of ozonators makes it possible to prevent diseases and stimulate the development of bee families. It is necessary to continue research on increasing the efficiency of ozone use in beekeeping. For this objective, it is necessary to carry out modelling of the main physical processes occurring in the ozonator. A mathematical model of the main processes in the ozonator was developed and as a result of modelling in Comsol Multiphysics software rational parameters and modes of operation were established. It has also been found out that in case of connection of several hives to the output spigots, non-uniformity of ozone output concentrations is observed – practically twice. Additional installation of some structure is recommended to ensure the required uniformity of ozone supply to the hives.
1. Введение
Сегодня пчеловодство в России переносит сложные времена, и количество пчелиных семей продолжает сокращаться. На Кубани в 2023 году проходил круглый стол «Правоприменение и развитие законодательного регулирования пчеловодства в Российской Федерации» где отмечалось, что количество пчелосемей в России за последние десятилетия снизилось в три раза
. Сегодня известно, что большая часть пчелиных ульев находится в личных подсобных хозяйствах. Сокращение пчел влияет на производство меда и других продуктов пчеловодства. Также нужно отметить, что определяющая роль пчеловодства заключается не в получении меда, а в опылении отдельных сельскохозяйственных культур.Для успешного и продуктивного ведения пчеловодства необходимо постоянно следить за здоровьем пчелиных семей. На сегодня наиболее распространёнными болезнями пчел являются аскосфероз, нозематоз, варроатоз, и др. Пчеловоды опасаются распространения новой разновидности варротооза – клеща Тропи, с которым еще не найдены радикальные способы борьбы.
Сейчас большинство болезней пчел, пчеловоды лечат определенными антибиотиками. Постоянное применение антибиотиков в дальнейшем приведет к снижению их способности воздействовать на пораженные семьи, что связано с привыканием к ним болезнетворных организмов. Конечно, это вынуждает пчеловодов в первую очередь увеличивать дозу данных лекарств, что может уже негативно действовать и на самого пчеловода. Также в пчеловодстве замечено, что антибиотики попадают в продукты пчеловодства, что снижает их потребительские качества . В связи с этим ученые и пчеловоды продолжают поиск экологически чистых способов лечения пчелиных семей. К таким экологичным способам относится озонирование. Озон представляет собой сильный дезинфектант и способен разрушать болезнетворные микроорганизмы путем их окисления
, . Значительный вклад в разработку и внедрение озонаторов в пчеловодстве внесли ученые Кубанского ГАУ . Так, ими установлены следующие параметры для профилактики и лечения аскосфероза: концентрация озона 250 мг/м3, экспозиция 1 час; при значительном поражении семьи – концентрация газа увеличивается 2 раза – 500 мг/м3 с экспозицией 1 час. Овсянниковым Д.А. и его учениками установлены параметры и режимы работы озонирующих установок для профилактики и лечения нозематоза, варроатоза, и даже для уничтожения восковой моли. Эти ученые предложили обеззараживать соторамки, пораженные нозематозм озоном с концентрацией 100-400 мг/м3 в течение 12 часов . С самой проблемной болезнью – варроатозом можно бороться озонированием если подавать в улей его концентрацию 500-2000 мг/м3 с продолжительностью работы от 20 до 120 мин .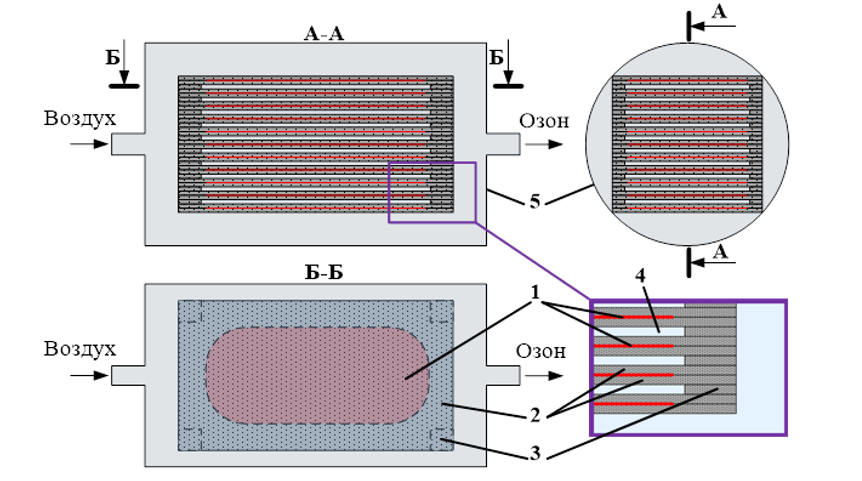
Рисунок 1 - Вид озонатора пластинчатого типа:
1 – проводящие электроды; 2 – диэлектрические барьеры; 3 – непроводящие вставки; 4 – разрядный зазор; 5 – корпус
2. Методы и принципы исследования
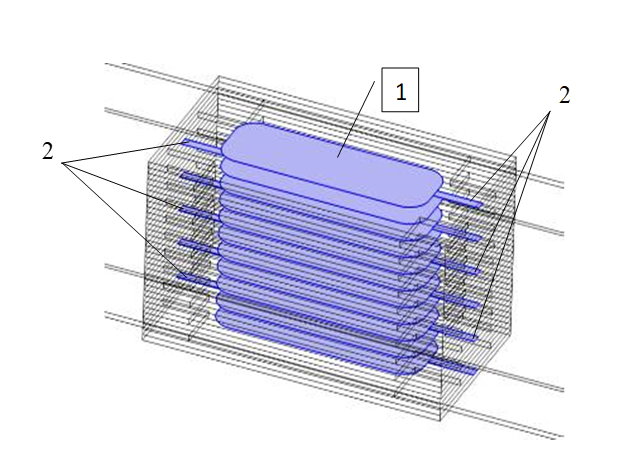
Рисунок 2 - Изображение разрядного устройства:
1 – электроды; 2 – контакты для подключения электродов к источнику питания
В результате взаимодействия образованных атомов кислорода и азота с их молекулами образуется озон:
Массовые доли отдельных химических составляющих в соответствии с выражением могут быть найдены следующим образом:
где:
ρ – плотность смеси, кг/м3;
ci – массовая доля i-го вещества, о.е.;
v – скорость смеси, м/с;
Ri – скорость химической реакции для i-го вещества, кг/(м3·с).
Транспортные свойства электронов можно установить на основании функции распределения энергий электронов (ФРЭЭ), которая задаётся одним из способов: по Максвеллу, Друйвестейну, уравнению Больцмана. Установлено
, что наилучшую сходимость при моделировании численными методами имеет ФРЭЭ по Максвеллу:где:
β1=Г(5/2g)3/2Г(3/2g)-5/2 и β2=Г(5/2g)Г(3/2g)-1;
ε – энергия электрона, эВ;
ϕ – средняя энергия электрона, эВ;
g – коэффициент равный единице;
Г – неполная гамма-функция.
Описать распределения электронов в разрядном промежутке возможно с помощью уравнения Больцмана, которое допускает движения электронов под действием внешних сил, в качестве которых выступают электрическое поле и воздушные потоки :
где:
ne – плотность электронов, 1/м3;
Ге – поток электронов, 1/(м2·с).
Поток электронов Ге под действием электрического поля можно описать следующим выражением:
где:
μе – подвижность электронов, м2/(В·с);
Е – напряженность электрического поля, В/м;
U – напряжение на электродах, В;
De – диффузия электронов, м2/с.
Параметр подвижности электронов μ_е определяется в соответствии с выражением: μе=μe⋅Nn/Nn, где Nn – число Лошмидта, 1/м3
:где:
p – давление, Па;
kB – постоянная Больцмана, 1,38·10-23, Дж/К;
T – температура, К.
Напряженность электрического поля описывается следующим уравнением:
где:
ε0 – электрическая постоянная, 8,8542·10-12 Ф/м;
εd – относительная диэлектрическая проницаемость среды, о.е.;
ρV – объемная плотность заряда, Кл/м3, (ρV=-(ne/NA)⋅F, где NA – число Авагадро, 1/моль; F – постоянная Фарадея, Кл/моль).
Принимаем, что движение воздушной смеси в установке будет турбулентным и расчеты будут проводиться с помощью модели Algebraic yPlus (данная модель чаще всего используется для описания процессов охлаждения электрооборудования), которая основана на уравнениях Навье-Стокса и для данной среды может быть представлена как:
где:
μ – коэффициент динамической вязкости воздуха, Па·с;
p – давление воздуха, Па;
I – единичный вектор;
g – ускорение свободного падения;
μT – турбулентная вязкость, Па·с.
Процессы, описанные выше, соответствуют только области разрядных промежутков озонатора. После выхода из разрядника в воздушной области остальной установки массоперенос веществ будет связан с процессами диффузии и конвекции
:где:
сО3 diluted – концентрация озона за разрядными промежутками, моль/м3;
JО3 – плотность потока озона, вызванного диффузией, моль/(м2·с);
RO3 – скорость реакции, моль/(м3·с).
Плотность потока озона можно определить через уравнение Фика:
где D – коэффициент диффузии озона, 0,0000157 м2/с.
Для моделирования данных процессов в ПО Comsol Multiphysics были использованы следующие физические интерфейсы: «Plasma», «Turbulent Flow», «Transport of Diluted Species».
В качестве начальных условий в физическом интерфейсе «Plasma» были приняты концентрации поступающих в разрядные промежутки кислорода cO2 и азота cN2 необходимые для расчета концентраций озона соз в соответствии с (1) – (4). Так как в компьютерной модели концентрации озона соз и сО3 diluted определяются в двух разных доменах, то для их сопряжения в интерфейсе «Transport of Diluted Species» на выходных плоскостях разрядного устройства было задано граничное условие (ГУ) соз = сО3 diluted. Таким образом, концентрации озона соз, определяемые внутри разрядных промежутков, являлись начальными значениями для вычислений концентраций озона соз diluted в остальной воздушной области установки. На входе в озонатор, задавалось ГУ «Fan» учитывающее функциональную связь давления p от производительности компрессора Qк. В соответствии с
ГУ «Fan» можно описать следующим образом:где:
n – вектор нормали к задаваемой поверхности;
p0 – давление на входе в установку, Па.
Граничное условие «Outlet», которое учитывает выход смеси из озонатора задавалось уравнением :
где pout – давление на выходе из озонатора, Па.
На основании полученных уравнений, описывающих основные процессы в озонаторе и принятых граничных условий, компьютерную математическую модель процессов в озонаторе можно представить в следующем виде:
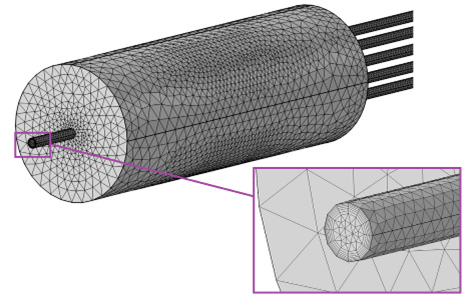
Рисунок 3 - Изображение сетки геометрической модели электроозонатора
3. Результаты исследований и обсуждение
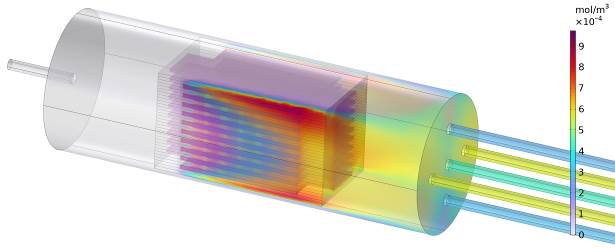
Рисунок 4 - Изображение полей распределения концентраций озона внутри озонатора
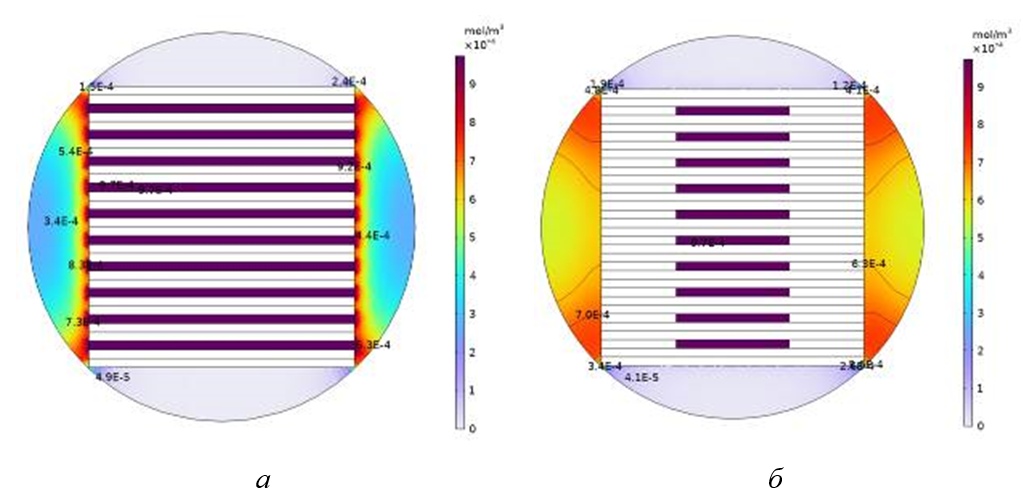
Рисунок 5 - Изображения полей распределения концентраций озона в сечениях: в середине разрядного устройства (а) и на выходе озоновоздушной смеси (б)
4. Заключение
1. Разработана геометрическая модель озонатора для обработки озоном пчелиных ульев, включающая разрядный блок барьерного типа с электродами пластинчатого типа и изолирующий корпус с выходными патрубками.
2. Получено математическое описание основных процессов в озонаторе, включающее выражения основных химических реакций, уравнения переноса массы вещества, функции распределения энергий электронов по Максвеллу и уравнений Навье-Стокса.
3. Разработана компьютерная математическая модель основных процессов, происходящих в озонаторе при его работе, в которой имеются начальные и граничные условия, математические описания процессов и учитываются характеристики компрессора.
4. Результаты анализа реализаций компьютерной математической модели озонатора в ПО Comsol показали, что поле концентраций озона в выходных патрубках неравномерно и может отличаться в 2 раза (от 12,9 мг/м3 до 26,8 мг/м3). Для создания равномерности концентраций озона необходима установка дополнительной конструкции, выравнивающей общую концентрацию озона на выходе из разрядного блока.
5. Используя полученную компьютерную математическую модель озонатора, можно будет проводить коррекцию его геометрии, изменять параметры и режимы с целью получения их оптимальных значений.
