OPTIMIZATION OF QUASILINEAR COMPLICATED SYSTEMS: CASE OF THREE DETERMINED PRIORITIES

Волосатова Т.А.¹, Данекянц А.Г.²

¹ORCID: 0000-0001-6416-0212, Кандидат физ.-мат. наук, Донской государственный технический университет (Ростов-на-Дону), ²ORCID: 0000-0002-0409-0694, Кандидат физ.-мат. наук, Донской государственный технический университет (Ростов-на-Дону)

ОПТИМИЗАЦИЯ КВАЗИЛИНЕЙНЫХ СЛОЖНЫХ СИСТЕМ: СЛУЧАЙ ТРЕХ ДЕТЕРМИНИРОВАННЫХ ПРИОРИТЕТОВ

Аннотация

Данная статья является продолжением исследований математической модели экономической системы, предложенной в работах [1]-[2]. В пространстве Rⁿ заданы три неотрицательные ненулевые непрерывные функции . Существует экономическая система (например, бюджетная организация). Внутренние требования системы выражаются функцией F₃. Экономическая система не является независимой и на нее действуют внешние "оптимизаторы" (например, различные министерства). В данной работе рассмотрена задача с двумя внешними "оптимизаторами". Требования оптимизаторов к системе описываются функциями  F₁ и F₂. Внутренние цели системы и цели "оптимизаторов" в большинстве случаев не совпадают, поэтому функции  естественно рассматривать как разнонаправленные целевые функции. Существует некий арбитр (регулятор), который может влиять как на развитие самой системы, так и на "оптимизаторов". Арбитр заинтересован в плодотворном взаимодействии всех структур. В соответствии с [1–2] мы рассматриваем целевую функцию арбитра вида:, где . Детерминированные показатели a₁,a₂,a₃ называются приоритетами. В рамках предложенной квазилинейной модели получены необходимые условия существования стационарных точек целевой функции и найдена точка локального максимума функции F.

Ключевые слова: локальный максимум целевой функции арбитра, функции квазилинейного вида, детерминированные приоритеты.

Volosatova T.A.¹, Danekyants A.G.²

¹ORCID: 0000-0001-6416-0212, PhD in Physics and Mathematics, Don State Technical University (Rostov-on-Don), ²ORCID: 0000-0002-0409-0694, PhD in Physics and Mathematics, Don State Technical University (Rostov-on-Don)

OPTIMIZATION OF QUASILINEAR COMPLICATED SYSTEMS: CASE OF THREE DETERMINED PRIORITIES

Abstract

This paper is prolongation of researches of mathematical model of the economic system offered in works [1] - [2]. In space Rⁿ three nonnegative nonzero continuous functions are set. There is an economic system (for example, the state enterprise). Function F₃ describes interior requirements of the system. The economic system is dependent on external “optimizers” (for example, the various ministries). The problem with two exterior "optimizers" is considered in this work. “Optimizer’s” system requirements are described by functions F₁ and F₂. Interior purposes of the system and “optimizers” does not match in most cases, therefore is considered as multidirectional target functions. There is a certain arbiter (governor) who can influence both the system development, and “optimizers”. The arbiter is interested in productive interaction of all structures. According to [1-2] we consider target arbiter function type: , where  and . The determined indicators a₁,a₂,a₃ are called as priorities. Required stationary points conditions of target function and function F  local maximum are determined within the limits of the offered quasilinear model.

Keywords: local maxima of target function of the arbiter, function of the quasilinear aspect, the determined priorities.

В пространстве Rⁿ рассмотрим неотрицательные ненулевые непрерывные функции , дважды непрерывно дифференцируемые на открытых множествах  соответственно, где i=1,2,3. При этом , а через  обозначаем в дальнейшем их дополнения. Функции , будем интерпретировать как разнонаправленные целевые функции. Целевая функция  выражает внутренние требования системы, а функции F₁ и F₂ формулируют требования некоторых внешних “оптимизаторов” к этой системе. Построим новую целевую функцию арбитра

  (1)

показатели которой удовлетворяют условиям:  и . В дальнейшем, показатели a₁,a₂,a₃ будем называть приоритетами. Умножение в формуле (1) предполагает, что арбитр, оказывая влияние на внутреннюю структуру системы и на внешних “оптимизаторов”, стремится обеспечить эффективную работу всей системы, то есть максимизировать целевую функцию F.

Исходя из вышеизложенного, считаем, что , то есть принимаем в рассмотрении только ситуации, когда существуют точки локальных и глобальных максимумов функции F. Если , то , то есть такие точки являются точками глобального минимума функций F. Будем предполагать, что F_i являются функциями «квазилинейного» вида:

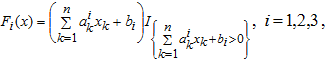  (2)

где  есть индикатор множества A.

Найдем частные производные функций . При этом будем использовать обозначения

  (3)

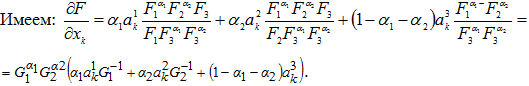
Из того, что , и из условий (2) вытекает, что  . Таким образом, существование точки , в которой  при всех , равносильно выполнению следующего условия:

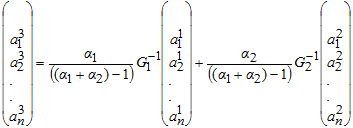  (4)

В стационарной точке  функции  и . С учетом того, что  принимают фиксированные значения, из формулы (4) вытекает, что существование стационарной точки  равносильно линейной зависимости системы векторов .

Введем обозначения , тогда , .

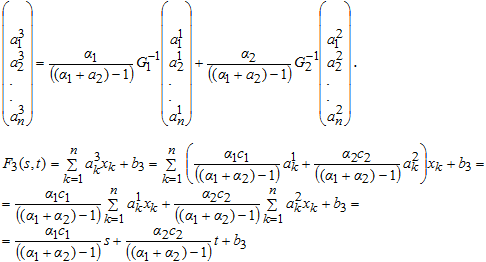В стационарной точке имеем: Тогда 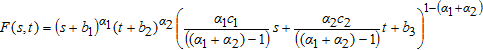  (5) Исследуем функцию F(s,t) на экстремум.

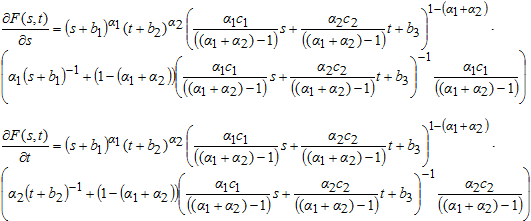
Таким образом, в стационарной точке , с учетом условий (2), необходимое условие экстремума функции F(s,t)  будет иметь вид:

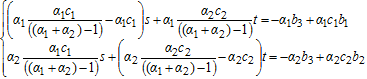  (6)

Определим, имеет ли система (6) решение. Вычислим главный определитель системы.

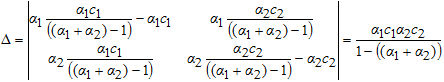
Так как приоритеты ,  и константы , то , значит система (6) имеет единственное решение. Решаем систему (6) и находим критическую точку M(s,t) функции F(s,t).

  (7)

Определим, является ли стационарная точка M(s,t) точкой экстремума. Найдем частные производные второго порядка:

В точке

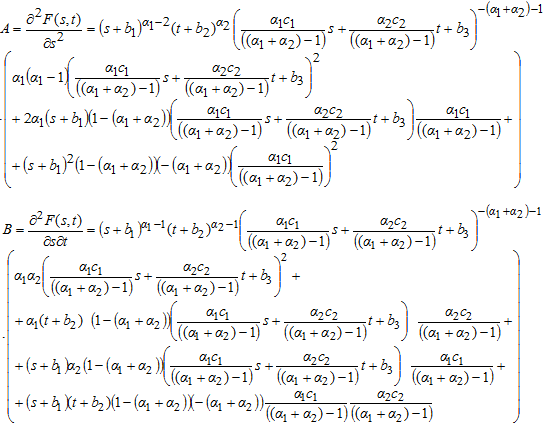
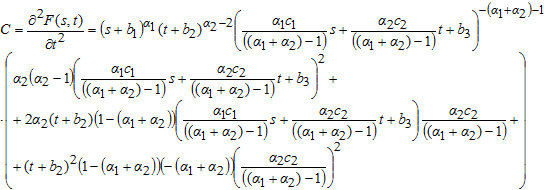
функция  достигает своего локального максимума, если в этой точке выполняются следующие условия: .

Проверим, что .

Так, как , то первые три множителя строго больше 0. Исследуем знак выражения:

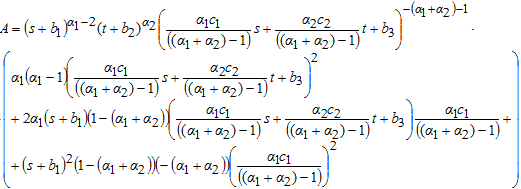
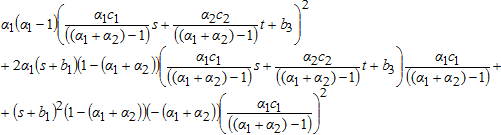
В данном выражении первое слагаемое отрицательное, т.к. , второе слагаемое отрицательное, так как только множитель , и третье слагаемое отрицательное, так как только множитель . Значит, A < 0, в любой точке.

Определим знак выражения . В стационарной точке М выполняются равенства (6), из которых получаем:

Тогда

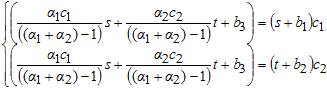
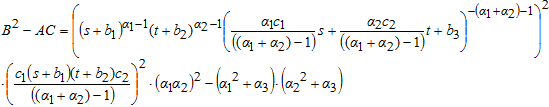
Первый и второй множители в произведении строго положительны, исследуем знак третьего множителя. Так как , получаем , откуда следует, что <0.

Таким образом, мы доказали, что точка  − точка локального максимума функции F(s,t).

Итак, нами доказана следующая

ТЕОРЕМА. Для того, чтобы функция , заданная равенством (1)-(3), имела стационарные точки, необходимо, чтобы система векторов  была линейно зависима и выполнялось равенство

Обратно, пусть эти условия выполнены. Введем обозначения . Тогда целевая функция F примет вид (5). Исследуемая функция F(s,t) имеет локальный максимум в точке .

Доказанная теорема, показывает, что рассматриваемая в работе экономическая система может функционировать с оптимальной отдачей, если есть арбитр, который жестко расставляет приоритеты, основываясь на актуальных данных. Но надо понимать, что ситуации, возникающие в системе, могут трактоваться экспертами не однозначно, данные предоставленные разными сторонами арбитру могут существенно различаться и сам арбитр может иметь личные предпочтения. Поэтому в дальнейших исследованиях, логично предположить, что приоритеты − это случайные величины. Также следует рассмотреть модель с большим числом приоритетов.

Данная работа выполнена при поддержке РФФИ (грант № 16-01-00184а).

Литература

1. Вагин В.С., Павлов И.В. Оптимизация квазилинейных моделей сложных систем с учетом вероятностного характера приоритетов. // Сборник тезисов Международной конференции «XXVI Крымская осенняя математическая школа-симпозиум по спектральным и эволюционным задачам». – Симферополь, 2015. – С. 109.
2. Вагин В.С., Павлов И.В. Моделирование и оптимизация квазилинейных сложных систем с учетом вероятностного характера приоритетов. // Научно-технический журнал «Вестник РГУПС» –Ростов-на-Дону, 2016. №1(61). – С. 135-139.
3. Волосатова Т.А., Данекянц А.Г. Оптимизация квазилинейных сложных систем с тремя приоритетами. // Сборник тезисов Международной научной конференции «Современные методы и проблемы теории операторов и гармонического анализа и их приложения VI» – Ростов-на-Дону, 2016. – С. 132.

References

1. Vagin V.S., Pavlov I.V. Optimizacija kvazilinejnyh modelej slozhnyh sistem s uchetom verojatnostnogo haraktera prioritetov [Optimization of quasi-linear models of complicated systems with using random nature of priorities]. // Sbornik tezisov Mezhdunarodnoj konferencii «XXVI Krymskaja osennjaja matematicheskaja shkola-simpozium po spektral'nym i jevoljucionnym zadacham». –2015. – S. 109. [in Russian]
2. Vagin V.S., Pavlov I.V. Modelirovanie i optimizacija kvazilinejnyh slozhnyh sistem s uchetom verojatnostnogo haraktera prioritetov [Modeling and optimization of quasi-linear models of complete systems with using random nature of priorities]. // Nauchno-tehnicheskij zhurnal «Vestnik RGUPS» [Scientific and Technical Journal «Vestnik RGUPS»]. – Rostov-na-Donu, 2016. #1(61). – S. 135-139. [in Russian]
3. Volosatova T.A., Danekjanc A.G. Optimizacija kvazilinejnyh slozhnyh sistem s tremja prioritetami [Optimization of quasi-linear complicated systems with three priorities]. // Sbornik tezisov Mezhdunarodnoj nauchnoj konferencii «Sovremennye metody i problemy teorii operatorov i garmonicheskogo analiza i ih prilozhenija VI» [The collection of theses of the Sixth International Scientific Conference "Modern Methods, Problems and Applications of Operator Theory and Harmonic Analysis VI"] – Rostov-na-Donu, 2016. – S. 132. [in Russian]