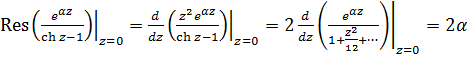INTEGRALS OF THE ELECTRON GAS MODELS

Аринштейн Э.А.

Доктор физико-математических наук, профессор, Тюменский государственный университет

ИНТЕГРАЛЫ МОДЕЛИ ЭЛЕКТРОННОГО ГАЗА

Аннотация

Приведен простой способ прямого вычисления интегралов, используемых в моделях теории металлов, их значения обычно  берутся из таблиц. Изложенный метод может оказаться полезным методическим приемом.

Ключевые слова: электронный газ, модели, интегралы.

Arinstein E.A.

PhD in Physics and Mathematics, Professor, Tyumen State University

INTEGRALS OF THE ELECTRON GAS MODELS

Abstract

We offer a simple way of the direct calculation of the integrals used in models of the theory of metals, usually their values are taken from the tables. The above method may be useful instructional technique.

Keywords: electron gas, models, integrals

 

При анализе теплоемкости и ряда других свойств металлов используется модель электронного газа или электронной жидкости [1-4]. (Существует обширная литература по статистической физике и физике твердого тела кроме указанных, весьма удачных учебников.) При этом возникает необходимость вычисления интегралов вида

,

где энергия E – функция квазиимпульса электрона,  – уровень Ферми, ,  температура T выражена в энергетических единицах. В большинстве случаев при обычных и низких температурах , подинтегральное выражение очень быстро, экспоненциально убывает, оно практически равно нулю при , и поэтому нижний предел –μ/T  интеграла по x можно заменить на –∾ (см. примечание).

Разложение  сводит задачу к вычислению интегралов вида  индекс n –целый, неотрицательный. Значение этих интегралов обычно выражается через табличные значения дцэта-функции Римана .

Приведем простой способ их прямого вычисления, который не используется в приведенных (и других) учебниках и может оказаться полезным методическим приемом.

Интеграл    содержит все  и при  сходится абсолютно. Расмотрим контурный интеграл  в комплексной плоскости. Контур состоит из действительной оси , прямой обратного направления, параллельной действительной оси: z=x+2πi,   и двух отрезков,  замыкающих контур: z=x+iy, 0<y<2π,  x , интегрирование по этим отрезкам дает вклад, равный нулю. Внутри контура подинтегральная функция имеет полюс второго порядка при z=iπ. По теореме о вычетах

,

.  В итоге получим

 .

Это разложение определяет все . Очевидно, что все .

Интеграл  определяет коэффициент в выражении для линейной зависимости теплоемкости электронного газа от температуры. Интеграл  определяет значение добавки к Дебаевскому выражению для колебательной теплоемкости  при ,  – характеристическая Дебаевская температура. Интеграл   выражается через     – сумма членов при четных n,  – сумма членов при нечетных n.   В то же время  

Так как , то  

Электронная добавка к теплоемкости порядка обычно в учебниках не рассматривается, как малая по сравнению с Дебаевским выражением.

Возможно применение рассмотренного метода при анализе и других моделей, использующих свойства Ферми- и Бозе-газов.

Примечание.  Погрешность вычисления контурного интеграла, возникающая  при замене нижнего предела –μ/T на –∾, равна интегралу   по отрезку, замыкающему контур, при этом модуль подинтегрального выражения равен .  Это дает достаточно простую оценку погрешности.

Литература

1. Л. Д. Ландау, Е. М. Лифшиц. Статистическая физика, часть 1. Москва, «Наука», ФМЛ,1976 г. 584 стр. (и другие издания).
2. Ч. Киттель. Введение в физику твердого тела. Москва, «Наука», ФМЛ, 1978 г.,792 стр.
3. Дж. Займан. Принципы теории твердого тела. «МИР», Москва, 1974 г., 472 стр.
4. А. А. Абрикосов. Основы теории металлов. Москва, «Наука», ФМЛ, 1987г. , 520 стр.

References

1. D. Landau, E. M. Lifshits. Statistical Physics, Part 1. Moscow,  “Nauka“, FML, 1976, 584pp.
2. Charles Kittel. Introduction to Solid State Physics. Fourth Edition. John Wiley and Sons, Inc. New York, London,Sydney,Toronto 1976
3. M. Ziman. Principles of the Theory of Solids. Cambridge at the university press. 1972.
4. A. Abricosov. Bases of the Metal Theory. Moscow, “Nauka“, FML, 1987.