Journals
Submit manuscript Sign in / Sign up
Advanced search
Article sections
Review

Electrical resistance of binary antiferromagnetic alloys

Research article
Borodin K. I.
Volkov V. A.
DOI:
https://doi.org/10.60797/IRJ.2025.160s.28
Issue: № 10 (160) S, 2025
Suggested:
14.08.2025
Accepted:
20.08.2025
Published:
24.10.2025
168
0
XML
PDF

Abstract

The electrical resistance of antiferromagnetic alloys is calculated in the coherent potential approximation. It is shown that if the Fermi energy is localised near the gap in the electron density of states, the electrical resistance can increase with increasing magnetisation of the sublattices. Experimental studies previously conducted on Cr-Pt alloys show that the resistance anomaly increases with increasing impurity concentration. For Ni-Mn alloys of equiatomic composition, a significant increase in electrical resistance (over 80%) was previously observed experimentally during the transition to the AFM state. Thus, the theory we propose provides a qualitative explanation for the observed temperature and concentration anomalies in the electrical resistance of AFM alloys.

Keywords:
residual resistivity ratio, antiferromagnetic alloys, coherent potential approximation.

1. Введение

Как известно, при атомном упорядочении бинарных и тройных немагнитных сплавов происходит перестройка электронного спектра. Для некоторых (но не для всех!) сплавов электросопротивление 

 вблизи температуры перехода порядок-беспорядок обнаруживает аномалию: возрастание при увеличении параметра дальнего порядка с последующим падением при дальнейшем увеличении последнего
,
,
. Причем эта особенность в поведении электросопротивления связывается именно с развитием дальнего порядка, т.к. в неупорядоченном состоянии подобная аномалия не обнаруживается. Объяснение данной аномалии было дано в работах
,
,
, в которых электросопротивление упорядочивающихся сплавов вычислялось с учетом изменений электронного спектра при упорядочении. В результате была выявлена возможность немонотонного изменения остаточного электросопротивления со степенью дальнего порядка в случае, когда поверхность Ферми проходит вблизи поверхности разрыва в спектре. Поскольку при переходе сплава в антиферромагнитное (АФМ) состояние также происходит перестройка электронного спектра, обусловленная появлением магнитных (а не структурных) подрешеток, в таких системах также возможны аналогичные аномалии остаточного электросопротивления. Подобные аномалии наблюдались для ряда  АФМ сплавов экспериментально
,
,
.

В данной работе выполнен теоретический расчет высокотемпературного (

 — температура Нееля) электросопротивления бинарных АФМ сплавов А-В с ПК или ОЦК решеткой, обусловленного неоднородностями спиновой системы и статическим потенциалом нерегулярного распределения атомов разных сортов по решетке. Спиновая система описывается в рамках 
 обменной модели. В
было показано, что такой сплав может быть антиферромагнитным либо в неупорядоченном, либо в полностью упорядоченном (при стехиометрическом составе) состояниях. Поэтому рассмотрим структурноразупорядоченный сплав произвольного состава. Полагаем, что при АФМ упорядочении в нем реализуется коллинеарная двухподрешеточная магнитная структура, появление которой изменяет периодичность внутреннего поля системы и приводит к необходимости использования двухподрешеточного варианта приближения когерентного потенциала (ПКП) даже для структурно разупорядоченного сплава
.

2. Остаточное электросопротивление бинарных антиферромагнитных сплавов

Предполагая, как это обычно делается в ПКП, что энергии электронного переноса между различными узлами не зависят от состава сплава, и используя 

 обменную модель для описания взаимодействия электронов проводимости с системой локализованных спинов, запишем гамильтониан сплава в предcтавлении Ваннье 

(1)

В этой формуле 

 — операторы рождения и уничтожения электрона со спином 
 на узле 
 — радиус-векторы узлов 
 - й подрешетки; 
\varepsilon_{\vec{n}}$ и $I_{\vec{n}}
 — энергия атомного уровня и интеграл 
 обмена для узла 
 , принимающие соответственно значения 
\varepsilon_\alpha$ и $I_\alpha
  в зависимости от сорта атома, занимающего этот узел, 
 — операторы локализованного на узле 
 спина; t — интеграл переноса между ближайшими соседями; штрих у суммы во втором слагаемом в (1) означает, что суммирование ведется по узлам 
 и 
, являющимся ближайшими соседями. При выводе Н считалось, что локализованные спины всех компонент имеют величину S = 1/2 и связаны эффективным прямым обменом.

Имея в виду использование одноузельного варианта ПКП

,
, представим H в виде 

H=H_0+\sum_{\vec{n}} V_{\vec{n}}$,
(2)

где 

(3)
(4)

В соответствии со сверхструктурой АФМ сплава введем оператор когерентного потенциала 

(5)

через который выразим эффективный гамильтониан сплава

(6)

и соответствующую ему одноэлектронную функцию Грина 

\widetilde{G}(z)=(z-\widetilde{H}(z))^{-1}, F_l(z)=<\vec{n}_l|\widetilde{G}(z)| \vec{n}_l>
(7)

Условие самосогласования одноузельного ПКП, из которого находится оператор когерентного потенциала, состоит в равенстве нулю усредненной t -матрицы рассеяния 

-го узла
,
. В силу неэквивалентности подрешеток АФМ сплава таких уравнений будет два
 

\ll\left(V_{\vec{n}_l}-\sum_{\vec{n}_l}\right)\left[1-\tilde{G}(z)\left(V_{\vec{n}_l}-\sum_{\vec{n}_l}\right)\right]^{-1}>_T>=0
(8)

Здесь символ  означает тепловое усреднение в системе локализованных спинов при фиксированной конфигурации атомов в сплаве, которое далее проводится в приближении молекулярного поля, а символ <...> означает усреднение по всем возможным  конфигурациям при заданном значении  концентрации компоненты А. Для случайной одноузельной величины 

&lt;f_{\vec{n}_l}&gt;=\sum_{\alpha=A, B} c_\alpha f_\alpha=\bar{f}
(9)

При вычислении тепловых средних в системе локализованных спинов для АФМ сплава запишем

&lt;S_{\tilde{n}_l}^Z&gt;_T=(-1)^l S \mu
(10)

где 

 — относительная намагниченность подрешетки. Решая систему (8) методом итераций, получим в приближении виртуального кристалла (первая итерация) 

(11)

Тогда плотность электронных состояний 

 в пределе виртуального кристалла будет 

(12)

Таким образом и в антиферромагнитных сплавах и в чистых антифер-ромагнетиках при 

T&lt;T_N
 в 
 появляется щель ширины 
, центрированная на 
. Это является следствием изменения периода внутреннего поля кристалла при антиферромагнитном упорядочении.

В пределе слабого рассеяния (вторая итерация) недиагональные по спину матричные элементы когерентного потенциала равны нулю, а диагональные могут быть записаны в виде

(13)
(14)
(15)
F_l(z)=2\left(z-\bar{\varepsilon}-(-1)^l \bar{I} S \mu\right)\left\{1-\sqrt{1-\frac{1}{(z-\bar{\varepsilon})^2-(\bar{I} S \mu)^2}}\right\}, l=1,2$,
(16)
\delta_{\varepsilon}=\varepsilon_A-\varepsilon_B, \quad \delta_I=I_A-I_B, S^2 \Delta^2=&lt;\left(S_{\vec{n}}^Z\right)^2&gt;_T
(17)

Тензор статической электропроводности сплава определяется по формуле Кубо-Гринвуда

 

\lambda^{\alpha \beta}=\frac{\pi e^2 h}{N \Omega} \int d E\left(-\frac{\partial f}{\partial E}\right) S p \ll v^\alpha \delta(E-H) v^\beta \delta(E-H)&gt;_T&gt;
(18)

где 

 — заряд электрона; 
 — объем, приходящийся на один атом, 
 — функция Ферми; 
 — компонента оператора скорости; N — число узлов решетки сплава,
 — постоянная Планка. 

Формулу (18) можно записать в виде 

(19)

где

(20)

Поскольку величины, входящие в (20), являются трансляционно-инвариантными, вычисляем шпур в блоховском базисе. Используя для получающейся при этом суммы по 

 аппроксимацию, соответствующую полуэллиптической модели плотности состояний, получим выражение для статической проводимости  в пределе слабого рассеяния
.

В этом случае проводимость будет отлична от нуля тогда, когда энергия Ферми сплава попадает в интервал 

|\bar{I} S \mu|&lt;\left|\varepsilon_F-\bar{\varepsilon}\right| \leq \sqrt{1+(\bar{I} S \mu)^2}
(21)

и результаты будут существенно зависеть от локализации энергии Ферми относительно щели.

3. Основные результаты и их обсуждение

Если энергия Ферми расположена вдали от щели, электросопротивление антиферромагнитного сплава есть

\rho=\lambda^{-1}=\frac{\rho_0}{1-\left(\varepsilon_F-\bar{\varepsilon}\right)^2}\left[c_A c_B \delta_{\varepsilon}^2+\overline{I^2} S(S+1)-(\bar{I} S \mu)^2\right], \rho_0=\frac{3 \pi \Omega}{e^2 h v_m^2}$,
(22)

 

 — максимальная скорость.

Видно, что сопротивление является линейно-квадратичной функцией состава, и переход в антиферромагнитное состояние, сопровождающийся увеличением спонтанной намагниченности подрешеток, приводит к уменьшению 

\rho$.

Если энергия Ферми находится вблизи от щели, сопротивление описывается более сложным выражением

(23)

где 

\rho_1=\rho_0 \overline{I^2} S(S+1)$,
(24)
(25)
\rho_3=\rho_0\left(2 \overline{I^2} S^2 \Delta^2+4 c_A c_B S \frac{\delta_{\varepsilon} \delta_I}{\tau}\right) \frac{\tau^2 \mu^2}{1-\tau^2 \mu^2},|\tau|&lt;1$.
(26)

Отметим, что выражения (22)-(26) получены в приближении, сохраняющем наибольший член разложения по параметрам рассеяния.

В парамагнитной области (

T&gt;T_N, \mu=0
) находим из (23)-(26)

(27)

В этом случае сопротивление является суммой вкладов от упругого спинового рассеяния и упругого примесного рассеяния.

Изменение 

 в зависимости от намагниченности подрешетки показано на Рис. 1 для ряда значений параметров 
 и 
. Как видно из этих кривых, при некоторых значениях параметров возможен рост 
 при увеличении 
, т.е. при понижении температуры. Кривые 2, 3, 4, 6 дают примеры немонотонной зависимости 
 от намагниченности подрешетки. Подобное поведение 
 в совокупности с фононным вкладом в сопротивление может быть причиной аномалии температурной зависимости электросопротивления  АФМ сплава.

В отличие от 

слагаемое 
монотонно зависит от температуры. Если выражение в скобках в (26) положительно, 
возрастает при увеличении 
(т.е. при уменьшении температуры). Такое поведение 
будет усиливать аномалию температурной зависимости полного сопротивления.

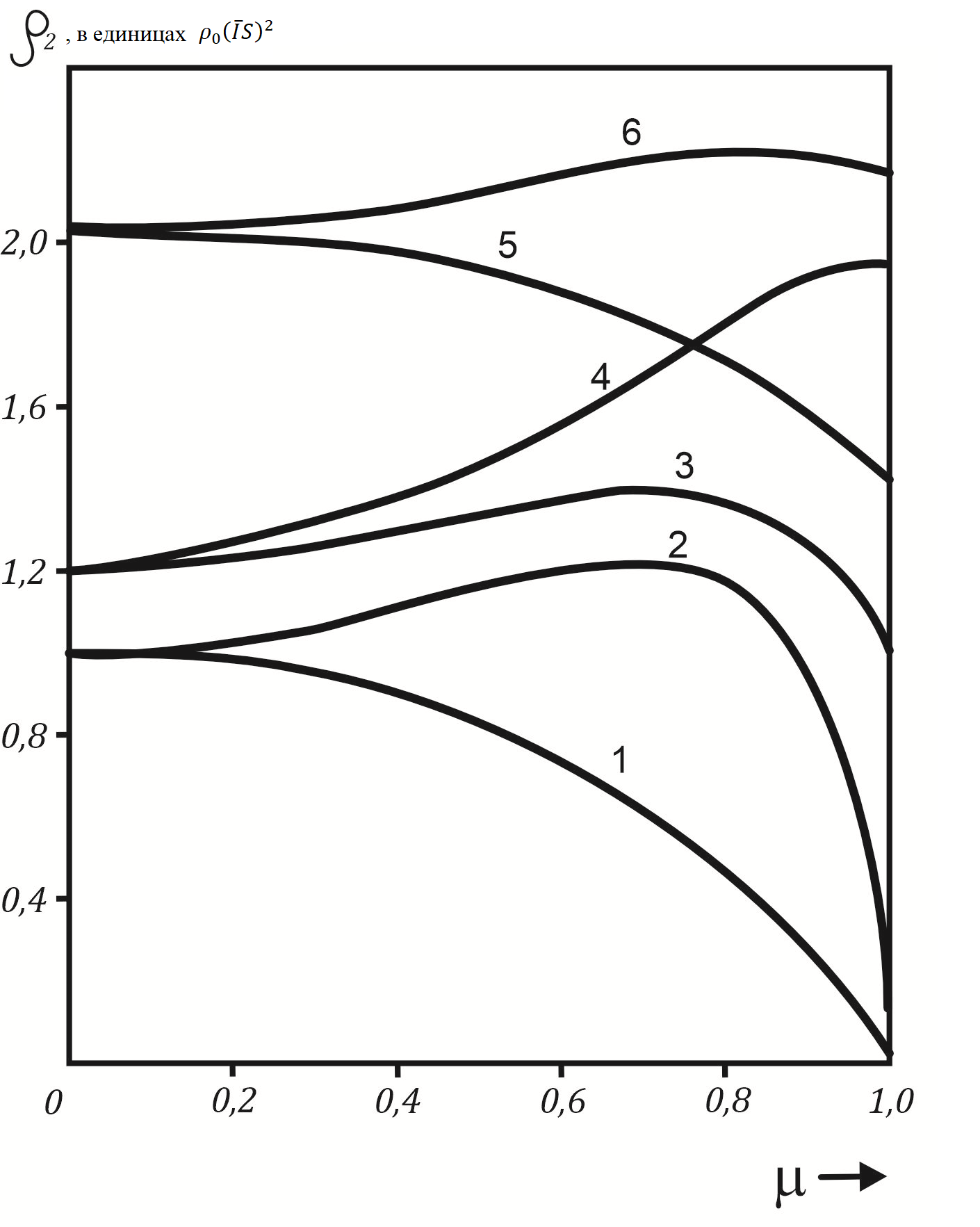
Зависимость p2 от намагниченности подрешетки для различных значений параметров |τ| и a: (1) |τ|=0,4, a=1; (2) |τ|=0,9, a=1; (3) |τ|=0,8, a=1,2;(4) |τ|=0,9, a=1,2; (5) |τ|=0,4, a=2; (6) |τ|=0,6, a=2

Рисунок 1 - Зависимость p2 от намагниченности подрешетки для различных значений параметров |τ| и a:

(1) |τ|=0,4, a=1; (2) |τ|=0,9, a=1; (3) |τ|=0,8, a=1,2;

(4) |τ|=0,9, a=1,2; (5) |τ|=0,4, a=2; (6) |τ|=0,6, a=2

DOI:10.60797/IRJ.2025.160s.28.1

Концентрационная зависимость слагаемого

приведена на Рис. 2 для случая 
. Когда параметр 
b&lt;0,\left(b=\frac{4 \delta_{\varepsilon} \delta_I}{I_A^2 \tau}\right)
 и достаточно велик по абсолютной величине, член
может изменить свой знак в области больших концентраций. Ясно, что в этом случае аномалия в сопротивлении сплава будет уменьшаться вплоть до полного исчезновения, когда состав сплава будет стремиться к эквиатомному. Если же b>0, то в концентрированных сплавах аномалия сопротивления за счет слагаемого
будет возрастать.

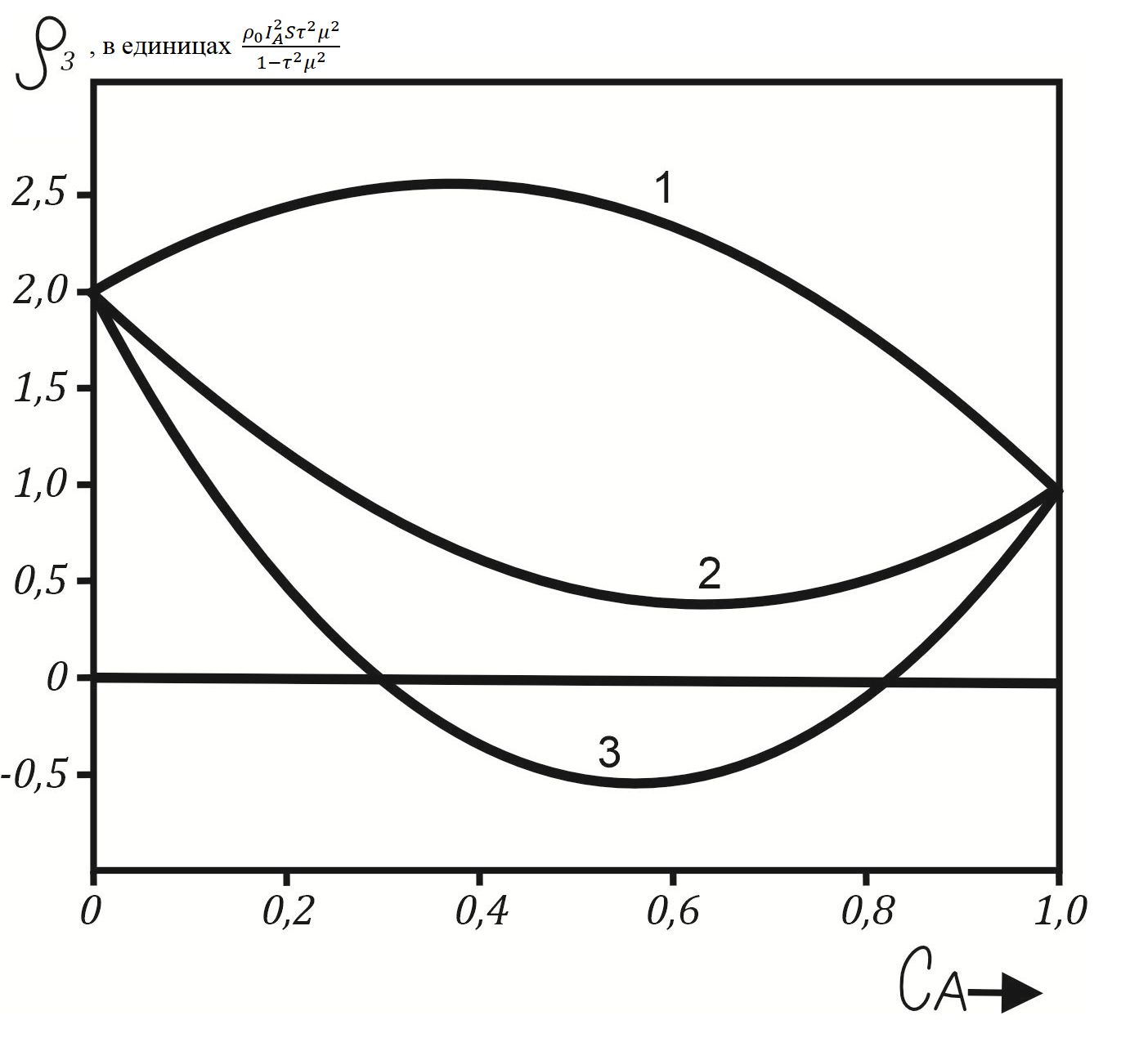
Концентрационная зависимость ρ3 для ряда значений параметра b: (1) b= 4; (2) b= - 4; (3) b= - 8

Рисунок 2 - Концентрационная зависимость ρ3 для ряда значений параметра b:

(1) b= 4; (2) b= - 4; (3) b= - 8

DOI:10.60797/IRJ.2025.160s.28.2

4. Заключение

Экспериментальные исследования

, проведенные для сплавов Cr-Pt, показывают, что при возрастании концентрации примеси аномалия сопротивления увеличивается. В
для сплавов Ni-Mn эквиатомного состава было обнаружено значительное увеличение электросопротивления (свыше 80%) при переходе в АФМ состояние. В свете изложенной теории представляется возможным связать эти факты с вкладом слагаемого
в общее электросопротивление (в случае b > 0).

Таким образом, изучение примесного и спинового рассеяния позволяет качественно объяснить наблюдавшиеся температурные и концентрационные аномалии электросопротивления АФМ сплавов.

Additional materials

Not specified

Financing

Авторы не получали финансовой поддержки для проведения исследования, написания и публикации статьи

Acknowledgements

Not specified

Conflicts of interests

Not specified

References

  • Tuxfatullin A.A.

    Ob anomal'nom izmenenii e'lektrosoprotivleniya pri uporyadochenii splavov tipa Mg3Cd
    [
    On the anomalous change in electrical resistance during the ordering of Mg3Cd type alloys
    ] / A.A. Tuxfatullin, M.B. Makogon, R.M. Tuxfatullina //
    Izvestiya vuzov. Fizika
    [
    Proceedings of Universities. Physics
    ]. — 1968. — 5. — P. 50–53. [in Russian]

  • Pal'guev E.V.

    Anomal'naya temperaturnaya zavisimost' e'lektrosoprotivleniya uporyadochivayushhixsya splavov palladij-zhelezo
    [
    Abnormal temperature dependence of electrical resistance of ordered palladium-iron alloys
    ] / E.V. Pal'guev, A.A. Kuranov, P.N. Syutkin et al. //
    Fizika metallov i metallovedenie
    [
    Metal physics and metal science
    ]. — 1976. — 1. — P. 57–62. [in Russian]

  • Karpov Yu.G. Vliyanie atomnogo uporyadocheniya na magnitnie svoistva i elektrosoprotivlenie splava Fe25Pd50Au25 [The effect of atomic ordering on the magnetic properties and electrical resistance of Fe25Pd50Au25 alloy] / Yu.G. Karpov, F.A. Sidorenko, V.V. Slobodenyuk // Fizika metallov i metallovedenie [Metal Physics and Metal Science]. — 1979. — 3. — P. 498–504. [in Russian]

  • Masharov S.I.

    Vliyanie izmeneniya e'lektronnogo spektra pri uporyadochenii na e'lektrosoprotivlenie binarny'x splavov
    [
    The effect of changes in the electronic spectrum during ordering on the electrical resistance of binary alloys
    ] / S.I. Masharov, N.M. Ry'balko //
    Fizika metallov i metallovedenie
    [
    Metal Physics and Metal Science
    ]. — 1975. — 6. — P. 1133–1143. [in Russian]

  • Borodachev S.M.

    Ostatochnoe soprotivlenie binarny'x uporyadochivayushhixsya splavov (priblizhenie kogerentnogo potenciala)
    [
    Residual resistance of binary ordered alloys (approximation of coherent potential)
    ] / S.M. Borodachev, V.A. Volkov, S.I. Masharov //
    Fizika metallov i metallovedenie
    [
    Metal Physics and Metal Science
    ]. — 1976. — 6. — P. 1147–1153. [in Russian]

  • Volkov V.A.

    E'lektrosoprotivlenie trojny'x uporyadochivayushhixsya splavov zameshheniya
    [
    Electrical resistance of triple ordered substitution alloys
    ] / V.A. Volkov, L.P. Zelenin, N.A. Lobasheva //
    Fizika metallov i metallovedenie
    [
    Metal Physics and Metal Science
    ]. — 1989. — 3. — P. 506–511. [in Russian]

  • Marchenkov V.V.

    E'lektrosoprotivlenie, magnitny'e i gal'vanomagnitny'e svojstva litogo i by'strozakalennogo splava Gejslera Mg3Al
    [
    Electrical resistance, magnetic and galvanomagnetic properties of cast and quick-tempered Geisler alloy Mg3Al
    ] / V.V. Marchenkov, V.Yu. Irxin, A.A. Semyannikova //
    Fizika metallov i metallovedenie
    [
    Metal Physics and Metal Science
    ]. — 2023. — 4. — P. 339–345. [in Russian]

  • Arajs S.

    Electrical resistivity and antiferromagnetism of chromium-platinum alloys
    / S. Arajs, K.V. Rao, E.E. Anderson //
    Solid State Communications
    . — 1975. — 3. — P. 331–333.

  • Demidenko V.S.

    Issledovanie osobennostej zonnoj struktury' antiferromagnitnogo soedineniya NiMn
    [
    Investigation of the features of the band structure of the antiferromagnetic compound NiMn
    ] / V.S. Demidenko, A.V. Kolubaev, A.I. Lotkov et al. //
    Fizika metallov i metallovedenie
    [
    Metal Physics and Metal Science
    ]. — 1975. — 5. — P. 1092–1094. [in Russian]

  • Volkov V.A.

    Vliyanie atomnogo i magnitnogo blizhnego poryadka na uporyadochenie binarny'x splavov s OCzK reshetkoj
    [
    Influence of the atomic and magnetic short-range order on the ordering of binary alloys with a BCC lattice
    ] / V.A. Volkov, S.I. Masharov, A.F. Ry'balko et al. //
    Fizika metallov i metallovedenie
    [
    Metal Physics and Metal Science
    ]. — 1985. — 2. — P. 262–274. [in Russian]

  • Volkov V.A.

    E'lektrosoprotivlenie trojny'x uporyadochivayushhixsya ferromagnitny'x splavov
    [
    Electrical resistance of triple ordered ferromagnetic alloys
    ] / V.A. Volkov, A.A. Kuranov, S.I. Masharov et al. //
    Fizika metallov i metallovedenie
    [
    Metal Physics and Metal Science
    ]. — 1979. — 3. — P. 516–523. [in Russian]

  • Velicky B.

    Single site approximation in the electronic theory of simple binary alloys
    / B. Velicky, E. Kirkpatrick, H. Ehrenreich //
    Physical Review
    . — 1968. — 3. — P. 747–766.

  • Velicky B.

    Theory of electronic transport in disordered binary alloys coherent potential approximation
    / B. Velicky //
    Physical Review
    . — 1969. — 3. — P. 614–627.

Review

All articles are peer-reviewed. But the reviewer or the author of the article chose not to publish a review of this article in the public domain. The review can be provided to the competent authorities upon request.

Author information

AffiliationM. N. Mikheev Institute of Metal Physics, Ural Branch of the Russian Academy of Sciences, Ekaterinburg, Russian Federation
Role:Author, Data curation, Software, Approbation, Visualization, Writing, reviewing and editing, Analysis, Project administrator
ORCID:0000-0001-5536-4256
AffiliationUral Federal University, Ekaterinburg, Russian Federation
Role:Author, Conceptualization, Methodology, Management, Writing, reviewing and editing, Draft writing and preparation, Research data analysis, Analysis
ORCID:0000-0002-7955-959X

Article metrics

Views:168
Downloads:0
Views
Total:
Views:168