Modernization of the classical model for determining surface dynamic viscosity based on integrated signal processing of an oscillating droplet

Поверхностная динамическая вязкость (ПДВ) является ключевым реологическим параметром, определяющим устойчивость межфазных слоев к деформации и играющим решающую роль в формировании и стабилизации пен, эмульсий и других дисперсных систем. Ее точное определение особенно актуально для биополимеров, таких как хитозан (ХТЗ), широко применяемых в пищевой, фармацевтической и косметической промышленности благодаря выраженным поверхностно-активным свойствам

На сегодняшний день наиболее распространенным методом измерения ПДВ является метод осциллирующей капли, реализованный в современных тензиометрах (DSA100, PAT-1 и др.)

Однако существующая методология имеет принципиальный недостаток: она предполагает идеально гармонический характер колебаний и основывается только на двух экстремальных значениях за период, что делает результаты чувствительными к шуму и искажениям сигнала. В реальных экспериментах колебания площади капли часто сопровождаются систематическими отклонениями от идеальной синусоиды, что приводит к ошибкам в расчете ПДВ, особенно при исследовании полимерных растворов, где возможны асимметрия сигнала и наличие высших гармоник

Большинство коммерческих систем и научных публикаций по-прежнему используют упрощенный подход, игнорирующий форму всей кривой колебаний. Хотя отдельные исследования указывают на преимущества интегральных методов

Целью настоящей работы является повышение точности ПДВ вязкости путем модернизации классической модели Люкассена–ван ден Темпеля на основе интегрального анализа полного периода колебаний и метода наименьших квадратов (МНК).

Для достижения цели решались следующие задачи:

1. Разработка математической модели обработки сигнала осциллирующей капли на основе метода наименьших квадратов.

2. Сравнительный анализ точности классического и предложенного методов на примере 0,5% раствора хитозана.

3. Определение частотной зависимости поверхностной динамической вязкости и идентификация резонансной частоты адсорбированного слоя.

В работе представлена модификация методологии определения относительной деформации на основе интегрального представления и метода наименьших квадратов

1. Точное определение амплитуды деформации на основе анализа всего периода колебаний.

2. Снижение влияния случайных помех за счет усреднения.

3. Объективную оценку степени гармоничности колебаний.

4. Повышение точности определения поверхностной динамической вязкости на 30–50% по сравнению с традиционным методом

Метод реализован на установке DSA 100 и протестирован на 0,5 % растворе ХТЗ при частотах от 0,25 до 1,0 Гц. Полученные результаты демонстрируют нелинейную зависимость ПДВ от частоты с четко выраженным максимумом при 0,33 Гц, что соответствует резонансной частоте адсорбированного слоя ХТЗ

Актуальность исследования обусловлена необходимостью повышения точности определения ПДВ для разработки стабильных пен и эмульсий в пищевой и фармацевтической промышленности

Исследование ПДВ проводилось методом осциллирующей капли с использованием реологического модуля, оснащенного пьезоэлектрическим приводом и системой оптической регистрации на базе CCD-камеры (25 кадров/с). Капля раствора ХТЗ 0,5% формировалась на кончике капилляра из нержавеющей стали диаметром 1,82 мм. Деформация межфазной границы осуществлялась путем периодического изменения объема капли с заданным периодом Т = 1, 2, 3, 4 с и амплитудой смещения насоса 1,0 мм. Температура поддерживалась на уровне 30 °C, плотность раствора составляла ρ = 0,9985 г/см³.

Форма капли в каждый момент времени фиксировалась с частотой 25 Гц, после чего проводилась обработка изображений с применением программного обеспечения, основанного на решении уравнения Юнга—Лапласа. На основе профиля капли рассчитывались текущие значения площади поверхности A(t), периметра, радиуса кривизны в экваториальной области R(t) и мгновенного угла смачивания θ(t). ПН σ(t) определялось по распределению давления вдоль профиля капли.

Оценка ПДВ выполнена двумя способами: на основе классической модели Ж. Люкассена (J. Lucassen) и предложенной модифицированной интегральной формулой, реализуемой МНК.

В современных автоматизированных системах анализа поверхностно-динамических свойств, разработанных такими компаниями, как KRÜSS и Biolin Scientific, расчет дилатационной вязкости доведен до стандартного алгоритмического вида, основанного на анализе гармонических колебаний площади поверхности A(t) и межфазного натяжения σ(t). Данный подход основан на упрощенных выражениях, следующих из модели комплексного дилатационного модуля, предложенной Люкассеном и ван ден Темпелем

где ηs — поверхностная динамическая вязкость, мН·с/м;

σ — ПН, мН/м;

ω — угловая частота, рад/с;

Δφ — фазовый сдвиг между кривыми ПН и площади дилатирующей капли, °;

Δσ — амплитуда изменения ПН, мН/м;

Фазовый сдвиг Δφ между этими сигналами вычисляется как разность фаз, соответствующая временному запаздыванию максимумов. Угловая частота ω = 2πf определяется из заданного периода деформации. Среднее значение σ принимается за характерное натяжение. Данный подход является стандартным для большинства коммерческих установок и широко применяется в литературе. Однако он имеет существенные ограничения: чувствителен к шуму, требует точного определения максимумов, не учитывает нелинейность отклика и предполагает моногармонический характер процесса. При слабом сигнале или высоком уровне помех ошибка в определении Δφ может превышать 20%.

В качестве альтернативы предложена модифицированная интегральная модель, построенная на принципах МНК. В рамках этой модели сигналы A(t) и σ(t) аппроксимируются функциями (2), (3) с последующим расчетом фазового сдвига как Δφ = φσ — φA. Коэффициенты аппроксимации определяются путем минимизации суммы квадратов отклонений между экспериментальными данными и моделью по всему циклу. Такой подход позволяет использовать всю доступную информацию, снижает влияние случайных флуктуаций и повышает устойчивость к ошибкам отдельных кадров.

где A(t) — площадь поверхности капли в момент времени t, в мм²;

σ(t) — ПН в момент времени t, мН/м;

A0 — средняя площадь поверхности (постоянная составляющая), мм2;

σ0 — среднее значение ПН, мН/м;

ΔA — максимальное отклонение площади (амплитуда) от среднего значения A0​, мм2;

Δσ — амплитуда ПН, мН/м;

φA — фазовый сдвиг площади капли,°;

φσ — фазовый сдвиг ПН, °.

Преимущества модифицированной модели определяют следующие факторы:

1. Повышенная точность определения фазового сдвига за счет использования полного массива данных.

2. Устойчивость к локальным искажениям сигнала.

3. Возможность анализа многочастотных режимов.

4. Ввтоматизация обработки без необходимости ручного выбора максимумов.

Недостатки обоих подходов заключаются в предположении о линейной вязкоупругой природе адсорбционного слоя. Классическая модель Люкассена не учитывает возможную зависимость свойств слоя от амплитуды деформации (эффекты нелинейной реологии). Интегральная модель, хотя и более устойчива, также основана на линейной аппроксимации и может давать искаженные результаты при больших деформациях. Кроме того, оба метода чувствительны к корректности определения геометрии капли, особенно в условиях значительной дилатации.

Для верификации результатов использовались данные по чистому глицерину (99,98%, плотность 1,261 г/см³, температура 25 °C), полученные при аналогичных условиях (T = 0,5 с, амплитуда насоса 0,9–1,0 мм). Соответствие данных, полученных двумя методами, подтверждает, что предложенная модификация формулы сохраняет физическую адекватность и может использоваться для обработки экспериментальных данных. В рамках исследования поверхностно-динамических свойств водных растворов полимеров были применены два метода расчета дилатационной вязкости: классический амплитудный и модифицированный интегральный. В качестве модельных систем использовались растворы ХТЗ концентрацией 0,5% и чистый глицерин при температуре 25 °C. Эксперименты проводились методом осциллирующей капли с использованием автоматизированного тензиометра, где периодическая деформация капли вызывалась пьезоэлектрическим насосом с заданной частотой (f = 0,25—1,0 Гц).

Классический метод основан на определении амплитудных значений и перепада межфазного натяжения Δσ, рассчитываемых по экстремальным точкам колебательного процесса (формулы (4)—(7)).

Альтернативно, разработана и верифицирована математическая модель, использующая интегральное представление деформации. В ее основе лежит среднеквадратичная оценка отклонения площади поверхности за один период колебаний.

Сравнение этих показателей для раствора ХТЗ и глицерина показало расхождение в диапазоне 16–42% в зависимости от периода осцилляции. Наибольшие различия наблюдаются при высоких частотах (f = 0,5–1,0 Гц), указывающие на повышенное влияние шумов и несинусоидальности сигнала. Для глицерина, как эталонной ньютоновской жидкости, расхождение составило 16,6%, что подтверждает корректность предложенной модели и ее применимость для прецизионных измерений.

Таким образом, использование интегральной формы расчета ПДВ позволяет повысить достоверность определения реологических параметров адсорбированных слоев и рекомендуется для анализа биополимерных растворов с развитыми межфазными свойствами.

Разработка интегральной формулы (11), с учетом (9), (10), (12), определения поверхностно-динамических свойств вязкости основана на фундаментальной модели комплексного дилатационного модуля, предложенной Люкассеном и ван ден Темпелем (4). Из нее следует выражение для расчета дилатационной вязкости (формулы (4)–(10)).

(4)

(5)

Относительная среднеквадратичная деформация площади поверхности, используемая в интегральном подходе к расчету дилатационной вязкости:

где 

где dt — шаг дискретизации периода или межкадровый интервал (для ССD-камеры 25 Гц dt = 0,04 с);

Δσ — амплитуда изменения ПН, мН/м.

Для сравнения результатов двух методов по ПДВ были введены условные обозначения (ηs(amp),ηs(int)) в формулах (6) и (9).

Формула (10) следует из модели комплексного дилатационного модуля, предложенной Люкассеном и ван ден Темпелем

В общем случае для вывода модифицированной формулы (11) потребовалось представить классическую модель Люкассена–ван ден Темпеля в явном виде зависимости дилатационной вязкости от амплитудных параметров колебаний (10). На этой основе была разработана интегральная форма расчета, учитывающая полную временную структуру сигнала осциллирующей капли.

Среднеквадратичное значение, среднеквадратичная деформация, RMS-деформация связана со средним значением квадрата относительной деформации следующим образом:

Величина ε (t) в течение времени равной одному периоду колебания показывает насколько площадь отклоняется от средней:

где ε (t) — относительная деформация в каждый момент времени;

εrms — относительная среднеквадратичная деформация капли, рассчитанная по всем точкам одного периода изменения.

Значения ПДВ полученные по классической формуле (6) и по формуле интегрального метода (9) с учетом (13) для глицерина имеют разницу в 16,6%: η1 = 1,8 мН·с/м, по η2 ≈1,8±0,3мН·с/м.

На основании экспериментальных данных для глицерина при частоте колебаний f=2,0 Гц и температуре 300 C проведена оценка поверхностной динамической вязкости (ηs​) при различных амплитудах модуляции: ΔА​=0,5 мм; ΔА​= 0,9 мм; ΔА​=1,0 мм. Расчеты выполнены по двум методикам: на основе классической модели (4), (5), (6) (основанное на модели Люкассена (J. Lucassen) и по предложенной интегральной модели (8), (9), (11), (13).

Установлено, что при увеличении амплитуды модуляции наблюдается рост значений ηs, указывающий на выход за пределы линейной области реологии при ΔА​=1,0 мм. В связи с этим, для верификации математической модели было выбрано значение ПДВ, полученные при более низкой амплитуде ΔА​=0.5 мм, где поведение системы ближе к стабильному и линейному, т.е. в области малых деформаций поверхностная вязкость не зависит от амплитуды возбуждения и составляет: ηs​ (ΔА​=0,5 мм)≈1,8±0,3 мН·с/м. Данное значение согласовано с литературными данными для чистого глицерина

Совпадение результатов, рассчитанных по классической формуле и по модифицированной интегральной формуле, при амплитуде 0,5 мм — это не случайность, а признак того, что система находится в линейном реологическом режиме, где обе модели эквивалентны, а измерения достоверны. Это согласуется с фундаментальными положениями межфазной реологией жидкости, изложенными в работах В.И. Ковальчука, Ж. Люкассена, Р. Миллера и соавт. 

Сравнительный анализ двух методов. Алгоритм расчета поверхностной динамической вязкости:

1. Выделить один полный период колебаний

1.1. Исходные данные:

Один период: №. 0 — 24 (25 оптических точек), Δt = 0,04 c, T = (1-4 с)

Используя формулы (6) и (9) рассчитываются ПДВ (ηs(amp),ηs(int))

2. Определить ключевые значения

2.1. Амплитуда изменения ПН:

2.2. Амплитуда изменения площади, осциллирующей капли:

2.3. Временной сдвиг Δt между минимумом A(t) и максимумом σ(t) в пределах одного периода. Расчет Δt выполняется по следующему выражению: ω=2π/T, Δϕ=ω⋅Δt,

где Δt — временное запаздывание между максимальными кривыми σ(t) и A(t) в пределах одного периода колебания.

3. Расчет ηs(amp) по классической модели (6)

4. Расчет ηs(int) по интегральной формуле (9)

4.1. Рассчитать среднее по периоду:

На практике программное обеспечение автоматически вычисляет средние значения площади поверхности и межфазного натяжения как арифметическое среднее за период колебаний, которое выводится в сводной таблице во время испытания исследуемой жидкости.

Результаты исследования показывают, что расхождение между значениями дилатационной вязкости, рассчитанными по классической модели амплитудной ηs(amp), и по интегральной формуле ηs(int)​, составляет в среднем около 41 % и сохраняется практически на одном уровне при изменении периода колебаний. Это свидетельствует о систематическом характере погрешности классического подхода, обусловленной его высокой чувствительностью к точкам максимума и минимума сигнала, особенно в условиях шумов и неидеальной формы колебаний. Интегральный метод, основанный на среднеквадратичной оценке деформации с использованием полной временной зависимости A(t), обеспечивает более устойчивые и достоверные результаты, что делает его предпочтительным для анализа реологических свойств биополимерных систем.

На графиках (рис. 1а—1г) (построенных по данным классической модели) отражающих поведение раствора ХТЗ при частотах 1 Гц, 0,5 Гц, 0,33 Гц и 0,25 Гц визуально прослеживается увеличение размаха и временного сдвига между кривыми площади поверхности и межфазного натяжения при снижении частоты.

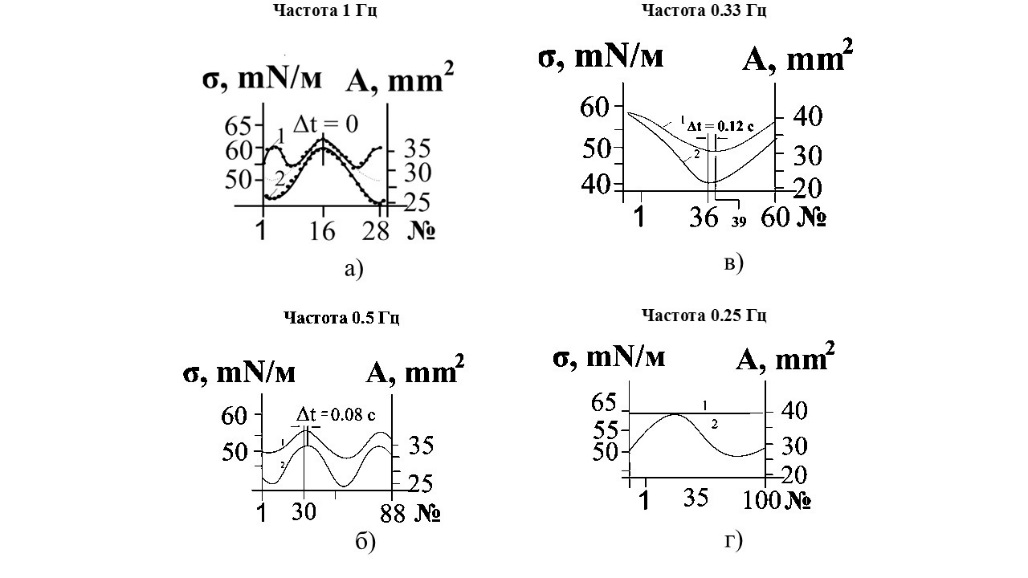
Рисунок 1 - Сравнительный анализ графиков неравновесного поверхностного натяжения и площади, осциллирующей капли при пошаговом изменении частоты с постоянной концентрацией и температуры (С = 0,5%) раствора хитозана, полученных по классической модели поверхностной динамической вязкости

Примечание: 1 — поверхностное натяжение неравновесной системы; 2 — площадь поверхности дилатирующей капли; Δt — временной сдвиг; № — номер кадра изображений CCD-камеры

DOI:10.60797/IRJ.2026.163.88.2

На рисунке 1а (T = 1 с) при частоте 1 Гц наблюдается аномальный выброс межфазного натяжения в момент подачи импульса пьезонасосом, опережающий основную фазовую кривую.

По мере уменьшения частоты колебаний (рис. 1б, T = 2 с; рис. 1в, T = 3 с) форма кривых становится стабильной, дрожание сигнала ослабевает, что указывает на переход системы в режим релаксационного равновесия. На рисунке 1в проявляется резонансоподобное поведение с максимальными значениями дилатационной вязкости, обусловленное согласованными диффузионными и адсорбционными процессами.

При дальнейшем снижении частоты до 0,25 Гц (T = 4 с) адсорбированный слой полностью релаксирует в каждом цикле (отклик на деформацию теряет периодическую зависимость). Данное явление указывает на то, что процессы перестройки слоя протекают с временной изменчивостью, не синхронной с внешним воздействием, что затрудняет определение стабильного фазового сдвига и амплитуды отклика снижении частоты до 0,25 Гц (рис. 1г, T = 4 с) периодичность межфазного натяжения теряется, что свидетельствует о полной релаксации адсорбированного слоя в каждом цикле. В этих условиях система демонстрирует свойства псевдопластичной среды.

Классический метод расчета ПДВ основан на предположении о синусоидальности сигнала и требует точного определения экстремальных значений площади поверхности капли. При наличии шумов и неидеальной формы колебаний это приводит к систематическим ошибкам в определении амплитуды относительной деформации

Классический метод расчета дилатационной вязкости раствора ХТЗ (0,5%) демонстрирует систематические погрешности до 42 % из-за чувствительности к шумам и неопределенности экстремальных точек сигнала. Предложенная интегральная формула, основанная на среднеквадратичной оценке деформации, учитывает полную временную структуру колебаний и повышает достоверность определения ПДВ. Модель развивает классическую теорию Ж. Люкассена и аналогична обработке по методу наименьших квадратов. Увеличение вязкости при снижении частоты (от 1 Гц до 0,25 Гц) указывает на формирование устойчивой межфазной структуры, характерной для псевдопластичных систем. Интегральный метод рекомендуется для анализа биополимерных жидкостей, обеспечивающий точность и воспроизводимость данных.