Application of Ritz method for calculation of stress-strain state of beams made of material with shape memory effect
Application of Ritz method for calculation of stress-strain state of beams made of material with shape memory effect
Abstract
The application of the Ritz method to the calculation of beams made of material with shape memory effect is studied. The strain energy functional is written for a TiNi nitinol material with physical nonlinearity caused by martensitic transformations in the direct transformation mode under load. The material deforms completely at a temperature above the direct martensitic transformation temperature in the austenitic state. The structural-analytical mesomechanics equations were used as the defining relations. The defining relations are written for the macro-level. Deformations of the micro and meso levels are taken into account using the orientation averaging operation of structural-analytical mesomechanics.
1. Введение
В настоящее время сплавы с эффектом памяти формы (ЭПФ) находят все большее применение в различных областях человеческой деятельности. Широкое применение они нашли в медицине, авиации, машиностроении, строительстве и др.
Сплавы с ЭПФ обладают уникальными свойствами, которые отсутствуют у большинства традиционных материалов, применяемых в промышленности. Однако, нетрадиционное поведение этих материалов требует новых моделей материала, при которых возможно применение традиционных методов механики деформированного твердого тела. Разработка теории и методов расчета инженерных конструкций, выполненных из материалов с ЭПФ, является актуальной задачей современных технологий.
2. Математическая модель
В настоящей работе используются определяющие соотношения деформационного типа, выведенные на основе общих уравнений структурно-аналитической мезомеханики
, , , . В рамках этого подхода были решены следующие краевые задачи: толстостенные трубы под внутренним давлением, стержневые статически неопределимые системы, ферменные конструкции, балки-стенки, квадратные пластины и пологие оболочки , , , . В данной работе применяется метод Ритца-Тимошенко для расчета статически неопределимых балок, выполненных из материалов с памятью формы, при произвольной нагрузке, с любыми закреплениями концов.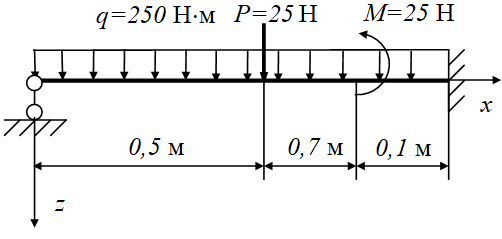
Рисунок 1 - Расчетная схема балки
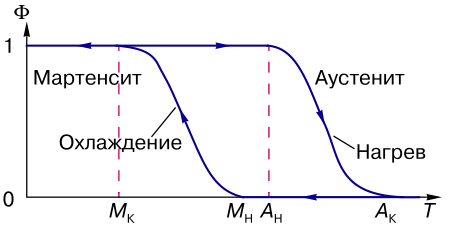
Рисунок 2 - Фазовые диаграммы для материалов с мартенситными превращениями:
МН, МK , AН, AK – характеристические температуры начала и конца превращения; Ф – объемная доля мартенсита
где σi – интенсивность напряжений; Е – модуль упругости; BФ – константа материала; ; T0 – температура термодинамического равновесия; q0 – тепловой эффект реакции; Di – дисторсия фазового превращения;
– напряжение начала прямого мартенситного превращения; TD – температура начала деформирования; MH, MK – температуры начала и конца прямого мартенситного превращения соответственно;
– напряжение конца мартенситного превращения,
; H(...) – функция Хевисайда.
Допущения, принятые при решении задачи:
1) модуль упругости материала в аустенитной и мартенситной фазах принимается одинаковым;
2) материал в условиях изотермического нагружения испытывает упругие и неупругие (фазовые) деформации;
3) для аппроксимации диаграммы деформирования принимается кубическая парабола.
По формулам модели структурно-аналитической мезомеханики
определим касательный модуль EK, максимальное напряжение σmax и фазовый предел текучести σT, определяющий начало прямого мартенситного превращения:В случае аппроксимации диаграммы материала кубической параболой (см.рис.3) определяющие соотношения примут вид :
,
,
.
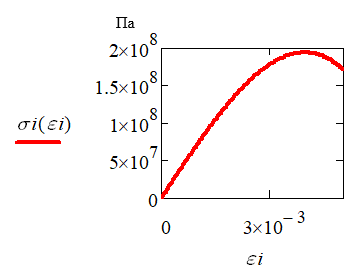
Рисунок 3 - Аппроксимация диаграммы деформирования материала TiNi кубической параболой
здесь EJy – изгибная жесткость балки, W(x)– прогиб, m – константа материала, xP, xM –координаты приложения сосредоточенной силы и момента соответственно; Jy=b⋅h3/12, Jn=b⋅h5/80; l – длина балки; b=l/7 м и h=2b – размеры поперечного сечения.
Параметры сплава TiNi, обладающего эффектом памяти формы представлены в таблице1.
3. Численная модель
Согласно методу Ритца прогиб балки в первом приближении представим в виде:
где φ(x) – аппроксимирующая функция, K – неопределенный коэффициент, представляющий собой амплитуду прогиба балки. Для построения функции φ(x) используем метод начальных параметров, что позволит учесть не только геометрические, но и силовые граничные условия. Начало координат выбираем на левом конце балки, ось х направим вправо, ось z – вниз. Согласно универсальному уравнению метода начальных параметров для балки с постоянной жесткостью, выражение для прогиба будет иметь вид:
здесь w0, φ0, M0, Q0 – начальные параметры, т.е. прогиб, угол поворота, изгибающий момент и поперечная сила в начале координат, aM=0,7 м, aP=0,5 м – координаты точки приложения момента M и силы P, соответственно.
В соответствии с рисунком 1 балка состоит из трех участков. На каждом из участков выражения для линии прогибов имеют вид:
Начальные параметры определяются исходя из граничных условий. На левой опоре имеем шарнирное закрепление w0=M0=0, на правой при x=l=0,8 м – жесткая заделка w3(l)=φ3(l)=0. Для определения φ3(l) требуется продифференцировать выражение для прогибов на третьем участке w3(x) и в полученное выражение подставить x=l. В результате для определения начальных параметров получаем следующую систему уравнений:
Решая эту систему уравнений при численных значениях коэффициентов получим: φ0=3,98/EJy, Q0=-90,4H. Найденные значения начальных параметров позволяют записать функции прогибов на каждом участке. Умножая выражения w1(x), w2(x), w3(x) на величину 24EJy/q получим окончательное выражение для аппроксимирующей функции прогиба:
Подставляя в (3) W(x)=Kφ(x), где φ(x) – функция, построенная методом начальных параметров (8), получим зависимость полной потенциальной энергии от параметра K:
где коэффициенты при параметре K определяются по формулам:
Интервал интегрирования в (9) следует разбить на три участка:
и в пределах каждого участка брать интегралы от производных соответствующих функций.
Минимизация полной потенциальной энергии балки по параметру K, приводит к нелинейному алгебраическому уравнению третьей степени относительно амплитуды прогиба K:
Решая полученное уравнение в системе Mathcad, получим K=0,0293.
4. Результаты
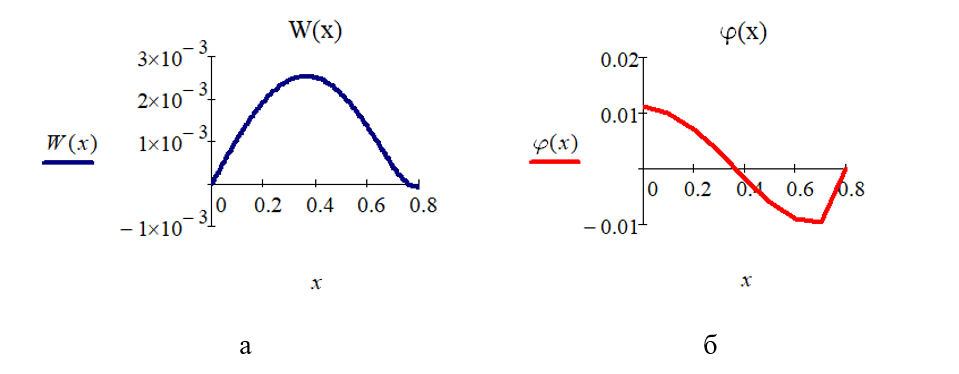
Рисунок 4 - Распределение прогиба W(x) (а) и угла поворота j(x) (б) по длине балки
Таблица 2 - Результаты расчета
Wmax×10-3, м | φmax×10-2 | Mmax×108 Нм | εmax×10-3 |
2,533 | 1,088 | 2,659 | 12,899 |
5. Заключение
В заключение можно отметить, что метод Ритца в сочетании с методом начальных параметров эффективен для расчетов балочных конструкций, выполненных из материалов с ЭПФ.
