Identification of n-link Robotic Manipulators

Авторы разработали метод, обладающий научной новизной и практической значимостью. Предложенный в данной статье подход к идентификации системы с неизвестными входами ориентирован на применение в управлении и для анализа процессов в технических устройствах

Основываясь на исследовании существующих методов идентификации

1. Гибкость: уравнение Лагранжа позволяет рассматривать различные типы систем и проводить идентификацию для каждой из них;

2. Универсальность: оно применимо для различных типов задач идентификации, включая физические системы, экономические модели и технические процессы;

3. Точность и надежность: уравнение Лагранжа основывается на строгих математических принципах и позволяет получать точные результаты идентификации;    

4. Интерпретируемость: уравнение Лагранжа позволяет получать физический смысл и интерпретировать результаты идентификации в терминах физических характеристик системы.

Несмотря на указанные преимущества у данного метода есть некоторые особенности:

1. Сложность: уравнение Лагранжа может быть сложным для решения в некоторых случаях, особенно для сложных систем с большим числом степеней свободы;

2. Ограничения на модели: уравнение Лагранжа основывается на предположении о существовании функции Лагранжа для модели системы, что может быть неверным для некоторых систем;

3. Зависимость от точности входных данных: результаты идентификации могут быть в значительной степени зависимыми от точности исходных данных и измерений, поэтому требуется аккуратная обработка данных для достижения точности и надежности.

С помощью системы уравнений Лагранжа второго рода возможно описать динамику механических систем, находящихся в геометрических связях, независимо от количества тел или точек в системе, а также от направления движения тел и типа рассматриваемого движения.

В статье решается проблема идентификации двух объектов. Первым объектом является однозвенный манипулятор с грузом, второй объект – двухзвенный манипулятор с грузом. Требуется установить, являются ли объекты идентифицируемыми на основе уравнения Лагранжа и теоремы идентифицируемости для неоднородных динамических линейных объектов.

Для вывода уравнений движений робота в обобщенных координатах используем уравнение Лагранжа второго рода

(1)

где  – кинетическая энергия системы; qi обобщенные координаты; Qi – обобщенная сила. Отметим, что уравнение (1) описывает движение механической системы, подчиненной идеальным связям.

Рассмотрим исследуемые объекты. Первый объект, представленный на рис. 1 – однозвенный манипуляционный робот, состоящий из звена длиной L0 и массой m0. Под действием внешнего управляющего момента Mu0(t) звено поворачивается на угол φ(t), который выберем в качестве обобщенной координаты. Предположим, что робот переносит деталь массой mд, величину которой будем считать неизвестной, но постоянной. При изменении угла поворота меняются силы веса F0 и Fд, которые отнесем к внешним возмущениям.

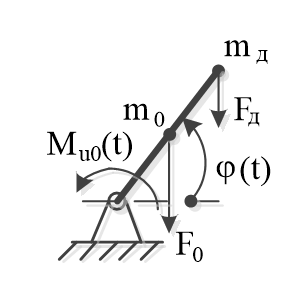
Рисунок 1 - Модель однозвенного робота

DOI:10.23670/IRJ.2024.139.166.1

Для упрощения уравнений модели звено робота будем считать тонким и абсолютно жестким стержнем, масса которого сосредоточена в его центре (центр масс). Момент инерции такого звена относительно шарнира составит J0 = m0L02/4. Наличие переносимой детали увеличит момент инерции на величину Jд = mдL02.

На звено действует вращающий момент Mu0(t) – входное управляющее воздействие, а также моменты, вызванные действием сил тяжести. Кроме того, будем считать, что в опоре создается сила вязкого трения. В результате выражение для обобщенной силы принимает вид:

где K0 – коэффициент вязкого трения, g – ускорение свободного падения,  – вращающий момент, вызванный наличием массы m0,  – вращающий момент, вызванный наличием массы mд.

Звено вращается вокруг неподвижной оси с угловой скоростью , следовательно, его кинетическая энергия будет равна

После подстановки уравнение (1) принимает вид

(2)

В результате получено нелинейное уравнение второго порядка движения однозвенного манипуляционного робота, параметры которого зависят от массы mд переносимой детали и поэтому априорно неизвестны.

Уравнение (2) можно линеаризовать. Так, если звено робота находится в положении φ0, то при малых отклонениях угла от этого положения получаем

(3)

Отметим, что в линеаризованном уравнении (3) кроме неизвестных параметров, аналогичных коэффициентам уравнения (2), появляется априорно неизвестное внешнее возмущение по входу системы

Введя обозначения

запишем уравнение (3) в матричном виде

(4)

где  – вектор состояния;  – матрица системы с параметрами  и ;  – матрица входа;  – матрица выхода.

В полученной системе уравнений (4) три неизвестных параметра. Для их вычисления требуется измерение компонент вектора состояния – угла поворота звена и величины угловой скорости. Отметим также, что ранг матрицы управляемости

т.е. линеаризованная система полностью управляемая. Ранг матрицы наблюдаемости

т.е. линеаризованная система полностью наблюдаемая. Ранг матрицы идентифицируемости зависит от значений измеряемых компонент вектора состояния, и в случае, когда начальное значение компоненты x2≠0.

т.е. система идентифицируемая. Очевидно, что в случае неподвижности звена, когда внешний управляющий момент Mu0(t) уравновешивает действие сил тяжести, система неидентифицируема.

Задаче оценки внешнего возмущающего воздействия в настоящее время уделяется огромное внимание. Для оценки внешних возмущений используют специальные наблюдатели. В частности, показано, что для полностью управляемой и наблюдаемой системы для синтеза наблюдателей возмущений можно использовать любой метод проектирования регуляторов с обратной связью

Рассмотрим второй объект, представленный на рис. 2 – двухзвенный манипуляционный робот, состоящий из первого звена длиной L0 и массой m0 и второго звена длиной L1 и массой m1. Под действием внешнего управляющего момента Mu0(t) первое звено поворачивается на угол φ0(t) и управляющего момента и Mu1(t) второго звена поворачивается на угол φ1(t). Предположим, что робот переносит деталь массой mд, величину которой будем считать неизвестной, но постоянной. При изменении угла поворота меняются силы веса F0, F1 и Fд, которые отнесем к внешним возмущениям.

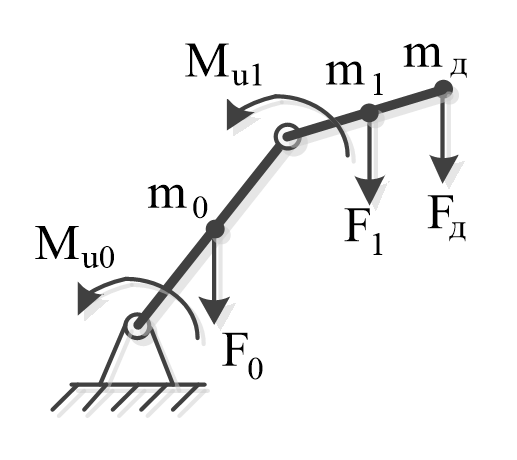
Рисунок 2 - Второй исследуемый объект

DOI:10.23670/IRJ.2024.139.166.2

Для упрощения уравнений модели звенья робота как было указано будем считать тонкими и абсолютно жесткими стержнями, масса которых сосредоточена в их центрах (центр масс). Момент инерции первого звена относительно шарнира составит J0 = m0L02/4. Наличие переносимой детали и второго звена увеличит момент инерции на величину момента инерции второго звена, которое будет определяться по сумме момента инерции детали и второго звена соответственно Jд = mдL02 и J1 = m1L12/4.

На первое звено действует вращающий момент Mu0(t) и на второе звено Mu1(t) – входное управляющее воздействие, а также моменты, вызванные действием сил тяжести. Кроме того, будем считать, что в опоре создается сила вязкого трения. В результате выражение для обобщенной силы принимает вид:

где K0 и K1 – коэффициент вязкого трения, g – ускорение свободного падения,  – вращающий момент, вызванный наличием массы m0,  – вращающий момент, вызванный наличием массы m0,  – вращающий момент, вызванный наличием массы mд.

Система состоит из двух движущихся звеньев поэтому ее кинетическая энергия:

Первое звено вращается вокруг неподвижной оси с угловой скоростью , следовательно, его кинетическая энергия будет равна

Второе звено движется поступательно вдоль оси вращения звена 1 и вращается вокруг этой оси, следовательно, его кинетическая энергия будет равна

После подстановки уравнение (1) принимает вид

(5)

В результате получили нелинейное уравнение второго порядка движения однозвенного манипуляционного робота, параметры которого звисят от массы mд переносимой детали и поэтому априорно неизвестны.

Уравнение (5) можно линеаризовать. Так, если звено робота находится в положении φ0, то при малых отклонениях угла от этого положения получаем ,

(6)

Для дальнейших расчетов введем предположение, что ; .

Отметим, что в линеаризованном уравнении (6) кроме неизвестных параметров, аналогичных коэффициентам уравнения (5), появляется априорно неизвестное внешнее возмущение по входу системы

Введем обозначения

 и ,

запишем уравнение (6) в матричном виде

(7)

где  – вектор состояния;  – матрица системы с параметрами  и ;  – матрица входа;  – матрица выхода.

В полученной системе уравнений (7) три неизвестных параметра. Для их вычисления требуется измерение компонент вектора состояния – угла поворота звена и величины угловой скорости. Отметим также, что ранг матрицы управляемости

т.е. линеаризованная система полностью управляемая. Ранг матрицы наблюдаемости

т.е. линеаризованная система полностью наблюдаемая. Ранг матрицы идентифицируемости зависит от значений измеряемых компонент вектора состояния и в случае, когда начальное значение компоненты x2≠0

т.е. система идентифицируемая. Очевидно, что в случае неподвижности звена, когда внешний управляющий момент Mu(t) уравновешивает действие сил тяжести, система неидентифицируема.

Задаче оценки внешнего возмущающего воздействия в настоящее время уделяется огромное внимание. Для оценки внешних возмущений используют специальные наблюдатели.

В частности показано, что для полностью управляемой и наблюдаемой системы для синтеза наблюдателей возмущений можно использовать любой метод проектирования регуляторов с обратной связью

Сформируем последовательность действий алгоритма идентификации манипуляционных РТС в условиях неопределенности:

1. Сформировать выражение для обобщенных сил;

2. Вычислить кинетическую энергии для одного или нескольких звеньев;

3. Получить нелинейное уравнения второго порядка движения n-звенного робота;

4. Произвести линеаризацию уравнения;

5. Осуществить переход из линейного вида в матричное представление;

6. Сделать расчет рангов матриц.

Получив положительный результат идентифицируемости исследуемых систем подтвердим его моделированием. Получим графики тестируемой модели с помощью identification toolbox, создав графики шагового воздействия и аппроксимацию. Представим результаты моделирования передаточных функции на графике (рис. 3).

А. Функция с удалением шумов;

Б. Функция с удалением выбросов.

1. Шаговое воздействие:

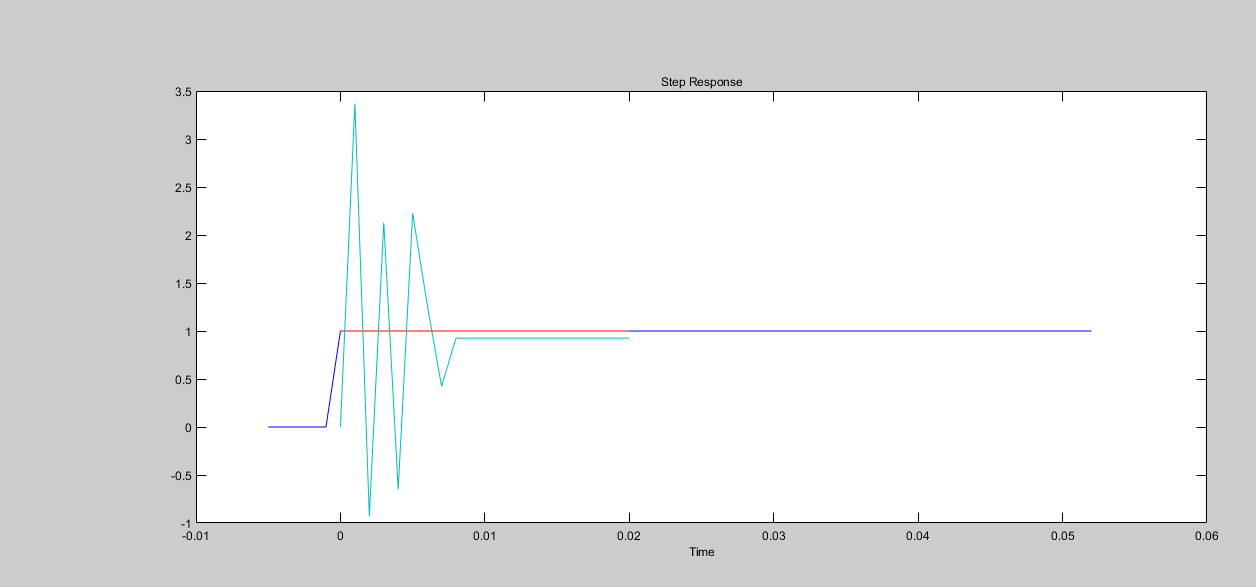
Рисунок 3 - График шагового воздействия

DOI:10.23670/IRJ.2024.139.166.3

Этот график показывает экспериментальные данные и соответствующие предсказания модели. Ось X представляет собой время, а ось Y – измеряемый отклик системы. Экспериментальные данные обозначены точками, а предсказания модели представлены линией или кривой. Кривая на графике Шагового воздействия начинается с нулевого значения и резко возрастает до установившегося значения.

График Шагового воздействия часто используется для определения важных параметров системы, таких как время установления, перерегулирование, постоянная времени, коэффициент усиления и другие параметры. Это помогает инженерам и ученым в области автоматизации и управления проектировать, анализировать и оптимизировать системы в режиме реального времени.

Без данного графика нельзя построить график разницы между экспериментальными данными и предсказаниями модели после идентификации

2. Аппроксимация модели различными передаточными функциями:

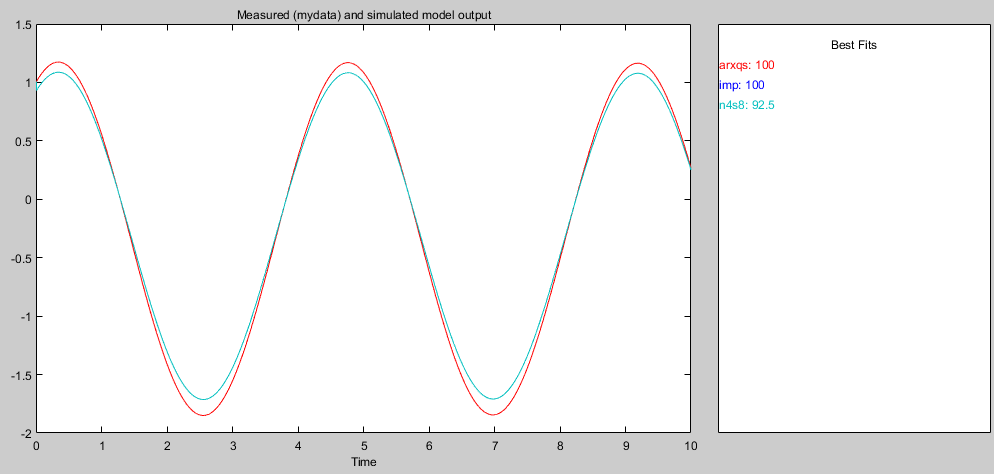
Рисунок 4 - График аппроксимации модели

DOI:10.23670/IRJ.2024.139.166.4

Этот график показывает разницу между экспериментальными данными и предсказаниями модели. Ось X обозначает время, а ось Y – абсолютное значение ошибки.

По данному графику можно увидеть неточности модели, а так же можно заметить что в максимуме и минимуме происходит пик ошибки, где происходит сильное расхождение моделей.

Произведем моделирование полученной модели идентификации:

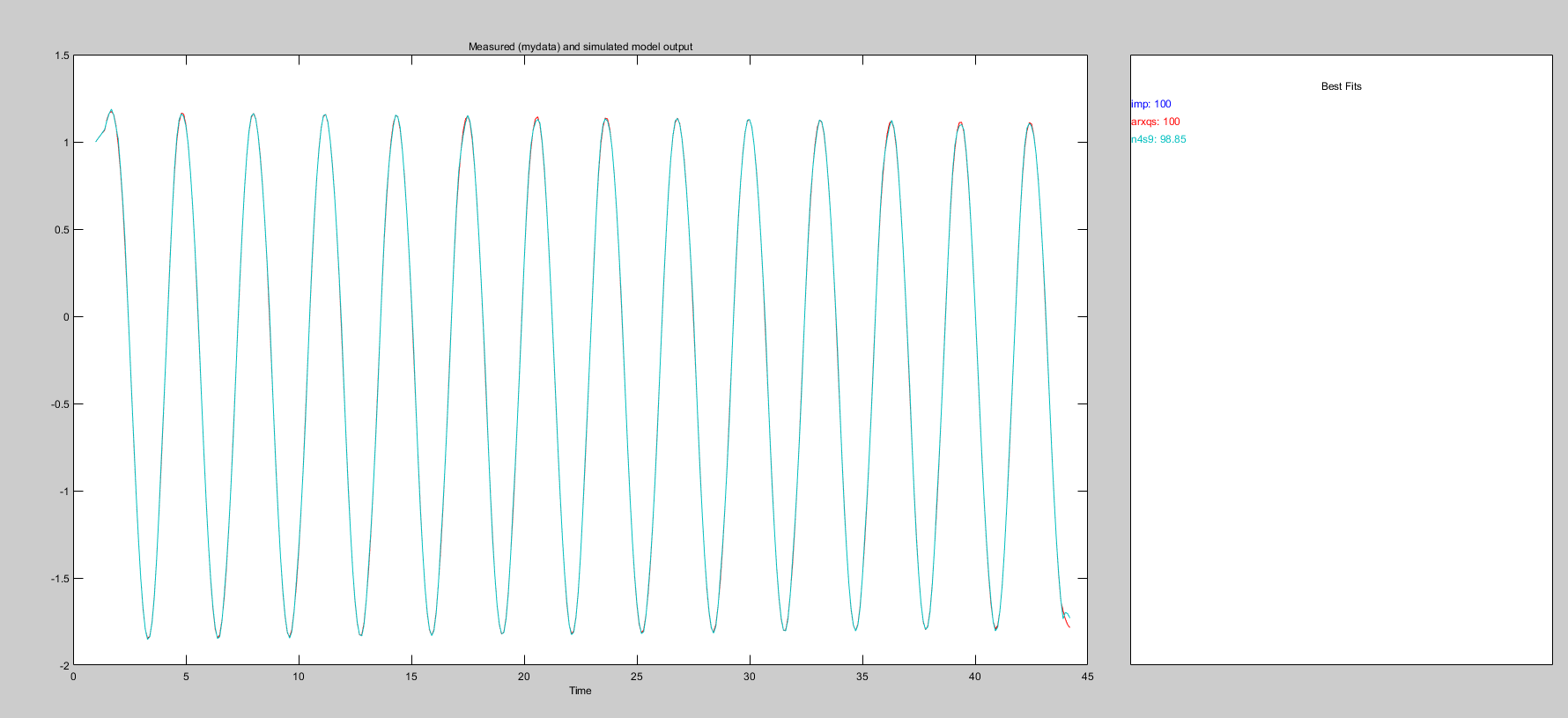
Рисунок 5 - График результатов моделирования

DOI:10.23670/IRJ.2024.139.166.5

Этот график показывает разницу между экспериментальными данными и предсказаниями модели после идентификации. Ось X обозначает время или номер эксперимента, а ось Y – остаточное значение. График остатков помогает определить наличие систематических ошибок или шума в данных и оценить адекватность модели. По графику можно выделить, что модель в целом хорошо подобрана за исключением некоторых неточностей которые можно увидеть на графике в максимуме и минимуме функции.

Среди параметров робототехнических систем (РТС)

В работе решена задача идентификации манипуляционных РТС на основе теоремы идентифицируемости для класса линейных непрерывных стационарных динамических систем на примере двухзвенного манипулятора с подвешенным грузом в условиях неопределенности параметров системы. Установлено, что объекты являются идентифицируемыми. Задача решалась поэтапно: было составлено уравнение Лагранжа, произведена линеаризация уравнения Лагранжа для адаптивной, линейной, динамической, непрерывной, стационарной системы манипуляционной РТС. Полученный алгоритм можно использовать для манипуляционных систем с двумя и более звеньями, что было подтверждено моделированием. По результатам моделирования сделан вывод, что данные системы идентифицируемы.