ПРИМЕНЕНИЕ КВАДРАТИЧНЫХ ФУНКЦИЙ ЛЯПУНОВА ПРИ РЕШЕНИИ ПРИКЛАДНЫХ ДИНАМИЧЕСКИХ ЗАДАЧ
Антоновская О.Г.
ORCID: 0000-0002-5688-7996, Кандидат физ.-мат. наук, Нижегородский государственный архитектурно-строительный университет
ПРИМЕНЕНИЕ КВАДРАТИЧНЫХ ФУНКЦИЙ ЛЯПУНОВА ПРИ РЕШЕНИИ ПРИКЛАДНЫХ ДИНАМИЧЕСКИХ ЗАДАЧ
Аннотация
В настоящей статье предлагается методика определения момента окончания переходного процесса при изменении параметров непрерывной динамической системы на основе применения прямого метода Ляпунова, основанная на оценивании областей притяжения состояний равновесия. За оценку области, которую траектория системы не покинет с течением времени, принимается окрестность состояния равновесия, в которой первая производная функции Ляпунова отрицательна. Функция Ляпунова выбирается в виде положительно определенной квадратичной формы, для которой знакоотрицательность ее первой производной в силу линеаризованной системы обеспечивается с заданным запасом.
Ключевые слова: непрерывная динамическая система, макроструктура пространства состояний, метод функций Ляпунова.
Antonovskaya O.G.
ORCID: 0000-0002-5688-7996, PhD in Physics and Mathematics, Nizhny Novgorod State University of Architecture and Civil Engineering
APPLICATION OF LYAPUNOV’S QUADRATIC FUNCTIONS IN SOLVING APPLIED DYNAMIC PROBLEMS
Abstract
In the following paper, we propose a technique for determining the moment of the end of the transient process when the parameters of a continuous dynamic system are changed on the basis of the application of the direct Lyapunov method, based on the estimation of the regions of attraction of equilibrium states. For an estimate of the region the trajectory of the system does not leave with time, we take a neighborhood of the equilibrium state where the first derivative of the Lyapunov function is negative. The Lyapunov function is chosen in the form of a positive definite quadratic form, where the negative sign of its first derivative is provided with a given margin due to a linear system.
Keywords: continuous dynamic system, macrostructure of the state space, the Lyapunov function method.
При исследовании динамики систем одной из наиболее важных является проблема определения длительности переходных процессов в системе. В ходе решения задачи определения длительности переходных процессов в существенно нелинейных системах при переключении параметров в заданном диапазоне возникает задача точного определения момента окончания переходного процесса в системе [1], [2], [3]. Дело в том, что критерием его окончания может оказаться попадание траектории на заданное, быть может, неограниченное множество, содержащее состояние равновесия, соответствующее рабочему режиму системы [1], [3]. И тот факт, что траектория попала на заданное множество, не гарантирует того, что она в дальнейшем этого множества не покинет. Таким образом, возникает задача получения оценок областей притяжения, т.е. таких областей, которые траектория с течением времени не покинет. Для решения этой задачи может быть использован второй (прямой) метод Ляпунова или метод функций Ляпунова, когда изучается поведение некоторой вспомогательной функции вдоль траекторий системы [4], [5], [6].
Центральное место во втором (прямом) методе Ляпунова занимает проблема построения функции Ляпунова. При этом функцию Ляпунова нелинейной динамической системы часто ищут в классе положительно определенных квадратичных форм, исходя из того условия, что построенная квадратичная форма является функцией Ляпунова для соответствующей линеаризованной системы [5, С. 120-132]. Кроме того, может ставиться вопрос о построении квадратичных функций Ляпунова с некоторыми заданными свойствами, которые определяются особенностями задачи. В частности, в динамических задачах, когда интерес представляют собой ухе не только качественные, но и количественные характеристики системы, возникает необходимость ограничений на первую производную функции Ляпунова вдоль траекторий системы [7,8].
В настоящей работе предлагается способ получения аналитических оценок окрестности асимптотически устойчивого состояния равновесия непрерывной динамической системы, которую траектория системы с течением времени не покинет, основанный на применении прямого метода Ляпунова и использующий методику работ [9,10].
Пусть нелинейная непрерывная динамическая система задана системой дифференциальных уравнений
![]() (1)
(1)
имеющей асимптотически устойчивое состояние равновесие ![]() . И пусть функции fi имеют непрерывные частные производные до второго порядка включительно. Запишем (1) в виде [4, C. 74-75]
. И пусть функции fi имеют непрерывные частные производные до второго порядка включительно. Запишем (1) в виде [4, C. 74-75]
![]() (2)
(2)
где 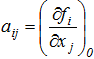 - постоянные, равные значениям частных производных функций fi при
- постоянные, равные значениям частных производных функций fi при ![]() – остаточные члены второго порядка в разложении по формуле Тейлора
– остаточные члены второго порядка в разложении по формуле Тейлора
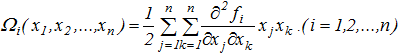 (3)
(3)
В силу непрерывности вторых производных для остаточных членов (3) на любом ограниченном множестве, содержащем состояние равновесия, можно указать оценку
![]() (4)
(4)
где 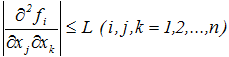
так, чтобы она была функцией Ляпунова соответствующей (2) линеаризованной системы
![]() (6)
(6)
и удовлетворяла при этом условию [6,7] ![]() , где
, где
![]() (7)
(7)
первая производная (5) в силу линеаризованной системы, а ![]() – собственные числа матрицы системы
– собственные числа матрицы системы ![]() . В [8] показано, что выбор коэффициентов (5), удовлетворяющей этому условию, можно осуществить с помощью простых явных соотношений.
. В [8] показано, что выбор коэффициентов (5), удовлетворяющей этому условию, можно осуществить с помощью простых явных соотношений.
Оценим первую производную такой функции Ляпунова для нелинейной системы (2) подобно [4].
Следует отметить, что, согласно [10], в точках поверхности уровня ![]() имеют место неравенства
имеют место неравенства
![]() (8)
(8)
где Aii – алгебраическое дополнение элемента Kii в матрице , а det K – определитель матрицы K. Но тогда, согласно (4),
![]() (9)
(9)
где ![]() есть первая производная (5) в силу уравнений линейной системы. Так как на сечении
есть первая производная (5) в силу уравнений линейной системы. Так как на сечении ![]() , то, учитывая ограничения (8), (9), получаем, что
, то, учитывая ограничения (8), (9), получаем, что
![]() (11)
(11)
первая производная в силу нелинейной системы будет отрицательной. Таким образом, доказана следующая теорема.
Теорема. Область
![]() (14)
(14)
где
![]() (15)
(15)
является оценкой снизу области притяжения асимптотически устойчивого состояния равновесия ![]() системы дифференциальных уравнений (2).
системы дифференциальных уравнений (2).
Замечание 1. Оценка (14) может быть использования при определении точного момента окончания длительности переходного процесса в динамической системе, математическая модель которой представляет собой нелинейную систему дифференциальных уравнений вида (2), при численном исследовании поведения ее траекторий. Пусть критерием окончания переходного процесса является попадание траектории системы (2) на заданное множество ![]() , содержащее устойчивое состояние равновесия системы. В случае, если множество (14)-(15)
, содержащее устойчивое состояние равновесия системы. В случае, если множество (14)-(15) ![]() , его можно принять за окрестность состояния равновесия, которую траектория системы не покинет с течение времени. Если это не так, рассмотрим множество
, его можно принять за окрестность состояния равновесия, которую траектория системы не покинет с течение времени. Если это не так, рассмотрим множество
![]() (16)
(16)
![]() (17)
(17)
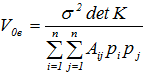 (18)
Скажем, при n=2
(18)
Скажем, при n=2
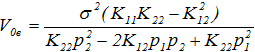 (19)
(19)
Так как в этом случае ![]() , то на множестве (16), и его можно принять за искомую окрестность состояния равновесия. То есть в качестве окрестности состояния равновесии (2), которую траектория системы не покинет с течением времени, можно взять множество
, то на множестве (16), и его можно принять за искомую окрестность состояния равновесия. То есть в качестве окрестности состояния равновесии (2), которую траектория системы не покинет с течением времени, можно взять множество
![]() (20)
(20)
где ![]() , а момент окончания переходного процесса в системе определять следующим образом.
, а момент окончания переходного процесса в системе определять следующим образом.
За начальную точку траектории выберем точку, координаты которой соответствуют координатам состояния равновесия при значении параметра, с которого происходит переключение, по отношению к координатам состояния равновесия ![]() , соответствующего значению параметра, на которое переключение происходит. Вычисления будем проводить до тех пор, пока траектория системы не попадет на множество
, соответствующего значению параметра, на которое переключение происходит. Вычисления будем проводить до тех пор, пока траектория системы не попадет на множество ![]() , содержащее
, содержащее ![]() . Запомнив момент попадания траектории на
. Запомнив момент попадания траектории на ![]() , продолжим вычисления до тех пор, пока либо траектория не попадет в область (19), либо не покинет множество
, продолжим вычисления до тех пор, пока либо траектория не попадет в область (19), либо не покинет множество ![]() . В первом случае будем считать моментом окончания переходного процесса запомненный ранее момент попадания в
. В первом случае будем считать моментом окончания переходного процесса запомненный ранее момент попадания в ![]() , во втором – продолжим вычисления до следующего момента попадания траектории на
, во втором – продолжим вычисления до следующего момента попадания траектории на ![]() , с последующим повторением всей процедуры.
, с последующим повторением всей процедуры.
Замечание 2. Доказанная теорема может быть использована для получения оценок области притяжения состояния равновесия нелинейной системы (2) [9]. Пусть мы ищем оценку области притяжения состояния равновесия ![]() системы (2), принадлежащую ограниченному множеству
системы (2), принадлежащую ограниченному множеству ![]() . Поскольку поверхности уровня
. Поскольку поверхности уровня ![]() , вписанной в
, вписанной в ![]() , соответствует значение
, соответствует значение ![]() [9], то искомой аналитической оценкой области притяжения является множество
[9], то искомой аналитической оценкой области притяжения является множество
![]() (21)
(21)
Замечание 3. 1. Пусть все корни характеристического уравнения, соответствующего состоянию равновесия ![]() , действительны и различны, причем
, действительны и различны, причем ![]() . В этом случае всегда существует линейное невырожденное преобразование координат, приводящее систему (10) к каноническому виду (столбцы матрицы преобразования координат являются собственными векторами матрицы A, соответствующими собственным значениям
. В этом случае всегда существует линейное невырожденное преобразование координат, приводящее систему (10) к каноническому виду (столбцы матрицы преобразования координат являются собственными векторами матрицы A, соответствующими собственным значениям ![]() соответственно).
соответственно).
Рассмотрим систему дифференциальных уравнений вида
![]() (22)
(22)
Следует отметить, что согласно [8], квадратичную функцию Ляпунова для системы (22) можно выбрать в виде
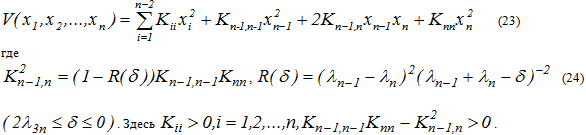 Тогда, в силу доказанной теоремы, получим, что в этом случае
Тогда, в силу доказанной теоремы, получим, что в этом случае
- Пусть все корни характеристического уравнения, соответствующего состоянию равновесия
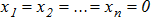 , таковы, что
, таковы, что 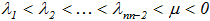 , т.е. действительны и различны. И пусть
, т.е. действительны и различны. И пусть 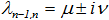 . В этом случае всегда существует линейное невырожденное преобразование координат, приводящее линеаризованную систему к каноническому виду [4].
. В этом случае всегда существует линейное невырожденное преобразование координат, приводящее линеаризованную систему к каноническому виду [4].
Рассмотрим систему дифференциальных уравнений
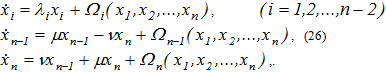
Заметим [7], что в этом случае квадратичную функцию Ляпунова, удовлетворяющую условию ![]() , можно выбрать в виде (23), где
, можно выбрать в виде (23), где
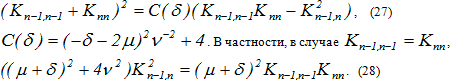
Список литературы / References
- Горюнов В. И. Техническая полоса захвата одноконтурного синтезатора частоты / В. И. Горюнов, В. Н. Ерусланов, Н. И. Лобашов // Техника средств связи. Сер. Техника радиосвязи. – 1990. – Вып. 2. – С. 88-94.
- Горюнов В. И. К анализу быстродействия синтезатора при переключениях по диапазону / В. И. Горюнов, В. Н. Ерусланов, М. Н. Зайцева // Техника средств связи. Сер. Техника радиосвязи. – 1986. – Вып. 3. – С. 44-49.
- Антоновская О. Г. К анализу формы и длительности переходных процессов при переключениях синтезатора с делителем частоты и пропорционально-интегрирующим фильтром по диапазону / О. Г. Антоновская, В. И. Горюнов, Н. И. Лобашов // Динамика систем: Межвуз. сб. Горький: Изд-во ГГУ, 1989. – С.59-72.
- Ляпунов А. М. Общая задача об устойчивости движения. / А. М. Ляпунов.. – М.-Л.: Изд-во техн.-теор. лит., 1950. – 472 с.
- Барбашин Е. А. Функции Ляпунова. / Е. А. Барбашин. – М. Наука, 1970. – 240 с.
- Четаев Н. Г. Устойчивость движения. / Н. Г. Четаев. – М.: Наука, 1965. – 207 с.
- Антоновская О. Г. О построении квадратичной функции Ляпунова с заданными свойствами / О. Г. Антоновская // Дифференциальные уравнения. – 2013. – Т.49. – № 9. – С. 1220-1224.
- Антоновская О. Г. О построении квадратичной функции Ляпунова с заданными свойствами / О. Г. Антоновская // Дифференциальные уравнения. – 2016. – Т.52. – № 3. – С. 276-281.
- Антоновская О. Г. Об одном способе оценки области притяжения устойчивого решения системы дифференциальных уравнений / О. Г. Антоновская // Международный научный журнал «Инновационная наука». – 2015. – №9. – С. 11-15.
- Антоновская О. Г. Об одном способе оценки размеров области притяжения неподвижной точки нелинейного точечного отображения произвольной размерности / О. Г. Антоновская, В. И. Горюнов // Известия вузов. Математика. – 2016. – № 12. – С. 12-18.
Список литературы на английском языке / References in English
- Goryunov V. I. Tehnicheskaya polosa zahvata odnokonturnogo sintezatora chastoty [Technical capture strip of one-contour frequency synthesizer] / V .I. Goryunov, V. N. Eruslanov, N. I. Lobashov // Tehnika sredstv svyasi. Ser. Tehnika radiosvyasi [Techniques of communication. Series Techniques of radio-communication]. – 1990. Vyp. 2. P. 88–94. [in Russian]
- Goryunov V.I. K analizu bystrodeystviya sintezatora pri pereklucheniyah po diapazonu [On synthesizer speed analysis when switching in a range] / V .I. Goryunov, V. N. Eruslanov, M. N. Zaytseva // Tehnika sredstv svyasi. Ser. Tehnika radiosvyasi [Techniques of communication. Series Techniques of radio-communication]. – 1986. Vyp. 3. P. 44–49. [in Russian]
- Antonovskaya O. G. K analizu formy I dlitelnosti perehodnyh processov pri pereklyucheniyah sintezatora s delitelem chastity I proportsionalno-integrtiruyushim filtrom po diapazonu [On the analysis of form and duration of transient processes when switching over a range in the synthesizer with counter and proportional-integrating filter] / O. G. Antonovskaya, V. I. Goryunov, N. I. Lobashov // Dinamika system: Mezhvuz. sbornik [System dynamics: Inter-university Collection]. – Gorky: Izd-vo GGU, 1989. P. 59–72. [in Russian]
- Lyapunov A. M. Obshchaya zadacha ob ustoychivosti dvizheniya [General problem of the stability of motion]. / A. M. Lyapunov. – Moscow–Leningrad : Izdat. Nthn.-teor. Lit., 1950. 472 p.
- Barbashin E.A. Funktsii Lyapunova [Lyapunov functions]. /E. A. Barbashin. – Moscow: Nauka, 1970. 240 p.
- Chataev N. G. Ustoychivost’ dvizheniya [Stability of motion]. / N. G. Chetaev. – Moscow: Nauka, 1966. 207 p.
- Antonovskaya O. G. On the construction of quadratic Lyapunov function with given properties / O. G. Antonovskaya // Differential equations. – 2013. – V. 49. – № 9. – P. 1187-1191.
- Antonovskaya O. G. Determination of coefficients of a quadratic Lyapunov function with given properties / O. G. Antonovskaya // Differential equations. – 2016. – V. 52. – № 3. – P. 275-261.
- Antonovskaya O. G. Ob odnom sposobe otsenki oblasti prityazheniya ustoychivogo resheniya sistemy differentsialnyh uravneniy [On a method of evaluation of attraction domain for fixed point of the stable solution of differential system] / O. G. Antonovskaya // Mezhdunarodnyy zhurnal ”Innovatsionnaya nauka” [International magazine ”Innovation Science”].– 2015. – № 9. – P. 11-15. [in Russian]
- Antonovskaya O. G. On a method of evaluation of attraction domain for fixed point of nonlinear point mapping of arbitrary dimension / O. G. Antonovskaya, V. I. Goryunov // Russian Mathematics.– 2016. – V. 60. – № 12. – P. 10-14.
