ПОСТРОЕНИЕ УСЛОВНО-ЭКСТРЕМАЛЬНЫХ ФУНКЦИЙ ЛЯПУНОВА ПРИ ИЗУЧЕНИИ ПОВЕДЕНИЯ ТРАЕКТОРИЙ НЕПРЕРЫВНЫХ ДИНАМИЧЕСКИХ СИСТЕМ НА ПЛОСКОСТИ
Антоновская О.Г.1, Зайцева М.Н.2
1ORCID: 0000-0002-5688-7996, Кандидат физ.-мат. наук, Нижегородский государственный архитектурно-строительный университет, 2ORCID: 0000-0002-3649-0385, Нижегородский государственный автомеханический техникум
ПОСТРОЕНИЕ УСЛОВНО-ЭКСТРЕМАЛЬНЫХ ФУНКЦИЙ ЛЯПУНОВА ПРИ ИЗУЧЕНИИ ПОВЕДЕНИЯ ТРАЕКТОРИЙ НЕПРЕРЫВНЫХ ДИНАМИЧЕСКИХ СИСТЕМ НА ПЛОСКОСТИ
Аннотация
В работе решается задача построения условно-экстремальной функции Ляпунова для непрерывной динамической системы, описываемой системой дифференциальных уравнений второго порядка. Это квадратичной функции Ляпунова, гарантирующая минимальность времени до попадания траектории линеаризованной в окрестности состояния равновесия системы, в сечение функции Ляпунова, вписанное в заданную полосу. В отношении квадратичной функции Ляпунова предполагается выполнение условия равенства отношения минимума модуля первой производной функции Ляпунова на сечении к значению самой функции заданному числу. Условно-экстремальная функции Ляпунова ищется как квадратичная функция Ляпунова рассматриваемого класса, на сечение которой, вписанное в полосу, попадает траектория линеаризованной в окрестности состояния равновесия системы с заданной начальной точкой.
Ключевые слова: непрерывная динамическая система, система дифференциальных уравнений, квадратичная функция Ляпунова.Antonovskaya O.G.1, Zaytseva M.N.2
1ORCID: 0000-0002-5688-7996, PhD in Physics and Mathematics, Nizhny Novgorod State University of Architecture and Civil Engineering, 2ORCID: 0000-0002-3649-0385, Nizhny Novgorod State Automotive Technical School
CONSTRUCTION OF THE CONDITION-EXTREMAL LYAPUNOV FUNCTIONS IN STUDIES OF THE TRAJECTORIES BEHAVIOR OF CONTINUOUS DYNAMIC SYSTEMS ON A PLANE
Abstract
The paper presents the solution of the problem of constructing a conditionally extremal Lyapunov function for a continuous dynamical system described by a system of second-order differential equations. This is a quadratic Lyapunov function, which guarantees the minimality of the time before the linearization of a trajectory in a neighborhood of the equilibrium state of the system, into the section of the Lyapunov function inscribed in a given band. With respect to the quadratic Lyapunov function, it is assumed that the condition of equality of the ratio of the modulus minimum of the first derivative of the Lyapunov function on the section to the value of the function itself to a given number is fulfilled. A conditional-extremal Lyapunov function is sought as a quadratic Lyapunov function of the class under consideration, the cross-section of which, inscribed in the strip, is the trajectory of a system linearized in a neighborhood of the equilibrium state with a given initial point.
Keywords: continuous dynamical system, system of differential equations, quadratic Lyapunov function.
- Введение
При исследовании динамики систем одной из наиболее важных является проблема определения длительности переходных процессов в системе. Причем критерием окончания переходного процесса в системе может оказаться попадание траектории на заданное, быть может, неограниченное множество, содержащее состояние равновесия, соответствующее рабочему режиму системы [1-3]. И тот факт, что траектория попала на заданное множество, не гарантирует того, что она в дальнейшем этого множества не покинет. Таким образом, возникает задача оценивания подобластей притяжения, гарантирующих окончания переходного процесса с заданной точностью. Для решения этой задачи может быть использован второй (прямой) метод Ляпунова или метод функций Ляпунова [4-6], когда изучается поведение некоторой вспомогательной функции вдоль траекторий системы. При этом функцию Ляпунова нелинейной динамической системы часто ищут [5, C. 120-132] в классе положительно определенных квадратичных форм, исходя из того условия, что построенная квадратичная форма является функцией Ляпунова для соответствующей линеаризованной системы. Кроме того, может ставиться вопрос о построении квадратичных функций Ляпунова с некоторыми заданными свойствами, которые определяются особенностями задачи [7-9].
В настоящей работе решается задача построения квадратичной функции Ляпунова, гарантирующей минимальность времени до попадания траектории линеаризованной системы второго порядка в сечение функции Ляпунова, вписанное в полосу, при условии равенства отношения минимума модуля первой производной функции Ляпунова на сечении к значению самой функции заданному числу. Такая функция Ляпунова была названа условно-экстремальной [10].
- Постановка задачи
Пусть нелинейная непрерывная динамическая система задана системой дифференциальных уравнений
![]() (1)
(1)
имеющей асимптотически устойчивое состояние равновесие ![]() . И пусть функции fi имеют непрерывные частные производные до второго порядка включительно. Тогда система (1) допускает линеаризацию в окрестности состояния равновесия [4, C. 74-75]. И пусть соответствующая ей линеаризованная система имеет вид
. И пусть функции fi имеют непрерывные частные производные до второго порядка включительно. Тогда система (1) допускает линеаризацию в окрестности состояния равновесия [4, C. 74-75]. И пусть соответствующая ей линеаризованная система имеет вид
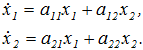 (2)
(2)
Зададим начальную точку ![]() . Известно [4, С. 71], что поведение траекторий системы (2) в окрестности состояния равновесия
. Известно [4, С. 71], что поведение траекторий системы (2) в окрестности состояния равновесия ![]() определяется видом корней характеристического уравнения
определяется видом корней характеристического уравнения
![]() (3)
(3)
В дальнейшем будем предполагать, что корни (3) простые и, кроме того, ![]() , т.е. состояние равновесия
, т.е. состояние равновесия ![]() асимптотически устойчиво.
асимптотически устойчиво.
Пусть также задана полоса
![]() (4)
(4)
Для определения момента окончания переходного процесса в системе необходим критерий, гарантирующий не только попадание в полосу (4) траектории линеаризованной системы (2) с начальной точкой , но и тот факт, что в дальнейшем траектория этой полосы не покинет. Для его получения воспользуемся методом функций Ляпунова. Рассмотрим множество квадратичных функций Ляпунова
![]() (5)
(5)
построенных для системы (2). Задача состоит в нахождении параметров квадратичной функции Ляпунова класса (5), удовлетворяющей условию ![]() и гарантирующей минимальность времени до попадания траектории линеаризованной системы (2) в сечение функции Ляпунова, вписанное в полосу (4) (т.е. условно-экстремальной функции Ляпунова).
и гарантирующей минимальность времени до попадания траектории линеаризованной системы (2) в сечение функции Ляпунова, вписанное в полосу (4) (т.е. условно-экстремальной функции Ляпунова).
- Методика построения условно-экстремальной функции Ляпунова
1. В случае, когда ![]() вещественные,
вещественные, ![]() , система (2) линейным невырожденным преобразованием координат
, система (2) линейным невырожденным преобразованием координат
![]() (6)
(6)
![]() (7)
(7)
на плоскости ξ,η, функция ![]() (5) преобразуется как
(5) преобразуется как ![]() , где есть положительно определенная квадратичная форма
, где есть положительно определенная квадратичная форма
![]() (10)
(10)
а сечение функции Ляпунова (5) ![]() , вписанное в полосу (4), переходит в сечение функции (10)
, вписанное в полосу (4), переходит в сечение функции (10) ![]() , вписанное в полосу (9), причем
, вписанное в полосу (9), причем
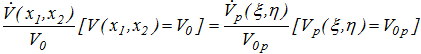 (12)
(12)
где ![]() – первая производная (4) в силу (2), а
– первая производная (4) в силу (2), а ![]() – первая производная (10) в силу (8). Условие (11) гарантирует тот факт, что (10) есть функция Ляпунова для канонической системы (8).
– первая производная (10) в силу (8). Условие (11) гарантирует тот факт, что (10) есть функция Ляпунова для канонической системы (8).
Согласно [7,8] функция ![]() удовлетворяет условию
удовлетворяет условию ![]() , если
, если
![]() (13)
(13)
Будем искать сечение ![]() , вписанное в полосу (9), такое, что траектория (8) с начальной точкой (координаты которой ищутся по
, вписанное в полосу (9), такое, что траектория (8) с начальной точкой (координаты которой ищутся по ![]() в силу (6)) не принадлежащей полосе, попадет в него за минимальное время tmin. А поскольку для сечения
в силу (6)) не принадлежащей полосе, попадет в него за минимальное время tmin. А поскольку для сечения ![]() квадратичной функции (10), вписанного в полосу
квадратичной функции (10), вписанного в полосу ![]() , то математическая постановка задачи суть
, то математическая постановка задачи суть
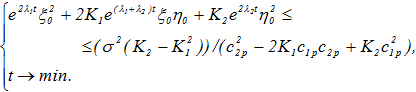 (14)
(14)
Причем если через точку пересечения траектории с границей полосы проходит вписанное в полосу сечение функции Ляпунова рассматриваемого класса, то соответствующая функция Ляпунова является условно-экстремальной. Для точек (ξ,η) прямой ![]() подобная ситуация имеет место только, если
подобная ситуация имеет место только, если
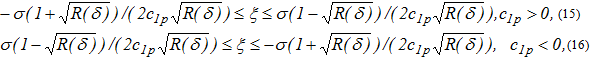
ξ – любое при ![]() (η ищется из уравнения
(η ищется из уравнения ![]() ), для точек прямой
), для точек прямой ![]()
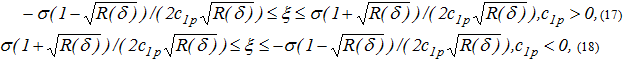
ξ – любое при ![]() (η ищется из уравнения
(η ищется из уравнения ![]() ). Соответствующие значения
). Соответствующие значения ![]() могут быть найдены по формулам
могут быть найдены по формулам
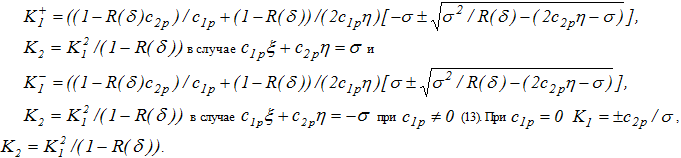
Если сечения рассматриваемого класса, проходящего через точку пересечения траектории с границей полосы не существует, то движение вдоль траектории продолжается до момента попадания на огибающую семейства сечений функций Ляпунова (10),(13), вписанных в полосу, а именно на одну из кривых
![]() (19)
(19)
и ![]() . Соответствующие значения K2 можно легко найти в силу (13).
. Соответствующие значения K2 можно легко найти в силу (13).
На рис. 1 показано, как располагается огибающая семейства эллипсов при различных допустимых значениях δ. При этом, в случае ![]() , кривые (19), (20) вырождаются в прямые
, кривые (19), (20) вырождаются в прямые ![]() , а в случае δ = 0 область, ограниченная прямыми и огибающей, дает максимально возможную для класса квадратичных функций Ляпунова оценку области притяжения устойчивого состояния равновесия, целиком принадлежащую полосе. Для кривых, изображенных на рис.1,
, а в случае δ = 0 область, ограниченная прямыми и огибающей, дает максимально возможную для класса квадратичных функций Ляпунова оценку области притяжения устойчивого состояния равновесия, целиком принадлежащую полосе. Для кривых, изображенных на рис.1, ![]() .
.
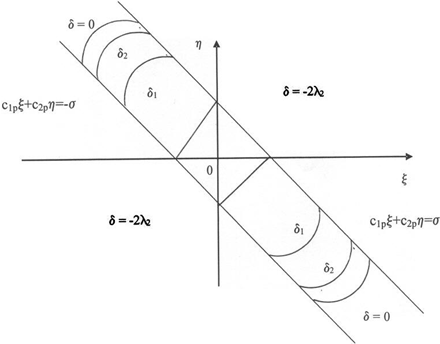
Рис. 1 – Расположение огибающей семейства эллипсов при допустимых значениях δ в случае действительных значений ![]()
Таким образом, для построения условно-экстремальной функции Ляпунова для исходной нелинейной системы (1) можно поступить следующим образом. Поскольку ![]() при
при ![]() , уравнение
, уравнение ![]() имеет конечное число корней. Пусть
имеет конечное число корней. Пусть ![]() – наибольший из них. Рассмотрим точку
– наибольший из них. Рассмотрим точку ![]() пересечения траектории с границей полосы. Если эта точка принадлежит одному из множеств (15)-(18), то условно-экстремальной будет являться функция, коэффициенты которой ищутся из формулы
пересечения траектории с границей полосы. Если эта точка принадлежит одному из множеств (15)-(18), то условно-экстремальной будет являться функция, коэффициенты которой ищутся из формулы
![]() (21)
(21)
при учете (13). Если же эта точка не принадлежит ни одному из рассмотренных множеств, то ищется точка пересечения траектории системы с одной из кривых (19), (20), и строится функция Ляпунова с коэффициентами, соответствующими точкам этих кривых.
- В случае, когда
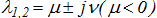 , система (2) линейным невырожденным преобразованием координат [4, С. 74-75]
, система (2) линейным невырожденным преобразованием координат [4, С. 74-75]
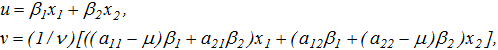 (22)
где
(22)
где При этом функция ![]() (6) преобразуется как
(6) преобразуется как ![]() , где
, где ![]() - положительно определенная квадратичная форма
- положительно определенная квадратичная форма
![]() (24)
(24)
на плоскости u,v, а сечение функции Ляпунова (4) ![]() , вписанное в полосу (4), перейдет в сечение функции (24)
, вписанное в полосу (4), перейдет в сечение функции (24) ![]() , вписанное в полосу (25), причем
, вписанное в полосу (25), причем
![]() (26)
(26)
Подобно предыдущему случаю можно показать [7], что ![]() является функцией Ляпунова, если имеет место
является функцией Ляпунова, если имеет место
![]() (27)
(27)
Более того, условие ![]() имеет место на любом сечении
имеет место на любом сечении ![]() , если
, если
![]() (28)
(28)
Принимая во внимание (28)-(29), а также тот факт, что для любого сечения ![]() , вписанного в полосу,
, вписанного в полосу,
![]() (30)
(30)
получаем следующую математическую постановку задачи нахождения условно-экстремальной функции Ляпунова для траектории с заданной начальной точкой ![]()
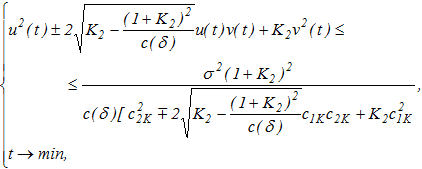 (31)
(31)
где ![]() .
.
Для точек прямой ![]() сечение квадратичной функции Ляпунова, удовлетворяющее условию
сечение квадратичной функции Ляпунова, удовлетворяющее условию ![]() и вписанное в полосу, существует только, если
и вписанное в полосу, существует только, если
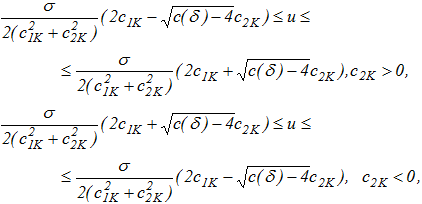 (32)
(32)
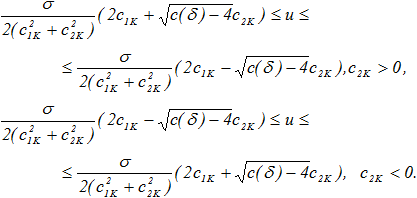 (33)
(33)
Если сечения рассматриваемого класса, проходящего через точку пересечения траектории отображения с границей полосы не существует, то движение вдоль траектории продолжается до момента попадания на огибающую семейства сечений функций Ляпунова (27), вписанных в полосу, а именно на одну из кривых
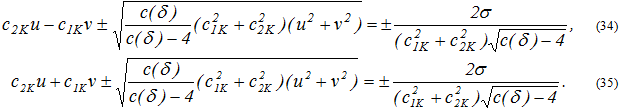
Легко проверить, что отрезки прямых (32),(33) и куски кривых (34),(35) стыкуются в точках прямых ![]() . На рис. 2 приведен вид огибающей для
. На рис. 2 приведен вид огибающей для ![]() = 1, μ=-1,ν = , δ = 0, 0.5, 2.
= 1, μ=-1,ν = , δ = 0, 0.5, 2.
Заметим, что область, ограниченная прямыми и огибающей семейства сечений в случае δ = 0 дает максимально возможную для класса квадратичных функций Ляпунова оценку множества, принадлежащего полосе и обладающего тем свойством, что траектория системы (23) не сможет его покинуть с течением времени. Случай δ = ![]() в данном случае является особым. В этом случае c(δ) = 4 и существует единственное значение K2=1, для которого сечение
в данном случае является особым. В этом случае c(δ) = 4 и существует единственное значение K2=1, для которого сечение ![]() вписано в полосу.
вписано в полосу.
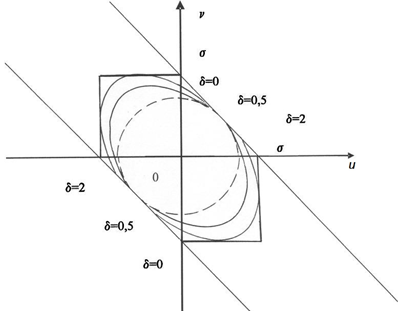
Рис. 2 – Расположение огибающей семейства эллипсов при допустимых значениях δ в случае комплексных значений ![]()
Непосредственно о построении условно-экстремальной функции Ляпунова для траектории нелинейной системы, соответствующей (23), с начальной точкой ![]() (координаты которой ищутся по
(координаты которой ищутся по ![]() в силу (22)), можно отметить следующее. Воспользуемся тем, решение системы (23) с начальной точкой
в силу (22)), можно отметить следующее. Воспользуемся тем, решение системы (23) с начальной точкой ![]() может быть записано как
может быть записано как
где ![]() . Легко видеть, что точки пересечения (36) с одной из границ полосы, а также соответствующие значения t>0 могут быть найдены из уравнений
. Легко видеть, что точки пересечения (36) с одной из границ полосы, а также соответствующие значения t>0 могут быть найдены из уравнений
![]() (37)
(37)
Т.к. ![]() , то существует конечное число решений (37), причем интерес представляет t0, являющееся максимальным из них.
, то существует конечное число решений (37), причем интерес представляет t0, являющееся максимальным из них.
Если значение t0 таково, что u(t0) принадлежит одному из отрезков (32),(33) прямых ![]() , то соответствующие значения K2 легко можно найти из соотношений
, то соответствующие значения K2 легко можно найти из соотношений
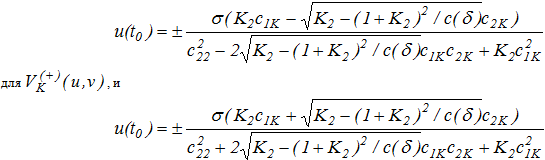
Если значение t0 таково, что u(t0) не принадлежит ни одному из отрезков (32),(33), то ищется точка пересечения траектории (36) с любой из кривых (34),(35) в полосе. Поскольку попадание траектории внутрь области, ограниченной огибающей и отрезками (32),(33) прямых ![]() гарантирует ее невыход из этой области, то существует единственное значение
гарантирует ее невыход из этой области, то существует единственное значение ![]() , отвечающее решению задачи.
, отвечающее решению задачи.
- Заключение
Приведенные выше рассуждения показывают, что, как и в случае дискретных динамических систем [10], в случае непрерывных динамических систем на плоскости задача построения условно-экстремальной функции Ляпунова допускает аналитическое решение. Причем построенная таким образом квадратичная функция Ляпунова удобна для применения в задаче нахождения длительности переходных процессов в системе.
Список литературы / References
- Горюнов В. И. Техническая полоса захвата одноконтурного синтезатора частоты / В. И. Горюнов, В. Н. Ерусланов, Н. И. Лобашов // Техника средств связи. Сер. Техника радиосвязи. – 1990. – Вып. 2. – С. 88-94.
- Горюнов В. И. К анализу быстродействия синтезатора при переключениях по диапазону / В. И. Горюнов, В. Н. Ерусланов, М. Н. Зайцева // Техника средств связи. Сер. Техника радиосвязи. – 1986. – Вып. 3. – С. 44-49.
- Антоновская О. Г. К анализу формы и длительности переходных процессов при переключениях синтезатора с делителем частоты и пропорционально-интегрирующим фильтром по диапазону / О. Г. Антоновская, В. И. Горюнов, Н. И. Лобашов // Динамика систем: Межвуз. сб. Горький: Изд-во ГГУ, 1989. – С.59-72.
- Ляпунов А. М. Общая задача об устойчивости движения. / А. М. Ляпунов.. – М.-Л.: Изд-во техн.-теор. лит., 1950. – 472 с.
- Барбашин Е. А. Функции Ляпунова. / Е. А. Барбашин. – М. Наука, 1970. – 240 с.
- Четаев Н. Г. Устойчивость движения. / Н. Г. Четаев. – М.: Наука, 1965. – 207 с.
- Антоновская О. Г. О построении квадратичной функции Ляпунова с заданными свойствами / О. Г. Антоновская // Дифференциальные уравнения. – 2013. – Т.49. – № 9. – С. 1220-1224.
- Антоновская О. Г. Об определении коэффициентов квадратичной функции Ляпунова с заданными свойствами / О. Г. Антоновская // Дифференциальные уравнения. – 2016. – Т.52. – № 3. – С. 276-281.
- Сарыбеков Р.А. Экстремальные квадратичные функции Ляпунова систем уравнений второго порядка. / Р.А. Сарыбеков // Сиб. матем. хурн. – 1977. – Т. 18. – № 5. – С. 1159-1167.
- Антоновская О. Г. О построении и применении условно-экстремальной функции Ляпунова при изучении динамики системы с помощью точечного отображения плоскости в плоскость / О. Г. Антоновская, В. И. Горюнов // Математическое моделирование и оптимальное управление. Вестник ННГУ. Н. Новгород: Изд-во ННГУ. – 2006. – №3(32). – С. 110-117.
Список литературы на английском языке / References in English
- Goryunov V. I. Tehnicheskaya polosa zahvata odnokonturnogo sintezatora chastoty [Technical capture strip of one-contour frequency synthesizer] / V .I. Goryunov, V. N. Eruslanov, N. I. Lobashov // Tehnika sredstv svyasi. Ser. Tehnika radiosvyasi [Techniques of communication. Series Techniques of radio-communication]. – 1990. Vyp. 2. P. 88–94. [in Russian]
- Goryunov V.I. K analizu bystrodeystviya sintezatora pri pereklucheniyah po diapazonu [On synthesizer speed analysis when switching in a range] / V .I. Goryunov, V. N. Eruslanov, M. N. Zaytseva // Tehnika sredstv svyasi. Ser. Tehnika radiosvyasi [Techniques of communication. Series Techniques of radio-communication]. – 1986. Vyp. 3. P. 44–49. [in Russian]
- Antonovskaya O. G. K analizu formy I dlitelnosti perehodnyh processov pri pereklyucheniyah sintezatora s delitelem chastity I proportsionalno-integrtiruyushim filtrom po diapazonu [On the analysis of form and duration of transient processes when switching over a range in the synthesizer with counter and proportional-integrating filter] / O. G. Antonovskaya, V. I. Goryunov, N. I. Lobashov // Dinamika system: Mezhvuz. sbornik [System dynamics: Inter-university Collection]. – Gorky: Izd-vo GGU, 1989. P. 59–72. [in Russian]
- Lyapunov A. M. Obshchaya zadacha ob ustoychivosti dvizheniya [General problem of the stability of motion]. / A. M. Lyapunov. – Moscow–Leningrad : Izdat. Nthn.-teor. Lit., 1950. 472 p. [in Russian]
- Barbashin E.A. Funktsii Lyapunova [Lyapunov functions]. /E. A. Barbashin. – Moscow: Nauka, 1970. 240 p. [in Russian]
- Chetaev N. G. Ustoychivost’ dvizheniya [Stability of motion]. / N. G. Chetaev. – Moscow: Nauka, 1966. 207 p. [in Russian]
- Antonovskaya O. G. On the construction of quadratic Lyapunov function with given properties / O. G. Antonovskaya // Differential equations. – 2013. – V. 49. – № 9. – P. 1187-1191.
- Antonovskaya O. G. Determination of coefficients of a quadratic Lyapunov function with given properties / O. G. Antonovskaya // Differential equations. – 2016. – V. 52. – № 3. – P. 275-261.
- Sarybekov R.A. Ekstremal’nye kvadratichnye funktsii Lyapunova system uravneniy vtorogo poryadka [Extremal quadratic Lyapounov functions for systems of second order] / R.A. Sarybekov // Sib. Matem. Zhyrn. [Siberian Mathematical Journal] – 1977. – V. 18. – № 5. – P. 1159-1167.
- Antonovskaya O. G. O postroenii I primenenii uslovno-extremalnoy funktsii Lyapunova pri izuchenii ddinamiki sistemy s pomoshyu tochechnogo otobrazheniya ploskosti v ploskost’ [On a construction and use of extreme-conditional Lyapunov function when studying system dynamics by poinj mapping plane to plane] / O. G. Antonovskaya // Matematicheskoe modelirovanie I optimal’noe upravlenie [Mathematical modeling and optimal control] Vestnik NNGU. N. Novgorod: Izd-vo NNGU. – 2006. – № 3(32). – P. 110-117. [in Russian]
