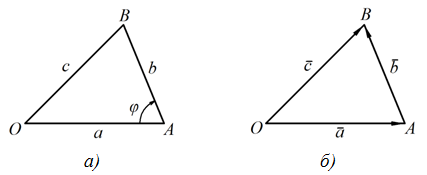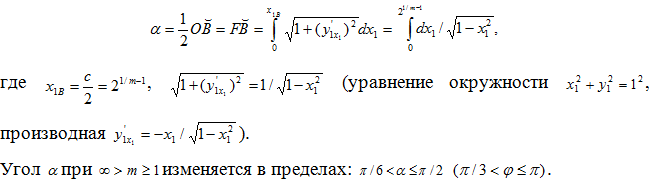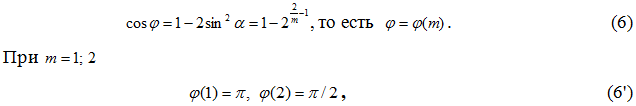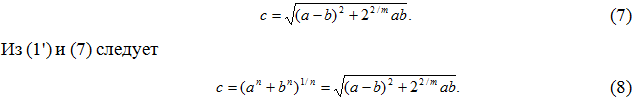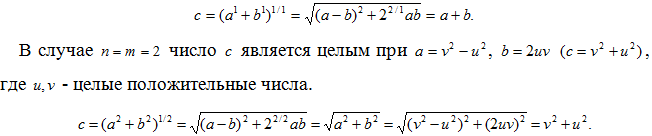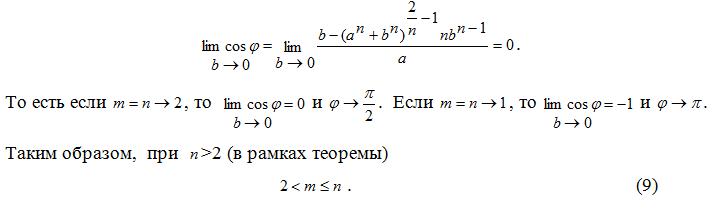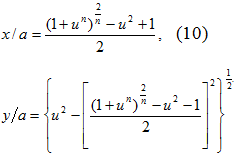TRIGONOMETRICAL REPRESENTATION OF REAL NUMBERS ELEMENTARY LAST (GREAT) P. FERMAT’S THEOREM PROOF
Соколов Г.М.
Профессор доктор технически наук, Поволжский государственный технологический университет
ТРИГОНОМЕРИЧЕСКОЕ ОТОБРАЖЕНИЕ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ. ЭЛЕМЕНТАРНОЕ ДОКАЗАТЕЛЬСТВО ПОСЛЕДНЕЙ (ВЕЛИКОЙ) ТЕОРЕМЫ П. ФЕРМА
Аннотация
Рассмотрено тригонометрическое отображение действительных чисел. На основании этого получено элементарное доказательств последней (великой) теоремы П. Ферма.
Ключевые слова: действительные, числа, теорема, Ферма.
Sокоlоv G.М.
Professor doctor of Technical Sciences, Volga State University of Technology
TRIGONOMETRICAL REPRESENTATION OF REAL NUMBERS ELEMENTARY LAST (GREAT) P. FERMAT’S THEOREM PROOF
Abstract
Trigonometrical representation of real numbers has been considered. On the grounds of that the elementary last (Great) P. Fermat’s theorem proof has been achieved.
Keywords: real, numbers, theorem, Ferma.
Теорема. Если a, b, c - положительные целые числа, то an+bn≠cn при где n - целое положительное число.
Напишем выражение
откуда
Смысл доказательства теоремы состоит в том, что следует установить, при каких целочисленных значениях n в выражении (1) совмещаются одновременно целые числа a, b, c.
Рассмотрим один из трех равнозначных случаев. Установим, при каких целочисленных значениях n в выражении (1) при целых a, b число c является целым. (В двух других при целых a, c в отношении целостной совместимости аналогично исследуется число b или при целых b, c исследуется a).
Следовательно, числа a,b,c выражают стороны треугольника (рис.1-а).
Рис. 1. Числа a, b, c как стороны треугольника
В векторной форме (рис. 1-б)
В дальнейшем вектор ![]() считаем постоянным и
считаем постоянным и ![]()
По теореме косинусов
откуда с учетом (1')
При n=1; 2 угол φ не зависит от a, b
При n=1 равенство (1) имеет вид
При n=2 в соответствии с теоремой Пифагора имеем
В обоих случаях годограф вектора ![]() является прямой, совпадающей с вектором
является прямой, совпадающей с вектором ![]() (прямые 1 (AK) и 2 (AG) на рис. 3).
(прямые 1 (AK) и 2 (AG) на рис. 3).
В остальных случаях (n≠1; 2) при постоянных n он является криволинейным.
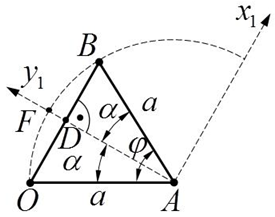
Рис. 2. К выводу тригонометрических выражений
Рассмотрим случай b=a. В равнобедренном треугольнике OAB (рис. 2) OB=c, OA=AB=a, α=φ/2 Обозначим m=n.
На основании (1') c=21/ma. Отсюда
Угол α в радианах при a=1 численно равен половине дуги окружности ![]()
При известных α и sin α можно определить все остальные тригонометрические функции.
Таким образом, тригонометрические функции и их углы являются функциями одной переменной m, выражающей действительные числа.
Напишем выражение
что повторяет случаи (4'), поэтому n=m=1; 2.
Заметим, что при m=const (cosφ=const) годограф вектора ![]() является прямой, совпадающей с линией вектора
является прямой, совпадающей с линией вектора ![]() (это прямые AB рис. 1, 2 ).
(это прямые AB рис. 1, 2 ).
На основании (4) теорема косинусов имеет вид
Число c в (8) при целых a,b является целым только тогда, когда подкоренное выражение является полным квадратом суммы, что может быть только при n=m=1; 2
В случае n=m=1
В остальном (при n≠1;2, m≠1;2) это условие не выполняется.
Таким образом, теорема доказана.
Установим диапазон изменения m для кривой с постоянным n.
Ясно, что верхний предел m=n при b=a.
Нижний предел находим из условия b→0. Рассмотрим ![]() , где на основании (4)
, где на основании (4) ![]() . И числитель, и знаменатель при b→0 стремятся к нулю, если n>1. Первая реализация правила Лопиталя приводит к результату
. И числитель, и знаменатель при b→0 стремятся к нулю, если n>1. Первая реализация правила Лопиталя приводит к результату
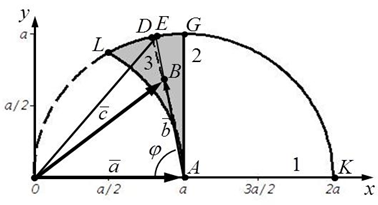
Пример. Рассмотрим случай n=3. На рис. 3 ![]() .
.
При 0<b≤a число m изменяется в пределах 2<m≤3 (кривая 3 (AD). Поэтому при целых значениях a,b число c целым быть не может.
Рис. 3. Геометрическая интерпретация функции ![]()
Кривая AD (n=3) построена по формулам (10), где ![]() ,
,
К примеру, для точки B (b=0,75a) по (10) имеем ![]() , а из (8) находится m=2,9393.
, а из (8) находится m=2,9393.
Теореме Ферма (∞>n≥2) соответствует область AGL (затемнена).
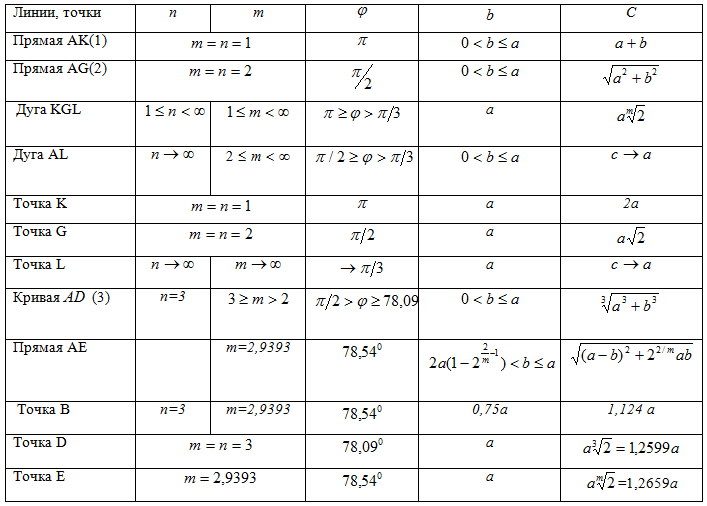
Результаты расчета приведены в таблице.
Таблица
Содержащиеся в таблице численные значения иллюстративно дополняют выполненное доказательство теоремы.
Литература
- Соколов Г. М. Общая последняя теорема П. Ферма (элементарное доказательство). Издание четвертое, переработанное. Йошкар-Ола, 2006. 36 с.
References
- Gennadiy Sokolov. Fermat’s last theorem (elementary proof). 4th edition, revised. Yoshkar-Ola. 2006. 36 s.