РОБАСТНАЯ МИНИМАКСНАЯ ЛИНЕЙНАЯ ЭКСТРАПОЛЯЦИЯ И ИНТЕРПОЛЯЦИЯ НЕСТАЦИОНАРНОГО ПРОЦЕССА В УСЛОВИЯХ ИНТЕРВАЛЬНОЙ НЕЧЕТКОСТИ МАТРИЦЫ СОСТОЯНИЯ СИСТЕМЫ С ОГРАНИЧЕННОЙ ДИСПЕРСИЕЙ
РОБАСТНАЯ МИНИМАКСНАЯ ЛИНЕЙНАЯ ЭКСТРАПОЛЯЦИЯ И ИНТЕРПОЛЯЦИЯ НЕСТАЦИОНАРНОГО ПРОЦЕССА В УСЛОВИЯХ ИНТЕРВАЛЬНОЙ НЕЧЕТКОСТИ МАТРИЦЫ СОСТОЯНИЯ СИСТЕМЫ С ОГРАНИЧЕННОЙ ДИСПЕРСИЕЙ
Аннотация
В статье рассматривается задача робастного прогнозирования и интерполяции процесса, когда ковариационные функции ошибок измерения и возмущений в процессе полностью неизвестны и принадлежат к некоторому множеству неотрицательно определенных функций. Рассматривается гарантирующая оценка, под которой понимается наилучшая оценка параметров полезного сигнала в смысле минимума среднеквадратической ошибки при наихудшем поведении ошибок измерений и возмущений с ковариационными функциями, принадлежащими множеству в условиях интервальной нечеткости в коэффициентах состояния и измерителя динамической слабо нестационарной системы с ограничениями на дисперсионную матрицу случайных процессов (ошибок измерения и возмущений) в предположении выполнимости аналогов слабой робастной теоремы В.Л. Харитонова для непрерывного случая. В зависимости от вида ограничений, т.е. характеристик множества, возникают разные подходы и методы решения задачи гарантирующего оценивания. В статье проведен обзор имеющейся литературы по вышеуказанной тематике.
Статья отличается от предшествующих публикаций тем, что в ней проведено аналитическое исследование задач прогнозирования и интерполяции при ограничении ковариационных функций ограничениями на их дисперсионные матрицы (дисперсии) в условиях интервальной нечеткости линейной динамической слабо нестационарной системы с параметрической неопределенностью задания матрицы состояния в рамках гурвицевой устойчивости (H-устойчивости) и интервальным уравнением наблюдения. В непрерывном случае получено выражение для нечетко-интервальной весовой функции, даны уравнения, которые надо решать при ее нахождении. Оценена точность прогнозирования и интерполяции и приводится сравнение с фильтрами, полученными по методу наименьших квадратов.
1. Введение
Исследуемые ниже вопросы рассматриваются в рамках линейной ковариационной теории оценивания для случая, когда ковариационные функции ошибок измерения и возмущений в полезном сигнале полностью известны и принадлежат некоторому множеству (здесь и ниже – множество неотрицательно определенных функций). Под гарантирующей оценкой понимается наилучшая оценка параметров полезного сигнала в смысле минимума среднеквадратической ошибки при наихудшем поведении ошибок измерения и возмущений с ковариационными функциями, принадлежащими множеству. В зависимости от вида ограничений, т.е. характеристик множества, возникают разные подходы и методы решения задачи гарантирующего оценивания (фильтрации).
В
показано, что если множество ковариационных матриц ограничено, замкнуто и выпукло, то при линейной модели поведения сигналов и ошибок измерения для дискретного случая наихудшее распределение ошибок измерения является гауссовым, оптимальное решение в классе нелинейных фильтров приводит к линейной фильтрации и в этой минимаксной задаче существует седловая точка.Аналогичный результат получен в
. В задача отыскания фильтра при ограничении дисперсии ошибок измерения сводится к двойственной задаче, и получен алгоритм численного отыскания фильтра. В ограничение задано по существу в виде ковариационной матрицы на весь процесс измерений и возмущений в целом. Близкие по постановке задачи рассмотрены также в , , , и многих других работах. В рассматривается минимаксная стационарная обработка информации для скалярного возмущения, в рассматривается минимаксная стационарная обработка информации, в стационарная в условиях интервальной нечеткости матрицы состояния системы с ограниченной дисперсией для скалярного возмущения, в нестационарная минимаксная задача с ограничениями на дисперсионную матрицу случайных процессов (ошибок измерения и возмущений).В данной статье рассматривается минимаксная задача в условиях робастной интервальной устойчивости в рамках H-устойчивости (гурвицевой устойчивости) в виде интервальной робастной нечеткости, присутствующей в коэффициентах состояния и измерителя динамической слабо нестационарной системы с ограничениями на дисперсионную матрицу случайных процессов (ошибок измерения и возмущений). Цель статьи – провести аналитическое исследование по совершенствованию математического моделирования нестационарных процессов с медленно меняющимися коэффициентами для решения задач гарантирующего оценивания (фильтрации), имеющие прикладное значение, например, в физике в области прогнозирования движения тел (наиболее характерно для космических объектов (КО)), вычисления для которых сопряжены с флюктуационными ошибками измерений, широко известна одна из классических проблем небесной механики – задача «трех тел», в задачах обнаружения космических объектов и их сопровождению с целью поддержания необходимой точности параметров орбиты КО, в своевременном обнаружении непрогнозируемых изменений параметров движения КО в процессе статистической обработки поступающих траекторных измерений и решении задачи уточнения параметров движения КО, в цифровой обработке параметров изображений в условиях априорной неопределенности и других прикладных задачах. Полученные результаты иллюстрируются примерами. Рассмотрен непрерывный случай процессов поведения сигналов, ошибок измерения и фильтрации, где это исследование проще и нагляднее.
2. Постановка задачи
Задана линейная непрерывная динамическая система объект-измеритель
с неопределенными непрерывными по t ∈ [t0,t1] матрицами ,
,
и
из интервалов
или в эквивалентной записи
где – полезный сигнал,
– возмущения в поведении сигнала,
– измеряемый сигнал,
- ошибки измерений.
При каждом фиксированном t ,
,
,
.
Матрицы ,
,
,
имеют соответcтвующие размерности. Пусть теперь
- матрица,
принимает всевозможные значения из компакта
при любом t из интервала наблюдения Ω=[t1,t2]. Модули матриц и матричные неравенства в (3) и далее понимаются поэлементно. Матрицы A0(t),bi0(t), C0(t),di0(t) и ΔA(t),Δbi(t),ΔC(t), Δdi(t) составлены из середин и полудлин интервалов (4), границами
,
,
,
,
,
,
,
интервалов служат известные непрерывные матричные функции cоответствующих размерностей. Систему (1), (2) при A(t)=A0(t), bi(t)=bi0(t), C(t)=C0(t) и di(t)=di0(t) назовем центральной.
Предполагается, что система (1), (2) в отсутствие ошибок измерения и возмущений наблюдаема. Для стационарной системы, когда ,
, необходимое и достаточное условие наблюдаемости , , заключается в том, что
Опираясь далее на качественную сторону теоремы Харитонова для слабо стационарных систем, будем предполагать, что центральные матрицы A0(t), b0(t), d0(t) постоянны, а возмущения ΔA(t), Δbi(t), ΔC(t), Δdi(t) удовлетворяют условиям типа
с параметрами ,
,
,
, обеспечивающие робастную устойчивость слабо стационарной интервальной системы (1), (2) в рамках гурвицевой устойчивости
Известно, что возмущения ηi(t), i = 1,…,N и ошибки измерений ξi(t), j = 1,…,M представляют собой среднеквадратично интегрируемые, некоррелированные случайные процессы с нулевыми математическими ожиданиями M[ηi(t)] = 0, M[ξi(t)] = 0, i = 1, …, N, j = 1, …, M. Известна корреляционная функция (t) процесса ξ0(t), t, τ∈Ω.
Относительно всех остальных процессов известно, что дисперсионные матрицы их ограничены положительно определенными матрицами, т.е.
(Здесь неравенство A > B (A > B) для любых симметричных матриц A и B понимается в том смысле, что разность A-B является неотрицательно (положительно) определенной матрицей). Каждое из ограничений в (4.2) определяет множества ,
, так что
есть прямое произведение первых множеств.
По измерениям ,
оценивается скаляр
, где q – заданный вектор-столбец q ∈ Rn. Оценка ищется в классе линейных функционалов
При s∈Ω решается задача интерполяции при t1≤s≤t2, при s∉Ω задача экстраполяции или прогнозирования (s>t2). Точности этих последних задач одинаковы.
Поэтому ограничимся только прогнозом. Пусть – фундаментальная матрица системы
Предположим, что априорное значение фазового вектора в любой момент времени t неизвестно. Поэтому оценка
должна быть несмещенной
В силу наблюдаемости множество функций
, удовлетворяющих (6), не пусто. Множество весовых функций
, удовлетворяющих условию (6), обозначим как λ(s),
А фундаментальную матрицу центральной системы
через W0(t, τ).
Очевидно матричное неравенство
Оценим максимальные отклонения от фундаментальной матрицы центральной системы по всем допустимым
не превосходящие
с учетом равномерного уменьшения норм матриц ΔA(t),Δbi(t),ΔC(t), Δdi(t) на отрезке Ω.
Используя (7) совместно с матричными экспонентами для описания пучка траекторий слабо стационарных интервальных однородных систем, можно получить оценки искомых отклонений со стационарными границами интервалов (A0(t) = A0, ΔA(t) = ΔA) в виде
Последнее означает, что оценка (8) уменьшается, когда норма матрицы равномерно на t∈Ω убывает, т.е.
.
Аналогичное поведение в оценках отклонений наблюдается и в нестационарном случае, когда ||ΔA(t) ||→0. Итак, для стационарного случая имеем оценку
Можно показать , что для неоднородных слабо стационарных систем характер изменения искомых оценок в отклонениях фундаментальной матрицы системы (1), (2) не меняется, когда матричные нормы в отклонениях удовлетворяют условиям типа (4b). C учетом полученного вывода можно доказать, что характер изменения в отклонениях весовой функции минимаксного фильтра от номинального или центрального фильтра имеет аналогичное поведение c учетом условия несмещенности (6).
Если ввести относительную матричную невязку по максимальным отклонениям в фундаментальной матрице системы (1),(2) в виде и взять ее верхнюю оценку по матричной норме
, где 0<γW<1, то получим изменение по матричной норме для искомой весовой функции минимаксного экстраполятора от номинального фильтра в прежнем виде
. С учетом сделанной оценки cправедливо соотношение
С учетом (6), меняя порядок интегрирования при вычислении влияния возмущения, получим то, что дисперсия ошибки оценивания имеет вид:
где
Здесь
Таким образом, дисперсия ошибки оценивания есть функционал от весовой функции
и корреляционных функций
т. е.
Оптимальная гарантирующая оценка находится минимизацией наибольшего значения дисперсии
для наихудшего поведения возмущений и неопределенных ошибок измерения в рамках ограничений, т.е.
В дальнейшем предположим, что составляющая ошибок с известной корреляционной функцией представляет собой “белый шум”, т.е.
где – известная неособенная (положительно определенная) матрица интенсивности “белого шума”.
Приведенная постановка задачи характерна, в частности, для задач определения движения космического объекта, самолета по радиолокационным либо оптическим измерениям. Здесь флюктуационные (шумовые) ошибки измерений носят характер “белого шума”. Остальные составляющие ошибок и возмущений носят неопределенный характер – известна их дисперсия или в более общем случае дисперсионная матрица, т.е. эллипсоид, содержащий эти ошибки при фиксированном уровне доверительной информации α=0,1.
3. Общее решение задачи
Начнем решение задачи с внутренней максимизации выражения (5) для дисперсии ошибок фильтрации. Для этого нам понадобится следующая теорема
.Теорема 1. Пусть ξ(t) – случайный (в общем случае векторный) процесс. На множестве случайных функций ξ(t),t∈ Ω определен линейный функционал
Относительно процесса ξ(t) известно, что его дисперсионная матрица ограничена, т.е. множество его ковариационных функций определяется неравенством
Κ(t) – положительно определенная матрица для любого .
Имеет место оценка дисперсии оценивания
При этом точная верхняя грань достигается на процессе вида ξ(t)=μφ(t), где μ – случайная величина: M[μ]=0,M[μ2]=1, φ(t) – детерминированная векторная функция
такая, что
т.е. K(t,t)=φ(t)φT(t).
Там, где g(t) = 0 в (16) имеет место знак равенства и
Доказательство теоремы приведено в .
Множество функций φ(t), на которых достигается экстремум, очевидно является выпуклым, ограниченным и замкнутым в нормированном пространстве с нормой
Согласно теореме 1 максимальное значение дисперсии оценивания в (5) при фиксированной весовой функции принимает вид:
При этом максимизирующие возмущения можно записать в виде квазидетерминированных случайных процессов
где случайные величины μi,νi не коррелированы между собой и
Неслучайные функции φi(t) и ψi(t) ограничены:
При этом имеет место знак равенства там, где :
Из (1) и представления случайных функций следует, что полезный сигнал можно записать в виде
Введем матрицы
Тогда измеряемый сигнал принимает вид
где
Таким образом, задача минимизации сводится к совместной оценке параметров ,
,
.
Введем еще более краткую запись:
где
Обозначим также
Имеет место:
Теорема 2. Минимизирующая весовая функция имеет вид:
Дисперсия ошибки оценивания имеет вид:
Здесь введены обозначения:
, E– единичная матрица размера N +M.
Доказательство этой теоремы приведено в Приложении.
Выражения (26), (27) вместе с выражениями (20), (21), (23), (24) и (27) полностью описывают искомый робастный фильтр и гарантированное качество фильтрации. При этом надо иметь в виду следующее. На множествах ,
там, где соответственно
и
определяется вид функций φi(τ) и ψi(τ) таких, что в неравенствах (19) имеет место знак строгого неравенства. Эти множества характеризуют те интервалы измеряемой информации, которая не используется (отбраковывается) в фильтре. Это цена за недостаточно полное априорное описание неопределенных ошибок и возмущений. Если существует решение указанных уравнений для
и функций φi(τ), ψi(τ), то существует и робастная в указанном выше нечетко - интервальном смысле седловая точка. Отметим, что критерий качества является квадратичным по робастной весовой функции и линейным по корреляционной функции возмущений.
4. Пример
Рассмотрим простейший случай, часто встречающийся на практике, когда на интервале наблюдения измеряемый процесс изменяется по линейному закону
, 0<γ<1, т.е.
. Интервальная нечеткость модели задается параметром нечеткости
. Ошибка измерений содержит флюктуационную ошибку (“белый шум” с матрицей интенсивности
) и неопределенную ошибку с дисперсией, ограниченной
.
Здесь ,
,
,
Из (25) следует выражение для оптимальной весовой функции:
где
,
,
где
– интервал используемой информации. Так как
,
.
где ,
, τк и τн – интервалы используемой информации соответственно в конце и начале интервала обработки. В середине интервала информация не используется.
Рассмотрим I случай.
Здесь ,
и весовая функция такая же, как и при отсутствии неопределенных ошибок (независимо от их величин)
Поскольку φ(t)=1, то должно быть для всех
.
А это возможно, если и, следовательно, время экстраполяции относительно середины интервала обработки
. Это решение задачи интерполяции для третьей части всего интервала обработки.
Рассмотрев второй и третий случаи можно сделать вывод
, что решение задачи интерполяции и прогнозирования в зависимости от соотношения ошибок в измерениях реализует все возможные ситуации. Возможно отбрасывание информации, как в конце наблюдения, так и в середине интервала. Интересно провести сравнение по гарантированной точности оценивания с робастным фильтром, настроенным только на флюктуационные ошибки, каковым является фильтр, полученный по методу наименьших квадратов в традиционном толковании. Поведение функций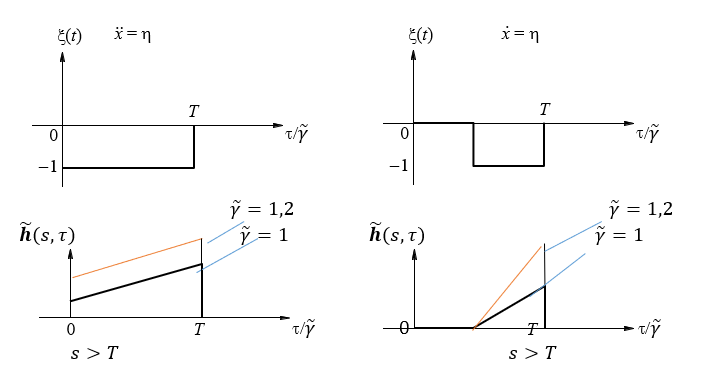
Рисунок 1 - Возможные случаи поведения весовой функции h~(s,τ) при заданном параметре интервальной нечеткости γ ̃=1,2 и γ ̃=1
Фильтр, настроенный только на флюктуационные ошибки, имеет вид
и дает дисперсию суммарных ошибок
При минимаксная интерполяция не дает выигрыша. Предельный выигрыш получается χ=0 (отсутствии флюктуационных ошибок)
Наибольший выигрыш получается при оценке полезного сигнала в конце наблюдения равен
. Все случаи поведения
,
и
изображены на рисунке 1 в масштабе времени
.
5. Пример
В качестве сравнения приведем также пример, позволяющий сравнить фильтры для устойчивой и неустойчивой слабостационарной системы первого порядка с заданной степенью устойчивости η. Рассмотрим случай неустойчивой системы первого порядка со степенью устойчивости η, измеряемый сигнал которой содержит неопределенную ошибку с дисперсией, ограниченной Dξ≤σ2 и спектральной плотностью . О корреляционной функции возмущения u(t) известно лишь ограничение на его дисперсию Mu2≤au т. е.
и быть может ограничение на область сосредоточения его спектральной плотности h(λ)=0 при λ∈Λ, Λ – заданное подмножество оси частот. Допущения (4б) обеспечивают переход системы фильтрации (уравнения (25), (26)) в стационарный режим. Обозначим . Введем обозначение
где матричная функция, порожденная нечетко-интервальной скалярной функцией
, где
– заданное нечеткое число, C0, b0 - постоянные матрицы центральной системы (1), (2). Можно показать
где ,
.
Корреляционный момент ( отнесенный к τ2) удовлетворяет уравнению
Частотная характеристика минимаксного робастно устойчивого интервального фильтра для имеет вид
а для -
,
где
Субоптимальный робастный минимаксный фильтр, получающийся при λ→∞ в обоих случаях имеет частотную характеристику
При этом проигрыш по отношению к среднеквадратическим не превышает 10%.
При малых λ→0 для устойчивой системы интервал неопределенности в оценке корреляционноцй функции увеличивается приблизительно на η.
Это обстоятельство важно для практической реализации фильтра, решающего многокритериальную задачу.
6. Заключение
Представленная работа посвящена вопросу робастного прогнозирования и интерполяции процесса, когда ковариационные функции ошибок измерения и возмущений в процессе полностью неизвестны и принадлежат к некоторому множеству неотрицательно определенных функций в условиях робастной интервальной устойчивости в рамках H-устойчивости (гурвицевой устойчивости) в виде интервальной нечеткости присутствующей в коэффициентах состояния и измерителя динамической слабо нестационарной системы с ограничениями на дисперсионную матрицу случайных процессов (ошибок измерения и возмущений). В предположении выполнимости аналогов слабой робастной теоремы В.Л. Харитонова для непрерывного случая
Результаты данного исследования апробированы на примере линейно слабо стационарно изменяющегося процесса в виде полинома первой степени с интервальным коэффициентом нечеткости. Проведено сравнение искомого фильтра по гарантированной точности оценивания с фильтром, настроенным только на флюктуационные ошибки, каковым является фильтр, полученный по методу наименьших квадратов в традиционном толковании. Построены графики всех возможных случаев в поведении весовой функции минимаксного робастно-устойчивого фильтра первого и второго порядка при заданном параметре интервальной нечеткости, присутствующего в модели объекта, а также приведено сравнение фильтров для устойчивой и неустойчивой слабостационарной системы первого порядка с заданной степенью устойчивости η. Описанные в статье алгоритмы математического прогнозирования могут найти отражение не только в различных областях физики и других естественных наук (например, для наилучшей оценки параметров полезного сигнала), но и в гуманитарной сфере - при описании поведения систем с динамическим хаосом (эволюционизм в природе, теория фракталов сложных структур в результате самоорганизации, теория катастроф, лингвистическая прогностика и пр.). Автором рассмотрены алгоритмы вычислений в теории управления и самоорганизации, построенные на базе математических моделей и вычислительного эксперимента. Входные данные для оценки поведения нестационарного процесса в линейной ковариационной теории описывается системой обыкновенных дифференциальных уравнений.
