ВЛИЯНИЕ ВЕТРА НА КОНВЕКТИВНОЕ ТЕЧЕНИЕ ВЯЗКОЙ НЕСЖИМАЕМОЙ ВЕРТИКАЛЬНО ЗАВИХРЕННОЙ ЖИДКОСТИ

В настоящее время описание процессов в жидких и газообразных средах представляет интерес для исследования. Развитие технологий и возможность их применения в производстве играют важную роль в жизни современного общества. Исследования, направленные на изучение и описание течений жидкости, используются в динамике плазмы, разработке хладогентов и т. п.

Для описания течения жидкостей применяются математические модели. Традиционно используется система уравнений тепловой конвекции

В статье представлены результаты анализа аналитических решений исходной системы дифференциальных уравнений в частных производных. Нетривиальной задачей является выбор граничных условий, от которых в существенной степени зависят свойства течения. В статье исследованы случаи при условии прилипания на границе жидкости с твердой поверхностью

Рассматривается течение вязкой несжимаемой жидкости в горизонтальном слое постоянной толщины h. Конвективное течение вязкой несжимаемой жидкости традиционно описывается следующей системой уравнений

- уравнение Навье-Стокса в приближении Буссинеска:

- уравнение теплопроводности:

- уравнение несжимаемости жидкости:

Здесь 

Имеются пять уравнений (1)-(3) и 4 неизвестных 

При подстановке представления (4) в уравнение несжимаемости (3) уравнение (3) удовлетворяется тождественно. Проблема с переопределением разрешена.

После неcложных преобразований получаем итоговую систему уравнений:

В итоге система уравнений в частных производных (1)-(3) превращается в систему обыкновенных дифференциальных уравнений (5) для нахождения неизвестных функций 

Учитывая, что 

Общее решение системы (5) представляет собой набор полиномиальных функций не выше четырнадцатой степени.

В решение системы (5) входят пятнадцать постоянных интегрирования, для их определения потребуются граничные условия. Будем рассматривать течение в слое жидкости толщины h, нижней границе которого соответствует значение z = 0 вертикальной координаты. Положим, что на нижней границе выполняется условие прилипания, а также известно распределение температуры:

На верхней же границе (при z = h) положим известными распределение поля скорости, температуры и давления:

Здесь W – значение фоновой скорости течения жидкости на верхней поверхности слоя, угол 

По известным краевым условиям определим постоянные интегрирования, находя таким образом частное решение системы (5). Для упрощения анализа выполнен переход к безразмерной координате Z, произведя замену 

где 

4.1. Анализ скорости v

Первоначально разберём свойства скорости v, определяемой выражением (6).

Проведем для дальнейшего удобства некоторые простые преобразования и введем ряд соответствующих обозначений:

При этом представим функцию 

где

а индекс i коэффициента ai соответствует члену i-ой степени (по вертикальной координате Z).

Так же заметим зависимость коэффициентов a6, a3 от коэффициентов  a2, a5

Тогда функция f(Z) перепишется в виде

В итоге скорость v будет описываться следующим выражением:

Как ранее было сказано, скорость v принимает нулевое значение на границе слоя Z=0, что видно из структуры выражения (8). Поэтому далее будем искать точки обращения функции f в нуль внутри слоя, таким образом определять застойные точки течения и возможные противотечения в слое [0,1].

Необходимо рассмотреть различные комбинации значений констант  для анализа поведения скорости (8). Заметим, что случаи 

Группа I: лишь один коэффициент из  ai (i = 0,1,2,5) равен нулю

I.1) Пусть

Наибольшее число внутренних застойных точек равняется двум, что проиллюстрировано на рисунке 1.

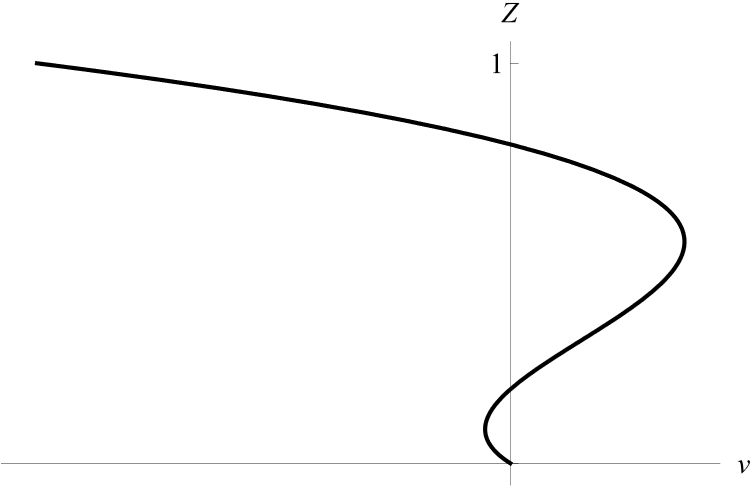
Рисунок 1 - Профиль скорости v при a5 = 0, a0a1a2 ≠ 0

DOI:10.60797/IRJ.2024.143.180.1

I.2) Пусть 

Этот случай реализуется при A=0 Тогда компонента скорости v имеет не более двух нулевых точек внутри рассматриваемого слоя

[9]

(см. рисунок 2).

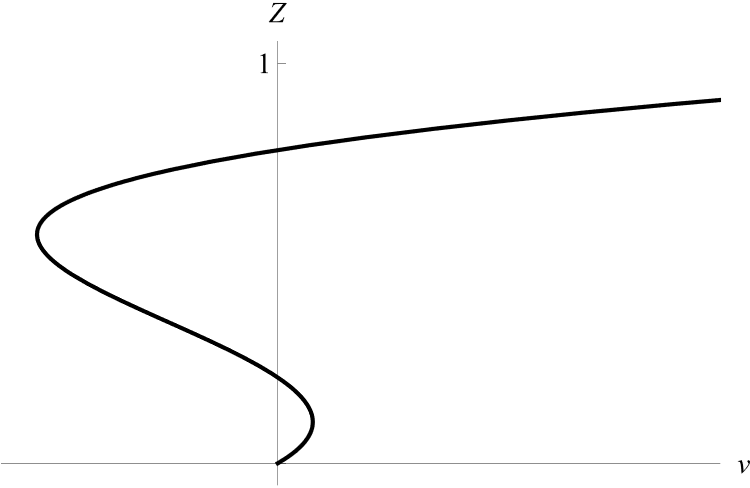
Рисунок 2 - Профиль скорости v при a2 = 0, a0a1a5 ≠ 0

DOI:10.60797/IRJ.2024.143.180.2

I.3) Пусть 

Такая ситуация возможна лишь при ненулевых значениях параметров

$A,B,S_1,\Omega$

 (в противном случае автоматически получаем a2 = a5 = 0). Аналогично предыдущему

[9]

, компонента скорости v имеет внутри слоя не более двух застойных точек (см. рисунок 3).

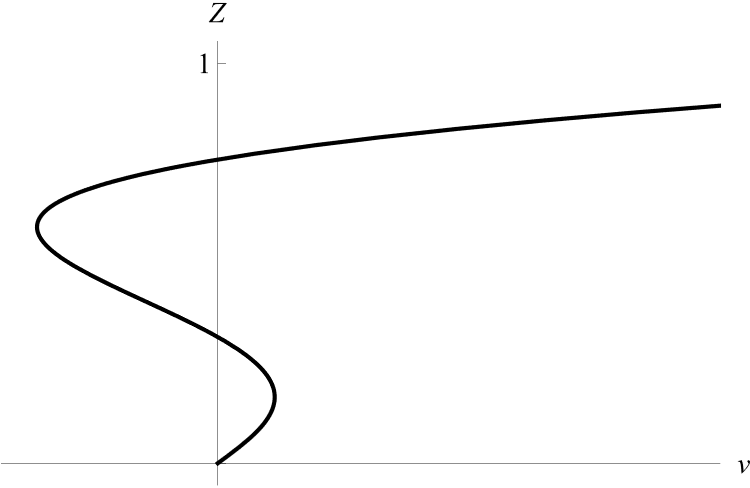
Рисунок 3 - Профиль скорости v при  a1 = 0, a2a5a0 ≠ 0

DOI:10.60797/IRJ.2024.143.180.3

I.4) Пусть

Этот случай возможен при W = 0 и/или

Исследуя монотонность этой функции, делаем вывод, что внутри исследуемого слоя скорость v также может иметь не более двух нулей (см. рисунок 4).

Рисунок 4 - Профиль скорости v при a0 = 0, a1a2a5 ≠ 0

DOI:10.60797/IRJ.2024.143.180.4

Из приведенных выше рассуждений видно, что во всех случаях, когда только один из коэффициентов 

$a_i(i=0,1,2,5)$

 равен нулю, скорость v имеет одинаковое максимальное число точек застоя, равное двум (см. рисунок 1-4).

Группа II: только два коэффициента из 

II.1) Пусть

Такая комбинация осуществима при A=0, B=0 и/или 

$\Omega =0.$

Функция f принимает линейный вид, и, очевидно, она имеет внутри слоя

$0\le Z\le 1$

 лишь один нуль, что проиллюстрировано на рисунке 5.

Рисунок 5 - Профиль скорости v при a2 = a5 = 0, a0a1 ≠ 0

DOI:10.60797/IRJ.2024.143.180.5

II.2) Пусть

Это возможно при 

$W\sin \phi +\frac{Ag{h}^3\beta }{8v}-\frac{h^2{S}_1}{2v}=0\text{ и }B=0\text{ и/или }\Omega =0\text{. }$

 В слое не может существовать более одной нулевой точки скорости v (см. рисунок 6).

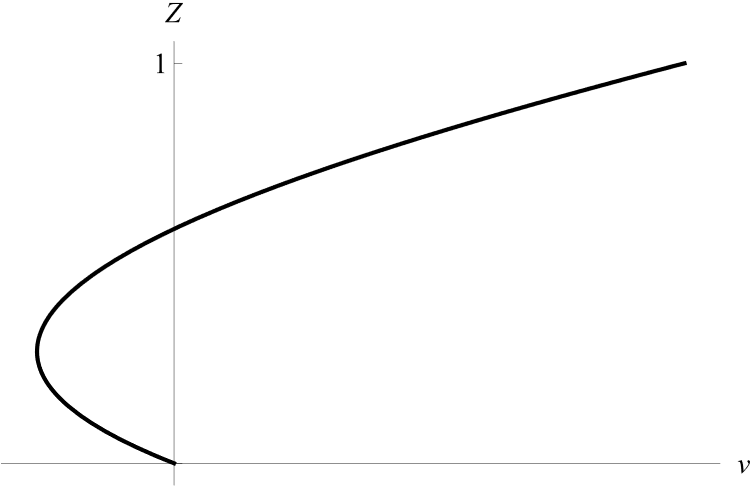
Рисунок 6 - Профиль скорости v при a0 = a5 = 0, a1a2 ≠ 0

DOI:10.60797/IRJ.2024.143.180.6

II.3) Пусть

Этот случай возможен при 

Скорость v имеет не более двух нулей в слое 

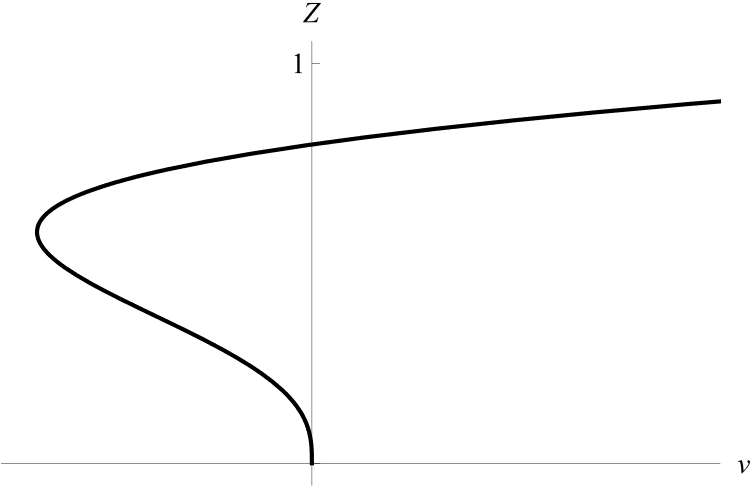
Рисунок 7 - Профиль скорости v при a0 = a1 = 0, a2a5 ≠ 0

DOI:10.60797/IRJ.2024.143.180.7

II.4) Пусть

$a_1=a_2=0,a_0{a}_5\ne 0$

Данная ситуация реализуется при 

Исследовав монотонность функции, выясняем, что f монотонна на всем промежутке (0,1) и поэтому может иметь лишь один нуль внутри рассматриваемого слоя. Соответствующий профиль скорости v изображен на рис. 8.

Рисунок 8 - Профиль скорости v при a1 = a2 = 0, a1a5 ≠ 0

DOI:10.60797/IRJ.2024.143.180.8

II.5) Пусть

Этот случай возможен при 

Рисунок 9 - Профиль скорости v при a0 = a2 = 0, a1a5 ≠ 0

DOI:10.60797/IRJ.2024.143.180.9

II.6) Пусть

Этот случай осуществим при 

$A\ne 0,B\Omega =0,\frac{h^2{S}_1}{2v}=\frac{{\mathrm{Agh}}^3\beta }{4v}$

. Функция строго монотонна на этом интервале (0,1) и имеет одну нулевую точку (см. рисунок 10).

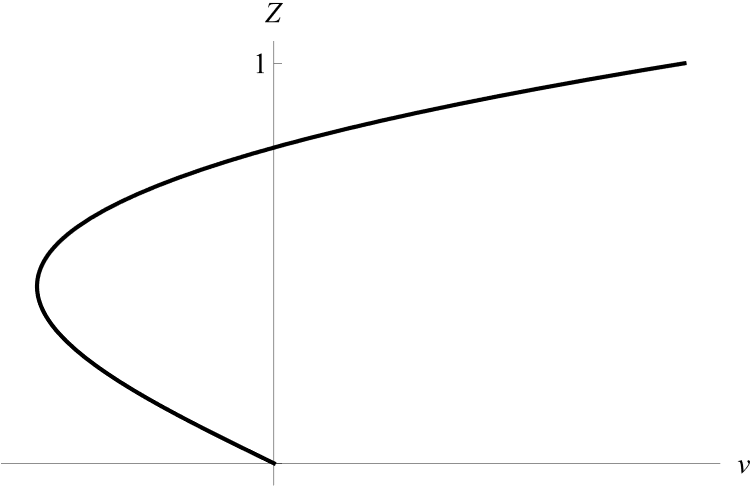
Рисунок 10 - Профиль скорости v при a1 = a5 = 0, a0a2 ≠ 0

DOI:10.60797/IRJ.2024.143.180.10

Заметим, что в случаях II.1)-II.6) (и на рисунках 5-10 соответственно) прослеживается закономерность: для случаев с двумя (из четырех) равными нулю параметрами 

$a_i(i=0,1,2,5)$

  скорость v имеет внутри исследуемого слоя лишь одну застойную точку.

Группа III: ровно три коэффициента из

III.1) Пусть

Тогда 

$A=0,B\Omega \ne 0,\frac{Bg{h}^5\beta \Omega }{120v\chi }=-\frac{h^2{S}_1}{2v},W\sin \phi =-\frac{5Bg{h}^5\beta \Omega }{2016v\chi }$

. На отрезке [0,1] полином f строго монотонен и при этом имеет экстремум в точке Z=0, то есть функция f, преодолевая Z=0 далее либо возрастает, либо убывает, не пересекая ось Z. Профиль скорости v в этом случае представлен на рисунке 11.

Рисунок 11 - Профиль скорости v при a0 = a1 = a5 = 0, a2 ≠ 0

DOI:10.60797/IRJ.2024.143.180.11

III.2) Пусть

Этот случай реализуется при 

$A\ne 0,B\Omega =0,\frac{h^2{S}_1}{2v}=\frac{Ag{h}^3\beta }{4v},W\sin \phi =\frac{Ag{h}^3\beta }{8v}$

. На промежутке (0,1) нулей функция не имеет. Тогда скорость v в слое 

$Z\in [0,1],$

 имеет единственный нуль на границе Z=0 рассматриваемого слоя и ни одного нуля внутри (см. рисунок 12).

Рисунок 12 - Профиль скорости v при a0 = a1 = a5 = 0, a2 ≠ 0

DOI:10.60797/IRJ.2024.143.180.12

Заметим, что случаи III.3) 

$a_1=a_2=a_5=0,a_0\ne 0$

 и III.4) 

$a_0=a_2=a_5=0,a_1\ne 0$

 обсуждались выше ввиду их тривиальности.

Аналогично предыдущим выводам, подведем итог, что для вариантов с тремя нулевыми коэффициентами и 

Группа IV: ни один из коэффициентов

В эту группу попадает только один случай, он вынесен в классификацию этой группы. Это наиболее общий случай из исследуемых. Это возможно при 

$A\ne 0,B\Omega \ne 0,S_1\ne 0,W\sin \phi \ne 0$

, но не только при этом сочетании значений параметров. Функция f из выражения (7) является линейной комбинацией трех монотонных на исследуемом интервале функций. Из чего следует, что компонента скорости v имеет внутри рассматриваемого слоя 

$Z\in [0,1],$

  не более трех точек застоя [9]. Данный факт проиллюстрирован на рисунке 13.

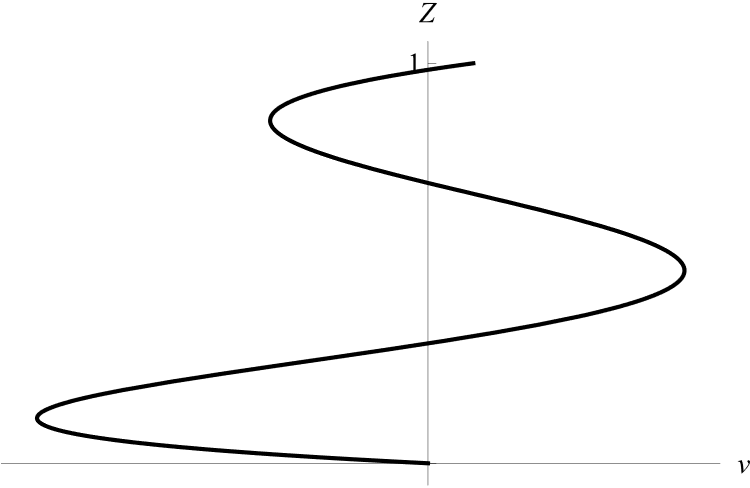
Рисунок 13 - Профиль скорости v при a0 a1 a2a5 ≠ 0

DOI:10.60797/IRJ.2024.143.180.13

Рассмотрев различные вариации значений параметров для скорости  v, получили, что компонента скорости может как не иметь нулей в рассматриваемом слое вовсе, так и иметь не более трех застойных точек внутри слоя, таким образом разделяя его на четыре подслоя с возможной сменой направления течения (см. рисунок 13).

Перейдем к анализу компоненты u скорости Vx, описываемой решением (6). Для скорости u справедливо представление 

Произведем замену для упрощения дальнейших рассуждений.

где индексы i коэффициентов bi  соответствуют степени вертикальной координаты Z и

Заметим, что не все коэффициенты являются независимыми

Тогда функция g преобразуется к виду:

В итоге компонента скорости u представима в виде:

Из структуры выражения (9) видно, что скорость u принимает нулевое значение на нижней границе исследуемого слоя Z=0 Для нахождения остальных нулевых точек, необходимо подробнее рассмотреть поведение функции g. Как и при анализе скорости v, можно рассмотреть все возможные сочетания значений коэффициентов 

Скорость u (9) может принимать нулевое значение внутри слоя, только если полином g имеет на интервале (0,1) действительные корни.

Компонента скорости u может иметь внутри слоя 

$Z\in [0,1]$

 не более шести застойных точек (см. рисунок 14).

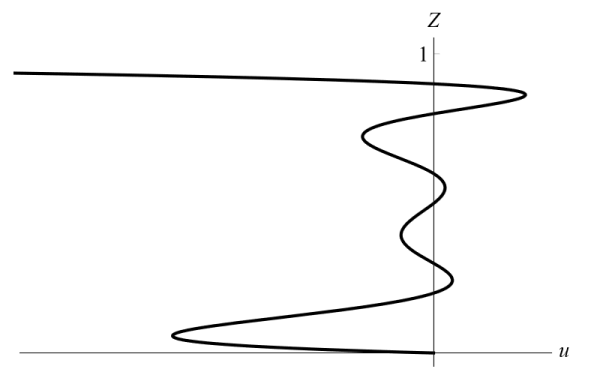
Рисунок 14 - Профиль скорости u при b0b1b2b3b4b5b8  ≠ 0

DOI:10.60797/IRJ.2024.143.180.14

В данной статье рассмотрена краевая задача, описывающая конвективное течение вязкой несжимаемой вертикально завихренной жидкости в горизонтальном слое. Получено ее точное решение при условии прилипания жидкости на нижней границе слоя. Рассмотрено возможное поведение поля скорости течения в зависимости от задаваемых на верхней границе исследуемого слоя жидкости условий. Было показано, что в слое жидкости могут возникать области с обратным течением, причем в рассматриваемом слое может существовать не более четырех подслоев с разным направлением течения. Показано, что число застойных точек (и соответственно подслоев) может меняться в зависимости от значений параметров краевой задачи.  Также было показано, что могут существовать области, в которых касательное напряжение меняет свой тип – с растягивающего на сжимающее и наоборот. В ходе работы также были получены аналитические выражения для компонент полей температуры и давления. Анализ этих выражений не вошел в содержание данной статьи.