КОГНИТИВНО-ВИЗУАЛЬНЫЙ ПОДХОД К ОБУЧЕНИЮ МАТЕМАТИКЕ СТУДЕНТОВ КОЛЛЕДЖА

Современные трансформационные процессы, обусловленные цифровизацией и информатизацией общества, оказывают значительное влияние на систему среднего профессионального образования (СПО). Работодатели предъявляют новые требования к выпускникам колледжей, акцентируя внимание на практическом интеллекте, способности к решению производственных задач, адаптивности, владении современными технологиями и методиками.

Следует отметить, что математические знания и умения необходимы при освоении любых специальностей. Они являются основой для изучения профессиональных дисциплин, развивают мышление, логику и другие психические процессы личности, что способствует как профессиональному, так и личностному росту будущих специалистов. Интеграция математических знаний, умений и их применение в будущей профессиональной деятельности, а также стремление к саморазвитию в профессиональной области – это залог высокой конкурентоспособности и профессиональной компетентности квалифицированного специалиста

Для формирования математической компетентности студентов колледжа, представляющей собой совокупность знаний, умений и навыков, обеспечивающих способность применять математические методы и инструменты в профессиональной деятельности, необходимы инновационные методы организации учебного процесса, что подразумевает пересмотр структуры и объема содержания математической подготовки, а также создание специальной обучающей среды, которая будет гибкой и адаптивной, будет учитывать потребности и возможности каждого студента и способствовать повышению качества и результативности образовательного процесса.

Развитие технологий оказывает значительное влияние на процессы обучения и передачи знаний, кардинально меняя подходы, формат, методы и доступность. К ключевым аспектам отнесем: доступность информации, онлайн-обучение, интерактивные технологии, персонализированное обучение, сотрудничество и коммуникации, развитие критического мышления, гибкость и самоорганизация. В целом, технологии обогащают процесс обучения, делая его динамичным и адаптивным.

Исследуя значимость визуальной составляющей в современных образовательных технологиях, можно констатировать, что визуальные элементы играют заглавную роль в образовательных технологиях, так как они способны улучшить процесс обучения и делают информацию более доступной и понятной. Визуальные элементы эффективно организуют восприятие информации, повышают мотивацию и вовлеченность студентов, позволяют преподавателю адаптировать свои подходы к обучению, повышают уровень запоминания, упрощают сложные понятия, улучшают коммуникацию, способствуют созданию более инклюзивной образовательной среды

Важность визуальных элементов в формировании математической компетентности студентов колледжа проявляется в их способности визуализировать сложные и абстрактные концепции, делая их более доступными и понятными. Более того, визуальные элементы стимулируют креативное мышление и воображение студентов. Они помогают студентам увидеть взаимосвязи между различными концепциями и идеями, что способствует развитию аналитических и критических навыков. Визуальные элементы также способствуют углубленному анализу информации и помогают студентам видеть более широкую понятийную картину, что способствует развитию их критического мышления.

Визуальные технологии охватывают все инструменты, связанные с восприятием изображения – от простых печатных материалов до сложных проекционных экранов и 3D-технологий. Они служат своего рода «говорящими» сигналами для человеческого восприятия. Благодаря визуальным технологиям обучающиеся эффективно воспринимают информацию, представляя ее в удобной, понятной и компактной форме. В нынешнюю эпоху «визуалов», ставшую популярной с развитием гаджетов, влияние таких технологий становится все более значимым. Техники визуализации учебной информации включают в себя различные методы и инструменты, которые помогают лучше воспринимать и усваивать материал: инфографика, таймлайн, интеллект-карта, скрайбинг, кроссенс, облако слов и др.

Использование, например, инфографики для обобщения сложных математических тем или формул может помочь студенту быстро усваивать и запоминать основные идеи. Флипчарты, маркерные доски и другие визуальные средства могут быть использованы в формате групповых заданий, что способствует взаимодействию между студентами и качественному обсуждению математических концепций. Использование визуальных шаблонов для решения задач, например, алгоритмов для решения уравнений, помогает систематизировать процесс мышления и облегчает понимание. Демонстрация математических процессов (видео или анимация) помогут студентам лучше понять последовательность операций и логику математических решений. Использование технологий дополненной и виртуальной реальности позволяет изучать математические понятия через взаимодействие с трехмерными моделями и сценариями, что делает процесс обучения более увлекательным и интуитивно понятным. Графическое представление данных (например, использование графиков, диаграмм, столбчатых диаграмм) помогает визуализировать данные и выявлять тенденции, что облегчает анализ и интерпретацию информации и является важной частью математического мышления. Визуальные схемы, структурные схемы или модельные репрезентации, помогают студентам понять более абстрактные математические концепции, например, свойства геометрических фигур или алгебраические выражения. Интерактивные визуализации (программное обеспечение и приложения), такие, как геометрические редакторы и калькуляторы, позволяют студентам манипулировать в реальном времени, что способствует глубокому пониманию математических понятий и помогает развить навыки решения задач.

В настоящее время широкое распространение получил термин «визуальное мышление», то есть зрительно-наглядное, означающее по Р. Арнхейму «мышление посредством визуальных (зрительных) операций»

Визуальное мышление задает уникальный способ обработки и осмысления информации, при котором основной акцент делается на визуальные представления и образы. Визуальное мышление позволяет воспринимать, организовывать и анализировать данные через визуальные элементы.

Визуальные образы не иллюстрации к мыслям автора, а итоговый результат самого процесса мышления. В отличие от традиционного применения средств наглядности, работа визуального мышления – это деятельность разума в особой среде, которая позволяет преобразовывать информацию, меняя формат и осмыслить связи и отношения между ее объектами

Связь визуального мышления с внешней практической деятельностью описывается с помощью уточненной концепции интериоризации. Умственная деятельность, согласно этой концепции, при определенных условиях поэтапно осуществляется, отталкиваясь от внешней предметной деятельности. Можно выделить три этапа формирования идеального образа сознания. Первый – снятие операционной копии с объекта, его моделирование в системе предметно-практических операций. В этом случае форма эталонного предмета как бы превращается в форму деятельности, функционально отражающую внешний предметный мир. На втором этапе внешнепредметные действия превращаются во внутренние. Рождается интеллектуальная деятельность, которая есть уже оперирование не с реальными объективными предметами, а с их умственными репрезентациями. Этот этап может быть представлен как процесс превращения формы деятельности в форму предмета, существующего не в виде материального объекта, а в виде образа, помеченного знаком. Третий этап характерен для вербального и синтетического мышления

Процесс обучения математике, построенный на основе когнитивно-визуального подхода к формированию знаний, умений и навыков (идею выдвинул В.А. Далингер

Практика показывает, что обеспечить осознанное изучение абстрактных математических понятий, опираясь исключительно на логические компоненты мышления студентов, затруднительно. Когнитивно-визуальный подход снимает акцент с логического компонента мышления, что способствует сбалансированной активности головного мозга за счет разумного сочетания логических и образных компонентов мышления. В процессе изучения математики у студентов возникают образы на различных этапах познания. Поэтому важна опора на образный компонент мышления, который позволяет использовать разнообразные формы представления математических понятий.

Суть когнитивно-визуального подхода к обучению математике отражают следующие положения

1. Наглядность содержания идей, лежащих в основе абстрактных математических понятий, возможности их выражения в различных для восприятия формах, можно свести к совокупности визуальных образов, что позволяет задействовать резервы визуального мышления для усвоения этих понятий.

2. Визуальная информация обладает уникальным свойством, позволяющим через ее специальную организацию и оформление естественным путем влиять на различные стороны мышления, в том числе и на абстрактную (логическую). Правильная реализация этого свойства предполагает создание условий, при которых значение понятий, на основе которых генерируется информация, становятся легко воспринимаемыми, считываемыми и наглядными.

3. Современные методы визуализации данных и визуальные техники значительно повышают уровень понимания и интерпретации математических понятий и процессов, участвуют в разработке метакогнитивных стратегий, что помогает организовать мысли и увидеть связи между различными концепциями.

Реализация когнитивно-визуального подхода в процессе обучения математике позволяет сконструировать когнитивно-визуальную учебную среду – совокупность условий обучения, в которых акцент ставится на использование резервов визуального мышления обучающегося. Эти условия предполагают наличие, как традиционных наглядных средств, так и специальных средств и приемов, позволяющих активизировать работу зрения

Когнитивно-визуальная учебная среда способствует формированию математической компетентности студентов колледжа, облегчая восприятие и понимание изучаемых математических понятий и их приложений. Использование графиков, схем, анимации и интерактивных моделей позволяет сделать процесс обучения более наглядным, интуитивно понятным и эффективным.

Для эффективного обучения математике в когнитивно-визуальной учебной среде необходимо учитывать ряд принципов.

Принцип когнитивной визуализации – математические объекты должны быть представлены в виде, который облегчает их восприятие и анализ (графики, диаграммы, интерактивные модели).

Принцип динамической визуализации – использование анимации и интерактивных элементов позволяет прослеживать изменения математических зависимостей в реальном времени.

Принцип интеграции профессионально-ориентированного контекста – визуальные модели должны быть связаны с профессиональными задачами, что делает обучение более прикладным.

Принцип интерактивности – использование цифровых инструментов, позволяющих студентам самостоятельно изменять параметры моделей и наблюдать за изменениями.

Современные технологии усиливают возможности для визуального представления информации. Среди наиболее значимых инструментов можно выделить:

– Системы компьютерной графики и моделирования (GeoGebra, MATLAB, AutoCAD) – позволяют строить интерактивные математические модели, работать с трехмерными объектами и анализировать сложные зависимости.

– Дополненная и виртуальная реальность (AR/VR) – создают эффект присутствия, обеспечивают глубокое погружение в учебный процесс и позволяют изучать объекты, недоступные в реальной среде.

– Адаптивные образовательные платформы (Moodle, Coursera, Khan Academy) – обеспечивают персонализированное обучение, используя методы визуализации для представления учебного материала в наиболее удобной форме.

Проверка эффективности предлагаемой методики обучения математике, построенной на основе когнитивно-визуального подхода, осуществлялась в рамках экспериментального обучения.

Эксперимент проводился на I, II курсах Колледжа Университета «Синергия» (Омск, 2023-2025 гг.) Для контроля результатов использовались специально разработанные варианты контрольных заданий. Эксперимент проводился по следующей схеме: первичный контроль (установочная контрольная работа – начало 2023/2024 учебного года) и вторичный контроль (итоговая контрольная работа – зимняя сессия 2024/2025 учебного года). В эксперименте участвовало 60 обучающихся.

Обучение в экспериментальных группах велось по экспериментальной методике, основные положения которой отражены в исследовании. Дополнительного времени на изучение математике, в частности элементов математического анализа не выделялось, различия касались лишь переструктурирования материала и изменения подхода к обучению понятиям функции, непрерывности и предела функции, производной и интеграла; в экспериментальной группе применялись различные визуальные средства, методы и техники.

Фрагментарно опишем применяемые в обучении экспериментальной группы методы визуализации, демонстрирующие авторскую методику:

1. Графическое представление функций и уравнений – построение графиков в программах (например, GeoGebra, Desmos) помогает студентам анализировать зависимости между переменными.

2. Интерактивные модели – использование математических симуляторов (Wolfram Alpha, MATLAB) для визуального анализа сложных математических процессов.

3. Дополненная и виртуальная реальность – технологии AR/VR позволяют работать с трехмерными объектами, что особенно полезно при изучении аналитической геометрии и линейной алгебры.

4. Геймификация и визуальные задачи.

Приведем пример визуальной задачи по интегральному исчислению.

Задача. Доказать неравенство: , не прибегая к непосредственному вычислению интеграла.

Без наглядных иллюстраций обучающийся эту задачу не решит. Все упрощается если сделать чертеж (рис. 1) и воспользоваться геометрическим смыслом интеграла.

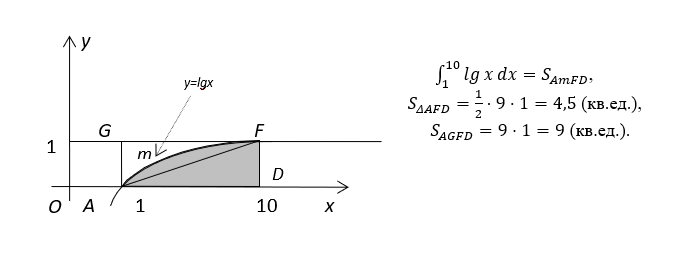
Рисунок 1 - Чертеж к задаче

DOI:10.60797/IRJ.2025.153.23.1

Наглядность позволяет утверждать, что , откуда имеем .

После проведения эксперимента из совокупностей обучающихся были составлены две случайные выборки. Объем каждой выборки – 20 обучающихся. Для сравнения результатов были построены гистограммы по данным вторичного тестирования обеих групп (рис. 2).

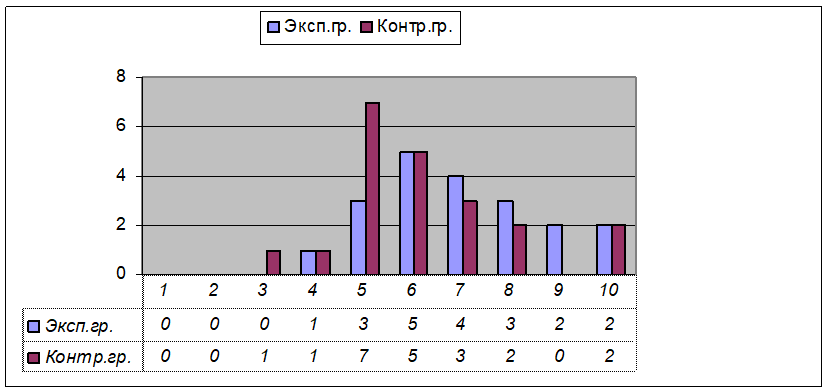
Рисунок 2 - Результаты вторичного тестирования экспериментальной и контрольной групп

DOI:10.60797/IRJ.2025.153.23.2

Анализ результатов экспериментального обучения позволяет сделать вывод о том, что методика, применяемая в экспериментальной группе, оказалась эффективнее, так как гистограмма вторичного контроля экспериментальной группы сдвинута вправо (в область высоких баллов) относительно соответствующей гистограммы, построенной для контрольной группы.

Отметим, что авторской группой был проведен многоаспектный контроль эффективности предложенных педагогических воздействий, осуществленный с применением методов математической статистики, который подтвердил эффективность разработанной методики обучения началам математического анализа студентов колледжа, построенной на основе когнитивно-визуального подхода.

Реализация когнитивно-визуального подхода к обучению математике способствует повышению эффективности учебного процесса, усилению развивающей функции математики и формированию математической компетентности студентов колледжа, которая определяет способность осмысленно и эффективно использовать математические знания, умения и навыки в различных контекстах.

В заключение определим пути реализации когнитивно-визуального подхода к обучению студентов колледжа математике, которые сводятся к следующему:

– учет специфики и особенностей визуального мышления при усвоении материала курса математики, которые состоят в том, что визуальное мышление выступает как деятельность по перекодированию образов, создаваемых на основе разных по типу и форме наглядных изображений;

– активное и целенаправленное использование познавательной функции наглядности;

– использование визуального языка (языка образов) как основного средства, позволяющего оперировать с математическими понятиями по правилам и в соответствии с методами и приемами визуального мышления;

– создание когнитивно-визуальной среды обучения;

– акцентное проектирование учебной наглядности;

– использование возможностей информационных технологий и цифровой образовательной среды в качестве мощных средств организации наглядности.