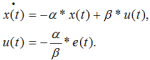СИНТЕЗ ОПТИМАЛЬНЫХ УПРАВЛЕНИЙ ДЛЯ ЗАДАННЫХ ОБЪЕКТОВ
Прохорова О.В.
Доктор технических наук, доцент, Самарский архитектурно - строительный университет.
СИНТЕЗ ОПТИМАЛЬНЫХ УПРАВЛЕНИЙ ДЛЯ ЗАДАННЫХ ОБЪЕКТОВ
Аннотация
В статье рассматриваются два подхода к решению задач оптимального управления: на основе решения уравнения Риккати и на основе моделирования процессов в комплексной области. На примере одного объекта выполнен поиск оптимальных управлений и показаны сильные и слабые стороны рассматриваемых подходов.
Ключевые слова: оптимальное управление, уравнение Риккати, система автоматического регулирования, передаточная функция, характеристическое уравнение.
Prokhorova O.V.
Dr.Sci.Tech, docent, Samara state university of architecture and civil engineering.
SYNTHESIS OF OPTIMAL CONTROLS FOR GIVEN OBJECTS
Abstract
The article describes two approaches of the optimal control tasks solution. First of that is based on the solution of the Rikkati equation. Second one is based on the processes modelling in the complex field. The optimal control by two methods was determined for the one object. Powerful and inefficient sides of both approaches were shown.
Keywords: optimal control, Rikkati’s equation, automatic control system, transfer function, characteristic equation.
Рассмотрим объект управления, возмущенное движение которого, описывается в первом приближении уравнением [1]:
\[\overset{{}}{\mathop{\overset{\bullet }{\mathop{x(t)}}\,=A*x(t)+B*u(t),}}\,\begin{matrix}
{} & {} \\
\end{matrix}\begin{matrix}
x({{t}_{0}})={{x}^{(0)}},{{t}_{0}}=0. & {} \\
\end{matrix}\]
(1)
Здесь А и В – заданные матрицы чисел размеров n×n и n×m соответственно; x(t) – вектор состояния (вектор фазовых координат) размерности n×1; u(t) – вектор управления размерности m×1. Рассмотрим критерий:
\[J=\int\limits_{0}^{\infty }{[{{x}^{T}}(t)*{{R}_{1}}*x(t)}+{{u}^{T}}(t)*{{R}_{2}}*u(t)]dt.\]
(2)
где R1 и R2 – положительно определенные симметрические матрицы размеров n × n и m × m соответственно. Тогда задача определения u(t), t0 ≤ t ≤ ∞ , при котором критерий минимален, называется задачей детерминированного линейного оптимального управления для регулятора с постоянными параметрами.
Закон управления определяется соотношениями:
\[u(t)=-F*x(t)\], \[F=-R_{2}^{-1}*{{B}^{T}}*P\]
(3)
Установившееся решение Р является решением алгебраического уравнения Риккати:
\[0={{R}_{1}}-P*B*R_{2}^{-1}*{{B}^{T}}*P+{{A}^{T}}*P+P*A\]
(4)
Пусть объект состоит из двигателя постоянного тока, управляемого входным напряжением μ(t) с угловой скоростью вала ξ(t). Система описывается скалярным дифференциальным уравнением состояния [2]:Рассмотрим применение выше изложенного для решения задачи стабилизации угловой скорости.
(5)
В качестве критерия оптимальности будем рассматривать критерий вида:
\[J=\int\limits_{{{t}_{0}}}^{\infty }{[{{x}^{T}}(t)*1*x(t)+\rho *{{\mu }^{2}}(t)]dt}\]
(6)
Проведем параллель в обозначениях (1) – (6) и (5) – (6), получим:
x(t) = ξ(t); u(t) = μ(t) ; A = -α; B = ; R1 = 1; R2 = ρ.
Подставим (7) в (4), получим:
\[0=1-\frac{{{\beta }^{2}}}{\rho }*{{P}^{2}}-2\alpha *P\]
(8)
Из (8) определим Р, как корень квадратного уравнения. Будем иметь:
\[{{P}_{1,2}}=\frac{\rho }{{{\beta }^{2}}}\left( -\alpha \pm \sqrt{{{\alpha }^{2}}+\frac{{{\beta }^{2}}}{\rho }} \right)\]
(9)
Для дальнейших расчетов возьмем один из корней:
\[P=\frac{\rho }{{{\beta }^{2}}}\left( -\alpha +\sqrt{{{\alpha }^{2}}+\frac{{{\beta }^{2}}}{\rho }} \right)\]
Определим матрицу F из (3). Будем иметь:
\[F=-\frac{1}{\rho }\beta *\frac{\rho }{{{\beta }^{2}}}\left( -\alpha +\sqrt{{{\alpha }^{2}}+\frac{{{\beta }^{2}}}{\rho }} \right)\]
(10)
или
\[F=-\frac{1}{\beta }\left( -\alpha +\sqrt{{{\alpha }^{2}}+\frac{{{\beta }^{2}}}{\rho }} \right).\]
(11)
Таким образом,\[\mu (t)=-F*\xi (t)=\frac{1}{\beta }\left( -\alpha +\sqrt{{{\alpha }^{2}}+\frac{{{\beta }^{2}}}{\rho }} \right)*\xi (t).\]
(12)
Подставим (12), (11) в (5). Будем иметь:\[\overset{\bullet }{\mathop{\xi (t)}}\,=-\alpha *\xi (t)+\beta *\frac{1}{\beta }\left( \alpha -\sqrt{{{\alpha }^{2}}+\frac{{{\beta }^{2}}}{\rho }} \right)*\xi (t)\] или
\[\overset{\bullet }{\mathop{\xi }}\,(t)=-2*\sqrt{{{\alpha }^{2}}+\frac{{{\beta }^{2}}}{\rho }}*\xi (t).\]
(13)
Система, поведение которой описывается уравнением (13), является асимптотически устойчивой, т.к. получена с учетом минимума функционала (2).
Рассмотрим другую методику решения задачи синтеза оптимального управления для заданного объекта на основе моделирования процессов в комплексной области, предложенную автором [3] и сравним оба подхода между собой. Запишем уравнения (5), (12) в стандартном виде:
(14)
где g(t) – задающее воздействие для управляемого параметра. Обозначим разность g(t) – x(t) через е(t), что представляет собой ошибку в работе устройства, которую необходимо компенсировать вырабатываемым управляющим воздействием. Применим к функциям преобразование Лапласа, получим:(15)
Из первого уравнения выразим X(s). Будем иметь:
\[\overset{{}}{\mathop{X(s)}}\,=\frac{\beta *U(s)}{s+\alpha }.\]
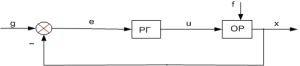
Представим схему системы автоматического регулирования (САР) в виде:
Рис. 1 -Структурная схема САР
Передаточная функция объекта регулирования имеет вид:
\[\overset{OP}{\mathop{W(s)}}\,=\frac{\beta }{s+\alpha }.\]
В качестве регулятора возьмем безынерционное звено с передаточной функцией:
\[\overset{}{\mathop{W(s)}}\,={{k}_{1}}.\]
Задача синтеза стабилизирующего управления предполагает определение значения k1, при котором выполняется первая теорема Ляпунова. На этом и будет строиться решение. Для этого найдем передаточную функцию САР, получим:
\[\overset{}{\mathop{W_{g-x}^{{}}(s)}}\,={{k}_{1}}*\frac{\beta }{s+\alpha }:\left[ 1+\frac{{{k}_{1}}*\beta }{s+\alpha } \right]=\frac{{{k}_{1}}*\beta }{s+\alpha +{{k}_{1}}*\beta }.\]
Для асимптотической устойчивости САР необходимо, чтобы корень характеристического уравнения:
\[s+\alpha +{{k}_{1}}*\beta =0\begin{matrix}
{} & {} \\
\end{matrix}\]
был отрицательным. Это выполнимо, если
\[\alpha +{{k}_{1}}*\beta >0,\begin{matrix}
{} & {} \\
\end{matrix}{{k}_{1}}>-\frac{\alpha }{\beta },\begin{matrix}
{} & {} \\
\end{matrix}\alpha ,\beta >0.\begin{matrix}
{} & \alpha ,\beta -const. \\
\end{matrix}\]
(16)
Поскольку по характеристическому уравнению уже было принято решение для обеспечения устойчивости САР воспользуемся им и подставим вместо k1 величину \[-\frac{\alpha }{\beta }\] в U(t), будем иметь:
\[U(t)=-{{k}_{1}}*e(t)=-\frac{\alpha }{\beta }*e(t).\]
(17)
Подставим (17) в (15), получим:
(18)
Откуда следует, что для стабилизации управления заданным объектом достаточно, применив схему управления (Рис.1) с регулятором в виде безынерционного звена с коэффициентом передачи k1, обеспечивать уравнение динамики вида:\[\overset{\bullet }{\mathop{x(t)}}\,=-\alpha *x(t)-\alpha *e(t)=-\alpha *(2*x(t)-g(t)).\]
(19)
Система, поведение которой описывается уравнением (19), является асимптотически устойчивой, т.к. уравнение получено с учетом выводов первой теоремы Ляпунова. Сравнение результатов двух независимых методик синтеза оптимального управления на данном примере показало, что методика на основе моделирования процессов в s - области не требует алгебраических операций с матрицами и векторами, что является трудоемким процессом, кроме того расчеты выглядят наглядными и простыми.
Литература
- Файзрахманов Р.А., Липатов И.Н. Методические указания к практическим занятиям по курсу «Теоретические основы автоматизированного управления». Пермь : Перм. гос. ун-т, 2006.
- Афанасьев В.Н., Колмановский В.В., Носов В.Р. Математическая теория конструирования систем управления. М.: Высшая школа, 1989, с. 388-393.
- Прохорова О.В. Оптимизация и синтез многомерных САУ на основе моделирования процессов в s – области. Монография. - М.: АПКиППРО, 2010.– 158 с.
References
- Fajzrahmanov R.A., Lipatov I.N. Metodicheskie ukazanija k prakticheskim zanjatijam po kursu «Teoreticheskie osnovy avtomatizirovannogo upravlenija». Perm' : Perm. gos. un-t, 2006.
- Afanas'ev V.N., Kolmanovskij V.V., Nosov V.R. Matematicheskaja teorija konstruirovanija sistem upravlenija. M.: Vysshaja shkola, 1989, s. 388-393.
- Prohorova O.V. Optimizacija i sintez mnogomernyh SAU na osnove modelirovanija processov v s – oblasti. Monografija. - M.: APKiPPRO, 2010.– 158 s.