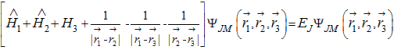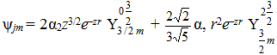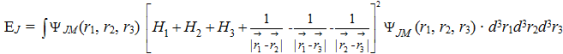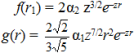РАСЩЕПЛЕНИЕ ОСНОВНОГО СОСТОЯНИЯ ЭКСИТОНА, СВЯЗАННОГО НА НЕЙТРАЛЬНОМ АКЦЕПТОРЕ
Латухин А.Ю.1, Лобаев А.Н.2, Якунин Ю.И.3
1Кандидат технических наук, доцент; 2кандидат физико-математических наук, доцент; 3кандидат физико-математических наук, доцент, Нижегородский государственный технический университет им. Р.Е.Алексеева
РАСЩЕПЛЕНИЕ ОСНОВНОГО СОСТОЯНИЯ ЭКСИТОНА, СВЯЗАННОГО НА НЕЙТРАЛЬНОМ АКЦЕПТОРЕ
Аннотация
В рамках приближения эффективной массы, вариационным методом вычислена энергия связи экситона на нейтральном акцепторе для разных значений полного момента J. Обсуждается величина расщепления энергии основного состояния обусловленная j-j связью и принципом Паули.
Ключевые слова: Экситонно-примесные комплексы, энергия связи, приближение эффективных масс, сферическое приближение, численное моделирование.
Latuhin A.Yu.1,Lobaev A.N.2,Yakunin Yu.I.3
1Candidate of Sciences in Technics, 2Candidate of Physico-mathematical Sciences, assistant professor, 3Candidate of Physico-mathematical Sciences, assistant professor, Nizhny Novgorod State Technical University n.a. R.E. Alekseev.
SPLITTING OF THE GROUND STATE OF AN EXCITON ASSOCIATE WITH NEUTRAL ACCEPTOR
Abstract
The binding energy of exciton in the neutral acceptor for different values of the total angular momentum J within the effective mass approximation is calculated by variational method. The value of the ground state energy splitting due jj coupling and the Pauli principle is discussed.
Key words: Exciton-impurity complexes, binding energy, effective mass approximation, spherical approximation, numerical simulation
Изучение оптических свойств полупроводников при больших уровнях возбуждения носителей заряда, привело к пониманию того, что в полупроводниках могут существовать достаточно экзотические системы, которые называются многочастичными экситон-примесными комплексами [1].
Экситон-примесные комплексы, похожи на атомы, стой лишь разницей, что в них есть как электронные так и дырочные оболочки. Так же существенным отличием их от атомов является более глубокое вырождение дырочных уровней, за счет зонной структуры полупроводников.
В настоящей заметке мы рассмотрим расщепление основного состояния экситона, связанного на нейтральном акцепторе (A0X1). Основному состоянию комплекса A0X1 с полным моментом J соответствует состояние дырок с проекциями момента jz ± 3/2 и электрона с проекцией спина sz = ½. Энергия основного состояния A0X1 различна для различных J. Учитывая j-j связь и принцип Паули, можно показать, что при сложении моментов дырок расщеплены состояния с J=0, 2. Величина энергии основного состояния экситона, связанного на нейтральном акцепторе, существенным образом зависит от зонной структуры полупроводников и типа примеси, на которой связан экситон (глубокая или мелкая). Так как обменное расщепление дырочных состояний не зависит от типа примеси, то значительный интерес представляет определение расщепления основного состояния ∆ комплекса A0X1
∆E20 = E0 – E2. (1)
Последовательный учет зонной структуры делает расчет энергии основного состояния затруднительным, поэтому ограничимся рассмотрением задачи в сферическом приближении [2], пренебрегая анизотропией и гофрировкой валентной зоны. Тогда уравнения Шредингера для A0X1 в приближении эффективных масс примет вид
где – ![]() радиус вектор дырки (i = 1, 2), а
радиус вектор дырки (i = 1, 2), а ![]() – радиус вектор электрона.
– радиус вектор электрона.
Hi (i = 1, 2) – гамильтониан однократного акцептора [3].
Здесь Ji, mi – полный момент и его проекция на ось z (i-той) дырки, – вектор матриц Паули, λ – спин-орбитальное расцепление, а σ и – определяются соотношениями
где me – эффективная масса электрона, а Mh и mh – эффективные массы тяжелой и легкой дырок. Кроме того мы пользуемся кулоновской системой единиц
e – заряд электрона, x – статическая диэлектрическая проницаемость, ħ – постоянная Планка.
Учитывая, как указано выше, j-j связь и считая λ >> |Eji|, ji = 3/2 выберем пробную функцию ΨJM (r1, r2, r3) в виде
ΨJM (r1, r2, r3) = ФJM (r1, r2) φ(r3), (7)
где φ(r3) имеет вид
а ФJM (r1, r2), используя правила векторного сложения [3] записывается как
где ![]() – коэффициенты Клебша-Годана [4].
– коэффициенты Клебша-Годана [4].
Решение ![]() для акцепторов искалось в виде разложения по шаровым векторам
для акцепторов искалось в виде разложения по шаровым векторам ![]() , для J = j = 2/3
, для J = j = 2/3
где α1, α2, z – вариационные параметры, причем α12 + α22 = 1, вследствие нормировки ψjm.
Энергия основного состояния Ej определяется следующим выражением
Выражение (10) после интегрирования по ![]() минимизировалось по α1, α2, x, z для полных моментов J = 0 и J = 2.
минимизировалось по α1, α2, x, z для полных моментов J = 0 и J = 2.
Численные расчеты показывают, что энергетический терм с J = 2 лежит по энергии ниже, чем энергетический терм с J = 0, что согласуется с правилом Хунда для сложных атомов. Этот факт является нетривиальным, так как в отличие от сложных атомов экситонно-примесный комплекс состоит из двух сортов частиц с разным знаком заряда. Выражение (10) позволяет определить по формуле (1) обменное расщепление основного состояния A0X1
здесь r< min(r1, r2), r> = max(r1, r2)
Значения ∆E20 для полупроводников структуры алмаза и цинковой обманки приведены в таблице 1.
Как видно из таблицы величины ΔE20 для большинства рассматриваемых полупроводников находятся в хорошем согласии с экспериментом. Однако, в некоторых случаях экспериментальное значение ∆E20 становится отрицательным, что говорит о том, терм E0 находится по энергии ниже терма E2. Данное обстоятельство, по-видимому связано с влиянием внутрикристаллического поля на комплекс A0X1, что не учитывалось в расчетах.
Таблица 1 - Значения энергии jj расщепления ΔE20 основного состояния экситона, локализованного на нейтральном акцепторе.
Литература
- Брандт Н. Б., Кульбачинский В.А. Квазичастицы в физике конденсированного состояния.−М.:Физматлит, 2005. 631 с.
- Келдыш Л.В. Глубокие уровни в полупроводниках // ЖЭТФ. 1963. Т. 45. №2. С.364-365.
- Ахиезер А. И., Берестецкий В. Б. Квантовая электродинамика. – М.: Наука, 1969. 623 с.
- Бир Г.Л., Пикус Г.Е. Симметрия и деформационные эффекты в полупроводниках. – М.: Наука, 1972. 584 с.
- Venghaus H., Dean P.J. Shallow-acceptor, donor, free-exciton and bound exciton states in high-purity zinc telluride // Phys. Rev. B .1980. V.21. N 4. P.1596-1609.
- Thewalt M.L.V. Fine structure of the luminescence from exciton and multiexciton complexes bound to acceptors in Si //Phys. Rev. Lett. .1977. V.38. N. 9. P521-524.
References
- Brandt N. B., Kul'bachinskij V.A. Kvazichasticy v fizike kondensirovannogo sostojanija.−M.:Fizmatlit, 2005. 631 s.
- Keldysh L.V. Glubokie urovni v poluprovodnikah // ZhJeTF. 1963. T. 45. №2. S.364-365.
- Ahiezer A. I., Beresteckij V. B. Kvantovaja jelektrodinamika. – M.: Nauka, 1969. 623 s.
- Bir G.L., Pikus G.E. Simmetrija i deformacionnye jeffekty v poluprovodnikah. – M.: Nauka, 1972. 584 s.
- Venghaus H., Dean P.J. Shallow-acceptor, donor, free-exciton and bound exciton states in high-purity zinc telluride // Phys. Rev. B .1980. V.21. N 4. P.1596-1609.
- Thewalt M.L.V. Fine structure of the luminescence from exciton and multiexciton complexes bound to acceptors in Si //Phys. Rev. Lett. .1977. V.38. N. 9. P521-524.