Алгоритм ускоренной томографической итерационной реконструкции для ограниченных данных с использованием фильтрации синограммы и регуляризации L0 нормой градиента
Алгоритм ускоренной томографической итерационной реконструкции для ограниченных данных с использованием фильтрации синограммы и регуляризации L0 нормой градиента
Аннотация
Основным методом томографической реконструкции является метод обратного проецирования фильтрованных проекций с использованием быстрого преобразования Фурье, а его альтернативой является использование итерационных алгебраических методов, которые дают возможность использования априорных данных. В данной работе предложен итеративный алгоритм томографической реконструкции с обратным проецированием фильтрованных проекций и регуляризацией на основе сглаживания изображения посредством минимизации L0 нормы градиента. Рассмотренный алгоритм был протестирован в среде MATLAB применительно к реконструкции цифровых фантомов в веерно-лучевой 2D-геометрии сканирования. Результаты численного моделирования с использованием графического процессора показали возможность решения задач томографии с ограниченными данными за приемлемое время. Показана возможность использования быстрых сглаживающих фильтров для обработки видеоконтента в разработке эффективных алгоритмов томографической реконструкции на различных программных платформах.
1. Введение
Основным методом томографической реконструкции является метод обратного проецирования фильтрованных проекций с использованием быстрого преобразования Фурье
, . Основным недостатком этого метода является появление артефактов, возникающих при использовании ограниченного набора данных при съемке объектов в ограниченном угловом диапазоне или при съемке с большим угловым шагом сканирования. Необходимость съемки и реконструкции с ограниченным набором данных возникает из-за ограничений по углам съемки для больших планарных объектов при ламинографии , или при медицинских исследованиях объектов с ограниченным набором проекций с целью снижения лучевой нагрузки.Альтернативой реконструкции методом обратного проецирования является использование итерационных алгебраических методов
, которые дают возможность использования априорных данных , . Для реконструкции объектов, составленных из однородных по химическому составу и плотности компонентов, предпочтительно применять алгоритмы, основанные на минимизации L1 и L0 норм градиента плотности, которые дают большую скорость сходимости и минимальные артефакты при ограниченных данных , , , . Недостатком алгебраических методов является большие вычислительные затраты и низкая скорость сходимости при плохой обусловленности проекционных матриц.2. Новизна работы
Метод сглаживания изображений, основанный на минимизации L0 градиента, был опубликован в 2011 г. в работе
. Метод осуществляет сохранение и усиление важных границ, задаваемых параметром сглаживающей функции, при этом устраняя незначительные вариации изображения, которые ниже установленного порога. Устранение артефактов пороговым сглаживанием изображения непосредственно в процессе реконструкции, было предложено в работе , в которой L0 норма градиента изображения использовалась в качестве функционала регуляризации. Программный код сглаживающей функции LOSmoothing в MATLAB доступен по актуальной ссылке в вышеупомянутой работе.Предложенная нами фильтрация синограмм в процессе итерации дает возможность усилить края реконструируемого изображения и тем самым делать более эффективным регуляризацию по L0 норме. Другим важным шагом является использование метода моментов, который существенно ускоряет итерационный процесс. В ходе численного моделирования нами также было установлено, что оптимальное убывание величины порога сглаживания в процессе итерации осуществляется по степенному закону.
Используемый нами алгоритм L0 сглаживания характеризуется также высокой скоростью обработки изображений мегапиксельного формата со скоростью в сотни кадров в секунду при использовании графического процессора. Это позволяет применять быстрое послойное сглаживание трехмерного изображения непосредственно в итерационном процессе реконструкции, обеспечивая высокую скорость и качество малоракурсной реконструкции трехмерных объектов.
3. Описание алгоритма
Типичная алгебраическая реконструкция осуществляется последовательным сравнением преобразования Радона текущей реконструкции с синограммой данных. Разница синограмм проецируется обратно в пространство изображений при помощи оператора обратного проецирования. В результате этой операции получается корректирующее изображение, которое с определенным весовым коэффициентом, определяющим шаг итерации, добавляется к текущему изображению (рис. 1).
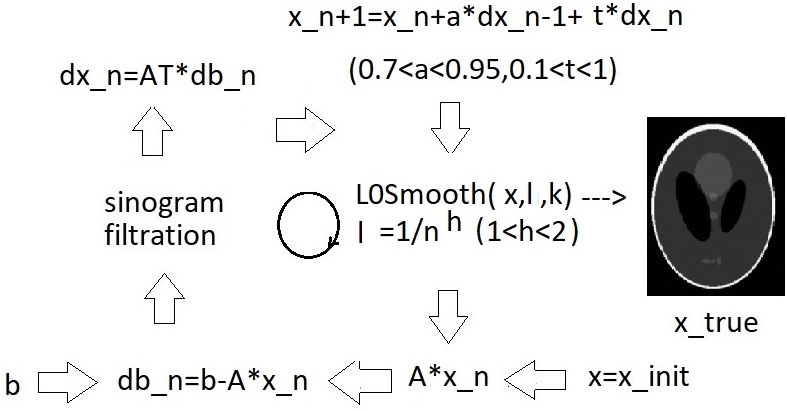
Рисунок 1 - Итерационный цикл ускоренной реконструкции
Чтобы получить однозначное решение в виде точки х_true необходимо либо добавить проекционные данные, которые дают другую гиперплоскость, пересечение которой с исходной дает решение, либо использовать многообразие, составленное из изображений, удовлетворяющих определенным априорным условиям, например, условию кусочной постоянности, которое математически выражается условием минимизации L1 или L0 нормы градиента. Применительно к более сложным объектам определенного типа, например для исследований медицинских и биологических объектов, многообразие дополнительных данных определяется методами сбора статистических данных с явным выделением главных компонент аналитическими методами
или с неявным их выделением с использованием энкодеров или других нейросетевых методов регуляризации .Оператор обратного проецирования AT является оператором, сопряженным к оператору проецирования, и его действие заключается в том, чтобы пошагово проецировать текущую разницу синограмм на ядро оператора проецирования, задаваемое уравнением Ax=0 (рис. 2). Наряду с сопряженным оператором, в алгоритмах SIRT и SART в качестве оператора обратного проецирования используются транспонированные операторы с весовыми коэффициентами.
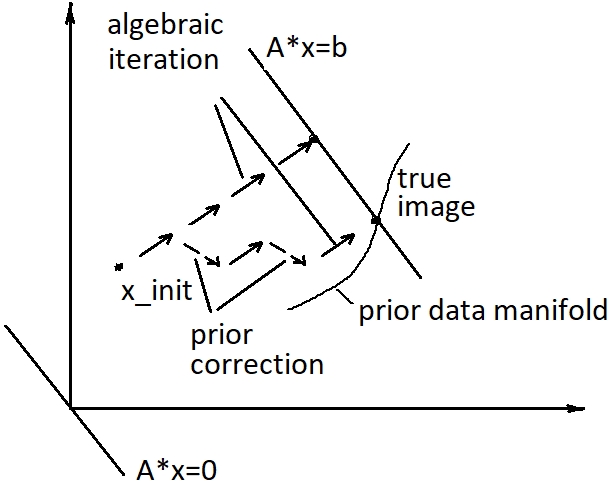
Рисунок 2 - Итерационная последовательность в пространстве изображений
В случае постепенного перехода от параллельного пучка к веерному или конусному или при переходе от полного к разреженному набору данных, резонно ожидать, что фильтрация проекций с обратным проецированием в веерном пучке дает более точное приближение, чем простое обратное проецирование. Поэтому итерационную процедуру можно выполнять с большим шагом и с большей точностью за меньшее число операций (рис. 3).
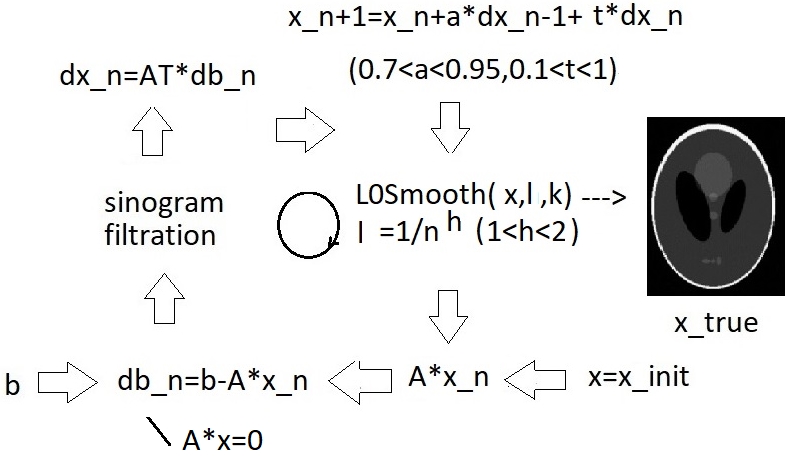
Рисунок 3 - Итерационный цикл ускоренной реконструкции
4. Результаты численного моделирования и их обсуждение
Вышеизложенный алгоритм был протестирован в среде MATLAB (R2023a) применительно к 2D и 3D реконструкции цифровых фантомов в круговой геометрии сканирования веерным и конусным пучками. Численные эксперименты были выполнены на персональном компьютере с процессором Intel Core i7-9700F с рабочей частотой 3 ГГц, оперативной памятью 64 Гб и графическим процессором NVIDIA GeForce 2080 под управлением операционной системы Windows 10.
В первом тесте была промоделирована малоракурсная реконструкция цифрового фантома Форбильда размером 500×500 в веерно-лучевой геометрии при различном числе проекций. Использовались синограммы, полученные для радиального расстояния источник–объект равного 700 мм и веерного пучка с высокой расходимостью в 60° и числом лучей в веерном пучке равном 750, что обеспечивало прохождение каждого пиксела в среднем 1 лучом. Такая экстремальная геометрия была выбрана для обеспечения минимизации эффекта криминальной инверсии, обусловленной пиксельной дискретизацией поля реконструкции. Во втором тесте реконструкция аналогичного фантома производилась для геометрии с ограниченным угловым сканированием, используемой в ламинографии. Разреженная матрица проецирования вычислялась в MATLAB c использованием томографического пакета AIR TOOLs
.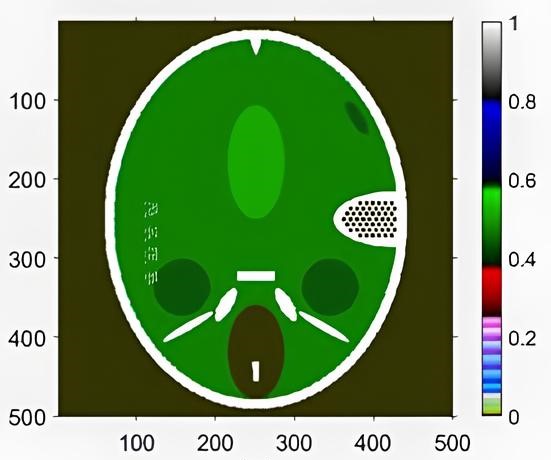
Рисунок 4 - Результаты реконструкции цифрового фантома Форбильда
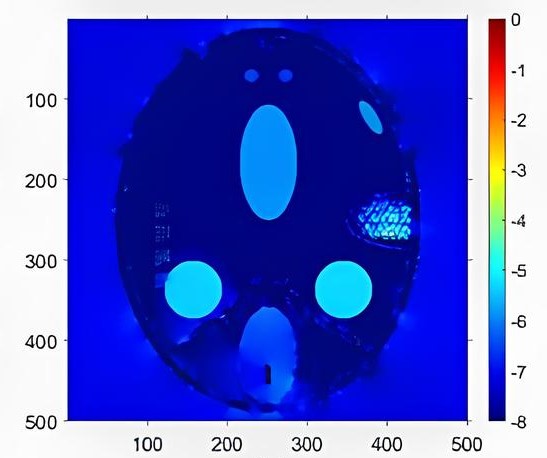
Рисунок 5 - Малоракурсная геометрия c 21 проекциями при шаге сканирования 10º
Примечание: время реконструкции 10 с, число итераций 100
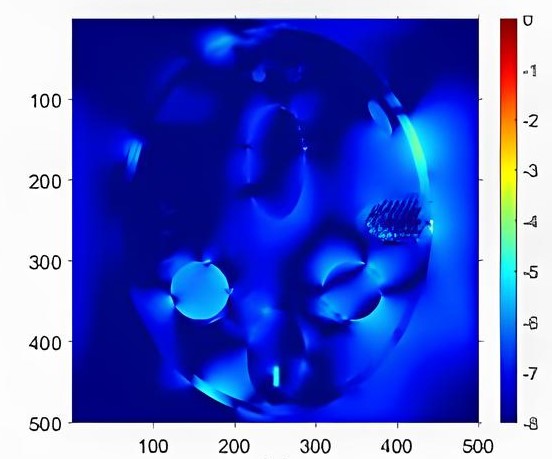
Рисунок 6 - Малоугловая геометрия сканирования c углом 70º
Примечание: время реконструкции 37 с, число итераций 900
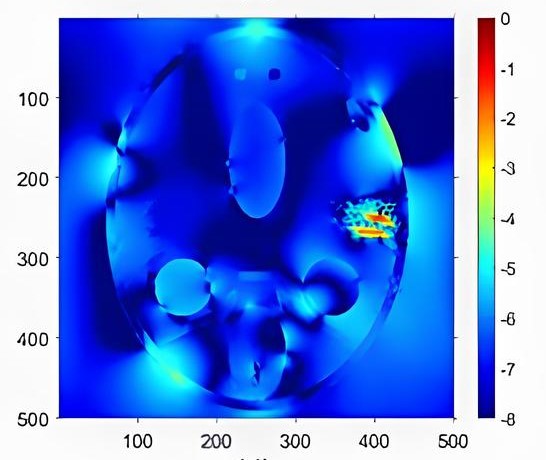
Рисунок 7 - Малоугловая геометрия сканирования c углом 90º
Примечание: время реконструкции 12 с, числе итераций 300
где буквами t и h обозначены векторные представления реконструированного и исходного фантомов длиной N c индексами i.
Более информативным является попиксельное представление точности реконструкции в виде карты разницы объектов (рис. 4-7) с псевдоцветной шкалой в логарифмическом масштабе. Данное представление позволяет оценить качество реконструкции на разных пространственных частотах. Сравнение 2D реконструкций для малоракурсной и малоугловой съемки показывает, что малоракурсная реконструкция точнее малоугловой. Это отражает тот факт, что в первом случае происходит фактически интерполяция изображения объекта в пределах шага углового сканирования, в то время как во втором случае замещение отсутствующих данных вне углового диапазона сканирования происходит за счет экстраполяции.
Для проведения численных экспериментов по 3D реконструкции нами использовался 3D фантом Шепп-Логана и программный модуль реконструкции методом Фельдкампа из томографического пакета TIGER c открытым исходным кодом. В данном пакете прямое и обратное проецирование осуществляется без использования системных матриц посредством параллельной трассировки лучей на графическом процессоре (ГП). Исходный код написан на языке С++ с расширением CUDA и обмен данных между оперативной памятью центрального процессора (ЦП) и памятью ГП организуется в MATLAB через MEX (MATLAB Executable) интерфейс. Непосредственный доступ к памяти ГП в процессе исполнения кода из среды MATLAB был невозможен, поскольку код MATLAB и код, собранный в MEX файле, работают в разных адресных пространствах. Чтобы циклически запускать алгоритм Фельдкампа и затем использовать его результат для сглаживания в среде MATLAB с использованием ГП в другом адресном пространстве, использовался обмен данными между ЦП и ГП, что снизило скорость реконструкции из-за простоя ГП. Вычисления для 3D реконструкции производились с использованием одинарной 32-битной точности. Геометрия численного эксперимента была задана в формате структуры geo из пакета TIGER
(табл. 1, 2).Таблица 1 - Геометрические параметры численного эксперимента
Переменная | Описание | Единицы |
%расстояния | ||
geo.DSD=1536; | источник-детектор | мм |
geo.DSO=1000; | источник-центр вращения | мм |
%параметры детектора | ||
geo.nDetector=[512;512] | число пикселов | |
geo.dDetector=[0,8;0,8]; | размер пиксела | мм |
geo.sDetector=geo.nDetector.*geo.dDetector; | размер кадра изображения | мм |
%параметры изображения | ||
geo.nVoxel=nVoxel=[512;512;512]; | число вокселей | |
geo.dVoxel=[0,5;0,5;0,5]; | размер воксела | мм |
geo.sVoxel=geo.nVoxel.*geo.dVoxel; | размер изображения | мм |
%смещения | ||
geo.offOrigin=[0;0;0]; | смещение изображения от центра вращения | мм |
geo.offDetector=[0;0]; | смещение детектора | мм |
%дополнительные параметры | ||
geo.mode=’cone’; | параллельный или конусный | |
Таблица 2 - Параметры сглаживания
Переменная | Описание |
lambda=1,1/j^1,5 (j – номер томографической итерации) | параметр, контролирующий степень сглаживания |
kappa=27 (2*lambda*kappa^(n-1))<1,e5 | параметр, контролирующий число n ступеней сглаживания |
Угловые положения (для 20 и 40 проекций) были распределены равномерно в интервале от 0 до 220º. На рис. 8, 9 представлены результаты реконструкции 3D фантома для 20 и 40 проекций.
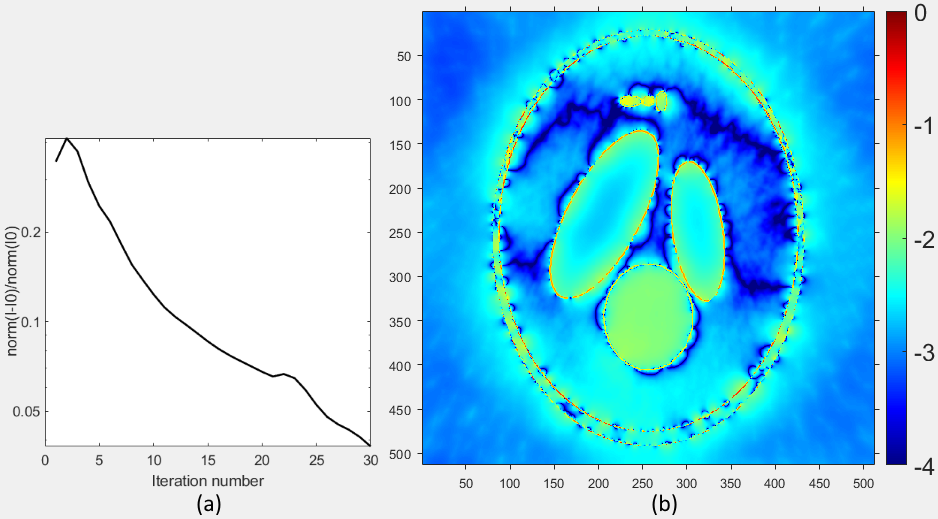
Рисунок 8 - Зависимость нормированной среднеквадратичной ошибки реконструкции от числа итераций (a) и карта ошибки реконструкции в центральном сечении фантома по шкале десятичного логарифма (b)
Примечание: время реконструкции 252 с, число проекций 40
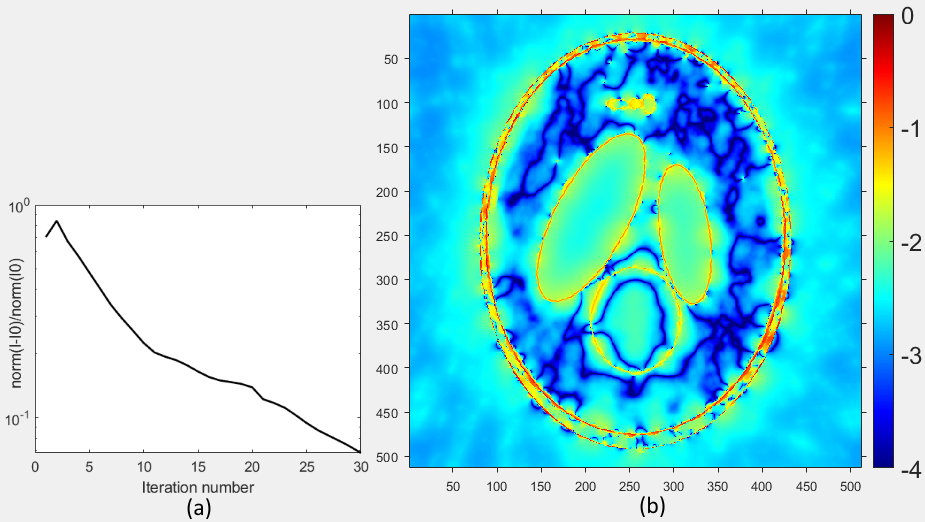
Рисунок 9 - Зависимость нормированной среднеквадратичной ошибки реконструкции от числа итераций (a) и карта ошибки реконструкции в центральном сечении фантома по шкале десятичного логарифма (b)
Примечание: время реконструкции 244 с, число проекций 20
Для референсной оценки качества и скорости реконструкции нашим алгоритмом была произведена реконструкция фантома с аналогичными параметрами съемки методом ASD-POCS, реализованном в пакете TIGER (рис. 10). В алгоритме ASD-POCS с использованием графического процессора осуществляются шаги алгебраической реконструкции со сглаживанием изображений TV нормой. Среди алгоритмов реконструкции, представленных в пакете TIGER, реконструкция с использованием TV нормы оптимальна для решения задач малоракурсной томографии
.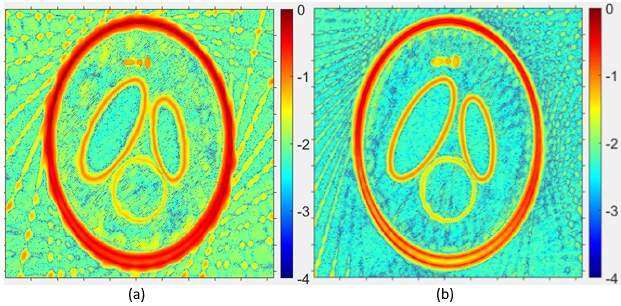
Рисунок 7 - Карта ошибки реконструкции алгоритмом ASD-POCS для 20 (a) и 40 (b) проекций. Число итераций 40, время реконструкции 547 и 1042 с, параметры реконструкции взяты из пакета TIGER по умолчанию
5. Заключение
Полученные нами результаты показывают, что малоракурсная реконструкция объектов в формате 512x512x512 может осуществляться за разумное время в несколько минут, а также в формате 1500x1500x50 применима для многослойных планарных объектов, например печатных плат. По данным работы
дальнейшее уменьшение времени реконструкции может быть достигнуто за счет специального алгоритма прямого и обратного проецирования, примененного в работе и используемого в пакете ASTRA-toolbox с открытым исходным кодом . По сравнению с программным решением, используемым в пакете TIGER, в пакете ASTRA-toolbox время проецирования может быть уменьшено в 2,4 раза. Соответственно, предполагается уменьшить время начальной реконструкции с медианным фильтром. На примере предложенного алгоритма показана возможность использования быстрых сглаживающих фильтров для обработки видеоконтента в разработке эффективных алгоритмов томографической реконструкции на различных программных платформах.