ОПРЕДЕЛЕНИЕ ОБЛАСТИ РАБОТОСПОСОБНОСТИ НА ОСНОВЕ АЛГОРИТМА НЕПРЕРЫВНОГО ПОИСКА ЕЕ ГРАНИЧНЫХ ТОЧЕК

Саушев А.В.¹, Широков Н.В.², Давыдов В.С.³, Шерстнев Д.А.⁴

¹Доктор технических наук, ²Кандидат технических наук, ³аспирант, ⁴аспирант, Государственный университет морского и речного флота (ГУМРФ) имени адмирала С.О. Макарова

ОПРЕДЕЛЕНИЕ ОБЛАСТИ РАБОТОСПОСОБНОСТИ НА ОСНОВЕ АЛГОРИТМА НЕПРЕРЫВНОГО ПОИСКА ЕЕ ГРАНИЧНЫХ ТОЧЕК

Аннотация

Рассмотрены способы поиска граничных точек области работоспособности применительно к техническим системам. Изложен метод секущих, предполагающий непрерывную процедуру поиска. Рассмотрен алгоритм, позволяющий расширить сферу применения метода секущих, а также повысить эффективность поиска за счет анализа не всей, а лишь ограниченной части секущей, определяемой самой областью работоспособности. Приведены количественные оценки разработанного алгоритма. Рассмотрены вероятностные характеристики метода секущих и дана оценка области его применения. Результаты исследования подтверждены примерами практической реализации метода применительно к электротехническим системам.

Ключевые слова: область работоспособности, техническая система, метод секущих, вероятностные характеристики.

Saushev A.V.¹, Shyrokov N.V.², Davydov V.S.³, Sherstnev D.A.⁴

¹PhD in Engineering, Admiral Makarov State University of Maritime and Inland Shipping, ²PhD in Engineering, Admiral Makarov State University of Maritime and Inland Shipping, ³Postgraduate Student, Admiral Makarov State University of Maritime and Inland Shipping, ⁴Postgraduate Student, Admiral Makarov State University of Maritime and Inland Shipping

DEFINITION OF THE FIELD OF WORKING CAPACITY ON THE BASIS OF ALGORITHM OF CONTINUOUS SEARCHING OF ITS BORDER POINTS

Abstract

The article considers the ways of finding boundary points of the field of working capacity for technical systems. The secant method is described, assuming a continuous search procedure. An algorithm that allows expanding the sphere of application of the secant method is considered, as well as improving the search efficiency due to the analysis of a limited part of the secant, determined by the field of the working capacity itself. Quantitative estimates of the developed algorithm are given. The probabilistic characteristics of the secant method are considered and the evaluation of the area of its application is given. The results of the study are confirmed by the examples of practical implementation of the method applied to electrical systems.

Keywords: field of working capacity, technical system, secant method, probabilistic characteristics.

Для решения задач параметрического синтеза и контроля состояния большинства технических систем требуется информация о границе области работоспособности системы [1, С. 41], [2], [3]. Для получения такой информации в виде множества граничных точек области работоспособности принципиально можно воспользоваться двумя подходами. Первый из них предполагает дискретный поиск координат граничных точек области работоспособности. Для их определения разработаны сеточные методы, основанные на обходе области работоспособности по ее контуру [4], [5]. Второй подход основан на непрерывном способе поиска граничных точек. Для этой цели разработаны метод 2ⁿ-звезды и метод секущих [6, С. 106]. В обоих случаях возможны два варианта – когда отсутствует математическая зависимость, связывающая выходные переменные Y объекта исследования с варьируемыми (первичными) параметрами X={X₁, X₂, …, X_i, …, X_n}, i=1, 2, …,n, в пространстве которых строится область работоспособности, и когда такая зависимость имеется.

В настоящей статье рассматривается второй подход к решению задачи, устанавливается область его использования, возможные методы и алгоритмы его реализации. Под областью работоспособности понимается множество значений первичных параметров системы, при которых удовлетворяются все заданные требования к ее выходным параметрам. Для электротехнических систем к первичным параметрам относятся сопротивления резисторов, емкости конденсаторов, индуктивности катушек, коэффициенты жесткости упругих связей, моменты инерции, коэффициенты усиления, постоянные времени и т п., а выходными переменными, например, могут быть показатели качества работы системы – коэффициент полезного действия, время переходного процесса и максимальное перерегулирование исследуемой переменной, интегральный критерий качества.

При отсутствии уравнения, связывающего первичные и выходные параметры системы, на практике находит применение метод секущих [6, С. 106].

При использовании этого метода из начала координат в пространстве первичных параметров проводится r (r = 1,2,…) прямых линий. Каждая прямая в пространстве Rⁿ первичных параметров X может быть задана в параметрическом виде:  − r-е численное значение i-го первичного параметра (направляющий коэффициент r−й прямой), τ – множитель . Известный алгоритм, реализующий метод секущих, может быть использован лишь при условии, что область M (является отображением допусковой области пространства выходных переменных системы Y в пространство первичных параметров X) целиком принадлежит области P (определяет допустимые пределы изменения первичных параметров), либо примыкает к грани этой области и расположена относительно нее так, как показано на Рис. 1а. В остальных случаях (Рис. 1б, в) алгоритм неработоспособен.

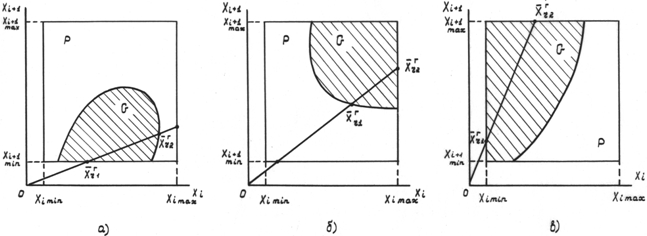
Рис. 1 – Возможные варианты пересечения секущей области работоспособности

 

Рассмотрим алгоритм, устраняющий этот недостаток и предполагающий подсчет числа пересечений области работоспособности r-й секущей. Если их число S равно 2μ, где , т.е. число пересечений равно четному числу, то секущая полностью определяет граничные точки. В том случае, если  (число пересечений равно нечетному числу), происходит фиксация точки, принадлежащей грани области P. Существенным недостатком известного алгоритма является его низкое быстродействие, определяемое двумя причинами. Одной из них является то, что поиск граничных точек каждой секущей продолжается равное число шагов k до тех пор, пока длина отрезка  не достигнет величины l, где Δt – шаг квантования секущей, l – длина наибольшей диагонали области P. Вместе с тем, анализ показывает, что нет необходимости в поиске граничных точек за пределами области P.

  (1)

где t₁ и t₂ – время, затрачиваемое соответственно на проверку заданных условий работоспособности и на переход к следующей исследуемой точке; k₁ и k₂  – число шагов, затрачиваемых соответственно на определение граничных точек согласно известному и рассматриваемому алгоритмам; .

Предположим, что процесс поиска граничных точек носит равновероятный характер, т.е. секущие проводятся равномерно по всему объему области P, параметр α=1, а сама область P имеет форму гиперкуба с ребром, равным h. Данные предположения позволяют оценить нижнюю границу снижения временных затрат. Исходя из принятых предположений и учитывая, что наибольшая диагональ гиперкуба , формула (1) примет следующий вид: . Для двух первичных параметров n=2. При этом , т.е. быстродействие процесса определения границы области работоспособности повышается в 1,17 раза. При . Таким образом, нижняя граница относительного повышения быстродействия рассматриваемого алгоритма по сравнению с известным алгоритмом находится в пределах  при .

Основные достоинства метода секущих имеют место при известной математической зависимости . При этом на эффективность метода существенное влияние оказывает вид функции . Как показано в работе [4, С. 153], достаточно часто вид такой зависимости имеет форму полинома. Пусть n=2 и уравнение  имеет вид   – постоянные коэффициенты. Подставляя значения  в это уравнение и решая его относительно τ, получим уравнение . Решение этого уравнения для предельных значений выходного параметра  , определяет граничные значения .

Рассмотрим вероятностные характеристики поиска граничных точек области работоспособности непрерывными методами. Процесс поиска определяется рядом случайных факторов и может быть принят случайным [7]. К числу таких случайных факторов относятся расположение области работоспособности G относительно области P, ее размер и форма на момент построения границы, способность измерительных приборов фиксировать граничные значения первичных параметров в заданных условиях.

При использовании метода секущих случайным фактором будет также выбор направляющих углов секущей. Пусть в момент времени t проводится секущая α, имеющая направляющие коэффициенты , а в момент времени (t+∆t) – секущая β, имеющая направляющие коэффициенты . Вероятность того, что в момент времени (t+∆t) проводится секущая α, определяется только событием наличия в момент времени t секущей β, и не зависит от того, каким образом были выбраны эти коэффициенты. Поскольку переход от одного направляющего коэффициента к другому осуществляется скачком в любой момент времени, то процесс поиска граничных точек области работоспособности методом секущих можно отнести к марковским процессам с дискретными состояниями и непрерывным временем. Поток обнаружений этого процесса характеризует последовательность пересечений или касаний области работоспособности секущими и является стационарно пуассоновским.

Для определения вероятности P_N(r) того, что из N секущих лишь r из них пересекут или коснутся области работоспособности, введем вероятность g пересечения или касания одной секущей этой области. Эта вероятность g будет равна отношению обозреваемой из начала координат поверхности S_G области работоспособности G к обозреваемой из начала координат поверхности S_P исследуемой допусковой области P, т. е. .

Вероятность P события, что будет зафиксировано пересечение или касание секущей области работоспособности, определяется выражением , где d_u − инструментальная достоверность, определяемая классом точности используемых приборов при проведении натурного эксперимента, служащих для измерения выходных параметров, и точностью фиксаций граничных значений первичных параметров. В соответствии с условиями отсутствия последействия обзор поверхности S_P можно рассматривать как серию из r независимых испытаний. Следовательно, для дальнейшего анализа можно воспользоваться теоремой о повторении опытов, согласно которой вероятность  того, что среди N секущих ровно r секущих пересекут или коснутся области работоспособности G, определяется по формуле , где N – общее число секущих или циклов определения границы области работоспособности.

Вероятность того, что секущая не пересечет или не коснется области работоспособности, определяется по формуле . Вероятность того, что секущие пересекут область работоспособности или коснутся ее хотя бы один раз, равна  [6, С. 123].

Предположим, что время, затрачиваемое на r-й цикл определения граничных точек (время проведения r-й секущей), равно . Тогда для того, чтобы секущие пересекали область работоспособности с вероятностью P_N (r ≥ 1) необходимо выполнить N циклов, на которые потребуется затратить время . При условии, что  получим .

Заметим, что в предложенном алгоритме реальное время   может быть существенно меньше расчетного. Это обусловлено тем, что при обнаружении последней для r-й секущей граничной точки области работоспособности процесс поиска прекращается. Таким образом, для расчетного значения вероятности P_N (r ≥ 1) можно записать , где: ; Т_п − время определения границы области работоспособности. При этом вероятность P_N (r ≥ 1)  определится следующим выражением

       (2)

Полученные формулы позволяют оценить эффективность предложенного алгоритма, реализующего метод секущих. Алгоритм был реализован при решении задач параметрического управления состоянием электротехнических систем на объектах водного транспорта [1], [8], [9], [10]. На его основе разработаны технические устройства, позволяющие автоматизировать процесс поиска граничных точек области работоспособности методом секущих.

Список литературы / References

1. Саушев А. В. Основы управления состоянием электротехнических систем объектов водного транспорта / А. В. Саушев // СПб.: ГУМРФ имени адмирала С. О. Макарова, 2015. – 215 с.
2. Саушев А. В. Метод построения границы области работоспособности электротехнических объектов / А. В. Саушев // Электричество. – 1990. – № 4. – С. 14 – 19.
3. Саушев А. В. Математическое описание областей работоспособности электромеханических систем / А. В. Саушев // Мехатроника, автоматизация, управление. – 2013. – №6(147). – С. 7 – 13.
4. Саушев А. В. Сеточный метод построения областей работоспособности технических объектов на основе алгоритма симплексного поиска / А. В. Саушев // Журнал СПГУВК. ­ 2010. ­ Вып. 1 (5). - С. 58 - 69.
5. Саушев А. В. Построение областей работоспособности технических систем водного транспорта на основе алгоритмов дискретного поиска / А. В. Саушев // Речной транспорт (21 век). ­ 2012. - № 2. ­ С. 69 ­ 74.
6. Саушев, А. В. Области работоспособности электротехнических систем: монография / А. В. Саушев. – СПб.: Политехника, 2013. – 412 с.
7. Саушев А. В. Статистические методы параметрического синтеза электротехнических систем по критерию запаса работоспособности / А. В. Саушев // Журнал СПГУВК. – 2011. – Вып. 4 (12). –С. 49 – 57.
8. Саушев А. В. Методы и алгоритмы параметрического синтеза технических систем на основе областей работоспособности / А. В. Саушев // Международный научно-исследовательский журнал International research journal. – 2016. - № 5 (47), часть 3. – С. 167 – 168.
9. Саушев А. В. Параметрический синтез технических систем на основе линейной аппроксимации области работоспособности / А. В. Саушев // Автометрия. – 2013. – Т.49, № 1. – С. 61–67.
10. Саушев А. В. Диагностирование состояния электротехнических систем в пространстве параметров их элементов / А. В. Саушев, Н. В. Широков // Вестник ГУМРФ им. адм. С.О. Макарова. – 2016. – Вып. 2 (36). –С. 143 – 156.

Список литературы на английском языке / References in English

1. Saushev A. V. Osnovy upravlenija sostojaniem jelektrotehnicheskih sistem ob#ektov vodnogo transporta [Bases of management of a condition of electrotechnical systems of objects of the water transport] / A. V. Saushev // SPb.: GUMRF imeni admirala S. O. Makarova, 2015, ­ 215 P [in Russian]
2. Saushev A. V. Metod postroenija granicy oblasti rabotosposobnosti jelektrotehnicheskih ob#ektov [Method of creation of border of area of operability of electrotechnical objects] / A. V. Saushev // Jelektrichestvo [Electricity]. ­ 1990. ­ № 4. ­.P. 14­19. [in Russian]
3. Saushev A. V. Matematicheskoe opisanie oblastej rabotosposobnosti jelektromehanicheskih sistem [Mathematical description of areas of operability of electromechanical systems] / A. V. Saushev // Mehatronika, avtomatizacija, upravlenie [Mechatronics, automation, management]. ­ 2013. ­ № 6 (147). . ­.P. 7­13. [in Russian]
4. Saushev A. V. Setochnyj metod postroenija oblastej rabotosposobnosti tehnicheskih ob#ektov na osnove algoritma simpleksnogo poiska [A net method of creation of areas of operability of technical objects on the basis of an algorithm of simplex search] / A. V. Saushev // Zhurnal SPGUVK [the SPGUVK Magazine]. ­ 2010. ­ Vyp. 1 (5) ­.P. 58­69. [in Russian]
5. Saushev A. V. ostroenie oblastej rabotosposobnosti tehnicheskih sistem vodnogo transporta na osnove algoritmov diskretnogo poiska [Creation of areas of operability of technical systems of the water transport on the basis of algorithms of discrete search] / A. V. Saushev \\ Rechnoj transport (21 vek) [River transport (the 21st century)]. ­ 2012. ­ № 2. ­.P. 69­74. [in Russian]
6. Saushev, A. V. Oblasti rabotosposobnosti jelektrotehnicheskih sistem / A. V. Saushev. - SPb.: Politehnika, 2013, ­ 412 P [in Russian]
7. Saushev A. V. Statisticheskie metody parametricheskogo sinteza jelektrotehnicheskih sistem po kriteriju zapasa rabotosposobnosti [Statistical methods of parametrical synthesis of electrotechnical systems by criterion of a stock of working capacity] / A. V. Saushev // Zhurnal SPGUVK [the SPGUVK Magazine]. ­ 2011. ­ Vyp. 4 (12). ­.P. 49­57. [in Russian]
8. Saushev A. V. Metody i algoritmy parametricheskogo sinteza tehnicheskih sistem na osnove oblastej rabotosposobnosti [Methods and algorithms of parametrical synthesis of technical systems on the basis of areas of working capacity] / A. V. Saushev // Mezhdunarodnyj nauchno-issledovatel'skij zhurnal [International research journal]. – 2016. - № 5 (47), chast' 3. ­.P. 167­168. [in Russian]
9. Saushev A. V. Parametricheskij sintez tehnicheskih sistem na osnove linejnoj approksimacii oblasti rabotosposobnosti [Parametrical synthesis of technical systems on the basis of linear approximation of area of working capacity] / A. V. Saushev // Avtometrija [Avtometriya]. ­ 2013. ­ T.49, № 1. ­P. 61­67. [in Russian]
10. Saushev A. V. Diagnostirovanie sostojanija jelektrotehnicheskih sistem v prostranstve parametrov ih jelementov [Diagnosing of a condition of electrotechnical systems in space of parameters of their elements] / A. V. Saushev, N. V. Shirokov // Vestnik GUMRF im. adm. S.O. Makarova [the Messenger of GUMRF of atm. S.O. Makarova]. ­ 2016. ­ Vyp. 2 (36). ­ P. 143­156. [in Russian]