ПРОСТОЕ РЕШЕНИЕ ИНТЕРПОЛЯЦИОННОЙ ЗАДАЧИ ЭРМИТА
ORCID: 0000-0002-2465-7475, Кандидат технических наук,
ФГУП Государственный научно-исследовательский институт авиационных систем, Москва
ПРОСТОЕ РЕШЕНИЕ ИНТЕРПОЛЯЦИОННОЙ ЗАДАЧИ ЭРМИТА
Аннотация
Рассмотрена интерполяционная задача Эрмита о построении многочлена, принимающего заданные значения функции и ее производных в узловых точках. Предложен новый способ решения этой задачи. На основе использования формулы Тейлора осуществлено упрощение вывода формулы интерполяционного многочлена Эрмита. Предложена интерпретация этого многочлена в представлениях многочлена Тейлора. Указан алгоритм получения конечных формул для многочлена Эрмита в случаях, когда максимальные порядки производных, заданных в узловых точках, одинаковы.
Ключевые слова: задача Эрмита, многочлен Тейлора, формула для интерполяционного многочлена Эрмита, интерпретация многочлена Эрмита.
Shustov V.V.
ORCID: 0000-0002-2465-7475, PhD in Engineering,
FSUE State Research Institute of Aviation Systems, Moscow
SIMPLE SOLUTION OF HERMIT INTERPOLATION PROBLEM
Abstract
The Hermite interpolation problem on the construction of a polynomial taking given values of a function and its derivatives at the nodal points is considered. A new way of solving this problem is proposed. Using the Taylor formula, we simplified the derivation of the Hermite interpolation polynomial formula. An interpretation of this polynomial in the representations of the Taylor polynomial is proposed. An algorithm is given for obtaining finite formulas for the Hermite polynomial in cases when the maximal orders of the derivatives given at the node points are the same.
Keywords: Hermite problem, Taylor polynomial, the formula for the Hermite interpolation polynomial, interpretation of the Hermite polynomial.
ВведениеИнтерполяционный многочлен Эрмита известен давно [1], [2, С. 163], [3, С. 71], [4, С. 154], [5, С. 143], [6] и используется в теории и практике для различных целей. В частности, он применяется для интерполяции функций, заданных в виде таблиц, в которых заданы значения функции и значения ее производных, и может использоваться для аппроксимации функций, принадлежащих определенному классу гладкости. В этом случае для повышения точности приближения используются данные о значениях функции и ее производных в нескольких точках отрезка.
Данный подход в случае выбора аппроксимирующей функции в классе многочленов приводит к задаче интерполирования Эрмита [2, С. 163-165] и рассмотренной в [1, С. 70-79]. Для решения задачи интерполяции строится многочлен, называемый интерполяционным многочленом Эрмита.
Вывод представления для интерполяционного многочлена Эрмита в общем случае для произвольного числа узловых точек приводится, например, в [2, С. 169-172], [3, С. 71-73], [4, С. 154-155] и является сложным и достаточно объемным. Вывод представления связан с предельными переходами и при некоторых подходах требует использования методов теории функций комплексного переменного.
Сложность вывода общей формулы для многочлена Эрмита побуждает ряд авторов тем или иным путем упростить его. Например, в работе [7] упрощение ищется в рамках линейной алгебры путем обращения матрицы.
Целью настоящей работы является с одной стороны дальнейшее упрощение вывода представления для интерполяционного многочлена Эрмита, с другой стороны разработка способов представления этого многочлена в конечном виде для частных случаев.
Постановка и решение задачи
Пусть в n+1 различных точках отрезка [x0,xn], удовлетворяющих условию
x0 < x1 < … < xn , заданы значения функции f(x) и ее производных до порядка αi–1 включительно:Вслед за [3, С. 71] будем считать, что производная нулевого порядка есть сама функция, т.е. f(0)(x)= f(x).
Необходимо построить интерполирующую функцию в классе многочленов, которая удовлетворяла бы условиям (1). Для решения задачи введем следующие обозначения.
Поставим в соответствие каждой узловой точке xi функцию ωi(x) определяемую формулой:
![]() (2)
(2)
Функции ωi(x), как это следует из формулы (2), в точках xl ≠xi обращаются в нуль вместе со своими производными до порядка αi–1 включительно и не обращаются в нуль в собственных точках xi, т.е.
![]() (5)
(5)
![]() (6)
(6)
Через ![]() обозначим многочлен Тейлора степени αi –1 для функции f(x), построенный для точки xi, по значениям производных, определенных условием (1):
обозначим многочлен Тейлора степени αi –1 для функции f(x), построенный для точки xi, по значениям производных, определенных условием (1):
![]() (7)
(7)
В некоторых случаях верхний индекс в обозначении ![]() будем опускать.
будем опускать.
Представим H(x) в виде суммы многочленов Hi(x), где Hi(x) строится для каждой узловой точке xi, т.е.
![]() (8)
(8)
Можно записать тождество, верное для всех точек, в которых знаменатель не обращается в нуль:
т.е. выделим из функции f(x) первый сомножитель ωi(x), который в соответствии с (2) обращается в нуль во всех узловых точках, кроме xi, и второй сомножитель f(x)/ωi(x).
Многочлен Hi(x) для каждой узловой точке xi построим в виде произведения двух сомножителей. В качестве первого сомножителя возьмем функцию ωi(x), которая в соответствии с (5) и (6) обладает теми свойствами, что она обращается в нуль сама вместе со своими производными до порядка αi–1 включительно в каждой узловой точке xl, отличной от точки xi. Второй сомножитель f(x)/ωi(x) , так как ωi(xi)≠0, представим в виде многочлена Тейлора для точки xi степени αi–1 включительно с учетом условия (1), что в точке xi заданы производные до порядка αi–1 включительно. В соответствии с рассуждениями, изложенными выше, можно записать, что
![]() (9)
(9)
Подставляя Hi(x) из (9) в (8) получим, что суммарный интерполяционный многочлен H(x) представляется в следующем простом виде:
![]() (11)
(11)
В силу представления H(x) в виде (8) и свойств функции ωi(x), выраженных (5) и (6), следует, что значения H(x) и его производных в точках xi определяются только значениями многочленов Hi(x) и их производных в этих точках, т.е.
Это объясняется тем, что в соответствии с (5) и (6) значения Hi(xj) и их производных в точках xj при j≠i равны нулю.
Многочлен H(x) с учетом представления многочлена Тейлора формулой (7) может быть записан в виде:
![]() (12)
(12)
Степень интерполяционного многочлена
Степень s многочлена H(x) определяется степенями si многочленов Hi(x), которые в свою очередь определяются в соответствии с формулой (9) суммой si степеней сомножителей ωi(x) и ![]() , т.е.
, т.е.
в которой скобками выделены степени сомножителей. Эту формулу для степени si многочлена Hi(x) можно записать в виде:
![]()
из которого видно, что степень si многочлена Hi(x) для всех значений i, определяемых условиями (1), одна и та же.
Из этой формулы и из того, что степень суммы многочленов не превосходит максимума из степеней многочленов суммы, следует, что максимальная степень s многочлена H(x), определяемого (8), выражается формулой:
![]() (13)
(13)
Проверка заданных условий для многочлена
Покажем, что построенный многочлен H(x), представленный формулой (12), удовлетворяет и условиям (1).
Используя формулу для производной j-го порядка произведения двух функций (см. например, [8, С. 149])
![]() (14)
(14)
Далее, вычислим значение этой производной в точке x=xi , заменив обозначение переменной внешнего суммирования i на l:
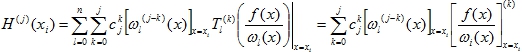 (15)
(15)
Заметим, что при суммировании по переменной l после подстановки x=xi, в силу свойства (5) функции ωi(x) остаются только слагаемые, отвечающие условию l=i, т.е. знак суммирования по l исчезает.
Далее, так как ωi(xi)≠0, то при дифференцировании тождества
![]()
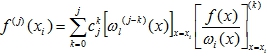 (16)
(16)
Так как правые части формул (15) и (16) равны между собой, то по свойству числовых равенств и левые части равны друг другу, т.е. для всех j = 0,1,…αi–1 и для всех i = 0,1,…n имеет место:
![]()
а это и означает, что построенный многочлен H(x) удовлетворяет условиям (1).
Выделение производных в явном виде
Для того, чтобы выделить значения производных в узловых точках в явном виде, выполним некоторые преобразования. Используя формулу (14) для определения производной j-го порядка от произведения двух функций, формулу (12) для H(x) можно записать в виде:
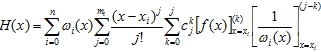
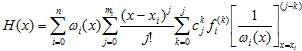 (17)
(17)
Здесь и, далее, буквами mi , i=0,1 обозначены порядки наивысших производных, используемых для построения двухточечного многочлена H(x), т.е.
![]() (18)
(18)
Для того, чтобы вынести обозначения производных из-под знака внутреннего суммирования, в формуле (17) для H(x) поменяем порядок суммирования по переменным j и k и, соответственно, пределы суммирования:
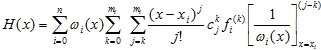
Перейдем к новой переменной суммирования l, определенной формулой l=j–k, из которой следует, что j=l+k. После перехода к переменной l изменятся пределы внутреннего суммирования: при j=k имеет место l=0, при j=mi имеет место l= mi–k. Тогда формула для H(x) примет вид:
![]()
Еще раз поменяем обозначения для внутренних переменных суммирования: k=j и l=k. Тогда H(x) можно записать как
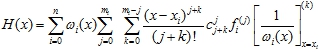
После подстановки в эту формулу выражения для биноминальных коэффициентов (19) и сокращения числителя и знаменателя дроби на (j+k)! получим, что
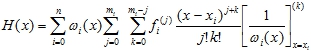 (20)
(20)
Если внести сомножитель ωi(x) под знак суммирования по переменной k, то формулу (20) можно записать как:
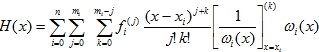
Эта формула для многочлена H(x) с точностью до обозначений (см. формулы (3) и (4)) совпадает с формулой для этого многочлена, приведенной, например в [2, С. 172] и полученной другим путем, что дает дополнительное подтверждение верности представления многочлена в форме (11).
Если в формуле (20) вынести члены, не зависящие от индекса суммирования по k в внешний цикл, то формула для многочлена H(x) примет вид:
![]() (21)
(21)
В соответствии с полученными результатами имеет место следующая теорема.
Теорема
Пусть функция f(x) определена и достаточное число раз дифференцируема на отрезке [x0,xn], а также удовлетворяет условиям (1). Тогда существует многочлен степени не выше s, определенной формулой (13), который представляется в любой из форм (11), (12) или (21).
Интерпретация интерполяционного многочлена
Если в формуле (21) внести сомножитель ωi(x) под знак суммирования по переменной j и сгруппировать сомножители, то формула для H(x) примет следующий вид:
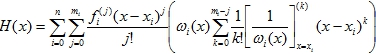 (22)
(22)
и назовем φij(x) поправочной функцией.
С учетом обозначения (23) формулу (22) для H(x) можно записать в виде:
![]() (24)
(24)
Из представления (24) видно, что многочлен, построенный по заданным значениям функции и ее производных в точках отрезка [x0,xn], есть сумма модифицированных многочленов Тейлора, построенных для каждой узловой точки xi этого отрезка. Модификация разложения заключается в том, что каждый член многочлена Тейлора в данной точке xi умножается на поправочную функцию, зависящую как от расстояния до других узловых точек, так и от порядков наивысших известных производных в этих точках.
Практическим следствием указанной интерпретации является то, что для построения интерполяционного многочлена Эрмита, соответствующего заданной функции, можно брать коэффициенты известного представления этой функции в ряд Тейлора в соответствующих узловых точках, не определяя их заново.
Частные случаи многочлена Эрмита. Отметим частные случаи многочлена Эрмита. Предварительно путем последовательного дифференцирования выпишем следующие соотношения для производных функции, выражение для которой является обратным для функции ω(x):
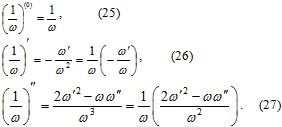
Случай 1
Пусть во всех узловых точках отрезка заданы функции и значения ее первой производной, что соответствует условию:
![]()
С учетом формул для значений производных (25)–(27) формула (22) для многочлена H(x) при обозначении его как H1(x) примет вид:
![]()
С точностью до обозначений эта формула соответствует формуле, приведенной в [3, С. 74] .
Случай 2
Пусть во всех узловых точках отрезка заданы функции и значения ее первой и второй производной, что соответствует условию
![]()
В этом случае формулу (22) для многочлена H(x) при обозначении его как H2(x) с учетом формул для значений производных (25)–(27) можно записать в виде
![]()
Продолжая ряд формул (25)–(27) и используя (22), можно получить аналогичные формулы для многочлена H(x) для последующих значений m=3,4… – максимального порядка заданных в узлах значений производных, не решая частных задач интерполяции для каждого конкретного значения m, как это делается для m=1 в [2, С. 167].
Случай 3
Пусть имеются только две узловые точки, в которых заданы значения функции и ее производных, что соответствует значению n=1. В этом случае общая формула для представления интерполяционного многочлена Эрмита может быть существенно упрощена и доведена до конечного вида.
Формула (3) для ωi(x) с учетом (4) записывается в виде
![]() (28)
(28)
С использованием (28) легко устанавливается, что производная k-го порядка от обратной величины ωi(x) представляется как
![]()
и используя выражение для биномиального коэффициента ![]() , определенного (19), получим конечную формулу для двухточечного интерполяционного многочлена Эрмита
, определенного (19), получим конечную формулу для двухточечного интерполяционного многочлена Эрмита
![]() (30)
(30)
которая соответствует представлению этого многочлена, полученному в [9, С. 1080].
Подробное исследование этого случая и применение двухточечных интерполяционных многочленов Эрмита для аппроксимации функций при симметричном и несимметричном распределении производных на концах отрезка и его оптимизация проведено в [9] и [10], соответственно.
Заключение
В работе осуществлен простой вывод формулы интерполяционного многочлена Эрмита на основе использования многочлена Тейлора. Предложена интерпретация многочлена Эрмита как сумма модифицированных многочленов Тейлора, построенных для каждой из узловых точек. Указан алгоритм получения конечных формул для этих многочленов в случае, когда максимальные порядки производных, заданных в узловых точках, одинаковы.
Список литературы / References
- Hermite Sh. Sur la formule d'interpolation de Lagrange / Sh. Hermite // Journal fur die reine und angewandte Mathematik. – 1878. – Vol. 84. – P. 70–79.
- Березин И. С. Методы вычислений. Т. 1 / И. С. Березин, Н. П. Жидков – М.: Физматлит, 1962. – 464 с.
- Гончаров В.И. Теория интерполирования и приближения функций. / В. И. Гончаров. – М.: Гостехтеориздат, 1934. – 316 с.
- Прасолов В. В. Многочлены. / В. В. Прасолов – М.: МЦНМО. – 1999. – 336с.
- Микеладзе Ш. Е. Численные методы математического анализа. / Ш. Е. Микеладзе – М.: Гостехтеориздат, 1953. – 528 с.
- Spitzbart A. A generalization of Hermite's interpolation formula / A. Spitzbart // Amer. Math. Monthly, 1960. – 67. – P. 42–46.
- Stanica D. A short proof of the Hermite’s formula for polynomial interpolation using operator methods / D. Stanica // Annals of the Alexandru Ioan Cuza University – Mathematics. – 2015. – Vol 61. – P. 209–215. doi: 10.2478/aicu-2013-0040
- Кудрявцев Л. Д. Математический анализ. Т. 1. / Л. Д. Кудрявцев – М.: Высшая школа, 1970. – 590 с.
- Шустов В. В. О приближении функций двухточечными интерполяционными многочленами Эрмита / В. В. Шустов // Журнал вычислительной математики и математической физики. – 2015. – Т. 55. – № 7. – С. 1091–1108.
- Шустов В. В. Аппроксимация функций несимметричными двухточечными многочленами Эрмита и ее оптимизация / В. В. Шустов // Журнал вычислительной математики и математической физики. – 2015. – Т. 55. – № 12. – С. 1999–2014.
Список литературы на английском языке / References in English
- Hermite Sh. Sur la formule d'interpolation de Lagrange / Sh. Hermite // Journal fur die reine und angewandte Mathematik. – 1878. – Vol. 84. – P. 70–79.
- Berezin I. S. Computing Methods. / I. S. Berezin, N. P. Zhidkov. Vol. 1 – Pergamon: Oxford, 1965. – 464 P.
- Goncharov V. I. Teoriya interpolirovaniya i priblizheniya funktsij [The theory of interpolation and approximation of functions] / V. I. Goncharov. – M.: Gostekhteorizdat, 1934. – 316 P. [in Russian]
- Prasolov V. V. Mnogochleny [Polynomials] / V. V. Prasolov. – М.: МTSNMO, 1999. – 336 P. [in Russian]
- Mikeladze Sh. E. Chislennye metody matematicheskogo analiza [Numerical methods of mathematical analysis] / Sh. E. Mikeladze. – M.: Gostekhteorizdat, 1953. – 528 P. [in Russian]
- Spitzbart A. A generalization of Hermite's interpolation formula / A. Spitzbart // Amer. Math. Monthly, 1960. – Vol. 67. – P. 42–46.
- Stanica D. A short proof of the Hermite’s formula for polynomial interpolation using operator methods / D. Stanica // Annals of the Alexandru Ioan Cuza University – Mathematics. – 2015. – Vol 61. – P. 209–215. doi: 10.2478/aicu-2013-0040
- Kudryavtsev L. D. Matematicheskij analiz [Mathematical analysis] T. 1 / L. D. Kudryavtsev – M: Vysshaya Shkola, 1970. – 590 P. [in Russian]
- Shustov V. V. Approximation of functions by two-point Hermite interpolating polynomials / V. V. Shustov // Computational Mathematics and Mathematical Physics. – 2015. – Vol. 55. – No 7. – P. 1077–1093. doi: 10/1134/S0965542515040156
- Shustov V. V. Approximation of functions by asymmetric two-point Hermite polynomials and its optimization / V. V. Shustov // Computational Mathematics and Mathematical Physics. – 2015. – Vol. 55. – No 12. – P. 1960–1974. doi: 10/1134/S0965542515120155
