МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДИНАМИКИ МАССО- И ТЕПЛОПЕРЕНОСА В ПРОЦЕССАХ ЭЖЕКЦИИ И ИНЖЕКЦИИ
Петросян О.П.1, Кожевников А.Б.2, Горбунов А.К.3, Рябченков Д.В.4, Кулюкина А.О.5
1Кандидат физико-математических наук, доцент, 2Кандидат технических наук, 3Доктор физико-математических наук, профессор, 4Аспирант, 5Аспирант, Калужский филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Московский государственный технический университет имени Н.Э. Баумана (национальный исследовательский университет)» (КФ МГТУ им. Н.Э. Баумана)
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДИНАМИКИ МАССО- И ТЕПЛОПЕРЕНОСА В ПРОЦЕССАХ ЭЖЕКЦИИ И ИНЖЕКЦИИ
Аннотация
Динамика рассматриваемого класса объектов и систем водоподготовки в общем случае описывается линейными или линеаризованными дифференциальными уравнениями с частными производными и постоянными или переменными коэффициентами, существование и единственность решения которых обеспечены необходимыми и достаточными линейными краевыми условиями.
Такое же математическое описание имеют, в частности, процессы тепло- и массопереноса используемые технологических процессах на объектах водоподготовки. Определение обобщенных динамических характеристик этих процессов с учетом взаимосвязи тепло- и массообмена позволит решить задачи анализа, синтеза автоматизированной или автоматической системы управления такими агрегатами, а также задачи совершенствования технологии и модернизации оборудования с целью улучшения качественных характеристик продукции, снижения энергетических затрат на ее производство и повышения производительности технологических агрегатов.
Ключевые слова: математическое моделирование, массо- или теплоперенос, краевые задачи, распределенные звенья, преобразования Лапласа.
Petrosyan O.P.1, Kozhevnikov A.B.2, Gorbunov A.K.3, Ryabchenkov D.V.4, Kuluikina A.O. 5
1PhD in Physics and Mathematics, Associate Professor, Kaluga Branch of the Federal State Budget Educational Institution of Higher Professional Education “Bauman Moscow State Technical University (National Research University)”, 2PhD in Engineering, Kaluga Branch of the Federal State Budget Educational Institution of Higher Professional Education “Bauman Moscow State Technical University (National Research University)”, 3PhD in Physics and Mathematics, Professor, Kaluga Branch of the Federal State Budget Educational Institution of Higher Professional Education “Bauman Moscow State Technical University (National Research University)”, 4Postgraduate Student, Kaluga Branch of the Federal State Budget Educational Institution of Higher Professional Education “Bauman Moscow State Technical University (National Research University)”, 5Postgraduate Student, Kaluga Branch of the Federal State Budget Educational Institution of Higher Professional Education “Bauman Moscow State Technical University (National Research University)”
MATHEMATICAL MODELING OF THE DYNAMICS OF MASS- AND HEAT TRANSFER IN EJECTION AND INJECTION PROCESSES
Abstract
The dynamics of the considered class of objects and water treatment systems in the general case is described by linear or linearized differential equations with partial derivatives and constant or variable coefficients, the existence and uniqueness of the solution of which are provided by necessary and sufficient linear boundary conditions.
The same mathematical description has, in particular, the processes of heat and mass transfer used by technological processes at water treatment facilities. Taking into account the interrelation of heat and mass transfer, determination of the generalized dynamic characteristics of these processes will allow solving the problems of analysis and synthesis of an automated or automatic control system for such units, as well as the tasks of improving technology and upgrading equipment in order to improve quality characteristics of products, reduce energy costs for its production and enhance the productivity of technological units.
Keywords: mathematical modeling, mass or heat transfer, boundary value problems, distributed components, Laplace transformation.
Дадим математическое описание широкого класса технологических объектов и систем в технологиях водоподготовки, на исследовании которых можно достаточно полно охарактеризовать особенности детерминированного анализа таких систем и использовать результаты при исследовании конкретных технологических объектов. К ним следует отнести различные по назначению аппараты, в которых происходят физические процессы массообмена и теплообмена, как правило, взаимосвязанные между собой. Это аппараты, принцип действия которых основан на таких явлениях как эжекция, инжекция, сорбция, десорбция, растворение и т.п., которых весьма достаточно в технологиях водоподготовки и сопутствующих технологиях, например, подготовка растворов, нейтрализация активных отходов, нейтрализация аварийных ситуаций и другие. Дадим математическое описание таких объектов и систем.
Динамика изменения массосодержания ![]() и температуры
и температуры ![]() среды или материала при отсутствии градиента общего давления описывается следующей системой дифференциальных уравнений [1, C. 560]:
среды или материала при отсутствии градиента общего давления описывается следующей системой дифференциальных уравнений [1, C. 560]:
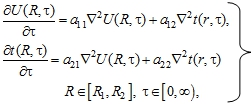 (1)
(1)
где ![]() - нормированная координата; R0 - основной геометрический параметр среды или материала;
- нормированная координата; R0 - основной геометрический параметр среды или материала; ![]() - оператор Лапласа по R [1, C. 560]; коэффициенты
- оператор Лапласа по R [1, C. 560]; коэффициенты ![]() постоянны.
постоянны.
Единственность решения этой системы дифференциальных уравнений обеспечивается начальными и граничными условиями, которые в общем случае можно записать следующим образом:
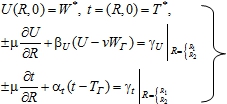 (2)
(2)
Начальные значения ![]() постоянны, а значение коэффициента v - рассчитываемая величина. Остальные коэффициенты, входящие в граничные условия, равны: при граничных условиях первого рода
постоянны, а значение коэффициента v - рассчитываемая величина. Остальные коэффициенты, входящие в граничные условия, равны: при граничных условиях первого рода ![]() , второго рода -
, второго рода - ![]() постоянны; третьего рода -
постоянны; третьего рода - ![]() , а для коэффициентов
, а для коэффициентов ![]() допустимо изменение во времени.
допустимо изменение во времени.
Массосодержание WГ и температура TГ пограничной среды либо заданы и постоянны, либо являются решением определенных уравнений, о чем будет сказано позднее.
Осреднение внутреннего поля массосодержания U и температуры t по объему среды или материала V позволяет определить изменение во времени среднеобъемного массосодержания среды или материала ![]() и среднеобъемной температуры
и среднеобъемной температуры ![]() :
:
При ![]() или малом взаимном влиянии друг на друга процессов переноса каждой из субстанций (массы и тепла) система уравнений (1) распадается на два самостоятельных дифференциальных уравнения, описывающих массо- или теплоперенос [2, C. 432], каждое из которых можно записать в следующем виде (уравнение Фурье):
или малом взаимном влиянии друг на друга процессов переноса каждой из субстанций (массы и тепла) система уравнений (1) распадается на два самостоятельных дифференциальных уравнения, описывающих массо- или теплоперенос [2, C. 432], каждое из которых можно записать в следующем виде (уравнение Фурье):
![]() (5)
(5)
Как правило, рассматриваемые процессы протекают в закрытых системах (трубопроводы, каналы, камеры и т.п.), т.е. таких, для которых справедливы уравнения материального и теплового баланса, в которые входят ![]() и
и ![]() . Причем, для учета теплопотерь в окружающую среду необходимо рассмотреть динамику теплообмена между движущейся по трубопроводу или иному каналу средой (жидкостью, газом) и окружающей эту трубу внешней средой через ее стенку, имеющую температуру
. Причем, для учета теплопотерь в окружающую среду необходимо рассмотреть динамику теплообмена между движущейся по трубопроводу или иному каналу средой (жидкостью, газом) и окружающей эту трубу внешней средой через ее стенку, имеющую температуру ![]() . Этот процесс описывается следующей системой дифференциальных уравнений
. Этот процесс описывается следующей системой дифференциальных уравнений
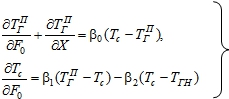 (6)
(6)
В системе (7.6) независимыми переменными являются безразмерные ![]() , которые связаны со временем τ и продольной координатой трубы x соотношениями
, которые связаны со временем τ и продольной координатой трубы x соотношениями
![]() (7)
(7)
Решение системы уравнений (6) позволит определить изменение температуры пограничного потока в трубе ![]() с учетом теплообмена с окружающей средой
с учетом теплообмена с окружающей средой
![]() (8)
(8)
![]() (9)
(9)
Часто применяемые режимы работы таковы, что можно считать, что взаимное влияние процессов массообмена и теплообмена друг на друга не существенно, т.е. массообмен не осложнен теплообменом, так как температура среды или материала T в процессе изменяется незначительно. Такой массообмен описывается дифференциальным уравнением
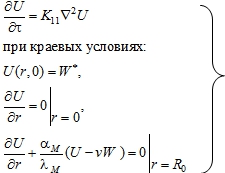 (10)
(10)
Если ограничиться лишь применяемыми режимами работы установки, то для расчета изменения массосодержания материала достаточно решения краевой задачи (10). Решение же системы уравнений (6) позволит исследовать и оценить возможности перехода на иные режимы работы установки, способствующие повышению ее производительности и улучшению качества продукции.
Уточним некоторые параметры системы (10). Коэффициент массоотдачи ![]() , входящий в граничные условия, по мере увеличения скорости материала убывает и его изменение во времени можно описать следующей зависимостью
, входящий в граничные условия, по мере увеличения скорости материала убывает и его изменение во времени можно описать следующей зависимостью
![]() (11)
(11)
Массообменные характеристики процесса зависят от значения коэффициента массопоглощения v, который также входит в граничные условия и рассчитывается с учетом специфики рассматриваемого процесса. Физический смысл и формулы вычисления остальных параметров, входящих в вышеприведенные уравнения математической модели исследуемых объектов и систем, уточняются в конкретных задачах.
К искомым динамическим характеристикам относятся пространственно-временные характеристики ![]() , их осреднения по объему
, их осреднения по объему ![]() и
и ![]() , а также
, а также ![]() , являющиеся решениями соответствующих уравнений математической модели. Как показано в последующих главах, соответствующей заменой искомых функций в этих дифференциальных уравнениях можно получить их более обобщенные решения, позволяющие судить о поведении системы при изменении начальных условий, граничных условий, параметров среды и некоторых параметров процесса, т.е. получить обобщенные динамические характеристики системы. Кроме того, в ходе решения дифференциальных уравнений математической модели можно выявить так называемые элементарные распределенные звенья [3, C. 304], [9, С. 46 – 53], динамические характеристики которых также следует отнести к искомым, так как при их наличии определение динамических характеристик всей системы или составляющих ее частей не вызывает затруднений.
, являющиеся решениями соответствующих уравнений математической модели. Как показано в последующих главах, соответствующей заменой искомых функций в этих дифференциальных уравнениях можно получить их более обобщенные решения, позволяющие судить о поведении системы при изменении начальных условий, граничных условий, параметров среды и некоторых параметров процесса, т.е. получить обобщенные динамические характеристики системы. Кроме того, в ходе решения дифференциальных уравнений математической модели можно выявить так называемые элементарные распределенные звенья [3, C. 304], [9, С. 46 – 53], динамические характеристики которых также следует отнести к искомым, так как при их наличии определение динамических характеристик всей системы или составляющих ее частей не вызывает затруднений.
Частные случаи сформулированной выше математической модели нашли применение не только в теории тепло- и (или) массообмена [4, C. 132], [1, C. 560], но и в задачах математической физики [5, С. 33 – 40], [6, C. 712], [11, C. 352], в радиотехнике, при описании процессов в аппаратах химической технологии [7, C. 168] и других.
Дифференциальные уравнения этой математической модели не имеют точного решения, а их приближения, которые могут быть получены различными методами, не гарантируют, прежде всего, достаточной скорости сходимости аппроксимирующих выражений, за исключением ряда упрощенных описаний таких процессов [5, С. 33 – 40], [8, C. 720].
В процессе решения вышеприведенных краевых задач будем применять математический аппарат одномерного и двумерного преобразования Лапласа.
При постоянных коэффициентах ![]() и в граничных условиях (2) можно получить решения дифференциальных уравнений описанной выше математической модели в изображениях по Лапласу, т.е. как функции параметра интегрального преобразования s и координаты R или X, если воспользоваться преобразованием Лапласа по
и в граничных условиях (2) можно получить решения дифференциальных уравнений описанной выше математической модели в изображениях по Лапласу, т.е. как функции параметра интегрального преобразования s и координаты R или X, если воспользоваться преобразованием Лапласа по ![]() или [4, C. 132]. Так, при граничных условиях первого, второго или третьего рода в этом случае по дифференциальному уравнению Фурье можно получить [4, C. 132]
или [4, C. 132]. Так, при граничных условиях первого, второго или третьего рода в этом случае по дифференциальному уравнению Фурье можно получить [4, C. 132]
![]() (12)
(12)
где ![]() – коэффициенты, определяемые граничными условиями, а
– коэффициенты, определяемые граничными условиями, а ![]() – передаточные функции по соответствующим каналам воздействия. Как
– передаточные функции по соответствующим каналам воздействия. Как ![]() содержат в своей структуре гиперболические функции, если объект имеет форму пластины или шара, а при объекте цилиндрической формы – функции Бесселя. Их конкретные выражения для этих трех основных форм тела даны в работах [4, C. 132].
содержат в своей структуре гиперболические функции, если объект имеет форму пластины или шара, а при объекте цилиндрической формы – функции Бесселя. Их конкретные выражения для этих трех основных форм тела даны в работах [4, C. 132].
В ряде случаев передаточные функции распределенных объектов содержат трансцендентные составляющие вида
![]() (13)
(13)
Такие сомножители с дробно-рациональной функцией ![]() определяют передаточные функции теплообменных аппаратов [7, C. 168], а с дробно-иррациональной функцией
определяют передаточные функции теплообменных аппаратов [7, C. 168], а с дробно-иррациональной функцией ![]() – изображения по Лапласу динамических характеристик связанного тепломассопереноса, являющихся решением системы дифференциальных уравнений (1) [3, C. 304], [10, С. 17 – 28].
– изображения по Лапласу динамических характеристик связанного тепломассопереноса, являющихся решением системы дифференциальных уравнений (1) [3, C. 304], [10, С. 17 – 28].
Список литературы / References
- Лыков А.В. Тепломассообмен / Лыков А.В. // Справочник – М: Энергия, 1972. – С. 560.
- Лыков М.В. Сушка в химической промышленности / Лыков М.В. // Сушка в химической промышленности – М: Химия, 1970. – С. 432.
- Кожевников А.Б., Петросян О.П. Спектральная оптимизация в задачах анализа и синтеза систем / Кожевников А.Б., Петросян О.П. // Спектральная оптимизация в задачах анализа и синтеза систем – Калуга: Монускрипт, 2016. – С. 304.
- Кожевников А. Б., Петросян О. П. Эжекция и сушка материалов в режиме пневмотранспорта / Кожевников А. Б., Петросян О. П. // Эжекция и сушка материалов в режиме пневмотранспорта – М: Изд-во МГТУ им. Н. Э. Баумана. – 2010. – C. 142.
- Дмитриев А.Н., Кожевников А.Б. Применение математического программирования в спектральных методах детерминированного и статистического анализа систем с переменными параметрами. / Дмитриев А.Н., Кожевников А.Б. // – В кн.: Автоматическое управление объектами с переменными характеристиками. Межвузовский сборник научных трудов, Новосибирск. – 1989. – С. 33 – 40.
- Кошляков Н.С., Глинер Э.Б., Смирнов М.М. Уравнения в частных производных математической физики / Кошляков Н.С., Глинер Э.Б., Смирнов М.М. // Уравнения в частных производных математической физики – М: Высшая школа. – 1970. – С. 712.
- Серов Е.П., Корольков Б.П. Динамика процессов в тепло- и массообменных аппаратах / Серов Е.П., Корольков Б.П. // Динамика процессов в тепло- и массообменных аппаратах – М: Энергия. – 1967. – С. 168.
- Корн Г. и Корн Т. Справочник по математике для научных работников и инженеров / Корн Г. и Корн Т. // – Справочник по математике для научных работников и инженеров – М: Наука. – С. 720.
- Кожевников А.Б., Петросян О.П. Спектральная адаптация метода наименьших квадратов к динамике объектов водоподготовки с распределенными параметрами. / Кожевников А.Б., Петросян О.П. // Водоочистка, Водоподготовка, Водоснабжение. – 2010. – № 10. – С. 46-53.
- Кожевников А.Б., Петросян О.П. Расчет динамики распространения по водной сети зон загрязнения в нестационарных условиях / Кожевников А.Б., Петросян О.П. // Водоснабжение и канализация. – 2010. – № 9. – С. 17-28.
- Алексидзе М.А. Решение граничных задач методом разложения по неортогональным функциям / Алексидзе М.А. // Решение граничных задач методом разложения по неортогональным функциям – М: Наука. – 1978. – C. 352.
Список литературы на английском языке / References in English
- Lykov A.V. Teplomassoobmen [Heat and mass transfer] / Lykov A.V. // Spravochnik [handbook] – M: Jenergija, 1972. – P. 560. [in Russian]
- Lykov M.V. Sushka v himicheskoj promyshlennosti [Drying in the chemical industry] / Lykov M.V. // Sushka v himicheskoj promyshlennosti [Drying in the chemical industry] – M: Himija, 1970. – P. 432. [in Russian]
- Kozhevnikov A.B., Petrosjan O.P. Spektral'naja optimizacija v zadachah analiza i sinteza system [Spectral optimization in problems of analysis and synthesis of systems] / Kozhevnikov A.B., Petrosjan O.P. // Spektral'naja optimizacija v zadachah analiza i sinteza sistem [Spectral optimization in problems of analysis and synthesis of systems] – Kaluga: Monuskript, 2016. – P. 304. [in Russian]
- Kozhevnikov A. B., Petrosjan O. P. Jezhekcija i sushka materialov v rezhime pnevmotransporta [Ejection and drying of materials in pneumatic transport mode] / Kozhevnikov A. B., Petrosjan O. P. // Jezhekcija i sushka materialov v rezhime pnevmotransporta [Ejection and drying of materials in pneumatic transport mode] – M: Izd-vo MGTU im. N. Je. – 2010. – P. 142. [in Russian]
- Dmitriev A.N., Kozhevnikov A.B. Primenenie matematicheskogo programmirovanija v spektral'nyh metodah determinirovannogo i statisticheskogo analiza sistem s peremennymi parametrami [Application of mathematical programming in the spectral methods of deterministic and statistical analysis of systems with variable parameters] / Dmitriev A.N., Kozhevnikov A.B. // – V kn.: Avtomaticheskoe upravlenie obektami s peremennymi harakteristikami. Mezhvuzovskij sbornik nauchnyh trudov, Novosibirsk [Automatic control of objects with variable characteristics. Interuniversity collection of scientific papers, Novosibirsk] – 1989. – P. 33 – 40. [in Russian]
- Koshljakov N.S., Gliner Je.B., Smirnov M.M. Uravnenija v chastnyh proizvodnyh matematicheskoj fiziki [Equations in partial derivatives of mathematical physics] / Koshljakov N.S., Gliner Je.B., Smirnov M.M. // Uravnenija v chastnyh proizvodnyh matematicheskoj fiziki [Equations in partial derivatives of mathematical physics] – M: Vysshaja shkola. – 1970. – P. 712. [in Russian]
- Serov E.P., Korol'kov B.P. Dinamika processov v teplo- i massoobmennyh apparatah [Dynamics of processes in heat and mass transfer apparatus] / Serov E.P., Korol'kov B.P. // Dinamika processov v teplo- i massoobmennyh apparatah [Dynamics of processes in heat and mass transfer devices] – M: Jenergija. – 1967. – P. 168. [in Russian]
- Korn G. i Korn T. Spravochnik po matematike dlja nauchnyh rabotnikov i inzhenerov [A handbook on mathematics for scientists and engineers] / Korn G. i Korn T. // – Spravochnik po matematike dlja nauchnyh rabotnikov i inzhenerov [A handbook on mathematics for scientists and engineers] – M: Nauka. 1968. – P. 720. [in Russian]
- Kozhevnikov A.B., Petrosjan O.P. Spektral'naja adaptacija metoda naimen'shih kvadratov k dinamike obektov vodopodgotovki s raspredelennymi parametrami [Spectral adaptation of the method of least squares to the dynamics of water treatment objects with distributed parameters] / Kozhevnikov A.B., Petrosjan O.P. // Vodoochistka, Vodopodgotovka, Vodosnabzhenie [Water treatment, Water treatment, Water supply] – 2010. – № 10. – P. 46-53. [in Russian]
- Kozhevnikov A.B., Petrosjan O.P. Raschet dinamiki rasprostranenija po vodnoj seti zon zagrjaznenija v nestacionarnyh uslovijah [Calculation of the dynamics of propagation of contaminated zones over the water network in non-stationary conditions] / Kozhevnikov A.B., Petrosjan O.P. // Vodosnabzhenie i kanalizacija [Water supply and sewerage] – 2010. – № 9. – P. 17-28. [in Russian]
- Aleksidze M.A. Reshenie granichnyh zadach metodom razlozhenija po neortogonal'nym funkcijam [Solution of boundary value problems by the method of expansion in non-orthogonal functions] / Aleksidze M.A. // Reshenie granichnyh zadach metodom razlozhenija po neortogonal'nym funkcijam [Solution of Boundary Problems by the Method of Expansion in Nonorthogonal Functions] – M: Nauka. – 1978. – P. 352. [in Russian]
