МАТЕМАТИЧЕСКИЕ МОДЕЛИ КОНКУРЕНЦИИ НА ТРОФИЧЕСКОМ РЕСУРСЕ
МАТЕМАТИЧЕСКИЕ МОДЕЛИ КОНКУРЕНЦИИ НА ТРОФИЧЕСКОМ РЕСУРСЕ
Научная статья
Горыня Е.В.1, Колпак Е.П.2, *
1 ORCID: 0000-0001-5578-1359;
2 ORCID: 0000-0001-6956-4814;
1, 2 Санкт-Петербургский государственный университет, Санкт-Петербург, Россия
* Корреспондирующий автор (maltceva_pmpu[at]mail.ru)
АннотацияРазработаны математические модели эксплуатационной и интерференционной конкуренций на линейном ареале на основе систем уравнений с распределенными параметрами. Сделан анализ стационарных состояний на устойчивость. Показано, что эксплуатационная конкуренция на восстанавливаемом трофическом ресурсе не приводит к исчезновению одной из популяций, обусловленной конкуренцией. Модель интерференционной конкуренции содержит различные варианты последствий конкуренции двух популяций. В обоих моделях для популяций с малым числом особей влияние конкуренции не существенно. Дана оценка скоростей распространения малочисленных популяций на ареале. Получены условия существования автоволнового решения на неограниченной прямой. Для построения численного решения краевой задачи для системы нелинейных дифференциальных уравнений используется метод сеток с программной реализацией в среде программирования математического пакета Matlab. Численные результаты согласуются с аналитическими результатами на мелких сетках.
Ключевые слова: популяция, конкуренция, трофический ресурс, устойчивость, дифференциальные уравнения.
MATHEMATICAL COMPETITIVE MODELS ON THE TROPHIC RESOURCE
Research article
Gorynya E.V.1, Kolpak E.P.2, *
1 ORCID: 0000-0001-5578-1359;
2 ORCID: 0000-0001-6956-4814;
1, 2 St. Petersburg State University, St. Petersburg
* Corresponding author (maltceva_pmpu[at]mail.ru)
AbstractThe authors have developed mathematical models of operational and interference competition on a linear range based on the systems of equations with distributed parameters. They also have conducted an analysis of stationary states stability. It is shown that the operational competition on the restored trophic resource does not lead to the disappearance of one of the populations due to competition. The model of interference competition contains various options for the effects of competition between the two populations. In both models, for populations with a small number of individuals, the influence of competition is not significant. The assessment of the distribution rates of small populations on the range is given, and the conditions for the existence of an autowave solution on an unbounded straight line are obtained. In order to construct a numerical solution of a boundary value problem for a system of nonlinear differential equations, they have used the grid method with software implementation in the programming environment of the Matlab environment. Numerical results are consistent with analytical results on fine grids.
Keywords: population, competition, trophic resource, stability, differential equations.
ВведениеОдна из первых моделей конкуренции была предложена Вольтерра [1] как модель видов, оспаривающих одну и ту же пищу. Для случая n популяций, численность которых ![]() живущих на одной территории, питающихся одним и тем же пищевым ресурсом модель динамика популяций записывается в форме
живущих на одной территории, питающихся одним и тем же пищевым ресурсом модель динамика популяций записывается в форме
![]() (1)
(1)
где ![]() - постоянные величины,
- постоянные величины, ![]() ‑ положительно определенная функция, характеризующая уровень конкурентного взаимодействия популяций.
‑ положительно определенная функция, характеризующая уровень конкурентного взаимодействия популяций.
Из анализа уравнений (1) следует, что выживает только та популяция, у которой наибольшее значение ![]() а остальные погибают [1], [2]. В результате был сформулирован принцип конкурентного исключения, в соответствии с которым должно уменьшаться число видов, энергетические потребности на воспроизводство потомства которых больше, чем у конкурирующих с ними видов [3], [4].
а остальные погибают [1], [2]. В результате был сформулирован принцип конкурентного исключения, в соответствии с которым должно уменьшаться число видов, энергетические потребности на воспроизводство потомства которых больше, чем у конкурирующих с ними видов [3], [4].
В модели (1) в случае одиночной популяции ее численность со временем неограниченно увеличивается. Но за миллионы лет существования всего живого на Земле такой прогноз не подтверждаются. Нет и примеров постоянного увеличения численности какой-либо популяции на историческом временном интервале. Есть и многочисленные примеры «мирного» существования на общем трофическом ресурсе различных популяций [3], [4]. Наблюдается конкуренция и между отдельными группами особей внутри самой популяции [3], [5], обусловленная внешними и внутренними причинами. Учет внутривидовой и межвидовой конкуренций осуществлен в модели [3], [5].
![]() (2)
(2)
где ![]() – положительные постоянные.
– положительные постоянные.
Модель (2) при ![]() описывает n логистических популяций с ограниченными емкостями сред
описывает n логистических популяций с ограниченными емкостями сред ![]() , устойчивым решением
, устойчивым решением ![]() . При малых значениях
. При малых значениях ![]() по сравнению с
по сравнению с ![]() нетривиальная стационарная точка, имеющая физический смысл, в силу непрерывности решения от параметров может быть устойчивой [2]. Таким образом, в модели (2) численность одиночной популяции ограничивается емкостью среды и допускается возможность устойчивого существования конкурирующих популяций. Но отсутствуют ресурсы, на которых происходит конкурентное взаимодействие популяций. То есть функция
нетривиальная стационарная точка, имеющая физический смысл, в силу непрерывности решения от параметров может быть устойчивой [2]. Таким образом, в модели (2) численность одиночной популяции ограничивается емкостью среды и допускается возможность устойчивого существования конкурирующих популяций. Но отсутствуют ресурсы, на которых происходит конкурентное взаимодействие популяций. То есть функция ![]() в (1) и в (2) отражает непосредственный контакт между особями, приводящий к уменьшению скорости их роста. Но это может рассматриваться как простое взаимное уничтожение. Если считать, что эта функция отражает конкуренцию на неограниченном ресурсе, то в этом случае не просто объяснить, в чем ее суть, поскольку ресурса достаточно для всех популяций.
в (1) и в (2) отражает непосредственный контакт между особями, приводящий к уменьшению скорости их роста. Но это может рассматриваться как простое взаимное уничтожение. Если считать, что эта функция отражает конкуренцию на неограниченном ресурсе, то в этом случае не просто объяснить, в чем ее суть, поскольку ресурса достаточно для всех популяций.
Введение трофического ресурса S в модель (2) можно осуществить следующим образом
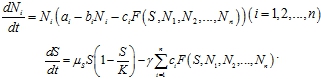
Здесь предполагается, что изменение количества ресурса, если он не потребляется, описывается логистическим уравнением. Параметр ![]() ‑ удельная скорость роста ресурса,
‑ удельная скорость роста ресурса, ![]() ‑ положительный параметр.
‑ положительный параметр.
Модели (1) и (2) описывают интерференционную конкуренцию [3]. Эксплуатационную конкуренцию, которая свойственна видам, потребляющим одну и ту же пищу без непосредственного взаимодействия особей друг с другом, эти модели не содержат. Для описания такой конкуренции необходимо считать, что собственная скорость роста численности популяции зависит от количества потребляемого ресурса, а ресурс рассматривается как «жертва» по отношению к популяции его потребляющей. Модель, в отличие от (2) может быть записана в форме
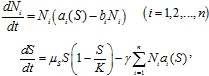
где ![]() ‑ функции, задающие скорость размножения популяции.
‑ функции, задающие скорость размножения популяции.
Эксплуатационная конкуренция
Для учета влияния на линейном ареале пищевого ресурса S на численность двух популяций, линейная плотность которых ![]() , предполагается, что скорость размножения особей популяций зависит от количества потребляемой пищи. При изобилии ресурса он не должен влиять на скорость роста численности популяции, а в его отсутствие скорость роста численности равна нулю. Этим условиям удовлетворяет гиперболическая зависимость:
, предполагается, что скорость размножения особей популяций зависит от количества потребляемой пищи. При изобилии ресурса он не должен влиять на скорость роста численности популяции, а в его отсутствие скорость роста численности равна нулю. Этим условиям удовлетворяет гиперболическая зависимость: ![]() , где b ‑ положительная константа.
, где b ‑ положительная константа.
С учетом этих предположений модель конкуренции двух логистических популяций на неподвижном трофическом записывается в форме системы уравнений с распределенными параметрами
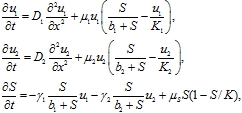 (3)
(3)
где ![]() ‑ скорости роста численности популяций на неограниченном ресурсе и трофического ресурса в отсутствие популяций,
‑ скорости роста численности популяций на неограниченном ресурсе и трофического ресурса в отсутствие популяций, ![]() ‑ емкости сред популяций и трофического ресурса, параметры
‑ емкости сред популяций и трофического ресурса, параметры ![]() характеризуют подвижность особей,
характеризуют подвижность особей, ![]() ‑ положительные постоянные.
‑ положительные постоянные.
На границах отрезка длиной l ставятся условия наполнения среды [6]:
![]()
![]()
где ![]() – дельта функция Дирака.
– дельта функция Дирака. ![]()
Локальная модель следует из (3) в предположении, что ![]() . Тривиальная стационарная точка в этой модели будет неустойчивой, поскольку одно из собственных значений матрицы Якоби будет положительным:
. Тривиальная стационарная точка в этой модели будет неустойчивой, поскольку одно из собственных значений матрицы Якоби будет положительным: ![]() . В нетривиальной неподвижной точке
. В нетривиальной неподвижной точке
![]()
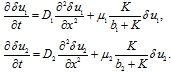 (7)
(7)
Решения этих уравнений как функции времени будут расти по экспоненциальной зависимости с показателем ![]() и показателем
и показателем ![]() . Физическая интерпретация этого: при малом числе особей двух конкурирующие популяции они не оказывают влияния друг на друга, а численность обеих популяций будет увеличиваться.
. Физическая интерпретация этого: при малом числе особей двух конкурирующие популяции они не оказывают влияния друг на друга, а численность обеих популяций будет увеличиваться.
Для неограниченной прямой и условий (5) из (7) следуют выражения для ![]() [6]
[6]

Из выражений для ![]() следует, что распространение популяций из точки
следует, что распространение популяций из точки ![]() на отрезок в первом приближении будет происходить со скоростями
на отрезок в первом приближении будет происходить со скоростями
![]()
Решения, на которых одновременно ![]() , находятся как корни системы уравнений
, находятся как корни системы уравнений
На промежутке ![]() функция
функция ![]() меняет знак. Поэтому эта система уравнений будет иметь хотя бы один положительный корень.
меняет знак. Поэтому эта система уравнений будет иметь хотя бы один положительный корень.
Автоволновое решение
Нелинейные уравнения, имеющие несколько стационарных решений, могут иметь автоволновые решения [6], [7], [8]. Скорости распространения двух популяций на неограниченном ареале, как это следует из (8), должны быть разными. Тогда автоволновое решение представляется в виде функций одного аргумента ![]() , и, соответственно, должно удовлетворять уравнениям
, и, соответственно, должно удовлетворять уравнениям
 (9)
(9)
где ![]() .
.
Решение уравнений (9) ищется с условиями:
- При
![]()
а S является корнем уравнения
![]()
- При
![]()
Возмущения ![]() уравнений (9) в силу их малости около первой стационарной точки удовлетворяют линейным уравнениям
уравнений (9) в силу их малости около первой стационарной точки удовлетворяют линейным уравнениям
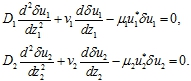 (10)
(10)
Характеристические числа этих уравнений имеют корни противоположных знаков, поэтому в окрестности этой стационарной точки можно построить такое решение, на котором функции ![]() и будут убывать с ростом
и будут убывать с ростом ![]() .
.
Пусть скорость второй автоволны меньше, чем скорость первой. Тогда, поскольку первая автоволна опережает вторую, возмущение ![]() в окрестности точки
в окрестности точки ![]() , удовлетворяет уравнению
, удовлетворяет уравнению
![]()
которое и будет условием существования убывающего решения в окрестности точки ![]() для первого уравнения в (10), и, одновременно условием возможного существования автоволнового решения.
для первого уравнения в (10), и, одновременно условием возможного существования автоволнового решения.
Вторая популяция движется на трофическом ресурсе ![]() меньшем, чем
меньшем, чем ![]() , который определяется как корень уравнения
, который определяется как корень уравнения
![]()
На рисунке при ![]() , отражено изменение функций
, отражено изменение функций ![]() на отрезке [0,1]. «Стрелками» отмечены направления движения автоволн. Решение уравнений (3) строилось в среде программирования математического пакета Matlab [9], использовалась встроенная функция pdepe с числом узловых точек равным 1500. Численные значения скоростей распространения популяций, поученные на «мелких» сетках, превышают теоретические значения на 2-4%.
на отрезке [0,1]. «Стрелками» отмечены направления движения автоволн. Решение уравнений (3) строилось в среде программирования математического пакета Matlab [9], использовалась встроенная функция pdepe с числом узловых точек равным 1500. Численные значения скоростей распространения популяций, поученные на «мелких» сетках, превышают теоретические значения на 2-4%.
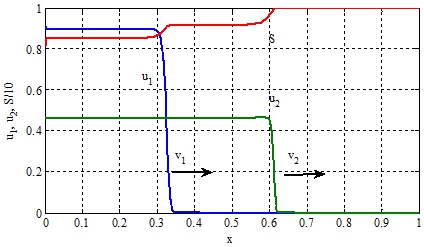
Рис. 1 – Графики зависимости функций ![]() , и в момент времени
, и в момент времени ![]()
Интерференционная конкуренция
В модели интерференционной конкуренции предполагается, что в отсутствие ресурса популяции не взаимодействуют между собой, а изменение их численности описывается логистическим уравнением. При больших объемах ресурса его количество не сказывается на взаимодействии популяций. С учетом этих предположений модель конкуренции двух популяций на неподвижном трофическом ресурсе записывается в форме системы трех нелинейных уравнений
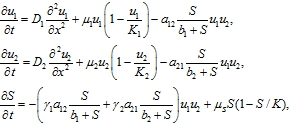 (11)
(11)
где ![]() ‑ число особей на единицу длины, параметры
‑ число особей на единицу длины, параметры ![]() n трактуются так же как и в эксплуатационной модели
n трактуются так же как и в эксплуатационной модели ![]() , ‑ положительные постоянные.
, ‑ положительные постоянные.
К системе уравнений (3) добавляются граничные условия (4) и начальные условия (5).
В локальной модели, следующей из (11) при ![]() , стационарное нетривиальное решение находится из системы трансцендентных уравнений
, стационарное нетривиальное решение находится из системы трансцендентных уравнений
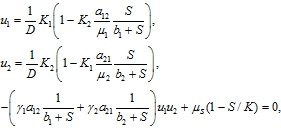 (12)
(12)
При ![]() из (11) следует модель двух независимых популяций. В неподвижной точке
из (11) следует модель двух независимых популяций. В неподвижной точке ![]() собственными значениями матрицы Якоби локальной модели будут
собственными значениями матрицы Якоби локальной модели будут
![]()
То есть при медленном восполнении трофического ресурса он постепенно будет исчерпан. Если неравенство (13) не выполняется, тогда правая часть третьего уравнения в (12) на промежутке ![]() будет менять знак. Соответственно это уравнение будет иметь нетривиальное решение
будет менять знак. Соответственно это уравнение будет иметь нетривиальное решение ![]() .
.
В неподвижной точке ![]()
![]()
Выполнение неравенства
![]()
обеспечивает устойчивость этой неподвижной точки.
То есть при медленном восполнении численности второй популяции или при большой емкости среды первой популяции вторая постепенно исчезнет.
Неподвижная точка
будет неустойчивой в силу положительности характеристических значений ![]() и матрицы Якоби. То есть при одновременном возникновении на трофическом ресурсе двух малочисленных популяций их численность начнет увеличиваться при незначительном влиянии конкурентного взаимодействия.
и матрицы Якоби. То есть при одновременном возникновении на трофическом ресурсе двух малочисленных популяций их численность начнет увеличиваться при незначительном влиянии конкурентного взаимодействия.
Возникновение конкуренции на появившемся ресурсе (при ![]() ) может сопровождаться его постепенным уничтожением (при выполнении неравенства (13)) и прекращением конкуренции, или его увеличением (при нарушение неравенства (13)) с продолжающейся конкуренцией или с подавлением одной из популяций другой за счет большой емкости собственной среды.
) может сопровождаться его постепенным уничтожением (при выполнении неравенства (13)) и прекращением конкуренции, или его увеличением (при нарушение неравенства (13)) с продолжающейся конкуренцией или с подавлением одной из популяций другой за счет большой емкости собственной среды.
При начальных условиях (5) первые два уравнения в (11) в линейном приближении приводятся к системе двух несвязанных уравнений
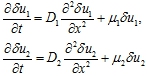
Отсюда следует, что у малочисленных популяций конкуренция является эффектом второго порядка малости. Распространение на отрезок в первом приближении для начальных условий (5) происходит с скоростями
![]()
Автоволновое решение
Автоволновое решение уравнений (11) представляется в виде функций одного аргумента ![]() , а искомые функции находятся их уравнений
, а искомые функции находятся их уравнений
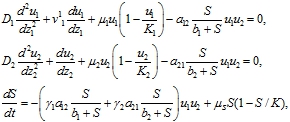
- При
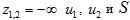 являются решением системы уравнений (12).
являются решением системы уравнений (12). - При
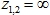
Первая стационарная точка в локальной модели устойчивая. Поэтому одно из собственных значений системы уравнений (14) будет отрицательным в этой точке. Соответственно в окрестности этой точки можно построить убывающее решение.
Распространение автоволн происходит с разными скоростями. Пусть ![]() . Тогда конкуренции в зоне опережения первой волной вторую нет. Скорость распространения первой волны будет
. Тогда конкуренции в зоне опережения первой волной вторую нет. Скорость распространения первой волны будет ![]() [6], [7].
[6], [7].
Поскольку вторая автоволна «догоняет» первую, то при ![]() для нее должны выполняться условия:
для нее должны выполняться условия: ![]() . Малое возмущение
. Малое возмущение ![]() при этих условиях должно удовлетворять линеаризованному второму уравнению в (14)
при этих условиях должно удовлетворять линеаризованному второму уравнению в (14)
![]()
и при условии, что ![]() , которое является условием неустойчивости положения равновесия с
, которое является условием неустойчивости положения равновесия с ![]() в локальной модели. Это условие допускает построение убывающего в точке
в локальной модели. Это условие допускает построение убывающего в точке ![]() решения.
решения.
На рисунке при ![]()
![]() , отражено изменение функций
, отражено изменение функций ![]() на отрезке
на отрезке ![]() . «Стрелками» отмечены направления движения автоволн. Решение уравнений (11) строилось в среде программирования математического пакета Matlab [9], использовалась встроенная функция pdepe с числом узловых точек равным 1500. Численные значения скоростей распространения популяций, поученные на «мелких» сетках, превышают теоретические значения на 5-10%.
. «Стрелками» отмечены направления движения автоволн. Решение уравнений (11) строилось в среде программирования математического пакета Matlab [9], использовалась встроенная функция pdepe с числом узловых точек равным 1500. Численные значения скоростей распространения популяций, поученные на «мелких» сетках, превышают теоретические значения на 5-10%.
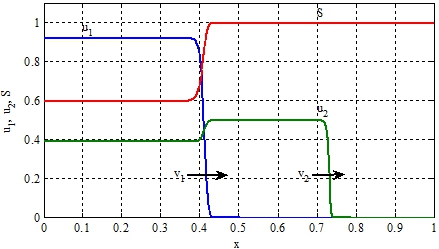
Рис. 2 – Графики зависимости функций ![]() , и в момент времени
, и в момент времени ![]()
![]()
Модель эксплуатационной конференции объясняет одновременное существование конкурирующих популяций на общем ресурсе. Наибольшая численность достигается у популяции с более высокой скоростью роста и с большим потреблением трофического ресурса. В модели Вольтерра одна из популяций должна погибнуть. Эти же условия позволяют одну из конкурирующих популяций опережать другую в освоении новых территорий. В модели интерференционной конкуренции возможны различные варианты: популяция, имеющая меньшую емкость среды, может погибнуть; при медленном восстановлении трофического ресурса он может быть исчерпан; обе популяции постоянно конкурируют на трофическом ресурсе.
| Благодарности Работа выполнена при поддержке гранта РФФИ мол_а № 18-31-00323. | Acknowledgement This work was supported by the RFBR grant mol_a No. 18-31-00323. |
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Вольтерра В. Математическая теория борьбы за существование / Вольтерра В.. Москва-Ижевск: Институт компьютерных исследований, 2004. – 288 с.
- Александров А.Ю. Математическое моделирование и исследование устойчивости биологических сообществ / А.Ю. Александров, А. В. Платонов, В. Н. Старков, Н. А. Степенко. – 2-е изд., испр. и доп. – СПб.: Издательство «Лань», 2016. – 272 с.
- Бигон М. Экология. Особи, популяции и сообщества: в двух томах / М. Бигон, Дж. Харпер, К. Таунсед. ‑ М.: Мир, 1989. Т. 1. – 667 с. Т. 2. – 477 с.
- Ghilarov A.M. In search of universal patterns in community organization: The concept of neutrality paved the way to a new approach / Ghilarov A.M. // Zhurnal Obshchei Biologii. – 2010. – V. 71. ‑ N 5. – PP. 386-401. PubMed: 21061639.
- Bazykin A.D. Nonlinear Dynamics of Interacting Populations. Singapure / Bazykin A.D., 1998. Сер. World Scientific Series on Non-Linear Science . 193 p. DOI: 10.1142/2284 ISBN 9789812798725.
- Колпак Е.П. Математические модели одиночной популяции / Е.П. Колпак, Е. А., Ефремова. – Казань: Изд-во «Бук», 2017. – 122 с.
- Murray J. D. Mathematical Biology / Murray J. D. New York: Springer-Vergal Heidelberg, 2002. – 776 p.
- Feng-Bin Wang A system of partial differential equations modeling the competition for two complementary resources in flowing habitats / Feng-Bin Wang // J. Differential Equations. – 2010. ‑ V. 249. – PP. 2866–2888.
- Колпак Е.П. Вычисления в MatLab: учебное пособие / Е.П. Колпак. – Казань: Изд-во «Бук», 2016. – 184 с.
Список литературы на английском / References in English
- Volterra V. Matematicheskaya teoriya bor'by za sushchestvovaniye [Mathematical Theory of Struggle for Existence] Moscow-Izhevsk: Institute of Computer Science, 2004. – 288 p. [In Russian]
- Alexandrov A. Yu. Matematicheskoye modelirovaniye i issledovaniye ustoychivosti biologicheskikh soobshchestv [Mathematical Modeling and Research of Biological Communities Stability] / A. Yu. Alexandrov, A. V. Platonov, V. N. Starkov, N. A. Stepenko. - 2nd, Corr. and added – SPb.: Lan publishing house, 2016. – 272 p. [In Russian]
- Bigon M., Harper J., Townsend K. [Ecology. Individuals, Populations and Communities: in Two Volumes] / M. Bigon, J. Harper, C. Townsed. M.: Mir, 1989. V. 1. – 667 p. V. 2. – 477 p. [In Russian]
- Ghilarov A.M. In search of universal patterns in community organization: The concept of neutrality paved the way to a new approach // Zhurnal Obshchei Biologii. – 2010. – V. 71. ‑ N 5. – PP. 386-401. PubMed: 21061639.
- Bazykin A.D. Nonlinear Dynamics of Interacting Populations. Singapure, 1998. Сер. World Scientific Series on Non-Linear Science . 193 p. DOI: 10.1142/2284 ISBN 9789812798725.
- Kolpak E. P. Matematicheskoye modelirovaniye i issledovaniye ustoychivosti biologicheskikh soobshchestv [Mathematical Models of Single Population] / E. P. Kolpak, E. A., Efremova. – Kazan: Publishing house "Beech", 2017. – 122 p. [In Russian]
- Murray J. D. Mathematical Biology. New York: Springer-Vergal Heidelberg, 2002. – 776 p.
- Feng-Bin Wang A system of partial differential equations modeling the competition for two complementary resources in flowing habitats / Feng-Bin Wang // J. Differential Equations. – 2010. ‑ V. 249. – PP. 2866–2888.
- Kolpak E.P. Vychisleniya v MatLab: uchebnoye posobiye [Calculations in MatLab: Study Guide] / E.P. Kolpak. – Kazan: Publishing house "Buk", 2016. - 184 p. [In Russian]
